基本不变量神经网络解析梯度方法的研究

2021-07-11 16:14商辰尧张东辉

高等学校化学学报 2021年7期

商辰尧，张东辉

（1.中国科学院大连化学物理研究所,分子反应动力学国家重点实验室,大连116023；2.中国科学院大学,北京100049）

多原子体系的势能面构建是理论化学研究中的一个重要课题［1～4］.根据波恩-奥本海默近似，分子体系的薛定谔方程可以近似拆分为原子核薛定谔方程与电子薛定谔方程.由于电子质量远小于原子核质量，在求解电子薛定谔方程时，可以近似认为原子核位置不变，由此可以求解出给定原子核坐标下的电子势能.以原子核坐标为自变量的电子势能函数即为势能面.通过采用高精度的从头算方法，如多参考组态相互作用（MRCI）方法或耦合簇（CC）方法，再结合函数插值或拟合等方法，就可以构造出高精度的势能面.构造完成之后的势能面可以用于进行一系列的化学动力学计算，如基于量子力学的量子动力学计算、以及基于牛顿力学的准经典轨线计算.利用精确的动力学方法，可以求解分子振转光谱、化学反应速率常数、以及态-态反应微分截面等信息.随着计算机性能的提升，人们开始追求更为准确的动力学模拟结果.高精度势能面不再仅被应用于小分子体系的计算中，而逐渐开始被应用于如分子动力学模拟这种研究体系宏观热力学性质的领域［5～7］.

在实际的动力学模拟过程中，体系往往存在一些全同原子，交换两个相同原子的坐标后，势能面的输出值不发生改变，这就是势能面的置换不变性.全同原子置换不变性是势能面构造时必须要解决的一个问题.解决置换不变性最简单的方法是将原子序号按照某种给定的规则进行排序［8］，这种排序规则通常以原子间距离为依据.通过排序，分子坐标被映射到一个唯一的子空间，对这个子空间中的分子构型进行拟合，即可以得到具有置换不变性的势能面.然而，这种方案并没有从根本上解决势能面函数置换不变的问题，仅是通过排序避免了原子坐标发生置换的可能性.对于具有较高对称性的体系，坐标空间中往往存在多个对称面.由于拟合时仅仅考虑由对称面包围的唯一一个子空间，函数在对称面处的一阶导数往往是不连续的.对于基于牛顿力学的动力学方法——如准经典轨线方法，这种不连续将导致原子在对称面处的受力发生突变，从而导致错误的动力学结果.为了解决多原子体系中全同原子置换不变性问题，Bowman等［9～11］发展了置换不变多项式（PIP）方法.置换不变多项式是指在原子交换操作下数值不发生改变的一组多项式.置换不变多项式可以通过启发式方法——如单项式对称化方法（MSA）生成，也可以借助数学中的不变量理论，通过求解首要不变量和次要不变量系统地生成.在PIP方法中，势能面被构造为置换不变多项式的线性函数，在产生体系的置换不变多项式之后，通过最小二乘法拟合体系的势能，进而得到具有置换不变性的势能面.Guo等［12～15］在PIP的基础上，更进一步将置换不变多项式作为神经网络的输入，发展出了PIP-NN势能面.在构造PIP获得置换不变性的基础上，利用神经网络的强大函数拟合能力，可以精确地构造更为复杂体系的势能面.另一方面，Behler等［16～19］发展了高维神经网络（HDNN）方法.该方法基于以下假设：体系的电子势能只与相距较近的原子间产生的相互作用有关.在这条假设下，体系的总势能可以表示为每个原子贡献的局部势能之和，即式中每个原子的势能只与该原子附近的化学环境相关.Behler等［17］设计了一组具有平移、转动、置换不变性的对称函数，用于描述给定原子周围的化学环境.在计算每个原子的化学环境之后，将对称函数作为神经网络的输入，从而得到每个原子的局部势能，最终通过对局部势能求和，得到整个体系的总势能.

在保证势能面精度的情况下，势能面的计算速度会直接影响动力学模拟的效率.尽量减小势能面模型的大小，提高计算速度，是研究人员一直以来的努力方向.尽管PIP方法能够解决置换不变性问题，但是随着体系的增大，多项式的项数会急剧增长，将全部的多项式用于拟合势能面会导致势能面的计算成本过于庞大.为了控制势能面的计算规模，通常的办法是按照多项式的最高次数对多项式进行截断，从而控制多项式的总数目.然而，这种对PIP项数的限制方法具有一定的随意性.在进行截断前，无法预先知道哪部分多项式对势能面的拟合更有帮助，而哪部分的多项式实际上存在冗余，应当被除去.为此，Shao等［20］和Chen等［21］从基本不变量理论出发，发展了基本不变量神经网络（FI-NN）方法，以数学理论为依据减少了置换不变多项式的项数.如前所述，置换不变多项式可以通过计算首要不变量与次要不变量来生成.事实上，次要不变量可以进一步分解为可约次要不变量与不可约次要不变量，其中不可约次要不变量可以作为可约次要不变量的生成元.这就意味着，置换不变多项式环的生成元存在一个最小集合，这个集合是首要不变量和不可约次要不变量的子集，也就是所谓的基本不变量（FI）.依据计算不变量理论以及King等［22］提出的算法，基本不变量可以通过程序直接生成.将生成后的基本不变量作为神经网络的输入，就可以构造出FI-NN势能面.相对于启发式地构建置换不变多项式，基于基本不变量的多项式天然具有项数更少的优点，并且在数学上保证了这种项数的减少不会影响多项式对构型空间的表达能力.

除了减小势能面模型的规模之外，直接在势能面调用步骤上进行优化，也能够提高势能面的调用速度.在以经典力学为基础的动力学模拟——如准经典轨线方法和分子动力学模拟方法中，计算每个原子受到的相互作用力往往是整个模拟的决速步骤.在保守力系统中，原子间的相互作用力等于原子间势能对坐标偏导的负数，可以通过求解势能面对笛卡尔坐标的偏导得到.由于势能面的函数形式往往十分复杂，对于简单体系，势能面对坐标的偏导数可以简单采用数值差分的方法近似得到.考虑到势能在笛卡尔坐标向量x中第i个分量的偏导数，根据多元函数微分原理，可以近似地将该偏导数用数值方法求解为

式中：E为势能面的输出能量；x代表体系的笛卡尔坐标向量，其由体系内每个原子的笛卡尔坐标拼接而成，其维度为3×原子数；x i代表笛卡尔坐标向量的第i个分量；Δx是数值微分时的距离间隔，通常是一个任意设置的、足够小的正实数.

由上式可见，势能面梯度的数值解法具有求解简单的优点.只要能够得到势能面的能量值，就可以轻易地得到势能面梯度的近似解.然而同样可以注意到，该方法在求解时，需要对体系内每一个原子的每一个维度调用2次势能面，对于一个有N个原子的系统来说，求解一次数值梯度需要进行6N次势能面的调用.随着体系规模N的增大，这种调用带来的成本也会成比例的增大.更为严重的是，随着体系原子数目的增加，势能面所描述的构型空间显著增大.为了维持较高的势能面精度，研究者往往需要使用更大规模的神经网络，这就意味着体系规模的增大使单次调用势能面的成本也相应增加.显然，在上述两种因素的叠加影响下，简单采用数值方法来求解体系的能量梯度已经无法满足更大体系的动力学研究.因此，需要寻求更为高效的势能面梯度求解方法.

事实上，由于在某一特定体系下，势能面往往具有静态的数学形式，可以预先求解出势能面对笛卡尔坐标偏导的解析解.将势能面的求解算法和势能面梯度的解析公式一起作为编译期确定的函数，在调用前预先编译成机器指令，可以极大地提高势能面梯度的求解效率.通过解析方法求解势能面只需调用一次解析梯度版本的势能面函数，函数的调用次数不再随原子数N线性增加.尽管解析梯度势能面函数的单次调用时间会有所增加，但是在总体上依然能提高势能梯度的求解效率.

本文发展了基于FI-NN的解析梯度势能面方法.通过求解FI-NN势能面函数的解析导数，精确求解了势能面的梯度，同时极大地提升了势能面的调用速度.

1 理论方法

1.1 FI-NN算法

首先，简要介绍一下FI-NN势能面的计算流程，然后再对势能面的解析梯度算法进行推导.

在进行动力学模拟时，通常采用笛卡尔坐标系来描述体系中原子的坐标，由于笛卡尔坐标不具备平移、转动、置换不变性，首先将笛卡尔坐标转换成内坐标：

式中：r ij表示原子i与原子j之间的距离；x i和x j分别表示原子i与原子j的笛卡尔坐标.

通过计算每两个原子间的距离，可以构建内坐标向量r.对于有N个原子的体系，内坐标向量的维度为N×(N-1)/2.构建好内坐标之后，体系描述只剩下置换不变性需要解决，可以用FI多项式来解决这个问题，但是在此之前，一般会先将内坐标变换成倒数或e指数形式.研究发现，如果将原子间核间距变换为类似于Morse力场形式，在势能面拟合中往往会取得更好的拟合结果［9］，这可能是由于Morse形式本身已经是分子间作用力的一种较为粗略的近似.类似地，将内坐标变换为倒数形式也能起到与Morse型变换类似的拟合提升效果.将变换后的向量表示为y：

式中：r是内坐标向量；λ是一个与体系有关的常数，用于控制衰减系数.随后，将向量y变换为具有置换不变性的FI多项式p：

式中：生成FI多项式的过程由算符F^表示，具体的实现步骤可以参考Shao等［20］和Chen等［21］的研究结果.至此，已经得到了具有平移、转动和置换不变性的分子构型描述方式.

这里需要注意的是，在训练神经网络时，通常会将由训练集计算出的FI多项式和从头算的能量进行归一化处理，使得神经网络的输入数据和目标输出均介于[-1，1]之间.这样确保了神经网络的输入输出的数值不会过大，使神经网络能有更好的拟合效果.

式中：a0为真正输入到神经网络的输入层数据；t为神经网络拟合时的待学习数据；p是由数据集中的某个构型计算得到的FI多项式；pmin和pmax是与p相同维度的向量，分别代表p向量在数据集中每个维度能取到的最小值和最大值；E是由从头算方法得到的体系势能；Emin和Emax分别是数据集中所有从头算能量的最小值和最大值.

与深度学习领域常选用深层神经网络不同的是，在势能面构建时，通常只选用简单的双隐层前馈型神经网络.一方面，双隐层的神经网络已经足以用于表达任何复杂函数形式，因此这种神经网络结构已经足够用于势能面的构建.另一方面，动力学计算的速度严重依赖于神经网络的运算速度，在保证足够精度的情况下，会尽可能选用计算效率最高的机器学习模型.神经网络的计算公式如下：

式中：下角标代表变量所在的神经网络层数：下角标0代表输入层，下角标1，2代表第1，2层隐藏层，下角标3代表输出层；向量a代表神经网络的神经元数据；向量z代表神经网络前向传播过程中，线性变换部分的计算结果；矩阵W i是连接第（i-1）层和第i层的权重矩阵，设第（i-1）层有m个神经元，第i层有n个神经元，那么矩阵W i的维度为(n×m)；向量b i为偏置向量，维度为n.在这里，输出层的数据较为特殊；由于神经网络的输出层只经过线性变换，因此z3就是神经网络的输出数据，又由于输出数据z3为标量，因此，矩阵W3实际上是一个行向量，偏置值b3是一个标量.函数f(z)为神经网络的激活函数，这个函数用于对神经元间传递的数据做一个非线性变换.常用的激活函数为sigmoid函数和tanh函数.在这里为了提升势能面的调用速度，采用作为激活函数，这个函数由于不需要进行指数计算，在具有较高拟合精度的同时，调用速度稍快于上述2个函数.由于在训练神经网络时，对神经网络的待学习数据进行了归一化处理.因此，在需要实际调用神经网络势能面时，需要对神经网络的输出进行逆变换，以得到势能面的输出能量：

以上就是从笛卡尔坐标系下的分子坐标得到分子构型能量的完整步骤.

1.2 FI-NN解析梯度算法

现在开始求解势能面在笛卡尔坐标下的解析梯度.要得到的目标变量是能量对笛卡尔坐标的导数dE/dx.根据链式求导法则可以得出：

式中：E为势能面的输出能量；x为笛卡尔坐标向量；其余变量的含义均与上文一致.任意两个向量间的导数以雅克比矩阵方式排列：

式中：向量a与向量b是任意两个向量.

根据该定义［式（13）］，dE/dx是一个行向量，维度为3×原子数.公式中第一项dE/dp可以使用神经网络中的反向传播算法计算：

式中:diag[a]的作用是将向量a转化成对角矩阵,其中a是任意一个向量:

式（13）中dp/dy即为对FI多项式的求导.不同的势能面所采用的FI多项式的形式可能各不相同，因此无法像推导神经网络反向传播公式那样得到一个统一的解析解.但是，FI的函数形式至少在编译期是确定的，因此可以编写一个自动计算FI解析梯度的程序.该程序以FI的多项式公式作为输入，然后将FI的解析梯度输出成一个编译期确定的函数.以一个AB3体系为例，体系中共有4个原子，因此总的内坐标个数为6个.通过基本不变量生成方法，可以将内坐标转化为共有9项的基本不变量多项式.本文只截取前5项为例：

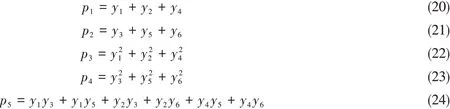
通过自动微分程序，可以将上述多项式的微分输出为

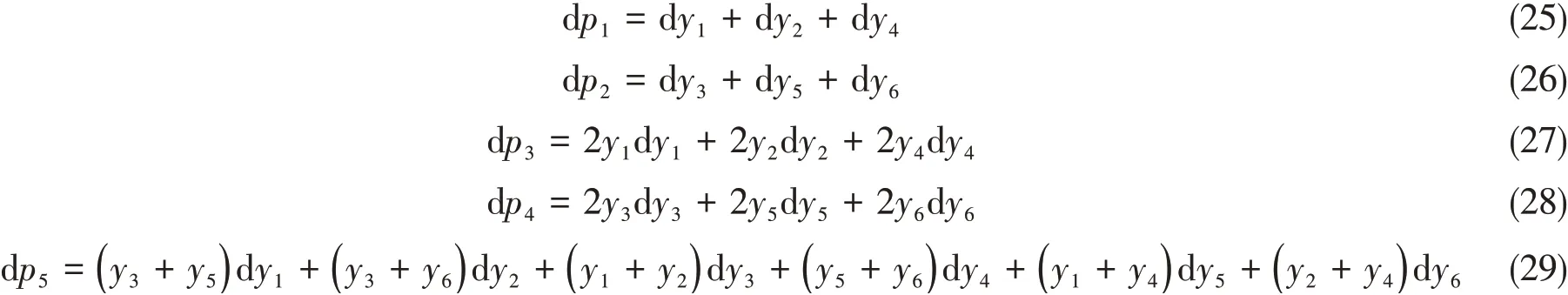
最后来求解dy/dx，在这里仅考虑y=1/r的情况，对于y=exp(-r/λ)的情况用类似的方法不难得到.考虑向量y的第k个分量y k：

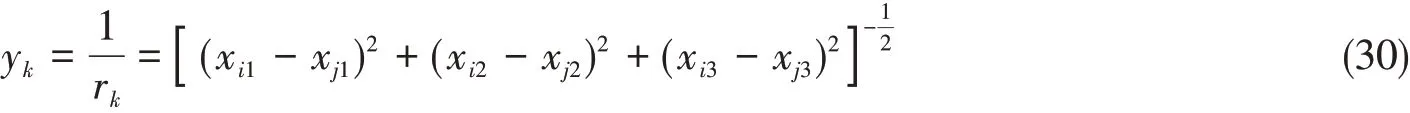
式中：r k是内坐标向量r的第k个分量；x i1代表第i个原子的笛卡尔坐标在x轴方向上的分量，其余变量的含义与之类似.

利用求导法则不难得出：

在对一个N原子体系的内坐标求解时，i和j的遍历满足1≤i＜j≤N，在这种情况下，i，j和k存在如下关系：

根据式（31）和（32）就可以求解dy/dx矩阵中的每一个元素.需要补充的是，在算法的具体实现中存在一些优化的办法.尽管可以根据上述公式编写一个二重循环逐次地求解dy/dx矩阵中的每一个元素，然而可以注意到，上述求解公式在编译期同样是确定的.因此，依然可以编写一个程序，自动生成矩阵的求解代码.这样，i，j和k的数值在编译期就能确定下来，从而避免了每一步必须动态求解的时间成本.

2 结果与讨论

选用水分子的多体相互作用势能面来对解析梯度方法进行测试.对于一个由N个水分子构成的团簇，体系总势能可以分解为若干多体相互作用能的叠加［23-26］：

式中：E N表示N个分子的总势能；VNB表示N体相互作用能；x i代表第i个水分子的笛卡尔坐标.根据上述方法，构造了水分子的两体、三体、四体势能面.其中两体势能面采用UCCSD（T）/CBS方法进行从头算［27］，三体、四体由于体系较大，采用双杂化泛函XYGJ-OS/AVTZ进行从头算［28］.研究表明，大于四体的水分子相互作用影响十分有限，因此并没有构造更高阶的相互作用势能面［29］.由式（34）可以看出，N体相互作用势能面需要使用所有N个水分子的笛卡尔坐标，势能面的规模势必会随着N值相应增大.另一方面，在计算N体相互作用能的贡献时，需要遍历所有由N个水分子构成的组合，当体系的分子数较多时，这样的组合数就会十分庞大.由于上述2个原因，降低多体相互作用势能面的计算成本变得十分重要，这就是为什么用这一组势能面来验证解析梯度方法的效果.

下面来验证上述解析梯度方法的正确性.由于数值梯度的求解十分简单，能够用数值方法几乎无误地得到一个势能面梯度的近似值.如果解析梯度的结果与数值结果十分接近，就可以认为采用的解析梯度方法是正确的.另一方面，当确认上述推导的解析梯度算法有效之后，可以用解析梯度的结果反过来评判数值梯度的结果.根据前面所述，数值梯度是通过给笛卡尔坐标变动一个较小的位移Δx来近似求得能量梯度，然而这个Δx的最优数值无法预先知道.理论上，Δx越小所得到的结果越接近于真实值，但由于计算机在处理浮点数时存在精度问题，过小的Δx会使最终的结果不稳定.同样的，如果选用的Δx过大，在能量变化十分剧烈的位置求得的数值梯度可能会与该位置的真实梯度产生较大偏差.通过对比数值梯度与解析梯度的结果就可以看出所选用的Δx是否合适.

图1示出了在111772个两体水分子构型上分别使用数值梯度和解析梯度计算得到的O原子受力（Fanal.-Fnum.）的差值.可以看出，绝大部分的差值在10-4eV/nm以下，考虑到在两体水分子相互作用能中，O原子受力的绝对值通常在±100 eV/nm范围内，解析梯度与数值梯度之间的误差小于十万分之一，可以认为上述解析梯度算法已经得到了正确的结果.从图中可以看到，O原子之间的距离（ROO）越近，解析梯度与数值梯度的差值就越大.这是因为当两个分子逐渐接近时，分子间的相互作用越强，势能面的变化越剧烈，在Δx不变的情况下，数值梯度引入的误差就越明显.

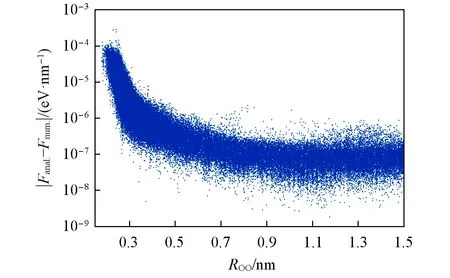
Fig.1 Errors between numerical and analytical gradient on two-body water structures

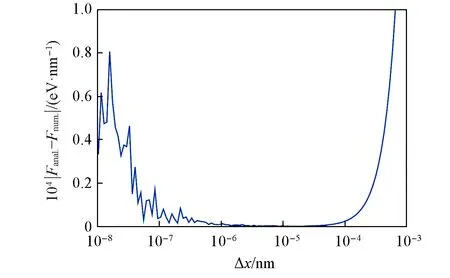
Fig.2 Errors between numerical and analytical gradient on different choices ofΔx

图2示出了在两个水分子的平衡构型上，数值梯度与解析梯度在O原子上的差值随数值梯度中Δx的变化趋势.可见，10-5nm附近是Δx的最佳取值范围，当Δx值大于10-4nm后，数值梯度引入的误差开始急剧增大，当Δx值小于10-6nm后，由计算机浮点数引入的不稳定性开始逐渐明显起来.总体而言，在水的平衡构型处，当选择了较为合适的Δx时，数值梯度与解析梯度的误差处于10-5eV/nm的数量级内，属于可以接受的范围.但同时需要指出的是，相比于最佳的Δx取值，随意地选择一个不合适的Δx可能会导致数十倍的误差.因此，在单纯使用数值梯度势能面的场合下，有必要事先对Δx进行扫描，从而寻找一个合适的取值.

解析梯度势能面方法最重要的意义在于提高势能面的调用速度.为此，对势能面的运行时间进行了测量.由于测量的目的仅在于对比解析梯度与数值梯度的速度差异，测试程序的绝对运行时间可以根据需要进行调节.在测量时，如果程序运行时间过短，测得的数据就不够准确.反之，如果运行时间过长，则没有必要.为了能够方便地调节测试程序的运行时间，预先将待测试的分子构型加载到一个数组中，再选定一个合适的迭代次数，对数组中的分子构型进行势能面调用.这样，程序的运行时间与自行设定的迭代次数相关，可以任意调节.为了避免计算机缓存带来的运行速度干扰，并没有按数组顺序依次进行遍历，而是每次生成一个随机数，随机地挑选数据集中的某个分子构型进行势能面读取.由于势能面的运行速度与参与计算的数据值无关，这种随机挑选构型的方法是合理的.

表1示出了在多个水分子多体相互作用势能面上分别进行势能计算和势能梯度计算所用的时间.对于两体势能面，选用了具有66621个两体水分子构型的数据集，每次测试进行了107次迭代.除此之外，分别测试了多个具有不同结构的三体、四体势能面.其中，所有三体势能面的测试均采用了139929个三体水分子的数据集，每次测试进行了106次迭代；所有四体势能面的测试均采用了152490个四体水分子的数据集，每次测试进行了105次迭代.在这种安排下，由于三体、四体势能面没有选择相同的迭代次数，二者的绝对运行时间没有可比性，但是同属于三体或四体的不同势能面之间具有比较价值.由此可以看出不同势能面结构对势能面运行速度的影响.

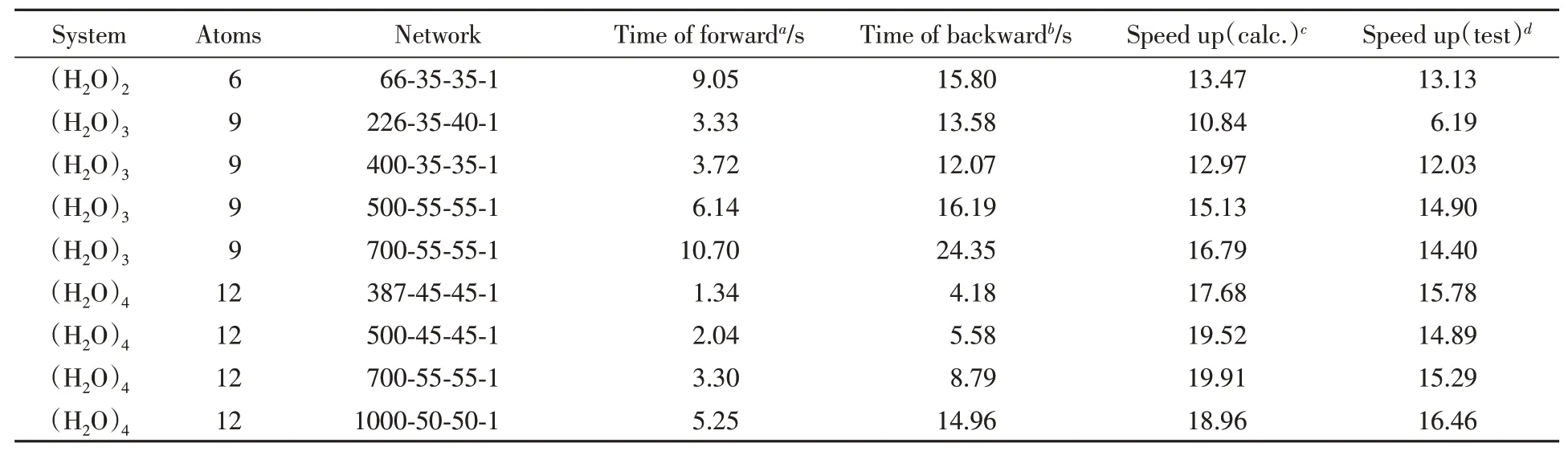
Table 1 Comparison of calculation time of forward and backward propagation on FI-NN PESs

表1的第一列表示势能面描述的体系，分别是两体、三体和四体相互作用能.第三列示出了势能面采用的神经网络结构.对于三体和四体势能面，为了得到较高的拟合精度，分别选用了不同的神经网络结构进行拟合.显然，神经网络规模越大，势能面计算成本也会越大.神经网络第一层的大小既表示神经网络的输入层维度，也代表基本不变量的项数.表中第四、五列示出了势能面前向传播与反向传播的计算时间.前向传播是指从分子笛卡尔坐标计算得到分子势能所用的时间，反向传播指求解势能梯度所用时间.由图2可见，反向传播过程的耗时往往数倍于前向传播，这是因为在反向传播中需要计算多个向量间的雅克比矩阵.根据上述两个时间，可以在理论上估算解析梯度方法带来的加速效果.考虑一个N原子体系的势能面，如果需要得到该体系的总势能和势能梯度，设势能面的前向传播耗时为t1，反向传播耗时t2，采用解析方法计算梯度的加速比可以按如下公式计算：

表1中第六列示出了式（35）的计算结果，第七列示出了实际势能面调用时的加速比.注意到二者数值并不完全相同.这是因为，为了测试势能面的前向传播与反向传播，势能面程序需要进行一些结构上的调整，并在计算过程中插入计时函数，这些操作一定程度上都会影响势能面的调用速度.但是可以看到，两列数据具有大致相同的变化趋势.由表1可见，尽管反向传播的计算成本较高，相比于数值方法，采用解析方法计算势能面梯度依然能带来10倍以上的性能提升.并且，相同体系的势能面采用的FI项数越多，解析梯度方法带来的性能提升也就越大.在处理较大体系时，为了保证势能面拟合的精度，往往需要增加FI项数.因此，随着研究体系的增大，采用解析梯度方法能够带来更加明显的性能收益.

3 结论