轮毂驱动电动车辆动力学稳定性滑模控制策略研究*
王伟达 † 张宇航 黄国强 1 孙晓霞 3 杨超 1 马正
(1.北京理工大学机械与车辆学院,北京 100081)(2.北京理工大学重庆创新中心,重庆 401122)
(3.中国北方车辆研究所,北京 100072)
引言
近年来,随着我国能源产业升级,新能源汽车在整个汽车行业中所占比重逐年增大.纯电动汽车、燃料电池汽车和混合动力汽车均受到了社会各界的广泛关注[1].其中,轮毂驱动电动车辆因其节能环保、机械结构简单、驱动系统效率高及整车质量轻等优势,成为纯电动汽车发展的重点.而轮毂驱动电动车辆因为在行驶时需要对其四个轮毂电机的转速转矩进行独立控制,其控制系统自由度更多,更加复杂,控制系统对于车辆的动力学稳定性的影响也更显著,进而影响了车辆的安全性[2,3].因此研究轮毂驱动电动车辆的动力学稳定性控制策略具有重要意义.
近年来在轮毂驱动电动车辆稳定性控制方面,一些国内外学者进行了相关研究,并取得了一定成果.在国外,Farzad Tahami等[4]人设计了基于模糊逻辑直接横摆力矩控制的轮毂驱动电动车辆控制器;Avesta Goodarzi等[5]人基于横摆角和车身滑移角的成本函数,设计了一种多层车辆稳定性控制器;而Hasan Alipour等[6]人在路面湿滑的特殊条件下设计了基于滑模控制原理的车辆横向稳定性控制器,并进行了Carsim/Matlab的联合仿真验证;在文献[7]中,Asal Nahidi等人应用了模型预测控制的方法模块化地解决了车辆纵向和横向稳定性综合控制的问题.在国内,文献[8]提出了一种基于动态单纯形算法的车辆状态最优观测器,能够实时监控质心侧偏角、路面附着系数等车辆关键状态,提高了已有车辆稳定性控制器的精度和控制效果;同济大学的余卓平等[9]人采用层次化结构的控制分配方法来提高车辆的操纵稳定性;清华大学的曹坤等[10]人针对分层式轮胎纵-横-垂向力协同优化控制系统中的优化分配部分,建立了统一优化目标函数,解决了轮毂驱动电动车辆的协同优化控制难题;吉林大学的张缓缓[11]基于BP神经网络的PID控制方法联合控制横摆角速度控制,进行了车辆的转矩分配,并同样采用了层次化的控制器设计方法;而湖南大学的黄彩霞等[12]人同样基于双层控制架构,提出了基于区域极点配置的轮毂驱动电动车辆横向稳定性控制策略,最大限度地利用了路面附着能力,对轮胎侧偏刚度等参数不确定性具有较强的鲁棒性.综上所述,众多学者针对轮毂驱动电动车辆的稳定性控制问题已经进行了广泛且深入的研究,但在控制参数的选择上,现有工作通常使用相同的控制参数应对车辆行驶条件的变化,如在不同的路面附着系数与车速下,均采用质心侧偏角作为控制参数.然而在不同工况下,不同控制参数的控制效果不同.若只选用固定的控制参数进行控制,则会造成控制效率的降低,甚至对控制效果产生极大影响.因此,需要针对车辆的不同工况对控制参数进行调整,但目前基于不同控制参数的控制效果进行比较和选择优化的研究还有所欠缺.
本文将对车辆失稳原因进行综合分析,并提出基于质心侧偏角和横摆角速度的滑模变结构直接横摆力矩控制策略,设计双层控制器,并在所搭建的Carsim/Simulink联合仿真平台中设计不同工况,对两种基于不同控制参数的控制策略的有效性和鲁棒性进行比较探究.
1 车辆操纵稳定性表征
1.1 横摆角速度与车辆稳定性的关系
根据车辆动力学,车辆的运动状态可以用其质心侧偏角和横摆角速度来描述.在车辆动力学模型中,其质心侧偏角可以通过车辆的纵向速度和侧向速度来确定.而车辆的航向角ψ则可由下式表示:

式中,β为质心侧偏角;γ为横摆角速度,其积分为车辆的横摆角.车辆的横摆角速度γ在侧偏角β很小的情况下所表征的是车辆的转弯能力,即横摆角速度越小,车辆的转弯半径越大,转弯越慢;反之,车辆的转弯半径越小,转弯越快.
由于车辆的转向特性是影响车辆稳定性的关键因素,下面将通过车辆横摆角速度与转向特性的关系,分析它与车辆稳定性的关系.车辆的转向特性一般由前、后轴侧偏角的绝对值之差来确定,如式(2)所示:

式中,αf,αr分别为前后轴侧偏角,其值可分别由式(3)、(4)求得:

其中,δ为车辆转向角,u是纵向速度,v是侧向速度,lf,lr分别为质心到前轴和后轴的水平距离.所以车辆的转向特性也可由下式表示:

式中,l为车辆轴距.由式(3)和式(5)可知:

因此,当质心侧偏角一直保持在比较小的范围(±5°)内时,可以通过横摆角速度来判断车辆的转向特性,进而分析车辆是否失稳.即在此情况下,横摆角速度与方向盘转角的增益可以表征车辆的稳定性.但是当车辆发生甩尾等严重的侧滑现象时,质心侧偏角较大,横摆角速度就不能够完全表征车辆稳定性,此时需要对车辆稳定性进行进一步分析.
1.2 质心侧偏角与车辆稳定性的关系
一般来说,能否用横摆角速度完全表征车辆稳定性,与转向时轮胎侧偏角的大小有直接关系:若轮胎侧偏角比较小,轮胎处于线性区域,这时驾驶员可以通过对方向盘的操作使车辆达到期望的行驶轨迹,即可以用横摆角速度表征车辆的稳定性;若轮胎侧偏角比较大,轮胎进入非线性区域,这时的横向运动也是非线性的,横摆角速度就无法完全描述当前的车辆横向稳定性状态,此时需采用质心侧偏角来衡量车辆的稳定性.质心侧偏角对车辆横摆运动的影响如图1、图2所示(μ为轮胎附着系数).

图1 质心侧偏角对横摆力矩和总侧向力的影响(u=100km/h,μ=1.0,γ=0)Fig.1 Effect of sideslip angle on yaw moment and total lateral force when u=100km/h,μ=1.0,γ=0
从图2中可以看出,车辆的横摆力矩与侧向力的增加量是随着汽车前轮转角δ的增大而减少,即随着侧偏角的增大,轮胎逐渐由线性区域进入饱和区域.从图1可以看出,当车辆质心侧偏角接近零时,汽车产生的横摆力矩与汽车前轮转角有着相同的方向,轮胎的纵向力有很大裕度,此时车辆处于比较稳定的状态.在当前轮转角持续增大时,总侧向力的增加量减小,轮胎开始进入饱和区域.

图2质心侧偏角对横摆力矩和总侧向力的影响(u=100km/h,μ=0.2,γ=0)Fig.2 Effect of sideslip angleon yaw moment and total lateral force when u=100km/h,μ=0.2,γ=0
随着质心侧偏角增大,横摆力矩增大到峰值后开始减小,此时车辆的状态很容易受到外界的干扰而产生变化.当质心侧偏角持续增大至产生的横摆力矩为零时,驾驶员不能再通过操纵方向盘来改变汽车产生的横摆力矩了,即此时已经无法通过人为操纵转向系统使车辆恢复到稳定状态了.
图2描述的是低附着系数路面(μ=0.2)的仿真曲线,可以看出图2与图1有着类似的变化规律.不同的是在低附着路面上车辆的横摆力矩趋近于零的速度更快,轮胎纵向力趋近于饱和状态的速度也更快,即车辆更容易进入不稳定的状态.通过以上分析,在行驶过程中车辆质心侧偏角的变化对车辆的稳定性的影响非常大,尤其在低附着系数的路面上这种影响更加明显.
1.3 车辆稳定性判据



表1 横摆角速度偏差失稳区临界值Table 1 Critical values of the yaw rate deviation instability area

表2 相平面稳定性边界参数Table 2 The phase-planestability boundary parameter

式中B1,B2为稳定性边界常数.图3为车速是60 km/h、路面附着系数μ=0.85、前轮转角为0 deg的车辆相平面图.

图3 相平面(δ=0deg,μ=0.85)Fig.3 Phase plane(δ=0deg,μ=0.85)
2 动力学控制策略
本文采用的控制策略为直接横摆力矩控制,其基本思想是通过改变车辆内、外侧车轮上的纵向力,产生附加的恢复横摆力矩来改善车辆稳定性,提高极限工况下车辆的转向能力.该方法能显著地改善非线性车辆在变速转向时的稳定性.
在转向过程中,车辆的横摆力矩与车轮所受的纵向力和侧向力有关.在忽略车轮所受滚动阻力的情况下,轮胎的纵向力和侧向力是相互耦合的,其满足如图4所示的摩擦椭圆关系.这种关系可以表示为式(9)所示的形式.当轮胎的纵向力增大时,地面能提供给轮胎的最大侧向力必然减小,因此,纵向力的变化会伴随着侧向力的变化.由于在控制过程中,轮胎侧向力是不可控变量,因此本文主要考虑控制纵向力的变化对车辆转向稳定性的影响.

图4 轮胎摩擦椭圆Fig.4 Tirefriction ellipse

式中,Fx,Fy分别为轮胎所受实际纵向力和侧向力;Fxmax,Fymax分别为地面所能提供的最大纵向力和最大侧向力.
2.1 控制策略双层架构
本文主要根据轮毂驱动电动车辆可以对每个车轮的驱动力矩进行独立控制的特点,设计了动力学稳定性控制策略.控制策略采用了层次化结构,其控制架构如图5所示.所设计的上层控制器为车辆运动控制器,通过车辆线性二自由度动力学模型[15],根据当前车辆的运动状态,设计理想的目标质心侧偏角和横摆角速度,然后由基于滑模变结构的控制算法计算出能够让车辆跟随理想侧偏角和横摆角速度的附加横摆力矩.下层控制器为车轮力矩分配控制器,其功能是将上层控制器计算的期望横摆力矩通过在满足各执行器约束边界的情况下,基于轮胎利用率最小的控制算法,最优分配出四个轮毂电机的目标力矩,以保证质心侧偏角和横摆角速度在安全行驶的区间内,从而达到提高车辆稳定性的目的.

图5 驱动控制策略示意图Fig.5 Schematic diagramof drivecontrol strategy
图5中,Vd,δ分别是驾驶员预期的车辆行驶速度与前轮转向角;预期车辆横摆角速度γd和质心侧偏角βd分别利用预期速度与转向角进行解算,其参数曲线只受速度与参考轨迹影响;γ,β是此时车辆实际的横摆角速度和质心侧偏角;Mz为上层控制器解算出的附加横摆控制力矩;Ti(i=1,2,3,4)则是由下层控制器基于轮胎利用率最小的最优控制算法计算出的各驱动轮转矩.
该上层控制器的工作流程是:驾驶员模型根据设定的工况给与期望的车辆行驶参数,该期望的车辆行驶参数与当前车辆的状态参数一并输入给上层控制器.上层控制器通过计算得出期望的附加横摆控制力矩,输入给下层控制器,下层控制器求解出四个电机的目标转矩,并反馈给车辆,从而保证了车辆在行驶过程中的动力性和稳定性.
2.2 滑模变结构控制原理
滑模变结构控制是属于变结构控制系统中的一种控制方法.其基本思想是将原有控制信号(zz)替换为sgn(z-z),以改善原有控制信号的不连续性.该策略具有一种使系统“结构”随时间变化的特性,该控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动.这种滑动模态与系统的参数及扰动无关,处于滑动运动的系统具有很好的鲁棒性.滑模变结构控制的基本原理如下:
设有非线性控制系统

存在切换函数s(x),s∈Rm,将原有控制信号u转化为式(11)所示形式.

在这个控制模型中,必须满足以下三个条件才能保证受控系统全局渐近稳定,且动态品质良好:
(1)滑动模态存在,即式(11)成立;
(2)满足到达条件:切换面s=0以外的相轨迹线将于有限的时间内到达切换面,即满足式(12);
(3)切换面是滑动模态区,且保证滑动运动渐进稳定,即满足式(13).

2.3 基于滑模变结构控制的上层控制器设计
车辆上层控制器将汽车行驶过程中的质心侧偏角和横摆角速度作为车辆稳定性控制系统的反馈控制状态参数,利用滑模变结构控制理论来决策出上层控制器需要输入给下层控制分配器的期望横摆力矩.一般认为,在高附着路面情况下,应以横摆角速度作为主要的控制量,而在低附着路面和大侧偏角的情况下,应以控制质心侧偏角为主.
(1)基于质心侧偏角(β)的滑模变结构控制
汽车行驶的期望状态符合线性二自由度车辆模型,因此,当以质心侧偏角为控制变量时,可将质心侧偏角对前轮转角的响应改写到滑模面上,有:





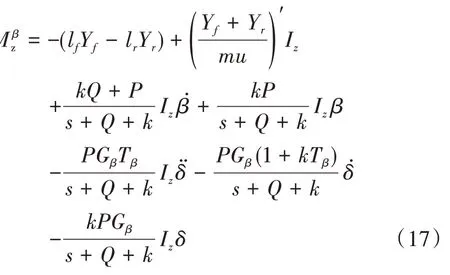
式中,Yf,Yr分别为前后轴两侧轮胎所受的总侧向力,m为车辆总质量,Iz为车辆绕z轴的转动惯量.
(2)基于横摆角速度(γ)的滑模变结构控制
与基于质心侧偏角的滑模变结构控制同理,将横摆角速度对前轮转角的响应改写到滑模面上,如式(18)所示:

其中,Te,Gγ同样是由车辆结构参数所确定的与横摆角速度相关的增益系数.由到达条件Ṡ+kS=0(k>0)得:


由此,可得到横摆角速度控制的附加横摆力矩

2.4 基于全轮转矩优化分配控制的下层控制器
在进行车轮力矩控制分配时需要明确合适的优化目标,本文所提出的优化目标是从轮胎利用率的角度来考虑的.同时用轮胎利用率来表征车辆的稳定裕量,轮胎利用率越低,稳定性裕量越高,车辆稳定性越好.轮胎利用率的函数如下式:

车辆的稳定裕量表达式为:

其中,i(i=1,2,3,4)分别代表的是左前轮、右前轮、左后轮、右后轮.μi代表各轮的路面附着系数,Fxi,Fyi,Fzi分别代表各轮所受的纵向力、侧向力和垂向力.Ci代表各轮权重系数,在实际工况中,由于车辆自身限制,可能会出现某轮所需驱动转矩超出电机峰值转矩的现象,因此,在本文中以各轴垂向载荷之比作为权重系数Ci来调整转矩分配,即如式(24)所示.
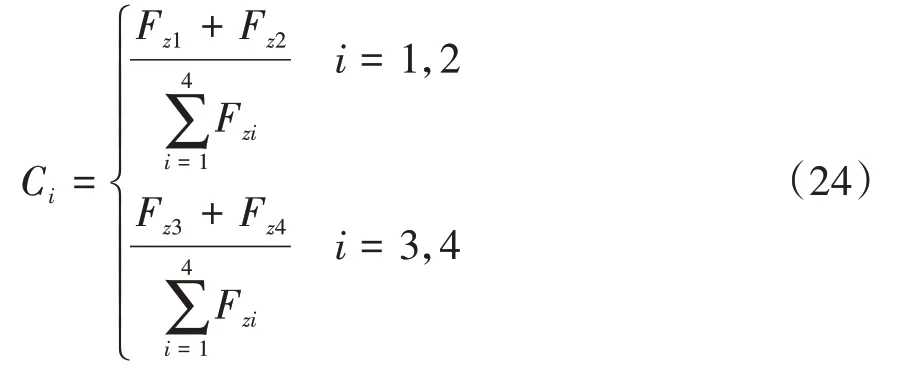
下层控制器轮胎力优化分布控制的优化目标是四个轮胎利用率的最小平方和.优化分配目标函数J如下式所示:

在实际工况中由于车轮的侧向力无法进行人为控制,所以实际控制量只选取了各个车轮的纵向力.同时,由于实际中车轮纵向力和侧向力具有一定的耦合关系,本文采用的补偿方法是在优化纵向力分配的同时,尽可能保留电机的裕量,降低整车的控制难度.由此进一步改进优化分配目标函数,得到转矩优化目标分配函数,如式(26)所示,r为轮胎半径,Txi(i=1,2,3,4)为各车轮所受驱动转矩.通过优化算法求解上述目标函数,可得控制转矩.

3 控制策略验证
本文使用CarSim建立了轮毂驱动电动车辆动力学模型,其主要参数如表3所示.同时在Matlab/Simulink环境下搭建了双层车辆稳定性控制策略模型,并利用Carsim和Simulink进行了联合仿真.稳定性控制策略联合仿真模型如图6所示.在Carsim整车模型中,包括设定的车辆动力学模型,驾驶员模型以及仿真工况;在Simulink中建立了轮毂电机驱动控制系统模型、动力学分析模块、联合滑模变结构控制模块和力矩最优分配模块.仿真所使用的工况如图7所示.

图6 稳定性控制策略联合仿真模型Fig.6 Model of stability control strategiesco-simulation

表3 车辆模型主要参数Table 3 Main parameters of the vehicle model

图7 换道工况Fig.7 Lanechangecondition
控制策略联合仿真模型的基本原理是通过接收Carsim模型的车辆行驶状态参数进行动力学分析,以理想质心侧偏角和横摆角速度为控制目标,运用滑模变结构控制的方法得出附加的直接横摆控制力矩.最优分配模块根据附加的直接横摆控制力矩,以轮胎利用率最小为优化目标,得出各个车轮的驱动力矩.驱动的力矩若符合电机模型的动力性限制,则将根据电机动力性特性做出调整.然后驱动力矩将传送到Carsim模型,使车辆根据设定的工况行驶.
3.1 高附着路面(μ=0.85,v=140km/h)仿真结果
图8为在附着系数μ=0.85的路面,初始车速v=140km/h的工况下进行的标准换道工况仿真.仿真时驾驶员模块所输出的转向角信号如图8(a)所示,图8(b)、(c)分别为期望参数曲线以及车辆在无控制、基于横摆角速度(γ)的滑模变结构控制和基于质心侧偏角(β)的滑模变结构控制控制策略下车辆各状态参数的变化曲线.图8(d)为车辆在以上三种控制状态下的β-β̇相平面图.

图8 在μ=0.85,v=140km/h时的仿真结果Fig.8 Simulation resultswithμ=0.85 and v=140km/h
可以看出,在该速度和路面条件下进行换道,不具备控制策略时车辆已经失稳,质心侧偏角和横摆角速度均发散,无法回到稳定状态;而本文所提出的基于滑模控制的双层控制策略可以明显减小换道时的质心侧偏角和横摆角速度,车辆最终趋于稳定,有效提高了车辆稳定性.
同时综合对比图8中不同控制策略的仿真结果可以看出,虽然在该极限工况下受限于车辆实际结构,所提出的控制策略与期望质心侧偏角和横摆角速度相比有一定程度的滞后,但其曲线趋势与期望曲线相同.同时根据β-β̇相平面图可以看出,轮毂驱动电动车辆在高附着路面上以较高速度转弯的工况下,基于横摆角速度(γ)的变结构滑模控制策略相较于基于质心侧偏角(β)的滑模控制策略,车辆参数曲线收敛更快,质心侧偏角与质心侧偏角速度幅值更小,具有优势.因此,车辆在高附着路面高速转向时,使用横摆角速度(γ)作为控制变量,可以使车辆性能表现更好.
图9为本工况下,车辆在无转矩分配控制与采用所提出的转矩分配控制算法时的各轮驱动转矩Txi曲线,Txi为负值时表示制动力矩.可以看出所提出的转矩分配控制算法具有明显的控制效果.

图9 在μ=0.85,v=140km/h时的驱动转矩Fig.9 Drive torque withμ=0.85 and v=140km/h
3.2 低附着路面(μ=0.1,v=60km/h)仿真结果
图10为在附着系数μ=0.1的路面,初始车速v=60km/h的换道工况下进行的工况仿真.仿真时驾驶员模块所输出的转向角信号如图10(a)所示,图10(b)、(c)分别为期望参数曲线及三种不同的控制策略下车辆各项参数的变化曲线.从图中可以看出,若不采取控制策略,则此时车辆将会进入失稳状态,质心侧偏角和横摆角速度均不收敛;而采取了变结构滑模控制策略后,车辆的质心侧偏角和横摆角速度均保持在合理范围内并最终收敛.

图10 在μ=0.1,v=60km/h时的仿真结果Fig.10 Simulation resultswithμ=0.1 and v=60km/h
对图中不同控制策略的控制效果进行分析可得,在低附着路面上进行行驶时,由于路面附着系数较低,车辆濒临失稳,因此与期望参数曲线存在较大差距.但根据β-β̇相平面图,在该工况下,虽然基于质心侧偏角(β)的控制策略与基于横摆角速度(γ)的控制策略相比,质心侧偏角和质心侧偏角速度幅值更大,但收敛效果更好,基于横摆角速度(γ)的控制策略曲线一直存在较大抖动.因此,综合来看此时基于质心侧偏角的滑模控制策略比基于横摆角速度的滑模控制策略效果更好.
图11为本工况下,车辆在无转矩分配控制与采用所提出的转矩分配控制算法时的各轮驱动转矩Txi曲线.可以看出在该工况下,所提出的转矩分配控制算法具有明显的控制效果,同时由于该工况下路面附着系数过小,与前一工况相比,最终车辆左右轮之间存在一定的驱动力矩差值,以平衡由于车轮打滑所引起的车辆失稳.

图11 在μ=0.1,v=60km/h时的驱动转矩Fig.11 Drivetorque withμ=0.1 v=60km/h
综上所述,在不同附着系数路面上、不同的车速时,车辆考虑的主导控制参数不同.车辆在高速弯道、高附着路面上行驶时,主要呈现的是动力学特性,侧向加速度过大是失稳的主要原因,控制的主要目的是稳定性.此时基于横摆角速度控制的效果优于基于质心侧偏角的控制.反之,车辆的运动学特性表现更明显,质心侧偏角过大是失稳的主要原因,因此,此时基于质心侧偏角的控制策略更好.
4 结论
本文研究了轮毂驱动电动车辆的动力学稳定性问题.分析了车辆横摆角速度与质心侧偏角对车辆稳定性的影响.针对轮毂驱动电动车辆的稳定性问题,基于直接横摆力矩控制原理,设计了双层车辆稳定性控制器,其上层控制器采用了滑模变结构控制策略,下层则基于轮胎利用率最优对转向时各轮驱动力矩进行了最优分配.通过仿真验证了所设计的控制器有效性和鲁棒性,且分别验证了基于质心侧偏角和基于横摆角速度滑模变结构控制策略在低附着路面和高附着路面的有效性和优越性.

