d-作用下保测系统的限制敏感性
张瑞丰, 朱晓凡
(合肥工业大学 数学学院,合肥230601)
1 引 言
1948年,Shannon将统计物理中的概念引申到通道通信的过程中时提出了Shannon熵的概念,开创了“信息论”.随后,1959年,Kolomogorov和Sinai借助Shannon信息论中的思想,引入了测度熵的概念,首次将熵与动力系统结合起来.之后Adler,Konheim和McAndrew于1965年在拓扑动力系统中用开覆盖定义了连续映射的拓扑熵.1971年,Bowen利用分离集和张成集给出了拓扑熵的等价定义.
1971年,Ruelle[1]首次严格的给出了初值敏感依赖的定义,受到人们的广泛关注.1986年,Devaney把初值敏感依赖作为定义动力系统混沌的重要条件,给出了比Li-Yorke混沌更直观的定义——Devaney混沌.熵和敏感性都是反映系统复杂程度的重要指标,敏感性和熵之间的关系也一直是专家学者感兴趣的研究方向.2005年Cadre和Jacob在文献[2]给出了两两敏感的概念,并说明弱混合蕴含两两敏感,同时证明了正熵蕴含两两敏感.之后,2012年,Domenico Aiello和Hansheng Diao[3]在其基础上给出了限制敏感性和限制两两敏感的定义,并研究了限制敏感性、限制两两敏感性与测度熵之间的关系.
2 准备知识
Λn={g=(g1,g2,…,gd)∈d∶|gi| λn=#Λn,#Λn代表集合Λn中元素个数. 定义1[6]设(X,B,μ)是一个概率空间,G为作用在空间上的d-作用,若对∀g∈Λn和∀B∈B,都有 g-1B∈B且μ(g-1B)=μ(B), 则称(X,B,μ,d)是一个保测系统. 定义2[6]设(X,B,μ,d)是一个保测系统,如果对任意∀g∈Λn满足g-1B=B的B∈B,必有μ(B)=0或μ(B)=1,那么称系统(X,B,μ,d)是遍历的. 定义3[6]设(X,B,μ)是一个概率空间,μ∈M(X),G为作用在空间上的d-作用A={A1,A2,…,Ak}是一个有限可测剖分,定义剖分A测度熵为 进一步定义G关于剖分A的测度熵为 定义G关于μ的测度熵为 hμ(G)=suphμ(G,A), 这里A取遍X所有有限可测剖分. 定义4(X,B,μ,d)是一个保测系统,ρ是X上与测度μ相容的度量.如果对μ-a.e.x∈X,存在δ>0,a>0,使得对所有ε>0,存在n∈,及存在g∈Λn有 μ{y∈Bε(x)∶ρ(gx,gy)>δ}>0, 则称(X,B,μ,d)是限制敏感的. 定义5(X,B,μ,d)是一个保测系统,ρ是X上与测度μ相容的度量.如果存在a>0,δ>0使得对μ×μ-a.e.(x,y)∈X×X,存在n∈,及存在g∈Λn使得 ρ(gx,gy)>δ, 则称(X,B,μ,d)是限制两两敏感的. 称δ为敏感性常数,a为渐进率,根据定义,如果δ为敏感性常数,则任意δ′<δ也是敏感性常数;如果a为渐进率,则任意a′>a也是渐进率. 性质1设(X,B,μ,d)是一个保测系统,ρ是X上与测度μ相容的度量,且ρ是μ-正则的,如果(X,B,μ,d)是限制两两敏感的,则其也是限制敏感的. 证假设(X,B,μ,d)是有限制两两敏感常数δ和渐进率a的限制两两敏感的,由定义可知对a.e.x∈X,a.e.y∈X,存在n∈,及∃g∈Λn,使得ρ(gx,gy)>δ. 因为ρ是μ-正则的,对上述x,取c>0,使得 (1) 考虑对任意ε≤δ,εΜ=sup{ε′<ε∶μ(Bε′(x))<μ(Bε(x))}.若μ(BεM(x))=μ(Bε(x)),则取ε′<εM非常接近εM,使得 μ(Bε(x)Bε′(x))>0,μ(Bε′(x))≥cμ(Bε(x)). (2) μ(Bε(x)Bε′(x))>0. 根据(1)式可得 (3) 根据上述x和ε′,对a.e.y∈Bε(x)Bε′(x),存在n∈,及∃g∈Λn,有ρ(gx,gy)>δ. 由(2),(3)式可知 μ(Bρ(x,y)(x))≥μ(Bε′(x))≥cμ(Bε(x)), 故 所以(X,B,μ,d)限制敏感的. 性质1说明了在ρ是μ-正则的情况下,限制两两敏感性比限制敏感性强.敏感性和熵都是反映动力系统复杂程度的量,自然地,想要研究敏感性与熵之间的关系.文献[7]中给出了amenable群作用系统下非遍历情形的Shannon-McMillan-Brieman定理,amenable群包括所有的有限群,紧致群和可解群,d是一类特殊的amenable群. 引理1(Shannon-McMillan-Brieman定理:非遍历情形) 设(X,B,μ,d)为一个保测系统,G为一个可数离散amenable群,对G中任何满足增长条件的temperedFφlner序列{Fn}以及X的有限可测剖分P,对μ-a.e.x∈X都有 且 定理1设(X,B,μ,d)是一个保测系统,μ是X上的无原子概率测度,ρ是X上与测度μ相容的度量,且是μ-正则的,令A={A1,A2,…,Ak}是X的一个有限可测剖分使得对所有∀i有diamAi<δ,令hμ(G,A)是G关于剖分A的测度熵.如果(X,B,μ,d)是有渐进率a和限制两两敏感常数δ的限制两两敏感的,则有 证假设(X,B,μ,d)是有限制敏感常数δ和渐进率a的限制两两敏感的,由定义知:选x∈X使得对μ-a.e.y∈X,存在n∈,及∃g∈Λn使得 ρ(gx,gy)>δ. (4) ρ(gx,gy)<δ, ∀g∈Λn (5) 由于ρ是μ-正则的,存在c>0使得 因为μ是无原子概率测度,故当r→0时,μ(Br(x))→0.对任意的整数n,令εn满足 e-(n-1)c>μ(Bεn(x))≥e-nc. 于是 两边取对数得 即 由题设可知(X,B,μ,d)是有限制敏感常数δ和渐进率a的限制两两敏感的,则存在 及存在g∈Λi,使得ρ(gx,gy)>δ.由(5)可知y∉Cn(x),断言得证. 故由断言得 令 由Shannon-McMillan-Brieman定理 定理1说明了对于一个保测系统来说,限制两两敏感意味着正测度熵,自然地,想要知道限制敏感与熵之间的关系.在证明定理2的过程中要用到文献[8]中的amenable群作用下遍历版本的 Brin-Katok熵公式: 其中BFn(x,ε)={y∈X∶ρFn(x,y)<ε}={y∈X∶ρ(gx,gy)<ε,对任何g∈Fn}. 定理2设(X,B,μ,d)是一个遍历系统,μ是无原子概率测度,ρ是X上与测度μ相容的度量.如果则对所有x∈X,(X,B,μ,d)是有渐进率a和敏感常数δ的限制敏感的. 证假设对所有x∈X,(X,B,μ,d)不是有渐进率a和敏感常数δ的限制敏感的.存在一个正测集A,使得对∀x∈A和δ>0,存在ε(δ)≤δ,对所有n∈,及∀g∈Λn,有 μ{y∈Bε(δ)(x)∶ρ(gx,gy)>δ}=0, (6) 对这样的n,令 ρn(x,y)∶=max{ρ(gx,gy)∶∀g∈Λn},Bn(x,δ)={y∈X∶ρn(x,y)≤δ}, ρ(gx,gy)≤δ, ∀g∈Λn (7) 故 利用Brin-Katok熵公式,存在x∈A使得 与已知条件矛盾,假设不成立,所以对所有x∈X,(X,B,μ,d)是有渐进率a和敏感常数δ的限制敏感的. 致谢非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.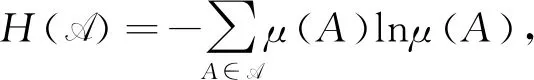
3 主要结果及证明

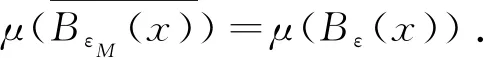





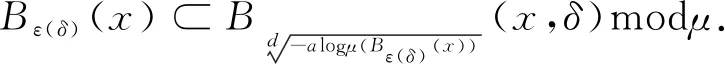


4 结 论

