基于单位脉冲响应的人造地震波模拟和结构抗震随机模拟分析

李雪平 张磊源 魏鹏

(华南理工大学 土木与交通学院∥亚热带建筑科学国家重点实验室，广东 广州510640)

地震动具有很强的非平稳性，地震动随机模型是应用随机振动理论研究结构随机地震反应的基础。20世纪50年代，Housner[1]首次提出利用理想白噪声模型来模拟地震动地面加速度过程。地震动随机模型发展至今，已经建立了一些较好的随机模型，如平稳模型中的Kanai-Tajimi模型[2]、Clough-Penzien模型[3]等，非平稳模型中的强度非平稳模型[4]等。在应用地震动随机模型时，选择合理的模型设计参数对于计算分析具有重要意义。欧进萍等[5]、洪峰等[6]分别利用随机极值理论、强震记录统计分析的结果来确定模型参数。薛素铎等[7]、任文杰等[8]根据我国的抗震规范进行研究，并给出了随机地震动模型参数。

结构动力时程分析的可靠性不仅取决于合理的结构计算模型和精确的计算方法，而且与地震波的输入选择有重要关系[9- 11]。贾宏宇等[12]、黄朝光等[13]采用三角级数法合成人造地震波，该法原理简单,但所得地震波的平均反应谱与规范反应谱有一定差距；江近仁等[14]利用由目标反应谱转换的功率谱合成人造地震波，为了提高精度，需要多次迭代，计算效率较慢；丁佳伟等[15]提出一种能同时满足功率谱与反应谱精度的时频域双控的合成地震波方法；王向超等[16]将数值模拟方法与地震动预测方程相结合，为重大水电工程抗震分析提供了一种地震波合成方法。受限于已有地震动随机功率谱模型的固定形式，通过其模拟的地震波与规范的反应谱存在很大的差异。苏成等[17]直接采用现行《建筑抗震设计规范》(GB 50011—2010)中的规范反应谱，采用谐波合成法[18]模拟了与规范反应谱相一致的人造地震波。

振型分解反应谱法是我国现行规范规定的抗震计算方法，时程分析法是对振型分解反应谱法计算结果的补充计算。现行规范规定，当采用时程分析法时，多条时程曲线计算所得结构底部剪力的平均值不得小于振型分解反应谱法计算结果的80%。

显式时域随机模拟分析是一种针对大型复杂结构的高效非平稳随机振动分析方法[19- 23]，其从工程技术人员较为熟悉的时域分析方法入手，更加简单、高效。以往的显式时域法(ETDM)都是基于精细积分法、Newmark-β法等数值积分方法推导而来，而本文基于单位脉冲的解析响应推导了单自由度和多自由度动力系统的显式时域表达式；然后将单自由度动力系统的显式时域表达式应用于求解地震动随机模型过滤白噪声获得人造地震波，利用其能快速求解响应的特点，通过迭代，确定与规范反应谱相符的谱强度因子，进而高效地模拟指定强度和与规范反应谱相符的人造地震波；最后将本文方法模拟的人造地震波和多自由度动力系统的显式时域表达式应用于结构抗震随机模拟分析，并通过算例进行验证。

1 基于单位脉冲的显式时域表达

1.1 单自由度系统

受动力荷载u(t)作用下的单自由度体系的运动微分方程为：

(1)

将荷载u(t)离散为时刻t0、t1、…、tl处的激励值u0、u1、…、ul，时间步长为Δt。通过数值积分的方法可以把式(1)的解写为离散的递推表达式：

(2)

(3)

当u0=1且ui=0(1≤i≤l),即系统(1)在t0时刻作用单位脉冲激励时，各时刻响应为：

(4)

Zi=TiRi, 1≤i≤l

(5)

式中：

(6)

(7)

e-ζωnti-1(ωDcos(ωDti-1)+ζωnsin(ωDti-1))]/

(8)

则ti时刻的速度表达式为：

(9)

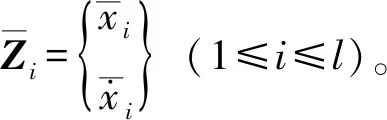
1.2 多自由度系统

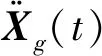
(10)

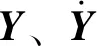
文中采用Rayleigh阻尼模型，对式(10)应用振型分解法，取振型截断数为Nd，则Y(t)可表示为：

(11)

式中：Φ为振型矩阵，{q(t)}为广义坐标向量，且

(12)

将式(12)代入式(11)，并在方程两边左乘ΦT，则式(10)可被解耦成Nd个单自由度体系动力方程：

(13)

根据单自由度结构基于单位脉冲的显式时域表达，第k个单自由度体系响应的显式时域表达为：

(14)

式中，ak,i(1≤i≤l)为相应的二维列向量系数。

将系数ak,i写成：

(15)

式中,bk,i和ck,i分别为ak,i的第1个元素和第2个元素。

那么，第k个单自由度体系在ti时刻的位移响应和速度响应的显式时域表达式可分别表示：

(16)

将式(16)按式(11)进行振型叠加，可以得到多自由度线性结构ti时刻响应的显式时域表达式为：

(17)

(18)

若令

(19)

则式(17)可进一步表示为：

Qi=HiRi, 1≤i≤l

(20)

式(20)即为多自由度线性结构基于单位脉冲与振型分解法的显式时域表达式。

(21)

相比式(20)，采用式(21)计算动力响应可以实现多自由度系统的降维计算，同时也可以减少系数矩阵的储存量,在进行大规模结构动力时程分析时可以显著减少计算量，大幅提升计算效率。

2 地震动随机模型及设计参数

工程中常用的非平稳地震模型为强度非平稳模型[4]，它是将平稳随机过程乘上均匀调制函数来模拟非平稳随机过程。该非平稳模型地震加速度可表示为：

(22)

本文采用Kanai-Tajimi过滤白噪声模型(以下简称为K-T模型)进行研究，该模型的地面加速度功率谱密度为：

(23)

式中：ωg、ζg为滤波器的参数[25]；S0为白噪声的谱强度因子，它是直接与地震动强度有关的参数。

图1 Kanai-Tajimi模型

该模型的覆盖土层运动方程为：

(24)

那么，平稳地面加速度为：

(25)

式(22)中的均匀调制函数采用工程中常用的均匀调制函数[26]，其表达式为：

(26)

式中,t1、t2为主震平稳段的起始时间,c为衰减系数,这些参数取值与震级和场地条件等有关。

3 与规范反应谱相符的人造地震波

3.1 指定地震强度的人造地震波的模拟

采用基于单位脉冲的显式时域法求解运动方程(24)，有：

(27)

式中：

将式(27)代入式(25)可得平稳地面加速度：

(28)

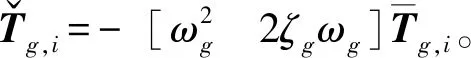
将式(28)乘上均匀调制函数g(t)，可得人造地震波的表达式为：

(29)

参考文献[2]，在表1中给出了当基于K-T模型模拟指定强度的地震波时，在多遇地震、设计地震第一组的抗震设计条件下谱强度因子S0的取值。

表1 K-T模型的谱强度因子S0的取值Table 1 Spectral intensity factor S0 reference value of K-T model 10-4 m2/s3

采用基于单位脉冲的显式时域法,求解K-T模型模拟样本数为10 000条的人造地震波样本。限于篇幅，本文只列出抗震设计条件为8度多遇地震、设计地震分组第一组、场地类别分别为Ⅰ0、Ⅱ、Ⅲ时的计算结果。地震动持时依次取为15、15和20 s，时间步长取为0.02 s。

图2给出了在Ⅱ类场地下的模拟人造地震波样本里的单条地震波时程曲线。图3为在Ⅱ类场地下模拟的10 000条人造地震波的样本方差和K-T模型目标方差的比较，其中目标方差可根据K-T谱的自相关函数[27]求得。为了验证本文方法(单位脉冲+ETDM)的正确性，同时给出了Newmark-β直接法和基于Newmark-β法的显式时域法[28]模拟人造地震波的计算结果。各种方法的计算耗时和最大相对误差列于表2中。由表2可以看出：基于单位脉冲的显式时域法在模拟人造地震波样本时，计算效率较高于Newmark-β直接积分法；基于本文方法得到的结果样本方差与目标方差的符合程度较高，计算结果的最大相对误差均在容许误差范围内。以上说明基于单位脉冲的显式时域法在求解K-T模型模拟人造地震波时具有良好的计算效率和计算精度。事实上，在求解其他平稳模型时，如Clough-Penzien模型等，采用基于单位脉冲的显式时域法也能达到同样的目的，限于篇幅，本文只给出了基于K-T模型模拟人造地震波的结果。

图2 单条地震波时程曲线

图3 样本方差与目标方差的对比

Newmark-β直接积分法和基于Newmark-β法的显式时域法的结果与目标方差的偏差较大，主要原因在于Newmark-β法属于逐步积分法，当取时间步长为0.02 s时，输入的白噪声并非理想白噪声，而是限带白噪声，其带宽为0～50 Hz。

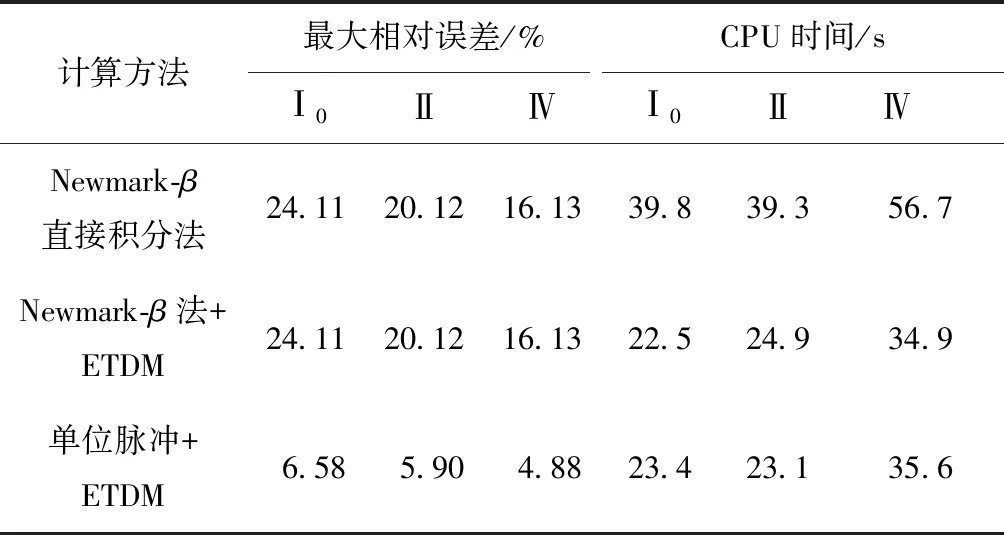
表2 各种方法的计算时间和最大相对误差Table 2 Calculation time and maximum relative error of various methods

3.2 与规范反应谱相符的人造地震波的模拟

我国现行的抗震规范规定，采用时程分析法时使用的地震波的平均反应谱曲线应与规范反应谱曲线在统计意义上相符[29]。对3.1节中利用基于单位脉冲的显式时域法模拟的人造地震波样本进行大量抽样，获得平均反应谱,将其与规范反应谱比较，如图4所示。其中，α为地震影响系数，T为周期。由图可见，根据单一谱强度因子S0模拟的人造地震波样本与规范反应谱在形状上是相似的，但在多数周期点上两者的反应谱数值误差较大。这说明地震动随机模型无法根据单一谱强度因子S0过滤白噪声，模拟与规范反应谱在整个周期内都吻合的人造地震波。

图4 两种反应谱的比较

为模拟与现行规范反应谱相符的人造地震波，采用邓军等[30]在研究时程分析法中选择输入地震记录时，对[0 s,6 s]频段进行划分控制的思想，考虑利用基于单位脉冲的显式时域法能快速求解响应的特点，通过迭代，先确定当结构的基本周期为T时与规范反应谱相符的谱强度因子S0(T)的统计值，进而用于模拟大量与规范反应谱相符的人造地震波。其主要步骤如下：

(1)根据谱强度因子与地震烈度、场地类别有关的特点，确定S0,L和S0,R的初始值，致使[S0,L,S0,R]包含S0(T)所有的可能取值，这里取S0,L=10-4，S0,R=1，利用二分法取S0(T),即S0(T)=(S0,L+S0,R)/2；

(3)计算结构基本周期为T时的平均反应谱值与相应规范反应谱值的相对误差E(α)；

(5)反复进行上述步骤(1)至(4)，直至S0,L-S0,R和E(α)的绝对值满足迭代容许误差ε为止；

(6)得到与规范反应谱相符的谱强度因子S0(T)；

(7)模拟大量与规范反应谱相符的人造地震波。

采用MATLAB编程实现上述步骤。为说明上述修正谱强度因子S0(T)方法的有效性，取[0 s,6 s]内有限个周期点，考虑8度多遇地震、设计地震第一组、Ⅱ类场地、体系阻尼比0.05，利用上述方法得到T点上平均反应谱值与规范反应谱值的对比情况，如图5所示。由图5可见，修正谱强度因子S0后获得的平均反应谱与规范反应谱的吻合度非常高，其他抗震设计条件下的结果也类似，这说明了上述修正谱强度因子S0(T)方法的有效性。

为便于应用，表3中给出了采用K-T模型时，在7度、8度和9度多遇地震、设计地震第一组、Ⅱ类场地、体系阻尼比0.05的抗震设计条件下，按本文方法得到的与规范反应谱相符的谱强度因子S0(T)的参考取值。

图5 修正谱强度因子后平均反应谱与规范反应谱的对比

表3 采用K-T模型时部分谱强度因子S0(T)的参考取值Table 3 Partial spectral intensity factor S0(T) reference value when using K-T model 10-4 m2/s3

4 数值算例

分别采用Newmark-β直接积分法、基于单位脉冲与振型叠加法的显式时域法计算A点水平自由度的位移响应，两种方法的计算时间分别为145.9 s和2.1 s。图7给出了单条地震波作用下求得的位移响应，可以看出两种方法的计算结果基本吻合。这说明基于单位脉冲与振型叠加法的显式时域法在进行结构动力时程分析时，具有良好的计算精度和较高的计算效率。

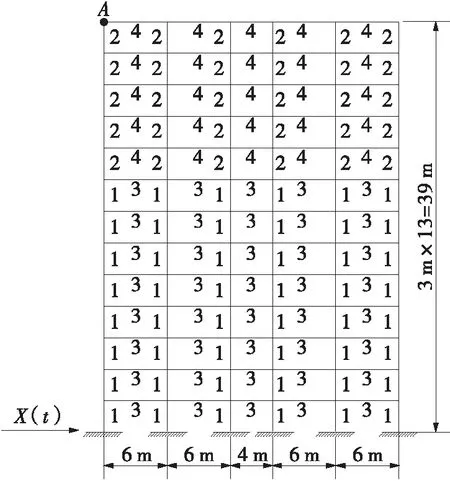
图6 平面框架结构模型

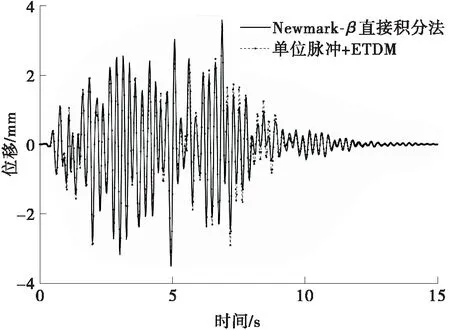
图7 A点的位移响应时程

为验证基于单位脉冲与振型叠加法的显式时域法作为时程分析法时的合理性，采用该法作为显式时域随机模拟分析法，得到结构受随机地震作用时的抗震随机模拟分析结果，并与振型分解反应谱法的计算结果进行对比。层间剪力和质心位移的计算结果如图8所示，层间剪力最大差异为16.54%，质心位移最大差异为13.52%。基于单位脉冲与振型叠加法的显式时域法考虑了地震荷载的随机性，计算结果具有统计意义，两种方法的层间剪力最大差异满足现行规范对采用时程法分析时的要求，说明基于单位脉冲与振型叠加法的显式时域法可用于建筑结构的抗震计算。

图8 层间剪力和质心位移

5 结论

本文基于单位脉冲解析响应推导了线性动力系统响应的显式时域表达式，并将其应用于模拟指定强度和与现行规范反应谱相符的人造地震波，以及结构抗震随机模拟分析，主要得到以下结论：

(1)无论选用何种地震动随机模型，利用基于单位脉冲的显式时域法能快速求解地震动随机模型的地面运动方程的特点，通过迭代，可以高效地模拟大量指定强度的地震波和与现行规范反应谱相符的人造地震波；

(2)基于单位脉冲与振型叠加法的显式时域法在进行大型结构抗震分析时，可以进一步实现降维计算，具有相当高的计算效率，非常适用于大型结构的随机响应时程分析。