分形理论在航天管理中的应用

路明辉、王雪梅 /中国运载火箭技术研究院

一、分形理论简介

1967年，一位名为本华·曼德博的美籍数学家在《科学》杂志上发表了题为《英国的海岸线有多长》的论文。在这篇论文中，本华·曼德博提出了分形概念。海岸线作为自然形成的一部分，其形状和线条是极不规则甚至是毫无规律可言的，单从一小段海岸线无法证明其与其它海岸线的相似性，但是，如果可以将一小段海岸线的尺度进行数百、数千倍地放大，可以发现无论是100km长的海岸线还是10km长的海岸线，它们的外观轮廓都呈现出一种十分相似的状态。曼德博将这种部分与整体以某种方式呈现自相似状态的形体称之为分形。在后续研究中，分形几何学被创建，分形理论也随之生成。

分形形体的自相似性可以归结为统计层面上的相似，也可以体现为局部与整体的完全相同。例如，科赫雪花曲线，如图1所示；谢尔宾斯基图形，如图2所示。

图1 科赫曲线

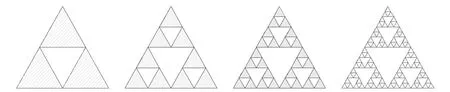
图2 谢尔宾斯基图形

通过深入研究分形理论，可以得到多方面的启示：一是分形理论的核心内容是局部与整体的相似性，可以通过研究局部来揭示整体的复杂特性，在有限知识的基础上对无限进行分析，从而拓展人类的认知领域；二是分形理论揭示了非线性复杂事物中的相似性，可以从杂乱无章的状态中发现规律，揭示某种新秩序；三是分形理论揭示了世间万物并不是孤立存在的，事物之间存在着普遍联系。

分形理论作为一种新学科、新理论，现已广泛应用于信息技术、建筑、艺术，以及管理等诸多领域中。

二、分形管理的特点

管理科学是一门综合性的科学，在管理方法及管理手段等方面都会呈现出一定的层次性。从基层管理到高层管理、从处室到部门、从科技管理到经济管理，也会呈现出一定的自相似性。在知识经济社会里，分形理论或将成为管理科学的基础理论之一。

整体由局部组成，局部可以用来映像整体；局部中的任何一个细微的元素也可以反映局部的性质特征，这就是所谓的元素映像系统，这是分形理论中最具代表性的哲学基础之一。换句话说，分形理论的管理应用，主要体现在各种结构本身的自相似性上。这一点在分形几何中也得到了一定的体现，也就是“系统是部分按某种规律的组合”的基本思想。

基于上述思想，我们可以将企业内的各单位定义为“分形单位”，处室甚至每一位员工都类比为分形管理中的“分形单元”，通过分析归纳各分形单位和分形单元的特征和内在联系，运用部分与整体间的自相似性，则可以归纳总结出企业本身的结构特点，然后，在此基础上进行评判改进，实现组织架构的优化。

分形理论的自相似性运用到企业管理中，可以发现如下规律：

一是结构本身具有自相似性。分形单位的结构设置方式是将不同分形单元，划分成为不同层级，再采用相同的设计原则将各分形单元和层级进行非集中式构造。因此，各分形单元和层级间在结构方面拥有一定的自相似性。

二是分形单位在功能方面具有自相似性。处于任何分形单位内部的每一个分形单元都具有相同的特性，都是同时具备智能与权限的自治体。因此，不同的分形单元之间需要着重强调协同作用。因为，分形单位会使得权利下放，而分形单元本身存在一定的相似性，从而使所有部门的功能会逐步带有一定的相似性。

通过对分形单位的实际情况分析，可以发现分形单位在运行方面具备自组织性。对于分形单位来说，各分形单元在相同目标的驱动下，安排工作时会进行自主调配，进而达到最优的流程设计。这种局部工作和生产方式的自发改善现象，可以归结为分形单位的自组织性，它并非个人行为，而是单位内全体单元共同作用后所呈现出的复杂表现。基于此，可以实现工作质量的自动监督，以及生产要素的自动合理分配，从而使得分形单元间的工作更加协同、高效；同时，各分形单元在总体目标牵引下，可以自主优化资源配置，协调安排生产进度，最终达到效益最大化。

三、分形理论在航天管理中的应用

经过60余年的发展，中国运载火箭技术研究院目前正处于快速发展期和战略转型期，也处于重要的战略机遇期。作为总体和项目承担单位，研究院的管理模式已从传统的直线式职能管理模式转变为职能管理与项目管理相结合的矩阵式管理模式。此种模式可以实现计划信息与产品信息的有效结合，在计划编制过程中，可以根据产品研制特点进行细化分解，把每一项任务、工作直接分配到一线员工的工作桌面，减少信息的传递环节，实现信息的快速、有效传递；同时，通过信息的实时共享，可以实现信息的基本透明，将串行的各种流程并行化，从而提高管理效率。

1.研究院分形管理的维数计算

目前，研究院的组织机构按照“研究院→部、所、厂、公司→车间、处、室、部门→班组”等四级管理机构进行，如图3所示。其中，作为研究院组成部分的部、所、厂、公司的组织机构由车间、处、室、部门组成，如图4所示。而处、室、部门则由各个班组组成，如图5所示，班组是研究院各级组成机构的基本单元。由图3—图5可以看出，此四级管理机构在组成形式上存在自相似性，符合分形管理的特点，并且可以看作是谢尔宾斯基分形形式。

图3 研究院的组织机构

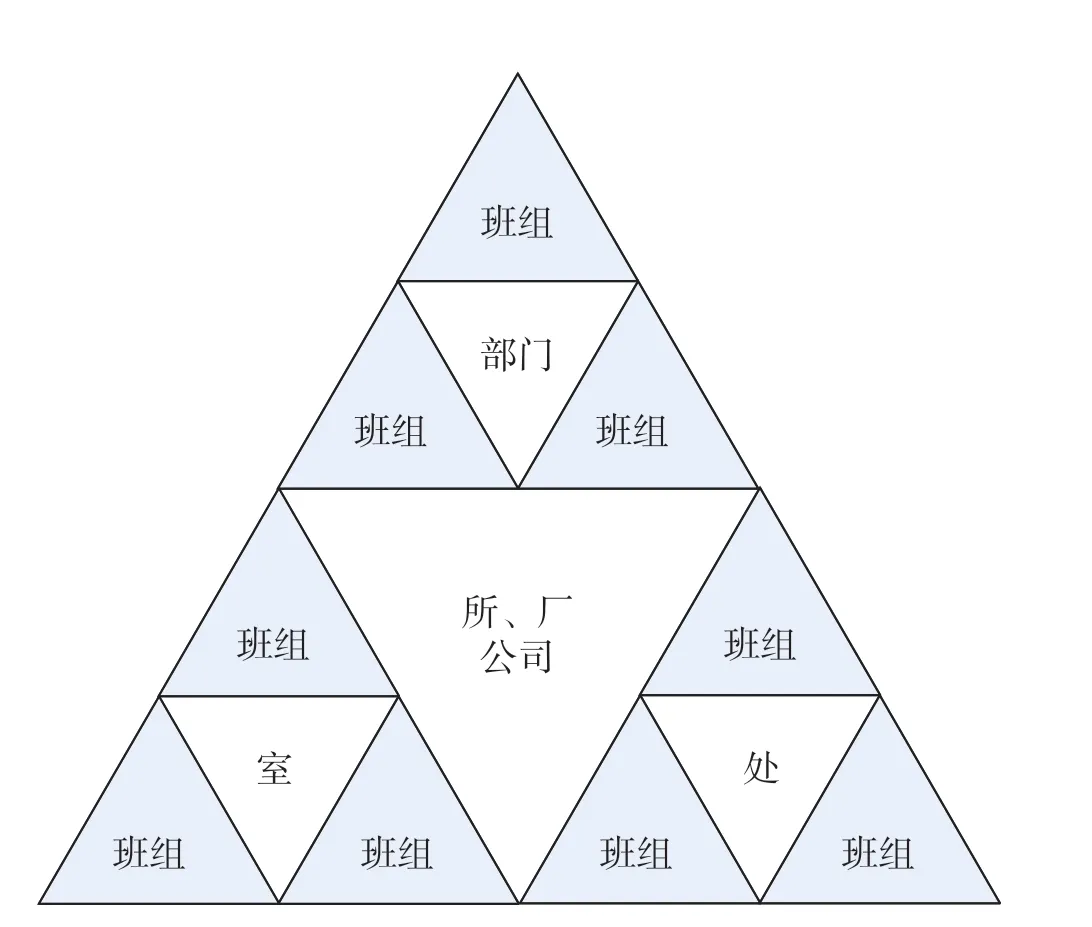
图4 部、所、厂、公司的组织机构

图5 处室的组织机构

分维，又称分形维或分数维，其是作为分形的定量表征和基本参数。长期以来，人们习惯于将点定义为零维，直线为一维，平面为二维，空间为三维，分维所表征的是组成整体的各部分的复杂程度，其维数（Df）可以通过公式：Df=InK/InL进行计算，其中L为某分形单元沿其每个独立方向扩大的倍数，K为得到的新分形单元是原分形单元的倍数。由于研究院管理系统属于谢尔宾斯基分形形式，因此其分形维数为Df=In3/In2≈1.585。

根据计算结果可知，研究院分形管理的维数为1.585，介于一维（直线）和二维（平面）之间。从上面的四级管理机构划分来看，如果信息在传递过程中直接按照点对点的方式由最高层级到最低层级之间进行逐级传递，那么此时分形管理的维数为1；而如果信息传递过程中，同样一项任务由第一层级院级下达到第二层级的每个单位，第二层级下达到第三层级每个处室，第三层级下达到第四层级每个班组，并且在每一层级每个组成部分之间同样存在信息传递的过程，则此信息传递过程属于平面传递，其分形维数为2。由此可见，分形维数与信息传递或者是任务分解的路径和复杂程度有关，维数为1属于直线类型，即上下级之间直接下达并负责；维数为2则属于平面类型，即不仅有纵向的传递，还有横向的传达，属于多级负责类型。

2.分形理论在研究院航天管理中的应用

由于航天管理必须统筹兼顾产品质量和工作效率，分形理论的分形维数将为研究院航天管理提升提供重要的考量依据。

目前，研究院航天项目研制任务较为繁重，这一形势要求研究院相关管理单元在信息传递和工作分解过程中，要提高沟通效率，要做到沟通流程清晰可控；要加强设计单位和生产单位之间的横向联系，同时，班组、处室、单位之间也要加强协调，以避免信息的直线型传递。据以此，研究院的分形维数要大于1（直线型），并且分形维数越大，表明各单元间的沟通联系越紧密。

与此同时，研究院的研制任务正在由国家指令性计划逐步转变为国家任务需求与民用航天需求相结合、由单一的项目研制转变为多领域发展相结合的情况。在此形势下，研究院必须要提高管理效率，要做到快速响应，高效管理，这就要求缩减管理线路，优化资源配置。从这一角度来讲，研究院的分形维数要小于2（平面型），并且分形维越小，越能简化管理中的繁琐过程，提高管理效率。

由以上分析可以看出，统筹考虑航天管理中的质量控制与管理效率问题，研究院项目管理的分形维数应介于1和2之间，而通过模型计算可知，此维数为1.585，该数值科学、直观地表征了研究院在航天管理过程中，部分和整体之间信息传递或项目管理的复杂程度。

分形理论揭示了分形形体的自相似性，为人们从局部中认识整体和从整体中认识局部提供了一种思路，该理论也直观地展示了整体与局部之间多视角、多层面、多维度的联系方式。

本文将分形理论应用于航天管理之中，针对研究院的组织机构及项目研制工作的特点，将其看作是谢尔宾斯基分形，并计算了其分形维数。此分形维数表示了航天管理中部分和整体之间信息传递或项目管理的复杂程度，以一种全新的视角对航天管理的特点进行了说明，为研究院提升管理效率提供了理论支撑。