基于需水过程的灌区实时渠系优化配水模型及应用

马建琴 赵子伟

摘 要：针对灌区灌溉规划用水与作物实时需水不匹配的问题，建立了基于作物需水过程的渠系实时优化配水模型，以下级渠道配水结束时间为决策变量，以灌区时段缺水率之和最小和渠系输水损失量最小为目标，采用遗传算法求解模型。结果表明：与经验法编制的配水方案进行对比，各级渠系配水时间搭配更加合理，渠道配水流量波动小;灌水量配置更符合作物实际需水要求，与作物实时需水耦合度更高，灌区各时段缺水率之和减小了13.6%，配水时间减少了2.5 d，渠系输水损失量占比减少了6.3个百分点，渠系配水达到了省时高效、节约用水的目标。

关键词：实时渠系配水;优化配置;需水过程;灌溉制度;时段缺水率

中图分类号：S274.3;TV146 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.05.030

Abstract： Aiming at the issue that the existing water distribution plan in irrigation area cannot meet the actual operation of canal system and the real-time water demand of crop growth and development， a real-time optimal water distribution model of canal system based on crop water demand process was established. The end time of lower-level canal water distribution was the decision variable， the objective function was the minimum sum of water shortage rate and the minimum water loss of canal system and used the genetic algorithm to solve the model. The results show that compared with the water distribution scheme prepared by the empirical method， the water distribution time of all levels of canal system is more reasonable and the fluctuation of water distribution flow is small; the irrigation allocation is more in line with the actual water demand of crops， and the coupling degree with the real-time water demand of crops is higher， the water shortage rate of irrigation area is reduced by 13.6%， the water distribution time is reduced by 2.5 days and the water transfer loss of canal system is reduced by 6.3%. The canal water distribution achieves the time-saving， efficient and water-saving goals.

Key words： real time canal system water distribution; optimize configuration; water demand process; irrigation schedule; water shortage rate in period

目前我國大部分灌区在制定用水计划时仍按经验方法手工编制，这会导致渠系输水时间较长、配水流量小和灌溉水资源浪费等问题。在农业灌溉水量本就不足的情况下，农田灌溉水利用系数仅有0.548[1]，远低于发达国家水平，农业用水形势十分严峻。如何通过科学手段分配灌溉水量，减少输水损失，提高灌溉水利用系数，是目前灌区管理工作中急需解决的问题。

国内外学者为解决渠系优化配水问题已经做了大量研究，并提出多种优化配水模型[2-3]。根据研究目标可分为两大类：第一类以经济效益为主体，研究目标为灌溉管理部门收益最大[4]、作物产量最大[5]等;第二类以灌区渠系运行为主体，研究目标为配水时间最短[6]、上级渠道配水流量平稳[7]、输水损失量最小[8]等。然而，这两类优化模型都只考虑灌溉管理部门收益或渠系运行条件单方面的影响，忽略了作物在时间尺度上的需水要求，所得配水计划不能满足作物实时需水。作物需水是时间尺度上的问题，很难找到一个普遍的量化标准，因此本研究考虑通过土壤含水量的变化过程来反映作物需水过程[9]，在此基础上建立渠系实时优化配水模型，既满足灌区渠系运行要求，又满足作物生长发育实时需水[10]，为灌溉管理部门灌水决策提供依据。

1 渠系实时优化配水模型的建立

1.1 渠系实时优化配水模型

本研究以作物时段缺水率之和最小、渠系输水损失量最小为目标，决策变量为下级渠道的配水结束时间。依据土壤含水量的动态变化确定作物的需水情况，以作物的实际需水量为配水数据基础来制定渠系优化配水方案。要求配水方案满足：①水量满足作物需水要求;②配水流量不超过各级渠道设计流量;③配水时间在轮期内。由于在配水量相同的情况下，配水流量越大，配水时间越短，其时段缺水量越小，输水损失也越小，因此需使各级渠道尽可能达到设计流量，并保持上级渠道输水平稳。

1.1.1 目标函数

（1）以作物水分亏缺指数（CWDI）来表示作物生长发育过程中的缺水情况。CWDI即某时段作物实际需水量和实际供水量之差与该时段作物实际需水量之比，考虑了作物的实际需水和供水过程，与作物实际生长过程结合起来，能够较真实地反映作物水分亏缺状况。每个时段的作物水分亏缺指数称为时段缺水率，以各时段缺水率之和CW最小为目标函数：

式中：qij为第i时段第j渠道（j为下级渠道编号）的配水流量;tij为第i时段第j渠道的配水时间。

（2）在灌区灌水过程中，会产生一定的渗漏损失，为使灌溉过程达到节水的目的，应使渠道输水损失量最小[10]。假设上级渠道的配水流量为qs，下级渠道总共有n条，各条下级渠道的设计流量为qj（j=1，2，…，n）。配水过程中所有渠道的输水总损失量Q最小的目标函数为

1.1.2 约束条件

1.2 作物需水过程计算

作物需水过程是指作物需要灌溉的水量在生育期内某一时间尺度下的分配过程，它与作物种类、作物种植面积有关，还受到灌区土壤水分变化和降水等影响[11]。对于旱作作物，通过土壤水量平衡方程可以很好地表示土壤水分变化对作物耗水的影响以及作物的需水要求[12]，因此本文根据灌区的实测土壤含水率日变化数据，利用土壤水量平衡方程来反映作物需水量变化情况。后一天的土壤含水量是由前一天的土壤含水量、降雨量、灌水量、作物实际需水量以及计划湿润层增加的水量共同确定的[13]，土壤水量平衡方程为

在进行计算时，有效降雨量计算采用文献[14]中的计算方法。作物实际需水量通过参考作物需水量计算得到，先由修正的彭曼公式代入气象资料计算出参考作物需水量ET0，再乘以该生育阶段的作物系数Kc和该土壤含水量水平下的土壤水分修正系数Kw，即可计算得到实际作物需水量[15]，计算公式为

式中：ETjt为第t时段的实际作物需水量;ET0t为第t时段的参照作物需水量;Kct和Kwt为实时的作物系数和水分胁迫系数，其中作物系数参考裴源生等公式[16]根据土壤含水量推求。

（1）灌水深度。各级渠道每天灌入田间的水量用灌水深度表示，即

式中：ηf为该灌区的灌溉水利用系数，参考河南省渠村灌区农田资料取值为0.576[17];Xjt为第t天第j条下级渠道灌入田间的水量，m3;Sj为第j条下级渠道的控制面积，hm2。

（2）净灌溉需水量W净j。通过各下级渠道控制面积及灌水深度可得到该区域的净灌溉需水量：

式中：W净j为第j条下级渠道控制面积的净灌溉需水量，m3;IRj为第j条下级渠道控制面积的灌水深度，mm。

2 基于遗传算法的模型求解

2.1 算法编码

根据灌区渠系情况，每条渠道的参数都已经确定。进行渠系优化配水决策，就是在已知各下级渠道可配水量时，计算该渠道的配水开始时间和结束时间。决策变量选取下级渠道配水开始时间和配水结束时间。该时段配水水量除以配水流量可以得到配水时间，配水结束时间减去配水时间可以得到配水开始时间，因此在编码时只需对配水结束时间编码即可。根据灌区轮期计划，采用二进制编码方案（见表1），最大时段为25=32，每条下级渠道的编码长度为5，N条下级渠道的编码长度为5N。

2.2 适应度函数设计

由于本研究以减少渠道的输水损失和时段缺水率之和最小为目标函数，因此其数值越小效果越好。本文中轮期、水量约束条件在编码设计的过程中已经得到满足，水量平衡约束条件为软性约束，应保证任意时段均满足，处理时比较麻烦，因此在适应度函数中考虑，设置适应度函数Z为

式中：W为灌区配水过程中的配水总量，m3;前项主要反映输水损失量最小的目标函数要求，后项主要反映时段缺水率之和最小的目标函数要求;α1、α2为目标函数的权重值。

轮期约束条件为硬性约束条件，必须满足，如不满足，则适应度为零，即Z=0。

2.3 选择、变异、交叉

根据计算所得群体中每个个体的适应度值大小，选用轮盘赌法对种群中的个体进行选择，使进化过程中适应度值较大的染色体有更大的概率参与选择;交叉运算采用单点交叉的方式，按照设定的交叉概率Pc在群体中随机选取两个个体进行单点交叉，产生新个体;变异运算采用概率变异法进行，Pm为变异概率。

2.4 控制参数的确定

种群规模为目标函数中的决策变量配水结束时间tej，为使算法更加稳定可靠，设置初始种群数目为150，种群规模为下级渠道数量j，交叉概率為0.6，变异概率为0.001，迭代次数为500次。

3 模型的应用

3.1 研究区域介绍

研究区域选取濮阳市西部渠村灌区，地处大陆性季风气候区，蒸发量大，降雨较少。渠村灌区从渠村引黄闸引黄河水灌溉，由输水总干渠进行配水，总干渠上共布设输水下级渠道19条，属于国家大型灌区，渠系网络可以执行灌区日常灌排任务。灌区设计灌溉面积12.87万hm2，占灌区总耕地面积的48%。2013年实际灌溉面积8万hm2，占设计灌溉面积的62%。根据渠村灌区2014年统计资料可知，在研究时段内只种植冬小麦一种作物，灌区来水主要靠引黄水与地表水供给，实际来水流量为60 m3/s，灌水方式采用组内轮灌，组间续灌，各轮灌组内出水口的轮灌顺序可灵活调度[18]。

根据渠村灌区上下级渠道设计流量，由轮灌组分组公式确定轮灌组数，通过各条渠道的控制面积乘以灌水定额可以计算出每条渠道的灌水总量[19]。各条渠道的设计参数见表2。

3.2 模型参数

依据灌区冬小麦全生育期内土壤含水率日变化数据和气象资料，选取2013—2014年度和2014—2015年度的冬小麦全生育期逐日试验数据，采用修正的彭曼公式，根据气象资料计算得出参考作物需水量ET0。图1为2013—2014年度和2014—2015年度灌区冬小麦参考作物需水量ET0在作物全生育期内的逐日变化趋势，图2为2013—2014年度冬小麦全生育期内逐日作物系数和逐日土壤水分修正系数变化情况，图3为2014—2015年度冬小麦全生育期内逐日作物系数和逐日土壤水分修正系数变化情况。

根据式（10）将计算出的日参考作物需水量乘以当日作物系数和土壤水分修正系数，得到冬小麦作物需水量逐日变化趋势，见图4。

冬小麦的需水强度日变化规律主要由冬小麦的生理特性和灌区气候决定，从图4可以看出冬小麦需水最小值出现在越冬期，需水高峰期主要出现在生长200 d以后，也就是4—5月，此时正是冬小麦的出穗灌浆期。该阶段是冬小麦的需水关键时期，必须保证作物的需水要求。

4 结果分析

根据灌区实测土壤含水率数据和气象资料，以2013—2014年度冬小麦全生育期试验数据为基础构建模型，并采用2014—2015年度冬小麦试验数据验证模型，利用遗传算法求解，计算结果见表3。各时段缺水率之和减小了13.6%，灌溉水能够更加快速地通过渠系到达田间，配水效率显著提高;从输水损失量可以看出，灌区渠系输水损失量占比减少了6.3个百分点，渠系水利用系数从0.80提升到0.87。

4.1 作物灌水量对比分析

依据非充分灌溉理论，当土壤含水率高于作物生长所需土壤含水率下限时不需要灌溉，当土壤含水率低于土壤含水率下限时需要灌溉，以此计算得到作物灌水日期和灌溉水量，得到作物实际灌水过程，即冬小麦全生育期内需要进行3次灌溉，将其与同水平年下经验法制定的灌水过程[20]相比较，见图5。

从图5可以看出，通过对作物需水过程进行计算，生育期内需要进行3次灌溉，所得优化后的作物灌溉制度更加合理，不仅使灌水过程更加贴近作物实际需水要求，而且能够节约更多的水资源。图5 2014—2015年度冬小麦灌溉过程对比

4.2 配水方案对比分析

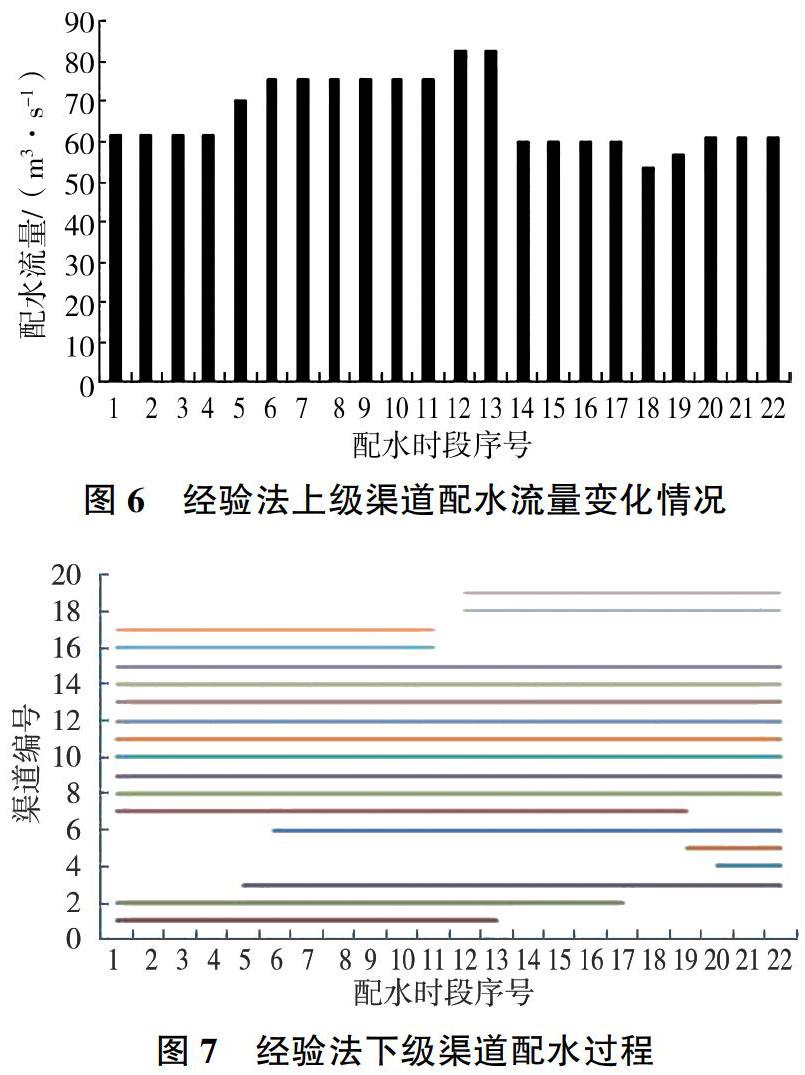
本文选用2014—2015年度冬小麦第1次灌水的实际配水过程，以12 h为1个配水时段，经计算后得到优化后的灌区配水方案，并与经验方法编制的配水方案进行比较分析。

图6、图7为经验法编制的配水方案，图8、图9为优化法配水方案。可以看出，优化方案的配水时间减少了2.5 d，原配水过程上级渠道的各时段配水流量波动较大，并且有多个时段实际配水流量大于灌区来水流量或存在因配水流量较小而产生大量弃水的情况;通过模型优化后的上级渠道配水过程较为均匀，且不超过来水流量限制，便于进行实际配水工作。原经验方法编制的配水方案，其下级渠道的配水时间较为集中，模型优化后下级渠道配水过程各渠道搭配比较合理，配水效果较好。

5 结 论

本研究建立了基于需水过程的灌区实时渠系优化配水模型，并使用遗传算法进行求解。该模型考虑了作物生长发育阶段内需水量的变化过程和渠系输水时产生的输水损失，通过模型得到了满足渠系运行和作物需水过程的优化配水方案。配水结果表明：与经验方法编制的配水方案对比，模型优化后的配水方案各条渠道配水时间搭配合理，与作物实时需水耦合度更高，上级渠道配水流量更加均匀;灌水量分配更加符合作物实际生长发育所需水量，灌区各时段缺水率之和减小了13.6%，配水时间相比减少了2.5 d，渠系输水损失量占比比经验法减少了6.3个百分点，渠系配水达到了省时高效、节约用水的目标。

参考文献：

[1] 包晓斌.高效节水是保证我国农业水资源可持续利用的根本出路[J].中国水利，2018（6）：30-32.

[2] 吴普特，范兴科，牛文全.渠灌类型区农业高效用水模式与工程示范[J].农业工程学报，2003，19（6）：36-40.

[3] 刘颖.灌区渠系优化配水模型建立与求解[J]. 人民黄河，2014，36（6）：107-109.

[4] 贺建文，何英.基于NSGA-Ⅱ遗传算法的丰收灌区优化配水研究[J]. 人民黄河，2020，42（增刊2）：276-278.

[5] 汪志农，熊运章.灌溉渠系配水优化模型的研究[J].西北农林科技大学学报（自然科学版），1993，21（2）：66-69.

[6] 吕宏兴，熊运章，汪志农.灌溉渠道支斗渠輪灌配水与引水时间优化模型[J].农业工程学报，2000，16（6）：43-46.

[7] 郭珊珊，郭萍，李茉.基于多目标遗传算法的渠系配水优化模型[J].中国农业大学学报，2017，22（7）：71-77.

[8] 赵文举，马孝义，刘哲，等.多级灌溉渠系配水优化编组模型与算法研究[J].农业工程学报，2008，24（2）：11-16.

[9] 尚虎君.作物需水量计算模型组件及灌区需水过程研究[D].杨凌：西北农林科技大学，2012：39-57.

[10] PEREA G R，POYATO C E，MONTESINOS P，et al. Optimization of Irrigation Scheduling Using Soil Water Balance and Genetic Algorithms[J]. Water Resources Management， 2016， 30（8）：2815-2830.

[11] 汪志农. 灌溉排水工程学[M]. 北京： 中国农业出版社， 2000：11-45.

[12] 何军，刘增进.基于ET0冬小麦需水量计算及其规律[J].节水灌溉，2013（5）：5-7.

[13] SRIRAMANY S， MURTY V V N. A Real-Time Water Allocation Model for Large Irrigation Systems[J].Irrigation and Drainage Systems， 1996， 10（2）：109-129.

[14] ZHANG B， YUAN S Q， ZHANG J S， et al. Study of Corn Optimization Irrigation Model by Genetic Algorithms[J].Computer and Computing Technologies in Agriculture，1969，1：121-132.

[15] 潘琦，夏爽，郭珊珊，等.基于渠系輸水模拟与土壤水量平衡模拟的两级渠系优化配水模型[J].中国农业大学学报，2020，25（5）：151-162.

[16] 郭元裕.农田水利学[M].3版.北京：中国水利水电出版社，1997：29-51.

[17] WANG Y Z， LIU L， GUO P， et al. An Inexact Irrigation Water Allocation Optimization Model Under Future Climate Change[J]. Stochastic Environmental Research and Risk Assessment， 2019， 33：271-285.

[18] 杜斌.渠村灌区水资源多目标优化配置研究[D].北京：华北电力大学，2017：47-70.

[19] 何胜. 冬小麦适应性节水灌溉预报与实时配水技术研究[D].郑州：华北水利水电大学，2016：23-27.

[20] 张会茹.华北地区冬小麦需水量及节水灌溉分析探讨[J].河北水利，2010（4）：28.

【责任编辑 许立新】