复杂构型水下机器人水动力导数及运动性能预报

褚洪贵， 王志东， 凌宏杰

(江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003)

0 引 言

近年来，海底沉船搜寻与设备打捞、石油钻井平台安装与维护、水库大坝的监视与检测，石油管道的敷设与喷漆、水下设施的清洗与重新涂装等作业量日益增长，随着科学技术迅速发展，水下机器人展现在大众视野，得到了广泛应用。为实现机器人在深水空间达到预期设计目标任务，必须准确获取水动力系数，确保其具有良好的操纵性能[1-3]。本文对复杂构型开架式带缆遥控水下机器人(Remote Operated Vehicle，ROV)进行水动力数值模拟研究。

随着计算机和计算流体的发展，低成本、快速的数值模拟成为水动力求解的主要方式。张风丽[4]基于计算流体动力学(Computational Fluid Dynamics，CFD)技术求解雷诺时均N-S(Reynolds-Averaged Navier-Stokes，RANS)方程，数值模拟SUBOFF模型的拘束模试验，得到精度较高的惯性水动力导数，可作为潜艇水动力导数数值预报方法。海燕[5]对轻载载人水下机器人(Human Occupied Vehicle，HOV)斜航及不同频率、振幅下的纯升沉和纯俯仰运动进行水动力性能数值计算。漆小舟等[6]基于OpenFOAM软件对万米自主遥控水下机器人(Autonomous and Remotely Operated Vehicle，ARV)在不同漂角和攻角下进行数值斜航试验，计算得到ARV的水动力(矩)，回归得到水动力导数。

虽然相关学者[7-10]建立潜体数学模型并对水动力导数进行求解，但是对结构复杂且存在多体干扰的开架式水下机器人水动力导数求解甚少。张燕等[11]以形状复杂的开架式有缆水下机器人作为研究对象，通过一系列水动力试验，计算出适用于开架式水下机器人模型的几个重要的实时水动力系数。陈英龙等[12]为测量低速域水下遥控机器人水动力系数，设计一套水下遥控机器人水动力试验系统。ALLOTTA等[13]在研发台风级水下机器人工作中提出水动力参数的辨识对于精确的动力学模型的整定非常重要，可用于模型的定位和导航滤波器的开发。戴君锐等[14]采用格特勒标准六自由度运动方程，通过水池拖曳试验获取水动力系数，建立水下航行器运动模型，对水下航行器样机操纵性和运动控制性能进行预报。

本文以复杂多体开架式ROV为研究对象，基于MMG(Maneuvering Modeling Group)操纵性运动方程分离思想[15]，建立ROV四自由度运动数学模型。采用CFD方法对直航、纯升沉、纯横荡、纯纵荡和纯艏摇进行水动力数值计算，并将获取的水动力导数代入数学模型中进行运动仿真，在给定螺旋桨推进器转速下，得到回转运动仿真曲线与3个主轴方向加速度、速度和位移的时历曲线。

1 数值计算模型

在讨论ROV的运动学问题之前，须先确立适合描述其运动的数学坐标系。采用随体坐标系，亦称为运动坐标系：其原点与ROV的重心重合；Ox轴与ROV的主对称轴一致，运动方向为正向；Oy轴平行于基线面并垂直于Ox轴，指向ROV本体右侧为正；Oz轴位于ROV主体中纵剖面内，与Ox、Oy轴垂直，指向顶部为正[16]。

开架式ROV外形基本尺寸为0.80 m×0.41 m×0.37 m，因此计算域选择形状为5.00 m×3.00 m×2.80 m的长方体，前方边界距ROV本体1.65 m。开架式ROV零件众多，结构体比较复杂，细小的间隙和尖角难以分布网格。因此，在不改变ROV整体结构形式的条件下，适当修改或者去除某些对水动力性能计算影响较小的部分，ROV简化模型如图1(a)所示。网格整体遵循非结构化、局部加密的原则。由于非结构化是适应性较好的网格形式，可适应各种形状复杂的求解域，经过适当优化，网格单元数约300万，网格划分如图1(b)所示。

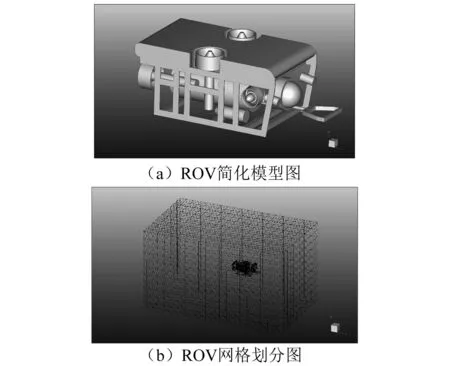
图1 ROV数值计算模型

2 数学模型

假设该ROV重力等于浮力，本体结构可近似认为左右对称、上下非对称体。根据MMG操纵性运动方程和动力分布状态，在不计及波浪、流的影响，静水条件下，只考虑纯升沉、纯横荡、纯艏摇和纯纵荡等4种运动模态下一阶水动力导数，建立ROV水动力方程为

(1)

(2)

(3)

(4)

3 数值计算方法

采用的数值计算方法包括直航运动和CFD仿真模拟平面运动机构(Planar Motion Mechanism，PMM)试验。PMM试验通过测量ROV本体模型在不同运动模态下海水中所受到的水动力和力矩，基于MATLAB软件平台编写出水动力系数提取程序，进而确定ROV操纵运动所需的各种加速度导数和速度导数。由于仅测定线性水动力系数，因此PMM试验采用小振幅模拟试验，主要模拟模态包含以下几种运动形式：纯升沉运动、纯横荡运动、纯纵荡运动、纯艏摇运动。

3.1 直航运动

直航阻力试验是测定试验模型在不同流速下所受到的纵向阻力，由测得的流速(V)-阻力(F)曲线就可以确定模型的直航阻力系数。本试验通过模拟ROV在0.3～1.5 m/s的直航运动阻力F求解阻力系数Xuu。表1为不同航速下的直航运动阻力。利用最小二乘法进行曲线拟合，拟合曲线如图2所示。

表1 不同航速下直航运动阻力

图2 直航阻力拟合曲线

求得阻力系数Xuu=0.162 9。

3.2 纯升沉运动

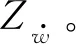
(5)

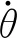
由纯升沉运动方程得

(6)

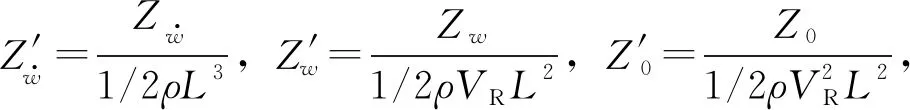
图3 T=5 s时纯升沉水动力导数辨识曲线

表2 不同时间周期纯升沉水动力导数

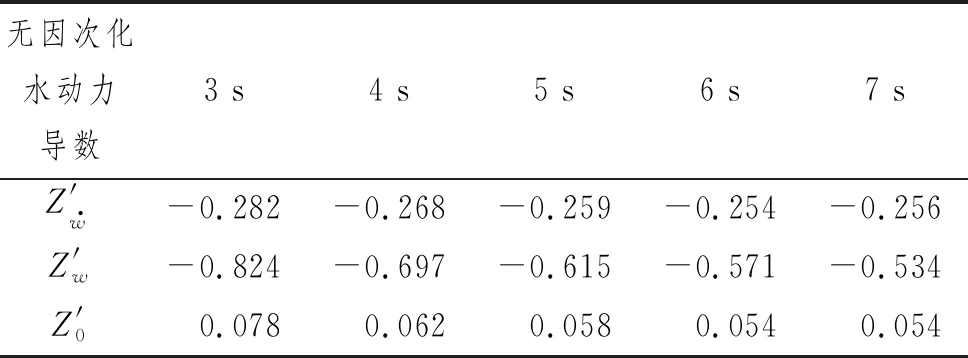
表3 不同时间周期纯升沉水动力导数无因次化

3.3 纯横荡运动

(7)

可得到ROV纯横荡运动方程为

(8)

(9)

图4 T=5 s时纯横荡水动力导数辨识曲线

表4 不同时间周期纯横荡水动力导数

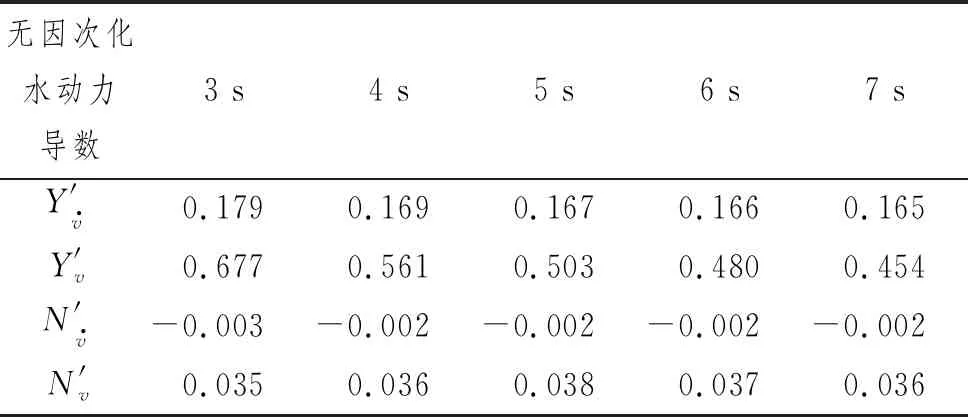
表5 不同时间周期纯横荡水动力导数无因次化

3.4 纯艏摇运动

(10)

(11)

(12)

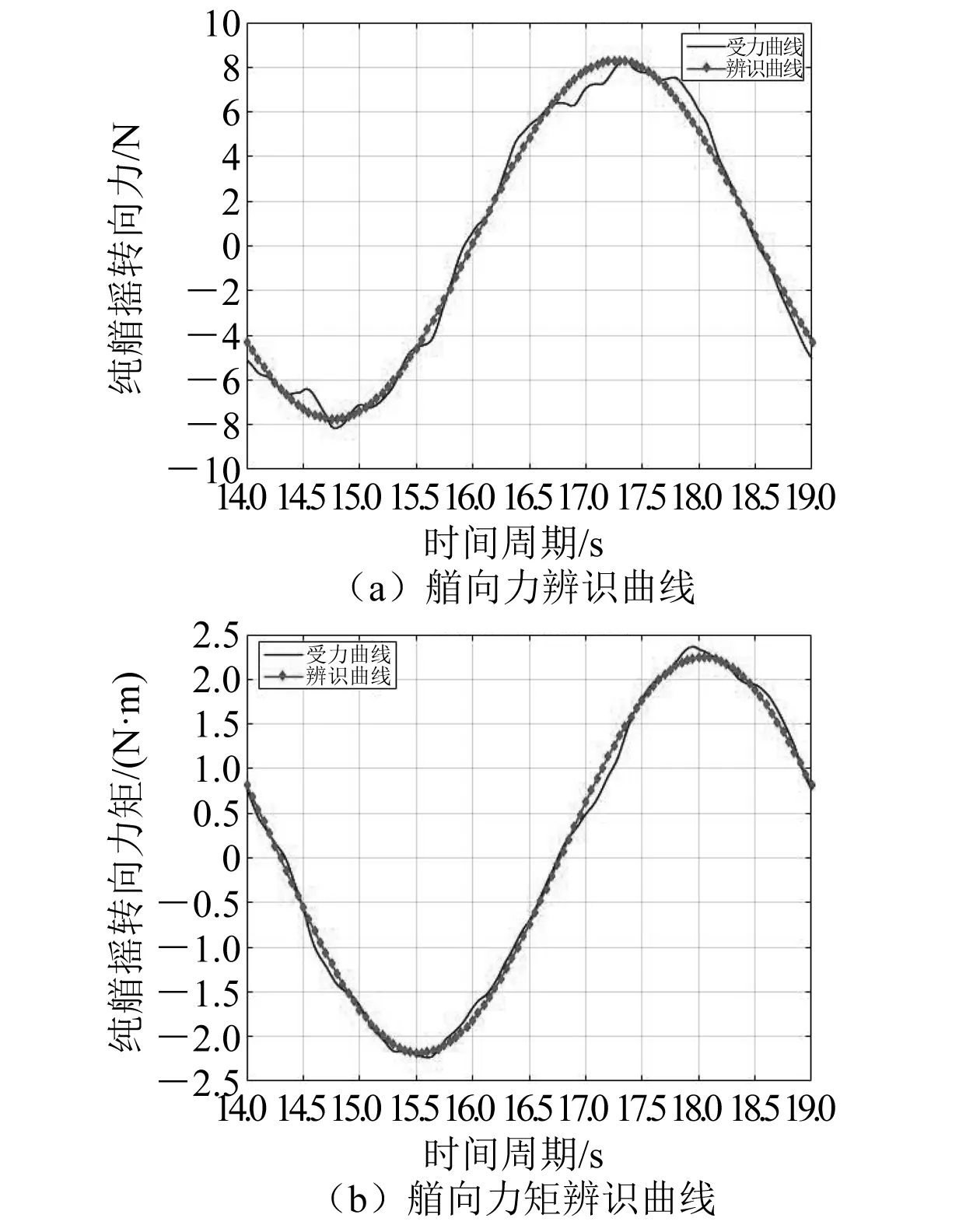
图5 T=5 s时纯艏摇水动力导数辨识曲线

表6 不同时间周期纯艏摇水动力导数

表7 不同时间周期纯艏摇水动力导数无因次化

3.5 纯纵荡运动

(13)

式中：η为ROV的纵向位移。

可得到ROV纯纵荡方程为

(14)

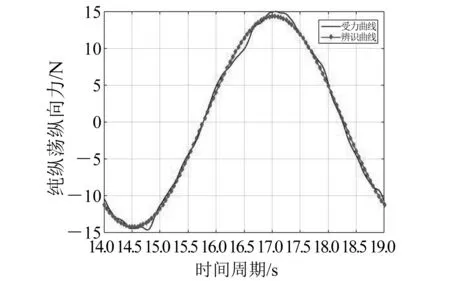
图6 T=5 s时纯纵荡水动力导数辨识曲线

表8 不同时间周期纯纵荡水动力导数

表9 不同时间周期纯纵荡水动力导数无因次化

4 运动仿真模拟

以MATLAB作为编程工具构建ROV运动仿真平台，将辨识出的速度水动力系数与加速度水动力系数代入四自由度运动数学模型，进行运动仿真模拟。

该ROV共有5个螺旋桨推进器，其定义Ox正向(前进方向)左侧水平螺旋桨推进器为n1,Ox正向(前进方向)右侧水平螺旋桨推进器为n2，竖直左侧螺旋桨推进器为n3, 竖直右侧螺旋桨推进器为n4，侧向螺旋桨推进器为n5。假定回转仿真试验转速R如下：Rn1=20 r/s、Rn2=-10 r/s、Rn3=Rn4=-20 r/s、Rn5=30 r/s。

图7为设定运动时长ts=180 s时，ROV回转运动轨迹。结果表明该ROV可实现原地回转，在假定条件下，回转半径约40 m，回转速度约2.9 m/s。

图7 回转仿真结果

5 结 论

基于FINE/Marine软件平台，针对复杂开架式ROV，开展PMM运动数值模拟，求解其在低速、小振幅运动状态下纯升沉、纯横荡、纯艏摇和纯纵荡等4种运动模态、5个不同时间周期的水动力与力矩，使用MATLAB软件辨识ROV的水动力导数。完成四自由度ROV运动仿真平台的搭建，并将CFD数值计算求得的水动力导数代入运动数学模型，可实现ROV原地回转，为开架式ROV操纵水动力导数的获取提供了一种有效计算方法。求解的水动力导数为水下复杂构型ROV操纵性仿真预报奠定了可靠的基础。