基于空间降维和多核支持向量机的网络入侵检测
田桂丰,单志龙,廖祝华,王煜林
(1.广州理工学院 计算机科学与工程学院,广东 广州 510540;2.华南师范大学 计算机学院,广东 广州 510631;3.湖南科技大学 计算机科学与工程学院,湖南 湘潭 411103)
随着互联网的高速发展,接入网络的节点数不断增加,网络服务也随之逐渐增多,特别是金融、社交和电商类服务的增加,安全问题成为网络服务需要大力发展的基础保障[1]。网络入侵检测能够有效发现网络中的隐藏攻击,并能分辨出攻击类型,从而为网络安全决策提供有力保障。对于网络数据包的安全检查,可以采用安全规则匹配的方式来完成;但是无法满足大规模数据和实时性高的网络入侵检测要求,因此更高效的入侵检测算法成为入侵检测技术的研究热点。
近年来,关于网络入侵检测技术的研究较多,张宝华等[2]采用支持向量机(support vector machine,SVM)与遗传算法相结合的模式进行网络入侵检测,改善了SVM算法的迭代效率,降低了网络入侵的检测时间,但检出率并不高。陈红松等[3]采用循环神经网络方法用于无线网络的网络入侵检测,通过多次训练有效提高了网络攻击检出准确度,但也带来了较大的虚警报率。夏景明等[4]采用仿生算法与深度置信网络结合方法进行大规模网络入侵检测,表现出了良好的网络入侵检测率,但检测时间较长。在这些研究中,有的算法虽然网络入侵检出率较高,但存在检测效率不高的问题。部分算法的网络入侵检出率高,但误报率也高,需要不断优化入侵检测算法。针对上述问题,本文中将多核SVM算法应用于网络入侵检测,并且采用局部线性嵌入(locally linear embedding,LLE)进行数据降维,从而能够获得较好的网络入侵检出率,并且提高检测效率。
1 网络入侵检测模型
网络入侵检测主要是根据网络中传输的数据包是否正常,通过安全规则分析数据包是普通数据还是攻击数据,对攻击数据进行相应的安全处理。检测模型[5-6]如图1所示。

图1 网络入侵检测模型
在事件数据库中,制定安全规则和策略,通过规则匹配与规则分析,判断当前网络事件是否为正常数据包,根据事件类型执行规定动作,从而完成网络入侵检测。在事件分析过程中,首先要分辨正常数据包和入侵数据包,其次要通过分类算法对入侵数据包按攻击类型进行分类,统计分析分类结果并有针对性地制定相应的网络安全防御系统。
网络入侵主要攻击类型有DOS、Probe、R2L和U2R[7],这4种类型还可以进一步划分为更多小类,在分析过程中,可以根据实际情况选择分类粒度,然后制定分类策略。本文中只选择这4种常见攻击类型作为分类对象。
2 多核SVM和空间降维
2.1 SVM
SVM能够使用一条线将混合在同一空间的数据分开,并且最大限度地维持较大的分类间隔。
设分类线为
wx+b=0,
(1)
式中:w为斜率;x为数据点;b为截距。
对于二元分类,y∈{-1,1},m个样本集满足以下条件:
yi(wxi+b)-1≥0,i=1,2,…,m。
(2)
式中yi为样本i的类别。

(3)

上述求解过程的约束条件为
(4)
分类函数[9]为
(5)
式中sgn(·)为阶跃函数。
2.2 核函数理论
设X是一个n的一个子集,连续函数K满足条件[10]

(6)
式中:x′为不同于x的变量;f(x)是实函数且满足条件
(7)
则有
(8)
式中λi(≥0)和φi(x)分别是积分算子特征值和特征函数,其中特征函数的特征解为
(9)
在当前的多核函数研究中,常见的核函数[11]有以下3种。
1)高斯核函数,
(10)
式中σ为控制函数作用范围的常量。
2)多项式核函数,
K(x,y)=(〈x·y〉+R)d,R≥0,d≥0 ,
(11)
式中:R为人工设置的常量;〈x·y〉为由x和y组成的多项式。
3)Sigmoid核函数,
K(x,y)=tanh(g〈x·y〉+R),g>0,R≥0 ,
(12)
式中:tanh(·)为Sigmoid函数;g为系数常量。
采用多核函数的主要原因是单核函数分类效果不理想,与输入空间大小有很大关系。通常按照输入向量服从的分布来选取合适的核函数,如果输入数据源多样或者分布多样,可以选择多个核函数融合的方法来完成分类。
2.3 LLE降维
设样本xi可以由其相邻样本xj、xk和xl(k,l=1,2,…,m)经过线性运算[12]得到,
xi=ωijxj+ωikxk+ωilxl,
(13)
式中ωij、ωik和ωil分别为样本xi与其相邻样本xj、xk和xl的线性系数。
在实际操作过程中,xi的相邻样本可以选择多个,设xi的k个邻居样本组成的集合为Qi,为了保持降维后样本点仍属以前的线性关系,LLE的降维目标函数[13]为
(14)
设Cjk=(xi-xj)T(xi-xk),则
(15)
LLE能够保持降维过程中ωij不变,所以根据ωij,可以求解降维后的样本集合,
(16)

通过求解ωij的特征值所对应的特征向量则可以得到降维后的Z。
2.4 网络入侵检测流程
采用LLE对抓取的网络数据进行降维处理,然后对降维后的数据采用多核SVM方法进行数据包检测,在多核函数选取时,考虑2种或者2种以上核函数混合的方式来进行SVM计算。算法流程如图2所示。

图2 基于空间降维和多核支持向量机(SVM)的网络入侵检测算法流程
3 实例仿真
为了验证空间降维和多核SVM的网络入侵检测效果,进行实例仿真。仿真数据来源如下:Lincoln实验室的KDD cup99数据(数据集1),网络入侵样本个数为494 021,网络正常数据和入侵数据样本个数分别为97 278和396 743;HTTP DATASET CSIC 2010数据集(数据集2),样本个数为50 021;Masquerading User Data 数据集(数据集3),样本个数为14 872;澳大利亚ADFA IDS Datasets数据集(数据集4),样本个数为32 841。数据集中训练样本个数与测试样本个数比例为3∶1。差异化设置LLE降维参与运算的邻节点个数,采用多核函数混合方法,充分验证基于空间数据降维和多核SVM算法(简称本文算法)对网络入侵检测性能的影响,最后比较本文算法与常用的网络入侵检测算法在不同数据集的性能差异。
3.1 数据降维性能
为了验证LLE在网络入侵检测中的性能,对数据集3采用MATLAB软件进行仿真,其训练样本属性初始分布如图3所示。

图3 训练样本初始分布
分别选择不同邻居数N进行LLE线性表示,然后坐标转换降维,差异化设置N分别为10、20、30、50,其中N为10、20时的降维效果如图4所示。
对比图4(a)、(b)发现:N=10的LLE数据降维效果并不理想,很多节点仍有交叉重叠,二维分布不能完全展示样本属性;当N=20时,数据样本平铺展开完整,较好地实现了三维到二维的降维处理。

(a)N=10
不同邻居数N的LLE网络入侵检测性能如表1所示。从表中数据可以看出:邻居数为10时,4个数据集样本的检出率均低于90%;随着邻居数增加到20,检出率缓慢提高,表明当邻居节点数较少时,LLE的降维作用不大,对网络入侵检测的帮助较小。而当节点数超过20后,LLE降维相邻节点参与运算的数量变化对网络入侵检出率影响逐渐变小,但是检测时间显著增加,其原因是更多节点参与空间降维的运算复杂度增大,导致检测用时增加。

表1 不同邻居数N的局部线性嵌入网络入侵检测性能
3.2 不同多核SVM的网络入侵检测性能
选取LLE参与计算的邻居数为20,对高斯核函数、多项式核函数和Sigmoid核函数分别两两混合,采用混合核函数SVM对网络入侵方式进行检测,结果见表2。由表可以看出:对于数据集1、2、3,核函数的组合方式不同,网络入侵的检出率差异较大,这是由样本的分布构成决定的;数据集4的网络入侵检出率受核函数组合的影响不大,检出率均在0.973以上。在检测时间方面,多核函数组合模式并没有对检测时间性能造成大的影响,通过4个数据集样本检测时间的横向对比可以看出,检测时间与样本量呈正比的关系,样本量最少的数据集4检测时间最短。综合而言,对于不同的数据集,为了获得最优的网络入侵检测效果,应采取合适的核函数组合方式。
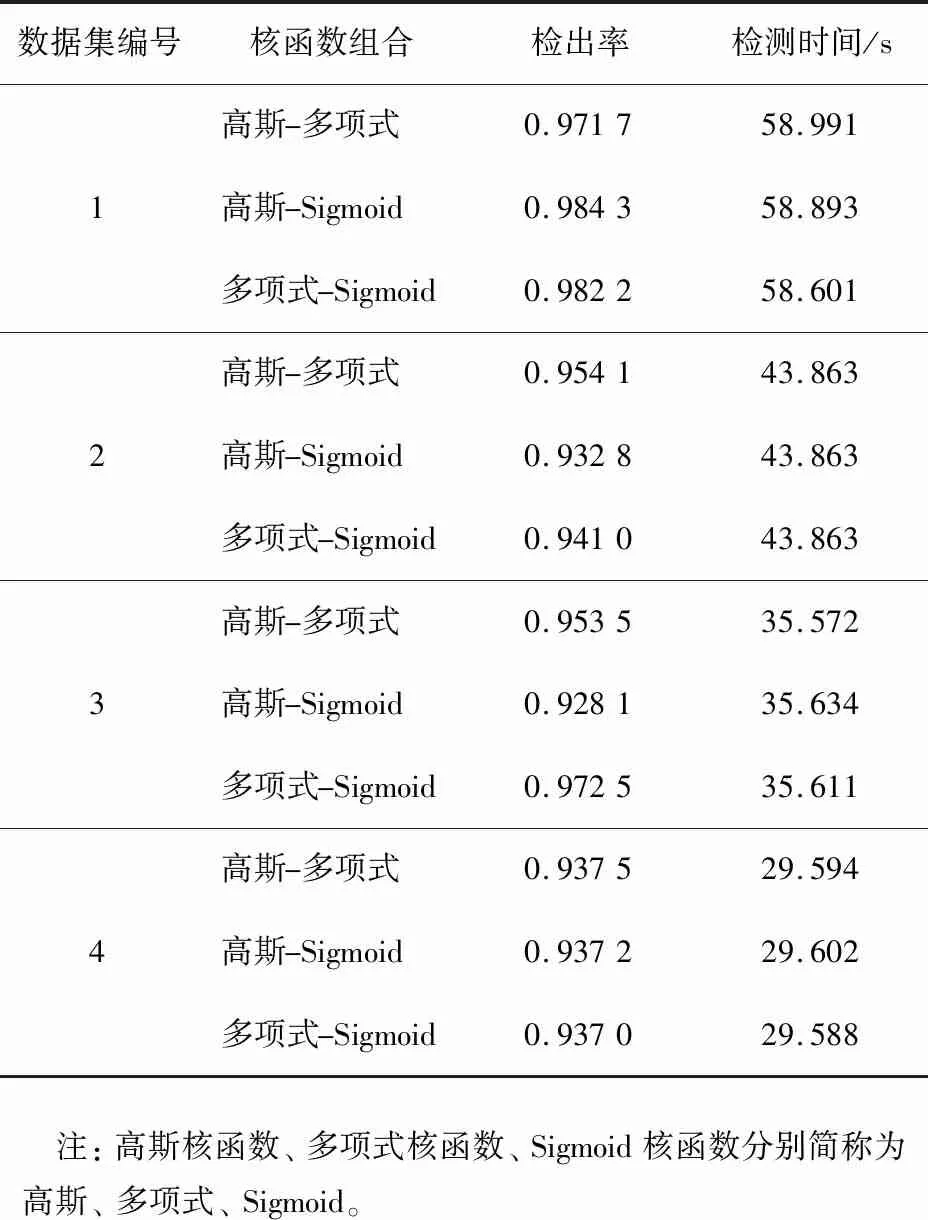
表2 不同多核支持向量机的检测性能
3.3 不同算法性能对比
为了验证不同网络入侵检测算法的网络攻击检出性能,分别采用K近邻(KNN)-SVM[14]、粒子群算法(PSO)-SVM[15]、卷积神经网络[16]和本文算法对数据集1分别进行性能仿真。本文算法采用LLE邻居数为20,多核函数采用高斯核函数与Sigmoid核函数组合的方式,仿真结果如图5所示。由图可以看出,本文算法和卷积神经网络算法的检出率最高,数值非常接近,KNN-SVM的检出率最低。对比检测时间,KNN-SVM和PSO-SVM在50 s之前均已完成检测,而本文算法在60 s左右才完成收敛,卷积神经网络检测时间最长,大约需要70 s。综合对比检出率和检测时间,本文算法的网络入侵检测率高,耗时较短。

KNN—K邻近算法;SVM—支持向量机;PSO—粒子群算法;LLE—局部线性嵌入。图5 不同算法的网络入侵检测性能
4 结语
本文中采用LLE空间数据降维和多核SVM算法用于网络入侵检测,通过合理设置LLE计算的邻居数,灵活选择核函数的混合方法,可以获得较高的网络入侵检出率。后续研究将进一步优化核函数组合模式及多核函数的选择,以进一步优化网络入侵检测性能。

