基于小波规则的燃料电池电动汽车能量管理策略
王永军,孙宾宾,李文涛,高 松,颜敬昊,魏 国
(山东理工大学 交通与车辆工程学院,山东 淄博 255049)
燃料电池电动汽车(FCEV)以清洁无污染、零排放、能量转换效率高等优势成为新能源汽车领域研究的热点;但是,由于燃料电池动态响应缓慢,并且作为单向输出能源不能进行制动能量回收,因此为了满足整车动力性以及经济性要求,FCEV多以燃料电池为主要动力源,其他辅助储能动力能源如动力电池、超级电容和飞轮储能装置等进行搭配使用。
采用复合能源系统的方案可以实现对负载需求功率的有效分流控制。FCEV能量管理策略的核心问题是如何将整车需求功率合理分配给各能量源,保证燃料电池稳定高效工作,从而延长燃料电池的使用寿命[1]。
目前车辆能量管理策略主要分为基于规则和基于优化2个研究方向[2]。张梦等[3]将基于模糊控制和基于状态的自适应功率控制策略进行仿真对比,验证了模糊逻辑控制策略具有减少H2消耗量、增加续航里程的优越性。聂彦鑫等[4]从工程实际出发,采用基于规则的能量管理策略,通过控制燃料电池系统与蓄电池之间的功率分配,使燃料电池系统始终工作在高效率区域,以获得整车最佳燃料经济性。郭朋彦等[5]通过功率跟随控制策略仿真模拟,研究了该策略对燃料电池混合动力汽车(FCHV)动力性和经济性的影响。以上能量管理策略的研究虽然取得了一定的效果,但是从燃料电池动态响应较慢的角度分析,以上控制策略并没有很好地抑制燃料电池频繁波动的需求功率以及峰值功率的输出。
本文中从实际工程角度出发,通过分析不同机理对燃料电池使用寿命的影响,正向制定相应的适合燃料电池复合能源系统的小波规则二级功率分流能量管理策略,在满足整车动力性的前提下,抑制燃料电池高频变化的峰值功率的输出,使燃料电池始终工作在高效区间,从而达到延长燃料电池使用寿命的目的。
1 FCEV复合能源系统设计
1.1 复合能源系统结构
本文中研究的燃料电池复合能源系统采用半主动拓扑结构[6],主要由燃料电池、蓄电池、单向DC(直流电)/DC转换器、驱动电机及其整车控制器(VCU)等组成,如图1所示。燃料电池通过单向DC/DC控制器与蓄电池并联组成复合能源系统;燃料电池由空气压缩机、冷凝器、增湿器、减压阀、燃料电池堆冷却系统等辅助器件组成;蓄电池组是由单体电池采用串并联的方式组成动力电池组。
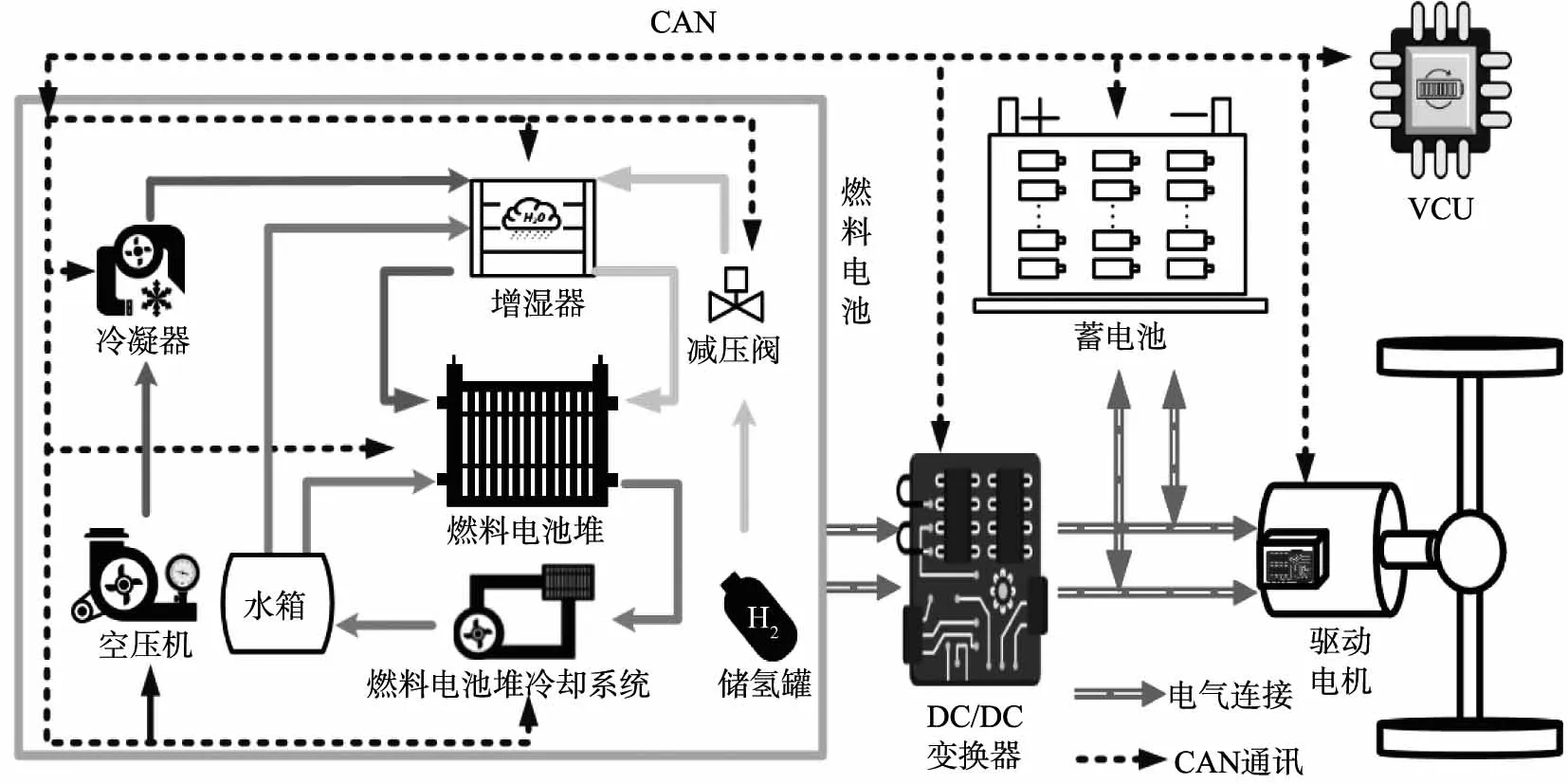
CAN—总线协议;DC—直流电;VCU—整车控制器。图1 燃料电池电动汽车复合能源系统结构
1.2 燃料电池模型
燃料电池模型根据稳定模型[7]进行建立,其中,单体燃料电池堆稳态模型输出端电压Ufc为
Ufc=ENernst-Uact-Uohm-Uconc,
(1)
式中:ENernst为热力学电动势;Uact为活化过电压;Uohm为欧姆过电压;Uconc为浓差过电压。
根据Nernst方程,热力学电动势ENernst为
ENernst=1.229-8.5×10-4(Tst-298)+
(2)
式中:Tst为燃料电池堆温度;PH2为燃料电池堆内部H2分压;PO2为燃料电池堆内部O2分压。
(3)
Uohm=iRohm,
(4)
(5)
式中:R为气体常数;α为电荷转移系数;F为法拉第常数;i、i0分别为催化剂单位表面积上的电流密度、交换电流密度;Rohm为欧姆电阻;C为质量转移系数;ilim为电流极限密度。
1.3 锂动力电池模型
锂动力电池输出功率变化的时间常数远小于燃料电池的,借助锂动力电池作为辅助能源来响应需求功率的剧烈变化,减少燃料电池负载波动和开关启动次数,延长燃料电池的使用寿命。常见的电池模型主要有等效电路Rint模型(Rint为等效电阻)、Thevenin模型及新一代汽车合作计划(PNGV)模型等[8]。本文中采用常用的等效电路Rint模型对锂动力电池组进行建模,等效电路Rint模型如图2所示。
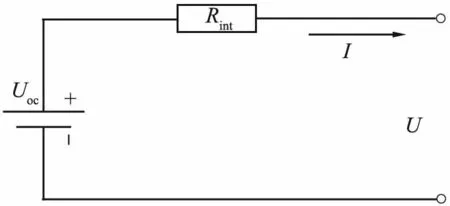
Uoc—开路电压;Rint—等效电阻;I—锂动力电池电流;U—锂动力电池端电压。图2 锂动力电池的等效电路等效电阻模型
锂动力电池的开路电压Uoc和等效电阻Rint是锂动力电池温度T、荷电状态(SOC)QSOC的函数[9],即
Uoc=f(T,QSOC),
(6)
Rint=f(T,QSOC)。
(7)
锂动力电池端电压U为
U=Uoc-IRint,
(8)
式中I为锂动力电池电流。
根据锂动力电池的需求功率,计算得到
(9)
式中Pbat为锂动力电池输出功率。
锂动力电池SOC为
(10)
式中:Qmax为锂动力电池最大容量;t为电流流经时间。
2 能量管理控制策略推导
2.1 影响燃料电池寿命的机理
不同于燃油发动机,燃料电池是一种通过电化学反应,把燃料化学能中的吉布斯自由能转换成电能,不受卡诺循环效应限制的发电装置[10]。燃料电池工作时需要一定的启动时间,复杂多变的行驶工况很容易影响燃料电池的使用寿命,主要分为4种工况,即启停工况、剧烈变载工况、怠速工况、过载工况。4种工况影响燃料电池寿命的机理如图3所示。
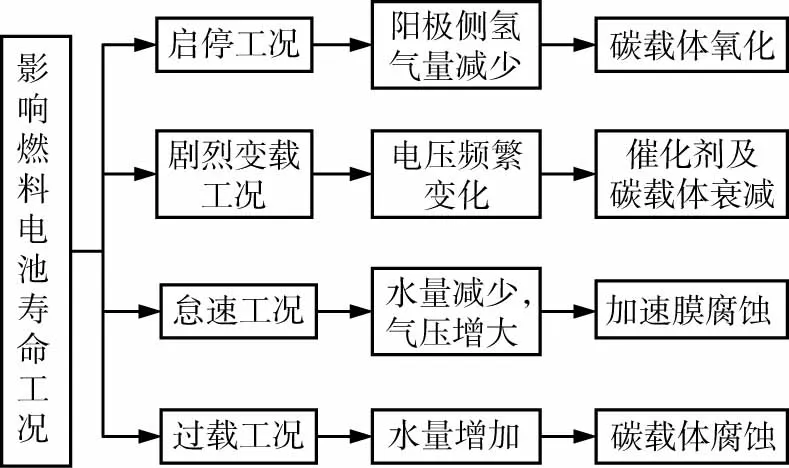
图3 4种工况影响燃料电池寿命的机理
根据影响燃料电池寿命的机理,在设计能量管理策略时,应尽量避免燃料电池在这些工况中工作。小波变换具有较好的时频分辨率,可以提取瞬态信号[11],使负载需求功率中的高频功率分量和低频功率分量进行解耦,这样可通过小波变换的解耦特性实现一级功率分流,初步获得适用于燃料电池的瞬态功率变化缓慢的低频功率信号。
2.2 工作模式分析
根据燃料电池、锂动力电池工作特性,为了进一步使燃料电池获得稳定的功率信号,划分4种工作模式,如图4所示。
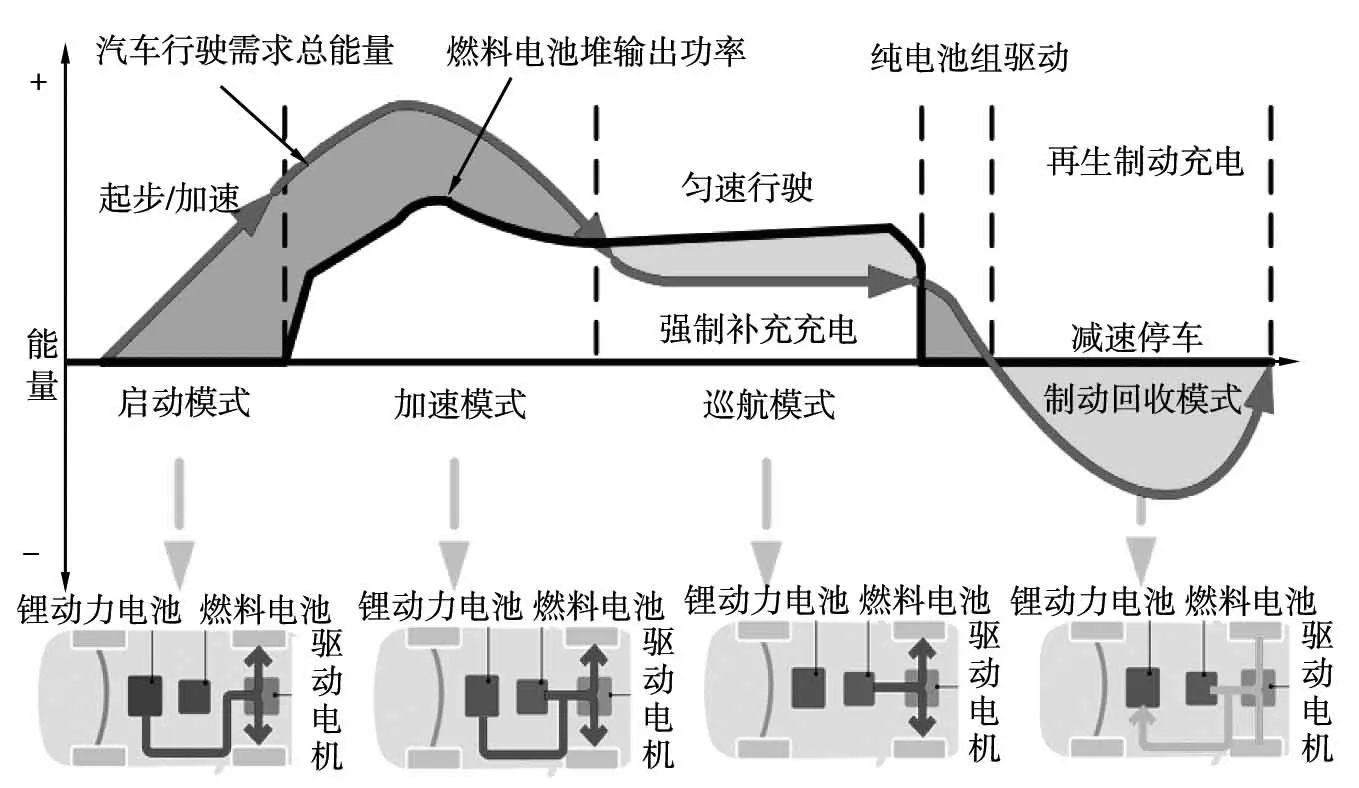
图4 燃料电池电动汽车能量流动对应的4种工作模式
1)启动模式。燃料电池从启动到对外做功,需要一些必要的准备,此时由锂动力电池平稳地启动车辆。整车需求功率Pre决定是否启动燃料电池系统,如果这时需求功率Pre小于燃料电池系统高效工作区的最小允许输出功率PFC,min,则锂动力电池仍单独驱动。
2)加速模式。汽车加速或上坡时,燃料电池系统高效工作区的最大允许输出功率为PFC,max,锂动力电池对整车需求功率Pre进行补充,锂动力电池在此起到功率补充的作用,即联合驱动模式。
3)巡航模式。此时需求功率Pre平稳,如果电池SOC小于设定的最小值QSOC,min,燃料电池驱动车辆的同时为锂动力电池充电使其SOC维持在目标值附近。如果锂动力电池SOC在正常范围,则尽量让燃料电池工作在高效点,不足或多余的部分由锂动力电池补充或回收。
4)制动回收模式。当汽车减速或者制动时,在低制动功率条件下,锂动力电池尽量吸收全部再生制动能量;在高制动功率条件下,为了防止锂动力电池出现过充现象,即电池SOC大于设定的最大值QSOC,max,锂动力电池只回收低制动功率条件下的低频部分。只有当再生制动达到最大制动能力,但是还不能满足制动要求时,机械制动才起作用。
3 小波规则二级功率分流策略
小波变换能够将原始信号分解成不同位移和尺度的分量,具有局部化的属性,非常适合分析非周期、非稳定的暂态功率信号[12]。尤其对于城市工况下的FCEV,小波变换在分解频繁变化的暂态功率方面具有显著优势。
3.1 Haar小波的双通道正交滤波器组设计
Haar小波是唯一具有对称性的正交紧支撑小波,并且Haar小波滤波器滤波长度最短[13],使用Haar小波进行小波分解与重构,可以简化小波算法程序,提高代码执行率。以小波φ(t)为母函数,构造正交空间WJ、VJ(J为信号分解层数),燃料电池总需求功率Pre∈VJ-1,WJ-1为VJ-1对于VJ的正交补空间[14],通过定义滤波器系数wJ-1(t)∈WJ-1,可以得到
(11)
式中:PbJ(t)为离散输入信号;l为离散化的平移因子;al、bl为离散化的尺度因子;信号分解层数J取为3。 结合式(11)和Haar小波函数,设计滤波器组为
(H0(z)h1(z)G0(z)G1(z))T=
(12)
式中:z为多相变换域;H0(z)、H1(z)分别为分解高、低通离散滤波器;G0(z)、G1(z)分别为重构高、低通滤波器[15];b1—b8为滤波器状态参数。
整车需求功率信号Pre实现一级功率分流,被分解为高频需求功率信号Psup和低频需求功率信号Pinf。功率解耦过程如图5所示。
需求功率Pre(t)分流后的表达式为
(13)
式中:x0(t)为t时刻第3阶低频分量;x1(t)、x2(t)、x3(t)分别为t时刻第1、2、3阶高频分量。
3.2 基于小波规则的能量管理策略
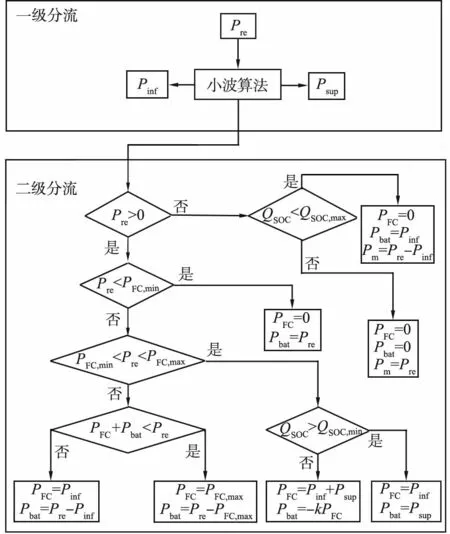
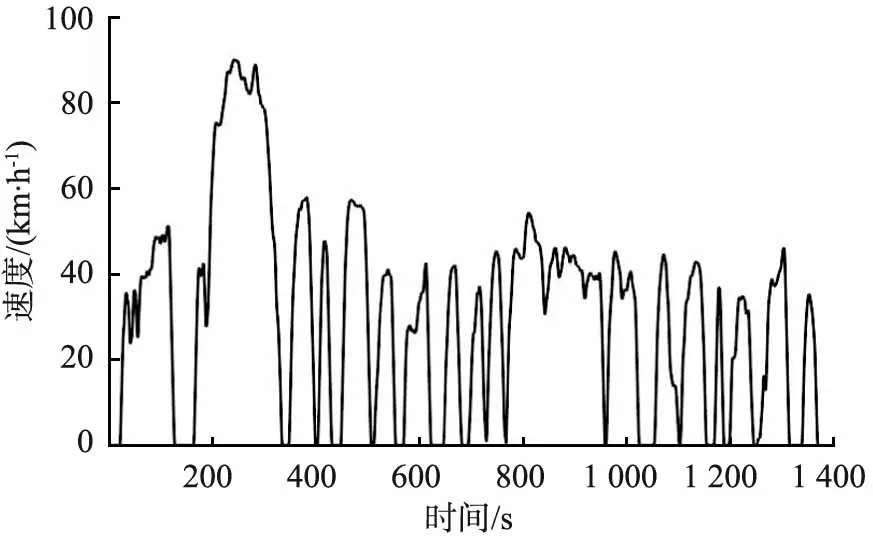
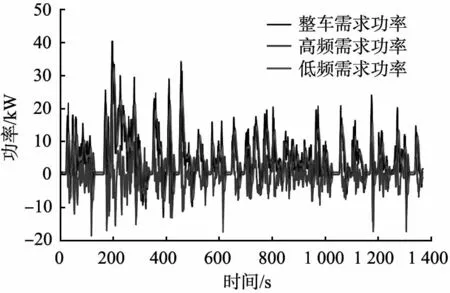
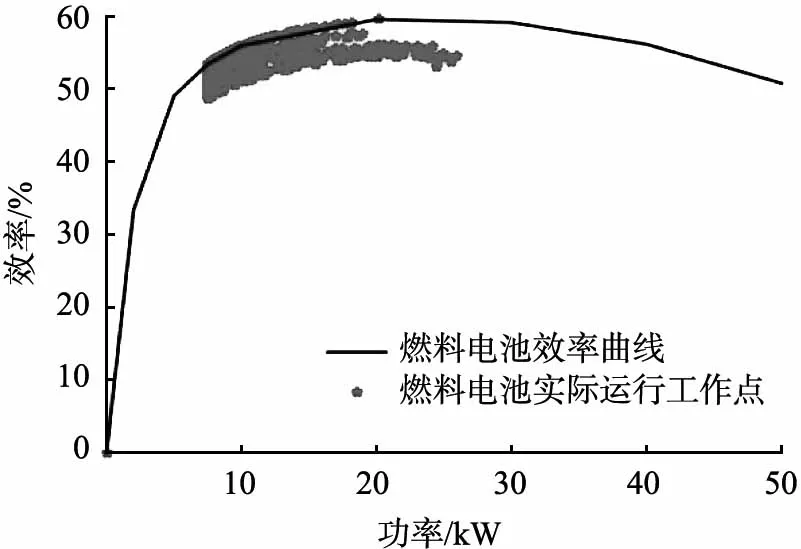
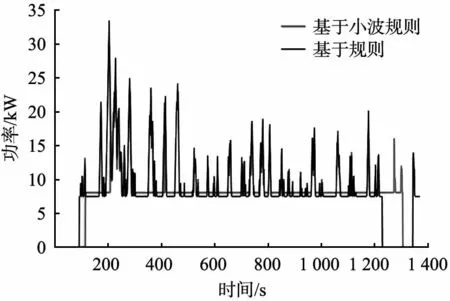
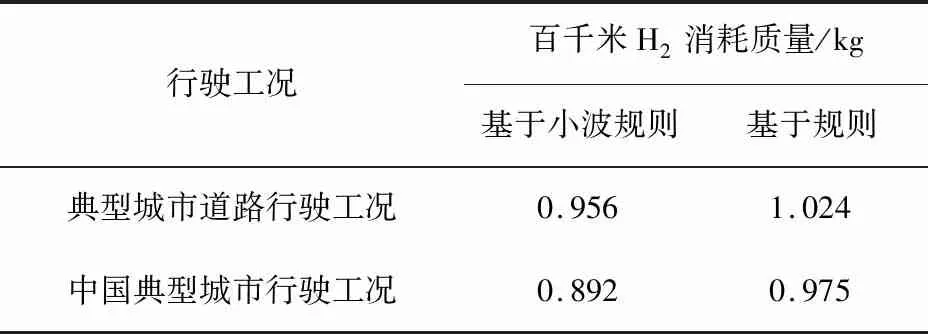
根据小波变换原理,基于MATLAB软件对3阶Haar小波进行编程,保存为M文件以备调用,最后基于Simulink软件进行小波规则建模。图6所示为基于小波规则二级功率分流的能量管理策略流程,其中Pre>0表示驱动模式,Pre<0表示制动模式,k为常数,0 x(t)—t时刻的输入信号;x0(t)—t时刻第3阶低频分量;x1(t)、x2(t)、x3(t)—t时刻第1、2、3阶高频分量;y(t)—重构后的输出信号;H0(z)、H1(z)—分解高、低通离散滤波器;G0(z)、G1(z)—重构高、低通滤波器;↓2—下采样算子;↑2—上采样算子。图5 3阶Harr小波功率解耦过程 Pre—整车需求功率;Psup—高频需求功率;Pinf—低频需求功率;QSOC—锂动力电池荷电状态;QSOC,min、QSOC,max—锂动力电池荷电状态下限值、上限值;PFC—燃料电池输出功率;PFC,min、PFC,max—燃料电池系统高效工作区的最小、最大允许输出功率;Pbat—锂动力电池输出功率;Pm—机械制动功率;k—常数。图6 基于小波规则二级功率分流的能量管理策略流程 根据已完成的小波规则二级功率的分流能量管理策略,借助Simulink仿真平台对FCEV整车模型进行仿真,以典型城市道路行驶工况为仿真工况,验证该策略中小波一级功率分流的可行性。典型城市道路行驶工况及对应的功率如图7所示。 (a)典型城市道路行驶工况 图8所示为整车需求功率解耦曲线。从图中可以看出,根据小波变换原理,FCEV整车需求功率实现了一级功率分流,需求功率Pre被分解为高频需求功率Psup和稳态低频需求功率Pinf。 图8 整车需求功率解耦曲线 图9所示为燃料电池实际运行工作点曲线。从图中可看出,在基于小波规则的控制策略下,燃料电池效率值主要保持在50%~60%,说明该策略能够保证燃料电池工作在高效区间,能达到延长燃料电池寿命的目的。 图9 燃料电池实际运行工作点曲线 图10(a)所示为在基于小波规则和基于规则2种策略下燃料电池输出功率变化。由图可知,在基于小波规则的控制策略下,燃料电池峰值输出功率曲线波动频率小于基于规则的控制策略的,其中基于规则的控制策略的最大峰值功率为34.26 kW,而基于小波规则的控制策略的最大峰值功率不超过24.64 kW,表明该策略能抑制燃料电池峰值功率的输出。 图10(b)所示为不同策略下锂动力电池输出功率变化。从图中可看出,在驱动条件下,基于小波规则的控制策略下峰值输出功率值大于基于规则的控制策略的,原因是锂动力电池在该策略中起功率缓冲器的作用,抑制燃料电池高峰值输出功率。在制动条件下,基于小波规则的控制策略考虑到高制动功率易损坏锂动力电池的使用寿命,因此只回收低制动功率条件下的低频部分,即Pbat=Pinf,其余制动力由机械制动摩擦生热消耗。 图10(c)所示为不同策略下锂动力电池SOC变化。从图中可以看出,基于小波规则的控制策略的SOC最小值为49%;基于规则的控制策略的为40%。结合图9,从总体变化来看,基于小波规则的控制策略下的锂动力电池SOC值大于基于规则的控制策略下的。 以百千米燃料电池的H2消耗量作为评价经济性的指标,通过与基于规则的控制策略下的百千米H2消耗量对比分析,2种工况下不同策略的百千米H2消耗量如表1所示。从表中可以看出,在典型城市道路行驶工况和中国典型城市工况下,基于小波规则的控制策略的百千米H2消耗量都比基于规则的能量管理策略的分别低6.64%和8.51%。 (a)燃料电池输出功率 表1 2种行驶工况下不同策略的百千米H2消耗量 本文中提出了一种基于小波规则的FCEV能量管理策略,将基于小波规则的控制策略与基于规则的控制策略进行比较,得出以下主要结论: 1)在不同行驶工况下,基于小波规则的控制策略均能很好地实现燃料电池复合能源之间的功率分配,保证了燃料电池工作在高效区间,燃料电池实际运行工作点效率值保持在50%~60%。 2)基于小波规则的控制策略能够抑制燃料电池高峰值功率的输出,最大不超过24.64 kW 3)2种行驶工况下,基于小波规则的控制策略的百千米H2消耗量比基于规则控制策略的分别低6.64%和8.51%。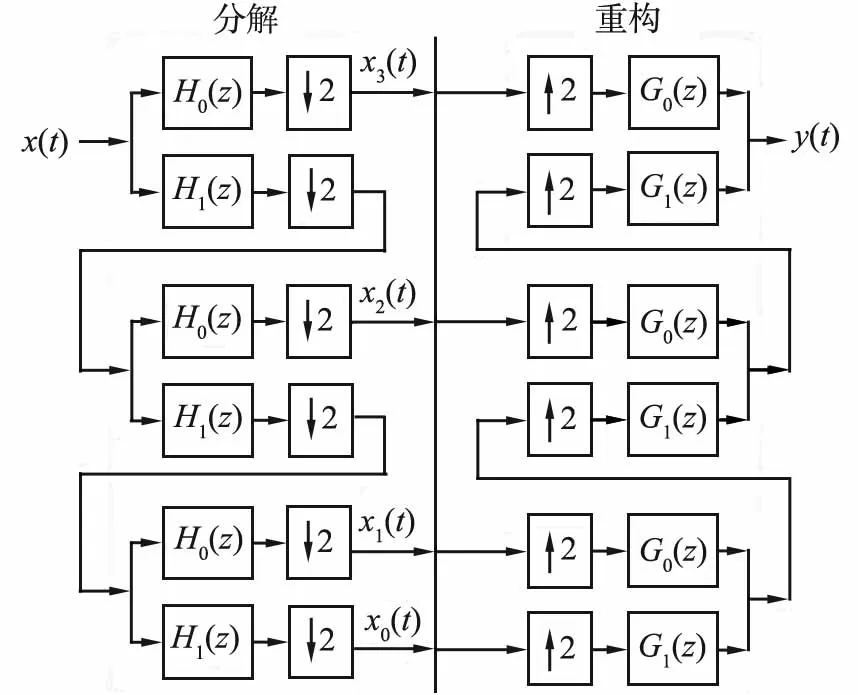
4 仿真结果与分析
5 结论

