电磁阻尼耦合悬架的内共振参数匹配分析

党 壮，刘灿昌，贺成泰，苏红建，张鑫越，栾军超

(山东理工大学 交通与车辆工程学院,山东 淄博 255049)

机电耦合系统因具有良好的电磁阻尼特性而广泛应用于振动能量回收和控制领域。耦合系统的几何和电磁非线性会影响结构振动的稳定性和控制效果，因此研究耦合系统的内共振特性具有重要的理论和应用价值[1]。机电耦合系统共振特性分析成为当前研究的重要课题之一。杨志安等[2-5]研究了电阻、电感、电容(RLC)串联电路系统与微梁系统固有频率之比为1∶2时的内共振特性以及耦合系统的吸合电压与电振荡，分析了RLC电路弹簧耦合系统的非线性振动和动力稳定性，得到该模型的稳定边界以及对于类似能量转化的规律。崔一辉等[6]建立RLC电路弹簧耦合系统模型，研究了RLC电路弹簧系统的非线性振动特性，得到级数形式解。马骏等[7]建立了三自由度车辆悬置系统1/4车辆模型，通过研究该系统垂向耦合的振动特性，得到了人体最敏感的频率范围。郑银环等[8]在七自由度车辆动力学模型的基础上，建立车辆振动模型，对耦合振动系统的特性进行分析，得到了路面情况对于耦合振动的影响规律。汽车悬架耦合系统存在建模和分析复杂的问题，研究工作者对悬架耦合非线性特性的研究较少[9-11]。汽车悬架耦合系统内共振耦合参数匹配关系是电磁阻尼悬架设计的关键问题之一，因此，开展电磁阻尼的悬架耦合系统共振特性研究对于电磁阻尼悬架设计具有重要的指导意义。

本文中以电磁阻尼悬架为研究对象，建立机电耦合动力学模型，研究电磁阻尼耦合悬架的内共振参数匹配关系。应用多尺度法分析耦合系统动力学微分方程，得到耦合系统的幅频响应方程。利用数值方法计算分析耦合系统的幅频方程，得到幅频方程的响应曲线,得到RLC电路电磁学参数与机械参数间的影响规律。

1 理论分析

电磁阻尼耦合悬架模型及其等效电路见图1。利用多项式拟合方法，得到模型的振动微分方程为

(1)

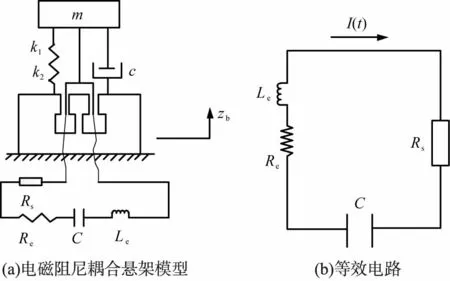
m—簧上质量；c—阻尼；k1—弹簧刚度；k2—非线性弹簧刚度；Le、Re—线圈的固有电感、电阻，Rs—分流器的等效电阻；C—电容；zb—外界激励幅值；I(t)—电流。图1 电磁阻尼耦合悬架模型及其等效电路

为了便于分析，引入无量纲量

(2)

式中：x为悬架无量纲位移；t为无量纲时间；ω为悬架固有角频率；Ω为无量纲外界激励频率；q为无量纲电荷量；Q0为最大电压时的电荷量。

(3)

应用多尺度法，求得方程(3)的近似解为

(4)

式中：T0=t为快变时间尺度；T1=εt为慢变时间尺度。

调节外激励的频率和悬架的固有频率成主共振关系，并且悬架的固有频率与电路系统的固有频率之比满足1∶3时，电磁阻尼耦合悬架会产生内共振，各频率满足关系为

(5)

式中σ1、σ2分别为悬架、电路的固有频率调谐参数。

将式(4)及其对时间的导数代入式(3)，并令式(3)中等号两侧ε的同次幂相等，整理得

(6)

式中O(ε0)为无量纲参数次数为0的项。

(7)

式中O(ε1)为无量纲参数次数为1的项。

式(7)的近似解为

(8)

A1、A2的极坐标形式为

(9)

式中：a1(T1)、a2(T1)分别为悬架、电路振幅的实部；β1(T1)、β2(T1)分别为悬架、电路的相位。

式(7)处理过程中使用变换

(10)

将式(8)、(10)代入式(7)，得到久期方程，即

2∂A1∂T1jω1+n1jω1A1+3n2A21A—1-12Ω2ejσ1T1+ 3n4jω1A—21A2e-jσ2T1=0,2∂A2∂T1jω2+u1jω2A2-13u3jω2A31ejσ2T1=0。ìîíïïïïïïï(11)

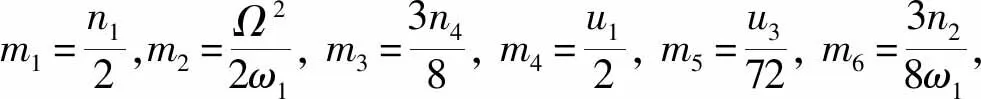
(12)

(14)

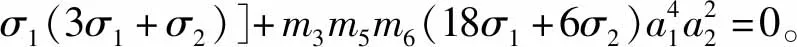
(15)

通过应用多尺度法，分析耦合系统动力学微分方程，得到系统的幅频响应方程。本文中根据式(14)、(15)对算例进行仿真分析，得到悬架系统和电路系统的相应特性。

2 算例分析

算例以电磁阻尼耦合悬架系统幅频响应方程为计算对象，通过改变电路中的电阻、电感、电压、外界激励幅值和频率等参数，研究电磁阻尼耦合悬架系统的内共振特性和参数匹配关系。算例参数[12-15]如表1所示。图2所示为不同参数对应的电磁阻尼耦合悬架系统幅频响应曲线，其中调谐参数σ2取为1。

表1 算例所需部分参数

图2(a)所示为Re-Rs>0条件下不同分流器等效电阻时的悬架幅频响应曲线。算例中电路采用的参数分别为Le=0.3 H，U=10V，Ω=0.06 rad/s和zb=0.04 m。由图可知，分流器电阻为1 600 Ω时的幅频曲线幅值最大，振动的非线性较显著。悬架幅频响应曲线的振动峰值随分流器电阻的增大而单调递增。

图2(b)所示为Re-Rs<0条件下不同分流器等效电阻时的悬架幅频。算例中的电路参数与图2(a)中的相同，并且满足分流器电阻小于线圈电阻的条件。由图可知，当分流器电阻为600 Ω时，幅频曲线幅值最大，振动的非线性较显著；当分流器电阻为1 000 Ω时，幅频曲线幅值最小，振动的非线性明显减弱，悬架幅频响应曲线的振动峰值随分流器电阻的增大而减小。

图2(c)所示为不同线圈固有电感时的悬架幅频响应曲线。算例中电路采用的参数分别为Rs=1 000 Ω，Ω=0.06 rad/s，zb=0.04 m和U=10V。由图可知，当线圈固有电感Le由0.3 H增大至0.5 H时，系统的最大振幅减小，并且系统振动非线性减弱。由此可得，当选取电感值在参数范围内，并保持其他参数不变时，电感值越大；悬架幅频响应曲线的峰值越小，振动非线性越弱。

图2(d)所示为不同电路电压时的悬架幅频响应曲线。算例中电路采用的参数分别为Rs=1 000 Ω，Ω=0.06 rad/s，zb=0.04 m和Le=0.3 H。由图可知，当电路电压U由10 V增大至20 V时，悬架振幅响应曲线峰值的变化规律和非线性强度的变化情况与改变电感数值时的相似，当选取电压值在参数范围内，并保持其他参数不变时，电压值越大，悬架幅频响应曲线的峰值越小，振动非线性越弱。

图2(e)所示为不同外界激励频率时的悬架幅频响应曲线。算例中电路采用的参数分别为U=10 V，Rs=1 000 Ω，zb=0.04 m和Le=0.3 H。当外界激励频率Ω从0.06 rad/s递减至0.04 rad/s时，悬架振动的非线性呈现一定的减弱，而悬架振幅响应曲线峰值逐渐增大。由此可得，当选取外界激励频率值在参数范围内，并保持其他参数不变时，数值越小，悬架幅频响应曲线的峰值越小，振动非线性越弱。

图2(f)所示为不同外界激励幅值时的悬架幅频响应曲线。算例中电路采用的参数分别为Ω=0.06 rad/s，Rs=1 000 Ω，U=10 V和Le=0.3 H。由图可知，外界激励幅值zb越小，对应的悬架幅频响应曲线的峰值越小。

图3所示为不同参数对电路幅频响应曲线的影响，其中调谐参数σ1取为0.01。

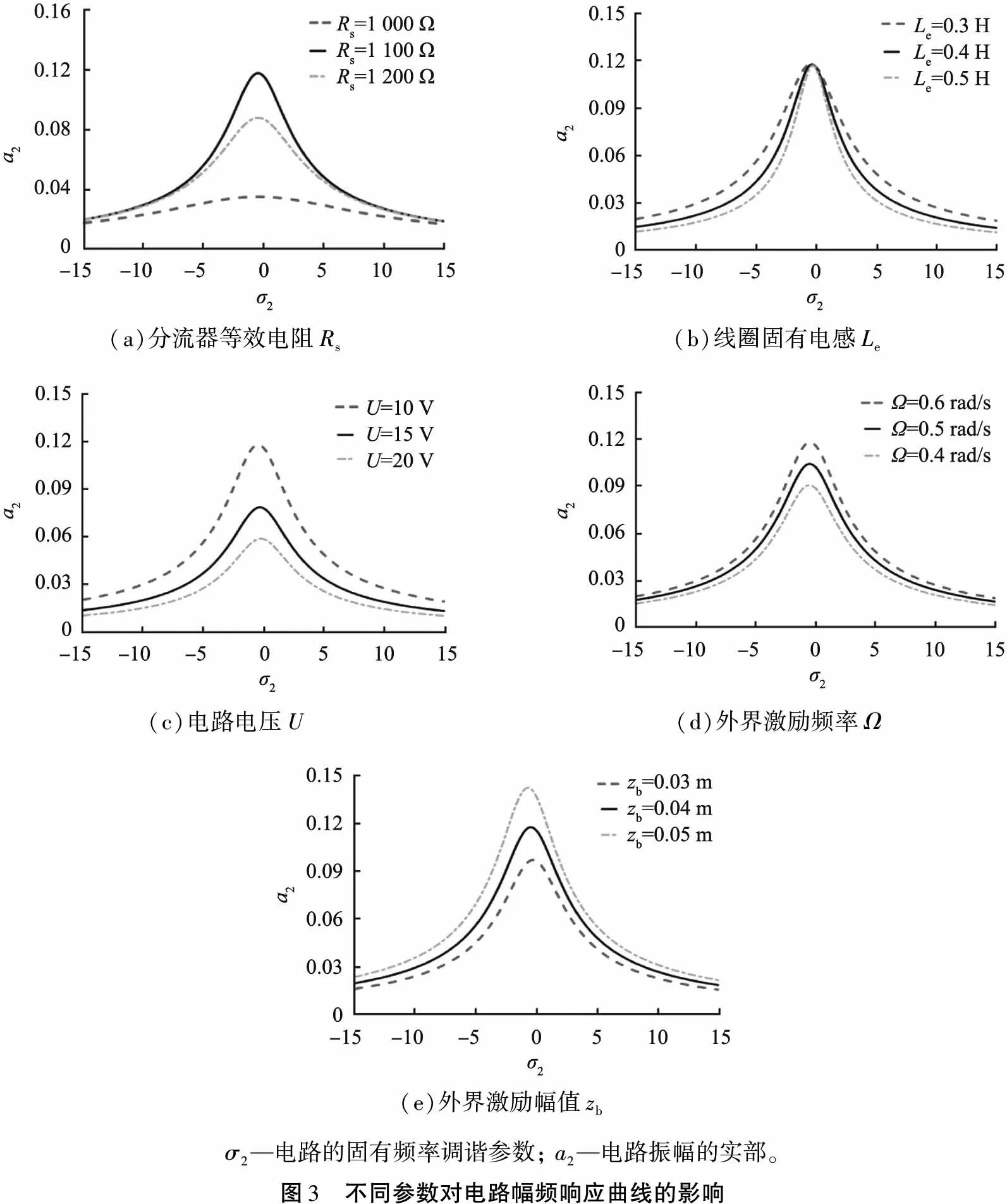
图3(a)所示为不同分流器等效电阻时的电路幅频响应响应。算例中电路采用的参数分别为zb=0.04 m，Ω=0.6 rad/s，Le=0.3 H和U=10 V。由图可知，当选取分流器等效电阻Rs在参数范围内,并保持其他参数不变时，电路的振幅响应曲线在接近满足完全调谐时达到峰值。随着分流器电阻Rs的增大，电路幅频响应曲线的峰值先增大后减小。

图3(b)所示为不同线圈固有电感时的电路幅频响应。算例中电路采用的参数分别为Ω=0.6 rad/s，zb=0.04 m，Rs=1 000 Ω和U=10 V。由图可知，随着线圈固有电感Le逐渐增大，电量振幅响应曲线的峰值几乎没有变化，但是电量振幅响应曲线的共振区变小。同时随着电感从0.3 H增大到0.5 H，响应曲线轻微右移，使得响应曲线更接近完全调谐。

图3(c)所示为不同电路电压时的电路幅频响应。算例中电路采用的参数分别为Ω=0.6 rad/s，zb=0.04 m，Rs=1 000 Ω和Le=0.3 H。由图可知，电量振幅响应曲线峰值随电路电压U的增大而逐渐减小，响应曲线共振区随电路电压的增大而变窄。

图3(d)所示为不同外界激励频率时的电路幅频响应。算例中电路采用的参数分别为Rs=1 000 Ω，Le=0.3 H，zb=0.04 m和U=10 V。由图可知，与电压对电量的振幅响应曲线影响相反，在外界激励频率Ω由0.4 rad/s增大至0.6 rad/s的过程中，电量的振幅响应曲线峰值单调递增。

图3(e)所示为不同外界激励幅值时的电路幅频响应。算例中电路采用的参数分别为Rs=1 000 Ω，Ω=0.6 rad/s，Le=0.3 H和U=10 V。由图可知，当外界激励幅值zb为0.03 m时，电量的振幅响应曲线在接近于满足完全调谐时达到峰值。增大外界激励幅值能使响应曲线振幅增大，同时，峰值向完全调谐的左侧略有偏移。

3 结论

本文中建立了受简谐激励的电磁阻尼耦合悬架动力学模型及非线性振动微分方程，分析得到耦合系统中悬架与电路系统固有频率之比为1∶3时的内共振幅频方程，通过算例分析耦合系统的幅频响应曲线，得到了电磁阻尼耦合悬架系统的内共振特性和参数匹配关系。

1)调节分流器电阻值接近线圈固有电阻值，悬架幅频响应曲线的峰值随着电感、电压的增大而减小，外界激励幅值和频率的减小，会使悬架对应的幅频响应曲线的峰值减小，悬架幅频响应曲线的非线性强度随着电感和外界激励幅值的增大而减小。

2)电量振幅响应曲线的峰值在调节分流器电阻值接近线圈固有电阻时达到最大，电量的振幅响应曲线峰值随外界激励幅值和频率的增大而增大，而电感对电量的振幅响应曲线的峰值影响微小，只是随着电感的增大，响应曲线的共振区逐渐变窄。