测试围压条件下水泥固化海泥应力 - 应变模型

边晓亚, 程宇熙

(武汉工程大学 土木工程与建筑学院， 湖北 武汉 430074)

随着沿海城市的快速发展，许多沿海城市开展大规模的河湖淤泥疏浚工作，且力度逐年加大[1]，淤泥的处理也成为沿海城市重大难题之一，给沿海地区带来了巨大的环境问题和经济压力[2]。为解决上述问题，日本工程界发展了一种新的围海垦地工作模式，即将原状海泥、水与低剂量固化剂(水泥等)混合形成水泥固化流塑态填料并通过泵送管道直接浇注到垦地区域，待海泥 - 水 - 固化剂混合物硬化之后，便形成了满足一定工程力学指标的建筑场地SDF(Standard Delay Format)技术。

水泥固化黏土技术早已受到岩土界的关注，大量学者对其强度影响因素及其特性进行了研究，如吴燕开等[3]得出了固化土在不同离子浓度的海水和蒸馏水养护条件下无侧限抗压强度变化规律；Pongsivasathi等[4]研究了水泥掺量对水泥土强度的影响；Yin等[5]发现，对于饱和水泥固化黏土，含水率对强度有显著影响。本文以SDF技术中的“低掺量水泥固化高含水率黏土(HW-CSC,High Water Content-Cement Stabilized Clay)”为对象开展研究，一些学者已对HW-CSC的强度特性开展了研究，如张春雷等[6～8]研究了不同水灰比以及养护压力对HW-CSC试样强度的影响；章荣军等[9]研究了养护温度对HW-CSC强度的影响；李建军等[10～13]提出了不同养护时间、不同含水量与水泥掺量配合比下HW-CSC的强度发展情况。上述系列研究成果可认为是当前水泥固化土强度因素影响研究的代表性成果，但其对水泥固化黏土的变形特性研究较少。

另外，也有学者针对传统水泥固化土本构模型，包括水泥固化黏土应力 - 应变关系开展了研究，Santoso等[14]利用多变量正态模型对SDF的强度特性进行概率估计，证明了模型的可行性。朱剑锋等[15]提出了一个能涵盖固化剂掺量影响并能实现应力 - 应变关系转型的镁质水泥固化土本构模型。Mollamahmutoglu等[16]研究了湿养护和风干条件下超细水泥稳定黏性土不同时间间隔的抗剪强度参数和应力 - 应变特性。

由于HW-CSC具有水泥剂量少、搅拌不均等特征，传统的本构模型不适用于HW-CSC材料，而且测试围压的影响，也是应用HW-CSC所必须考虑的因素。针对上述情况，本文拟利用海泥开展室内试验研究，通过分析试验结果，提出适合不同测试围压条件下HW-CSC材料的应力 - 应变关系统一模型，并分析测试围压对于HW-CSC材料应力 - 应变关系模型的影响，开展这些工作将有助于弄清测试围压对HW-CSC材料强度和变形的影响规律。

1 试验材料及步骤

1.1 试验材料

本试验主要材料有海泥、水、水泥，其中海泥取自温州地区浅海区域上层的海泥，其力学特性指标为：比重为2.69、液限为53.7%、塑限为26.5%、有机质含量为4.41%、砂粒含量(0.075～2 mm)为14.9%、粉粒含量(0.002～0.075 mm)为79.5%、黏粒含量(<0.002 mm)为5.6%、USCS(Unified Soil Classification System)土壤分类为可塑性黏土。

试验所用水泥是工程上常用的早强复合硅酸盐水泥，即PC 32.5R水泥。

1.2 试验步骤

(1)将内径36 mm的塑料管分割成80 mm一段，内壁抹上凡士林，一端用透明胶带封住，作为HW-CSC的模具。

(2)按照图1所示的配合比分布范围及海泥的天然含水量计算出所需水泥和水的质量。

(3)将计算确定的水和水泥按次序加入海泥中，并将水泥土搅拌均匀。

(4)分3～4层用抹刀将HW-CSC装入塑料管中，每层经充分震动排出管内空气后，再装下一层，重复直至装满，装满后将上表面用抹刀刮平。

(5)将装好的模具放入自封袋中，排出袋内空气封口，将自封袋放入装满水的桶中浸没，放置于实验室[温度20±3 ℃，湿度>80%]养护，待其达到设计龄期，进行脱模。

(6)将脱模后的试样两端用切土刀修整，使试样两端面垂直于轴线，高度为直径的两倍。

(7)将脱模后的试样放入三轴仪中，设置相应测试围压(拟设置4种情况围压：20，40，60，80 kPa)，开始测试其抗压强度。

(8)操作过程严格按照规范JIS A1216：2009执行[17]。

图1 试样配合比分布范围

2 试验结果分析

2.1 HW-CSC试样的应力 - 应变关系基本规律

从试验数据中选取有代表性的95组HW-CSC应力 - 应变的数据，其应力 - 应变关系如图2所示。

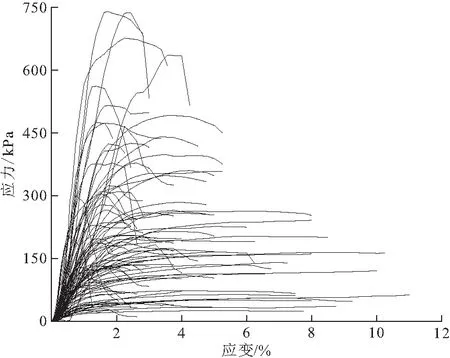
图2 95组HW-CSC应力 - 应变关系

由图2分析可得，HW-CSC极限强度对应的极限应变有一些在2%左右(大致分布于1%～3%之间)，也有很多大于3%，这与没有施加测试围压的HW-CSC试样有所不同。当HW-CSC强度较大时，其在达到屈服强度前的增长速率非常快，极限应变也非常小。在达到屈服强度之后，强度迅速下降，从测试完毕试样的破坏形式来看，大部分表现为脆性破坏。

当HW-CSC的强度较小时，其应力随应变增大的速率很慢，极限应变也变得很大。在达到极限强度之后，应力-应变曲线在极限强度附近处于类波动状态，根据其破坏试样的形式来看，低强度的HW-CSC表现为一种延性破坏。

从上述试样应力 - 应变关系曲线的特性来分析，施加不同测试围压所得到的应力 - 应变曲线趋势基本相同，可以定性推断，能够找到一个统一形式的函数来描述HW-CSC屈服之前的应力 - 应变关系。

2.2 不同测试围压下HW-CSC试样的应力-应变模型比较

2.2.1 拟合分析

筛选出拟合程度较理想的模型，有利于后期比选出一个适合所有测试围压条件下的应力 - 应变函数模型。

将4种测试围压的HW-CSC应力 - 应变曲线进行模型拟合分析，最终筛选出了4种拟合度较高的模型，如表1所示。

表1 四种拟合模型

2.2.2 拟合效果比较

对选出的4种模型进行模型比对，筛选出最合适的函数模型。模型对比时，只需要比较两个模型AIC值的大小，AIC值越小表示模型拟合越好，正确的可能性也就越高。例如，如果模型2的拟合效果比模型3的拟合效果好，将结果记为2>3。重复上述步骤，得出4种测试围压下，4种模型对于HW-CSC应力 - 应变曲线模拟的比较结果如表2所示。

表2 四种模型对95组HW-CSC应力 - 应变试验数据的拟合比较结果

从表2分析得出，4种模型的拟合程度准确性从大到小为：Extreme>Gaussian>Giddings>Gauss。经过上述分析可以得出，Extreme模型的准确性在4种模型里面是最高的，而且Extreme模型形式比较简单，是合适的拟合函数。

上述结果表明，Extreme模型精度高且形式较为简单，宜选用Extreme模型来拟合HW-CSC的应力 - 应变关系。因此，可以将HW-CSC的应力 - 应变函数关系模型表述为：

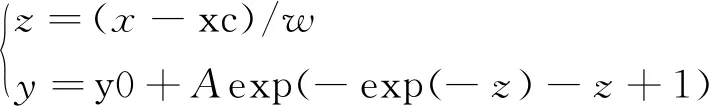
(1)

2.3 HW-CSC应力 - 应变拟合模型中各参数分布特征

为研究模型Extreme中4个参数对HW-CSC应力和应变的影响，将模型Extreme下，95组数据的参数y0，xc，w，A提取出来，并将95组数据的极限强度和极限应变一一列出。根据列出的数据，给出4个模型参数的分布特征图(图3)。进一步将95组数据按极限强度大小排序画出参数y0，xc，w，A的分布图(图3a)。再按照极限应变大小排序，给出4个参数的分布图(图3b)。

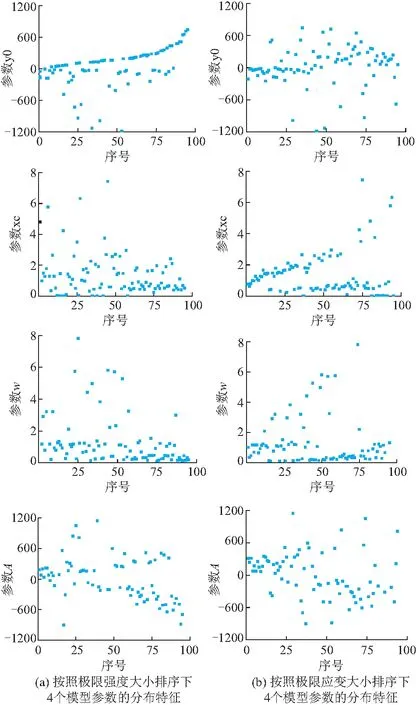
图3 模型参数散点分布特征

将95组试样分别按极限强度和极限应变大小排序，图3a和图3b分别给出了4个模型参数的散点分布情况(横坐标序号与相应极限强度和极限应变大小顺序一致)。由图3a和图3b可以得知：参数y0随着HW-CSC应力的增大而增大，随着应变的增大也基本呈现增长趋势，但增长速度缓慢；参数xc和w在随应力增长图像中没有明显规律，趋于平缓；而在随着应变增长的时候，基本呈现出增长的趋势；参数A大致随着应力与应变的增加而减小。

由上述分析可知，4个参数对于HW-CSC应力 - 应变的影响为：

(1)分析式(1)和图3可知，参数xc和w主要控制着函数达到峰值时所对应的横坐标，即为HW-CSC试样的极限应变值。

(2)参数y0和A主要控制着函数的纵坐标，即为试样所对应的极限应力的值。

(3)参数y0，xc，w，A基本都对函数的极限应变有影响，其中影响最大的是参数xc和w，极限应变随着这两个参数的增大而快速增加。参数y0对于极限应变的影响很小，但基本呈现斜率较小的正比例关系。参数A与极限应力呈现负斜率的正比例关系。所以极限应力随y0的增加而增加，随A的减小而增加。

2.4 测试围压对模型参数的影响

图4～图7分别给出了20 kPa(共23组数据)、40 kPa(共24组数据)、60 kPa(共24组数据)、80 kPa(共24组数据)等4种测试围压下参数y0，xc，w，A的分布情况。

图4 四种测试围压下参数y0的分布

图5 四种测试围压下参数xc的分布

图6 四种测试围压下参数w的分布

图7 四种测试围压下参数A的分布

由图4～7可知：参数y0随着测试围压的增大而增加；参数xc随着测试围压的增加先增加后减小，40 kPa测试围压时，xc值最大，40 kPa之后逐渐减小；参数w与xc趋势相同；A随着测试围压的增加呈现下降趋势。

2.5 测试围压对HW-CSC试样应力 - 应变模型的影响

通过分析应力 - 应变模型参数y0，xc，w，A的分布特征以及围压对参数y0，xc，w，A的影响，可以得出围压对应力 - 应变模型的影响，即：

(1)参数y0和参数A主要是控制HW-CSC的极限应力，参数xc和参数w主要控制HW-CSC的极限应变。

(2)测试围压通过影响参数y0和A从而间接影响模型中HW-CSC的极限应力，测试围压越高，极限应力越大。

(3)测试围压通过影响参数xc和w来间接影响模型中HW-CSC的极限应变，测试围压在小于40 kPa的时候，对试样的极限应变有促进作用；测试围压在大于40 kPa时，对试样的极限应变有抑制作用。xc和w两个参数与含水率对HW-CSC的强度影响基本相同。而40 kPa测试围压的时候，参数xc和w达到最大值。因此随着测试围压的增加，极限应变先增加后减小。

(4)测试围压的增大可以使得参数y0增大，A减小，从而提高HW-CSC的极限应力。因此y0与水泥掺量和龄期对HW-CSC极限应力变化的影响是一致的；而A与含水率一样都对HW-CSC极限应力变化起消极作用。同时测试围压的增大使得xc和w先增大后减小，但从总的分析结果来看，测试围压的增大导致HW-CSC强度增加。

(5)实验结果分析表明，施加测试围压对HW-CSC试样强度有促进作用，而测试围压在小于40 kPa时，对试样的强度促进效果较低，而测试围压大于40 kPa时，测试围压对HW-CSC试样强度促进效果较高。因此，施加测试围压大于40 kPa对HW-CSC试样的强度促进效果更好。

3 结 论

(1)基于室内三轴试验结果，对HW-CSC试样的应力 - 应变关系进行研究，通过定性与定量分析，最终确定了精度较高、形式较为简单的Extreme函数模型来拟合HW-CSC的应力 - 应变关系。

(2)Extreme函数存在4个参数y0，xc，w，A，通过进一步研究得出每个参数具体对应力 - 应变模型的影响，经过分析，参数y0增大，A减小会使HW-CSC的极限应力增大；参数xc和w增大，HW-CSC的极限应变会增大。

(3)随着测试围压的增加，极限应力不断增大。而随着测试围压的增大，极限应变是先增大后减小，其峰值出现在围压为40 kPa的时候。因此，建议在实验中对HW-CSC试样施加的测试围压大于40 kPa。