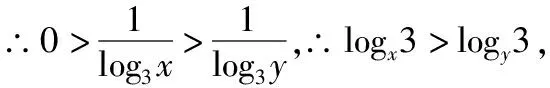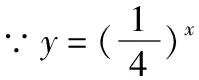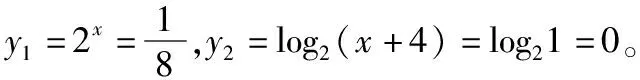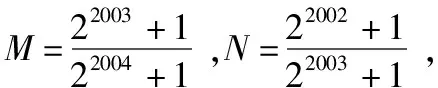浅谈高中数学选择题的解题方法

张福庆

(福建省德化第一中学 福建 德化 362500)

1.直接法

直接法就是直接由题目的条件出发，利用与题目条件相关的知识内容求出结果的方法。

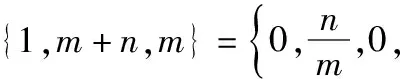
A、-2 B、2 C、-1 D、1

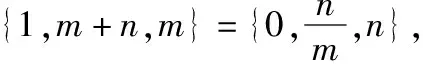
从而m=-1，n=1，n-m=2。故选B.

2.筛选法

筛选法，也称排除法.当直接从题目条件出发推出正确答案比较困难时，可以考虑从答案出发，排除掉一些错误的选项，从而得到正确答案。

例2:若0

A、3y<3xB、logx3

解析：∵y=3x在R上是增函数，且0

∵y=log3x在(0,+∞)上是增函数，且0

3.特殊化法

考虑到选择题答案的唯一性，可以将题意特殊化，从而降低题目难度，选出正确选项。

例3:设直线l与抛物线y2=2px(p>0)相交于M、N两点，O为坐标原点，若OM⊥ON，则直线l与x轴的交点为( )

解析：考虑到直线l与x轴的交点，仅由OM⊥ON确定，而与l的倾斜角无关，因此，可以采用特殊值法求解，不妨取l⊥x轴来探求问题的解。取l垂直于x轴，OM的方程为y=x，联立y2=2px，得M(2p,2p)，故l与x轴的交点为(2p,0)，选C。

4.验证法

从选择题的选项出发，把选项代入题目逐一验证，得到正确的答案。

解析：将四个选项逐一代入验证，易知A、B、C三个选项都不符合题意，而D选项符合题意，故选D。

5.特征分析法

从题目提供的条件出发，认真分析题意，努力找出其中的特征，如结构特征、数字特征等，发现规律，排除错误选项，快速锁定正确答案。

6.估算法

立足选择题的题型特点，在一些特殊的数学问题中，通过合理的估算就可以排除一些干扰选项，进而找到正确答案，但它对学生数学思维的层次要求较高。

例6:已知P，Q，R为球面上的三点，过它们的截面和球心的距离等于球半径的一半，且PQ=PR=RQ=2，则球面面积等于( )

7.特殊结论联想法

就是利用在学习数学知识过程中，归纳出来的一些数学性质、结论，结合题目中涉及的问题展开大胆联想，从而使问题得到解决的方法。

A、4-mB、4 C、2mD、2m-4

解析：应用重要结论△MF2N的周长等于4a+2|MN|可知，△MF2N的周长等于4cosα+2m，因此最小值等于2m。故选C。

8.数形结合法

当方程比较复杂的时候，方程的根的个数问题往往要转化成函数图象的交点个数问题.通过作出方程左右两边的函数对应的图象，就可以直观地看出交点的情况，进而解决方程的根的问题。

例8：方程2x=log2(x+4)的根的情况是( )

A、有两个负根 B、仅有一根

C、有一正根一负根 D、没有实数根

解析：令y1=2x,y2=log2(x+4)。画草图(略)。

当x=0时，y1=2x=1,y2=log2(x+4)=2。∴y1

当x=2时，y1=2x=4,y2=log2(x+4)=log26。∴y1>y2。

∴y1>y2。

由此可知，两条曲线的在区间(-3,0)和(0,2)内均有一个交点，故选C。

9.类比法

类比法就是将未知的对象和已知的对象进行对比，以已知对象的性质推知未知对象的性质的方法。

A、MND、无法确定

10.构造方程法

构造方程法是根据题目问题的特点，通过构造方程或者方程组来求解问题的方法。

例10：已知f(x)是偶函数，g(x)是奇函数，且f(x)+g(x)=3x2-3x+2,则f(-1)=( )

A、-5 B、5 C、-4 D、4

解析：本题主要是利用函数奇偶性构造方程组求解。令x=1,得f(1)+g(1)=2，令x=-1得f(-1)+g(-1)=8。两式相加得：f(1)+g(1)+f(-1)+g(-1)=10，即2f(-1)=10，f(-1)=5。故选B。

直接法、筛选法、特殊化法、验证法、推理分析法、估算法、特殊结论联想法、数形结合法、类比法、构造方程法，这十种解法是高中数学选择题的常见解法.本文主要就是结合具体的例题将这十种解法作一个简单的介绍。当然，高中数学选择题的解法还有很多，例如极限法、构造函数法等，这里只是对选择题的常见解法作一个部分的归纳，希望通过这些常见解法的介绍，可以让学生今后在做选择题时，能结合题目的条件，恰当地选择相应的解题方法，真正提高选择题的解题效率。