三角形的内角和 教学设计

一、课前分析

三角形的内角和是青岛版数学四年级下册的教学内容。其实通过课前调研我们发现有很多学生在上课前已经知道“三角形的内角和是180°”的结论，但不清楚其中的道理。所以在这种情形下，本节课的教学重点不在于了解，而在于验证。常规的教学大多让学生将三个角剪下来进行拼接实验，或者用量角器去量，但操作过程中难免会有误差，也许就得不到180°，甚至还会出现利用结论拼凑结果的现象。其实，数学上很多概念并不是完全靠实验得到的，“不讲证明，数学课就失去了灵魂”。本节课上，我们把“动手操作”和“演繹推理”结合起来，让学生了解数学的本质，触摸数学的灵魂。

二、教学目标

1、经历探索三角形内角和的研究过程，感受数学的研究方法，培养大胆质疑的态度和严谨科学的精神。

2、学习主动探究新知的方法，了解转化迁移的数学思想。

3、发展合情推理能力和演绎推理能力。

三、教学重难点

通过实践操作和演绎推理，推导出三角形内角和等于180°。

四、教学过程

（一）从学生的认知起点出发，提出质疑

1、认识三角形的内角和内角和定义。让学生通过画出内角，明确内角定义。

（二）通过实践操作，发现三角形内角和大约是180°

1、合作探究

引导学生思考，可以通过什么方法知道三角形的内角和（量、剪、拼）。三角形按角分类可以分成：直角三角形、锐角三角形、钝角三角形，我们每一类研究一个。

小组探究要求

1、小组议——组内6人商量，选择一种方法研究三角形的内角和;

2、个人做——每人拿一个三角形，用此方法得到它的内角和，记录下来;

3、齐交流——组内汇总各自探究结果，填写探究单，记录“我们的发现”。

2、汇报发现

在学生汇报的过程中，我们要格外关注那些测量结果接近180°学生的测量过程，引导学生思考通过“量”和“拼”的方法能准确确定三角形的内角和吗？

（三）通过计算推理，得出三角形的内角和一定是180°

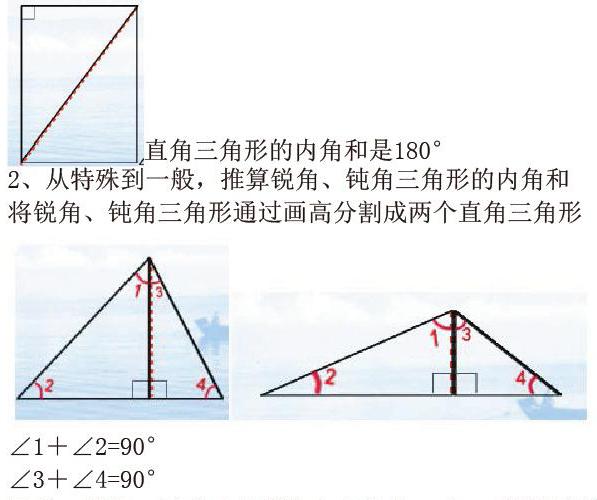
1、从特殊入手，推算直角三角形的内角和

思考：能不能把直角三角形转化为已知内角和的图形呢（我们用两个完全相同的直角三角形可以转化为长方形）。长方形的内角和是360°，

2、从特殊到一般，推算锐角、钝角三角形的内角和

将锐角、钝角三角形通过画高分割成两个直角三角形

因此，锐角、钝角三角形的内角和是180°，所以任意三角形的内角和都是180°。

（四）全课总结

谈收获：引导学生发现数学真理美。

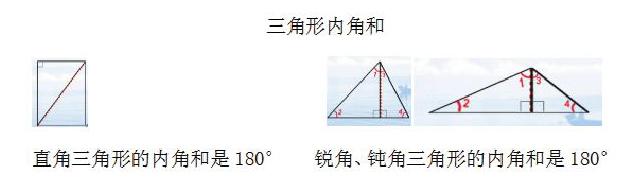
五、板书设计

所以任意三角形的内角和都是180°。

六、教学反思

在本次的授课过程中，我们通过量、剪、拼等实践活动，使学生初步感知三角形的内角和，在此基础上，提出“通过测量几个三角形就可以证明所有的三角形的内角和是180度”和“我们把没测量出三角形内角和是180°的原因归结为误差是否合理”这两个问题，进而把数学课提升到“验证”的高度，使学生通过转化和知识迁移验证出结论。本节课虽没有练习，却通过“动手操作”和“演绎推理”让学生了解数学的本质，触摸数学的灵魂。

山东省德州市天衢东路小学  陈红娣