基于影响矩阵的矮塔斜拉桥索力二次优化方法的研究

王占飞，黄 昊，全 伟，杨非凡

(1.沈阳建筑大学交通工程学院，辽宁 沈阳 110168；2.黄山学院建筑工程学院，安徽 黄山 245041)

矮塔斜拉桥是介于普通斜拉桥和梁式桥之间的一种新型组合结构体系，具有“塔矮、梁刚、索集中”的特点[1]。矮塔斜拉桥的整体刚度是由主梁与斜拉索共同提供的，根据刚度分配原则，通常主梁提供70%刚度，斜拉索提供30%刚度，所以对矮塔斜拉桥的索力进行优化可以改善结构的受力性能[2-5]。斜拉索的索力作用既体现主梁挠度，塔顶横向位移，主梁、主塔的内力对桥体的影响，又通过对主梁的加劲作用，改善主梁的受力性能，保证结构的安全性[6]，因此需要对矮塔斜拉桥索力优化问题进行研究。

对于斜拉桥的索力优化，国内外学者给出很多方法。A.M.B.Martins等[7]根据主梁位移与极限位移的比值以及拉索应力与容许应力的比值作为目标函数求得优化索力。Chen等[8]在刚性支承连续梁法基础上用迭代求解的方法求得优化索力。郭钟群等[9]提出了在主梁应力可行域范围求得优化索力。康春霞等[10]提出斜拉桥三种合理施工阶段拉索计算方法并进行了对比分析。苑仁安等[11]根据斜拉索索力调整的无应力状态法求得优化的索力。现有的索力优化研究主要针对常规斜拉桥，但与常规斜拉桥相比，矮塔斜拉桥梁体较刚以及索塔较矮，因此需要新的设计方法。基于此，笔者根据矮塔斜拉桥的结构特点，以某客专特大桥为例，提出二次优化的方法，根据影响矩阵的思想，采用多约束的影响矩阵法和直线内插法相互配合，不仅可以最大程度考虑实际受力的影响，还可以保证桥梁结构内力和线形的均匀，为同类型桥梁研究提供了理论基础。

1 计算模型

1.1 工程概况

某客专特大桥为新建邯济铁路至胶济铁路联络线工程上的一座独塔双索面预应力混凝土矮塔斜拉桥，该桥全长240 m，桥跨布置为(120+120)m，主桥位于曲线上，曲率半径为800 m，线间距为4.4 m。桥梁中支点截面梁高7.0 m，跨中及边跨等高段截面梁高5.0 m，桥面宽度为14.8 m，索塔附近桥宽加宽到16.5 m。梁顶板厚除支点附近外均为0.4 m，腹板厚按折线变化分别为0.5 m、0.7 m、0.8 m，底板厚按折线变化分别为0.4 m、0.7 m、1 m。斜拉索横向为双索面，立面为半扇形布置。索塔塔高在桥面以上为29.7 m，索塔为钢筋混凝土结构，每个索塔设10对斜拉索，塔上索距1.1 m，梁上索距8.0 m。该桥墩墩身采用实体墩，桥墩底部纵向宽度6.0 m，横向宽度16.5 m，承台高度5.5 m，采用桩径为2.0 m的钻孔灌注桩基础。矮塔斜拉桥整体构造如图1所示。

1.2 模型建立

采用有限元软件建立矮塔斜拉桥模型，桥梁主梁、桥墩和主塔均采用梁单元模拟，斜拉索采用桁架单元模拟，塔、梁、墩固结处采用刚性连接，拉索与主梁及桥塔的连接采用刚性连接。全桥共划分210个节点和176个单元，其中梁单元136个，桁架单元(斜拉索)40个。斜拉索左侧最外侧拉索为T10，最内侧拉索为T1；右侧最外侧斜拉索编号为P10，最内侧拉索为P1。有限元模型如图2所示。

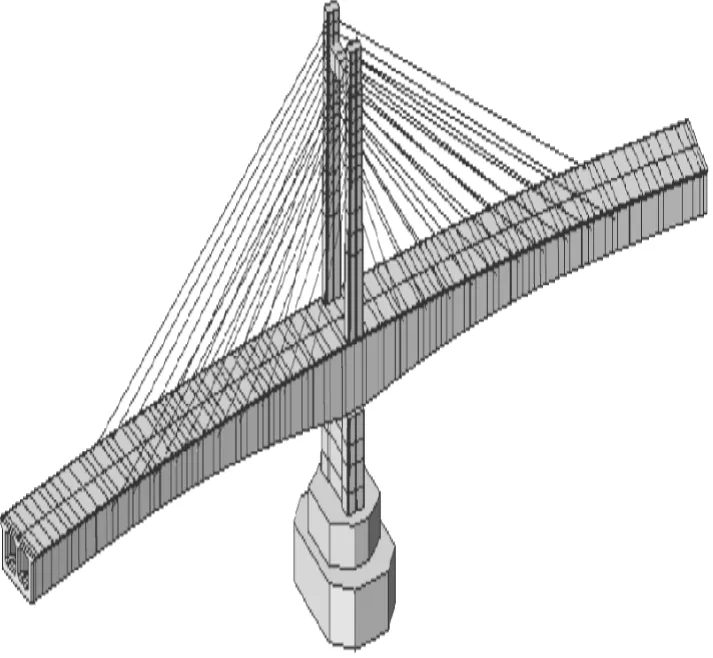
图2 矮塔斜拉桥有限元模型Fig.2 Finite element model of the extradosed cable-stayed bridge

2 索力优化计算原理

2.1 影响矩阵法

和常规斜拉桥相比，矮塔斜拉桥因为跨径较小且有较长一段的无索区，所以拉索较短，产生的垂度效应较小，因此可以采用基于线性叠加原理的影响矩阵法和直线内插法两种方法相互配合进行索力优化。当采用影响矩阵法进行优化索力时，既可以同时考虑某些节点位移、截面内力或索力对整体结构产生的影响，又可以通过目标函数最小化从而使得整个结构的位移、弯矩及索力达到最优解。而直线内插法则可以保证施工阶段桥梁结构内力和线形的均匀，两种方法相互配合可以使优化结果更加合理。

计算时可以将矮塔斜拉桥的塔梁单元假定为等截面杆系单元，桥梁整体结构弹性模量、惯性矩沿单元长度保持不变，则结构的应变能可表示为[12]

(1)

式中：m为全桥结构单元总数；M为第i号单元左右两端的弯矩；N为第i号单元左右两端的轴力；Ei、Ii、Ai、Li分别为第i号单元材料弹性模量、截面惯性矩、截面积、单元长度。

在考虑不计桥梁自重和斜拉索初张拉力为零的情况下，通过索力的施加使拉索单元发生变化，采用有限元程序，基于矮塔斜拉桥整体结构模型,可以计算得到当斜拉索单位索力发生变化时对全桥结构整体状态的影响向量,全桥整体结构与索力关系的表达式如下：

Z=Ax+Z0.

(2)

式中：x为斜拉索初张拉力组成的列阵；Z0为桥梁结构在自重下各单元的内力或位移的列阵；Z为桥梁结构在索力和自重下各单元的内力或位移的列阵；A为在单位索力作用下位移和弯矩的影响矩阵。

把式(2)带入到式(1)中：

U=xTGx+2Fx+P.

(3)

在式(3)的基础上提出优化过程中需要的约束条件，则式(3)为[13]

minU(T)=TTGT+2FT.

(4)

约束条件如下:

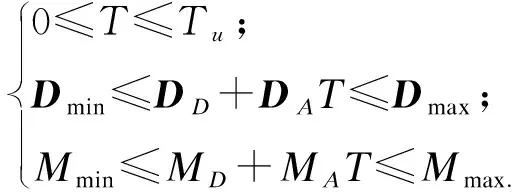
式中：T为索力值；Tu为索力的上限；Dmax和Dmin为约束塔梁位移上下限的极限值；Mmax和Mmin为约束塔梁内力或应力上下限的极限值；DD为在桥梁自重下的节点位移列阵；DA为结构位移响应的单位索力影响矩阵；MD为在桥梁自重下的内力或应力的位移列阵；MA为结构内力或应力响应的单位索力影响矩阵。

通过式(4)把矮塔斜拉桥的初张拉力优化过程转化为有约束的二次规划问题，求解该方程可以得到合理成桥索力。

2.2 直线内插法

通过影响矩阵法计算得出矮塔斜拉桥的优化索力，不仅能够保证桥梁整体结构，还能初步形成矮塔斜拉桥的结构受力体系。但是本次主梁施工采用满堂支架法，由于满堂支架法施工时主梁浇筑梁段较长并且刚度过大，单次优化可能无法达到理想成桥状态，为了保证优化结果的准确，需要根据矮塔斜拉桥的索力与结构整体线形和内力要求，再进行二次优化。由于对斜拉索进行第二次优化时桥梁整体结构受力体系已经完成，桥梁结构边界条件不会发生改变，可以直接把合理成桥索力值作为优化目标，采用直线内插法进行正装迭代计算[14-16]。

直线内插法的原理[17]是将理想成桥索力表示为T，成桥状态的控制参数值为Fm×1,在计算过程中，设斜拉索单位力张拉时控制参数的增量为a，与矮塔斜拉桥合理成桥状态的差值b为

b=F0-F.

(5)

对斜拉索索力调整量为x，则可得：

ax=b.

(6)

根据调整量采用直线内插法计算得到新的张拉索力:

T2=T1+xT2.

(7)

直线内插法的迭代收敛原则如下：

(8)

式中：s1在[0.005,0.02]内；s2在[0.01,0.05]内，根据精度确定范围。若计算结果满足收敛准则，则迭代停止;否则，按照相同方法进行下一轮迭代计算，进而得出二次优化的索力值。

3 结果分析

3.1 索力优化结果

笔者基于上述计算方法，对某客专特大桥进行索力优化分析，在考虑桥梁自重，二期铺装层重量以及预应力荷载，同时考虑混凝土收缩、徐变影响的基础上，求解矮塔斜拉桥的影响矩阵。优化约束条件如下：初张力的上限为8 000 kN，斜拉索与主梁相交节点垂直方向的位移限制条件为-0.15～0.1 m，同时塔顶顺桥向位移限制为-0.01～0.01 m，主梁的塔根弯矩值限定在-120 000 ～120 000 kN·m，其他位置弯矩值限定在-80 000～80 000 kN·m。对于上述计算，可以利用Matlab工具箱进行求解，在迭代12次后可以得到第一次优化的索力。

根据前文中索力二次优化的计算方法,把第一次优化后的索力值作为初始张拉索力进行差值迭代计算。在优化过程中，充分考虑施工阶段混凝土的收缩和徐变以及结构的非线性，对于矮塔斜拉桥拉索二次优化索力数值经过多次迭代计算后确定，得出优化索力满足精度要求，从而计算出二次优化索力。

将优化索力与工程实际设计索力进行对比，结果如图3所示。从图中可以看出，优化后索力分布均匀，同时索力满足两边大，中间小的特征；优化后拉索总索力与设计总索力相差不大，可以实现总用索量不变而改善桥梁受力。

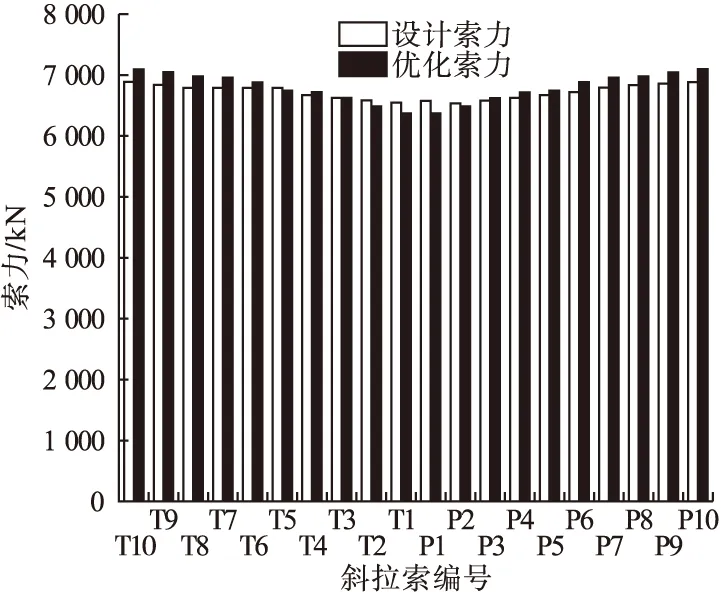
图3 优化前后索力对比图Fig.3 Comparison between the cable force before optimization and after optimization

在索力优化中，荷载组合中的结构自重、二期恒载、预应力、隔板自重都属于恒载。主力+附加力荷载组合由恒载、活载、温度荷载、横向风荷载组成。将恒载作用下的索力与主力+附加力荷载组合作用下的索力进行对比，结果如图4所示。

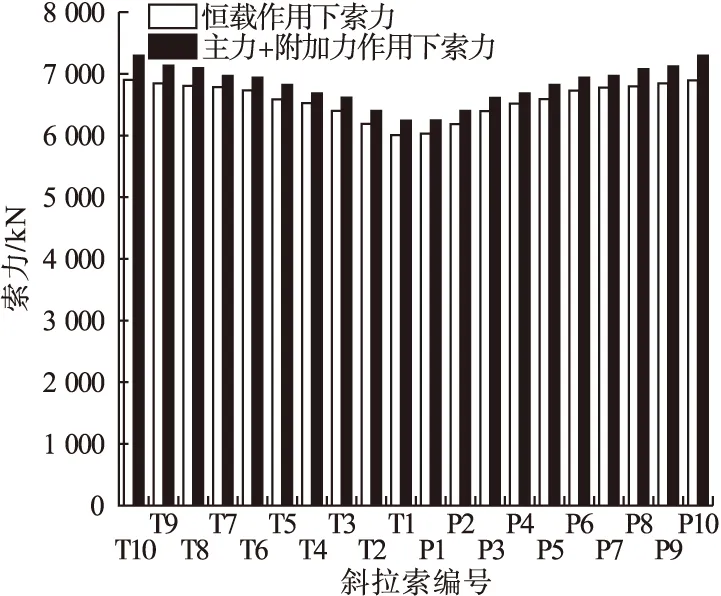
图4 恒载作用和主+附作用的索力对比图Fig.4 Comparison between the cable force under the constant load and main,additional load

从图中可以看出，恒载作用下的索力与主力+附加力荷载组合作用下的索力差距较小，其中差值最小的为P1号拉索，差值为181 kN；差值最大为P10号拉索，差值为359 kN。

3.2 主梁弯矩结果对比

优化前后在恒载作用下的主梁弯矩图如图5所示，优化前后主力+附加力荷载组合作用下的主梁弯矩图如图6所示。

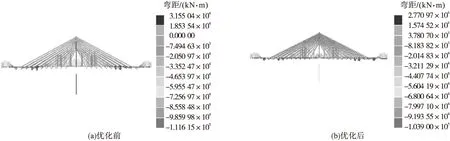
图5 优化前后恒载作用下的弯矩图Fig.5 Bending moment under the constant load before optimization and after optimization

图6 优化前后主+附作用下的弯矩图Fig.6 Bending moment under the main,additional load before optimization and after optimization

从图5可以看出，主梁最大负弯矩出现在1/4跨处，主梁最大正弯矩出现在跨中处。可以看到在恒载作用下优化前最大弯矩值为31 550 kN·m，优化后最大弯矩值为27 709 kN·m，降低了12.17%；优化前最小弯矩值为-111 615 kN·m，优化后最小弯矩值为-103 900 kN·m，绝对值降低了7.42%；优化前跨中弯矩值为22 724 kN·m，优化后跨中弯矩值为20 980 kN·m，减低了7.67%。从图6可以得出，在恒载、活载、温度、横向风荷载同时作用下，主梁的正负弯矩值都有一定量的增加，同时因为矮塔斜拉桥在活载作用的影响，塔根负弯矩会比较大。通过索力优化，在主力+附加力作用下的塔根负弯矩从-276 622 kN·m减少到-229 586 kN·m，降低了16.96%，最大弯矩值也从优化前的88 929 kN·m减少到81 865 kN·m，降低了7.94%。分析表明，通过优化，主梁最大正负弯矩绝对值以及各处弯矩值都有一定程度的降低，主梁弯矩图也变得更加均匀。

3.3 主梁挠度结果对比

在自重和斜拉索竖向分力作用下，矮塔斜拉桥的主梁位移以竖向挠度为主，以主塔为中心线，索力优化前后主梁挠度对比如图7所示。

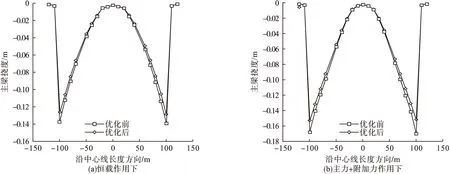
图7 优化前后恒载作用和主+附作用的挠度对比图Fig.7 Comparison of deflection under the constant load and main,additional force before optimization and after optimization

从图7可以看出，在恒载作用下，主梁位移方向为竖直向下，同时主梁竖向最大位移发生在两端的最大悬臂端附近。优化前主梁竖直方向的最大位移为-0.139 m，优化后主梁竖直方向的最大位移为-0.123 m，最大位移量降低了11.51%。在主力+附加力作用下，由于受到恒载、活载、温度、横向风荷载的共同作用，主梁的竖向位移均有所增加。优化前竖直方向的最大位移为-0.169 m，优化后竖直方向的最大位移为-0.151 m，最大位移量减低了10.651%。因此可以看出，无论从恒载作用下还是从主力+附加力作用下的优化前后主梁挠度均可以得出，通过索力优化可以改变矮塔斜拉桥局部线形的变化情况，从而使主梁更接近理想成桥状态。

3.4 主梁应力结果对比

恒载作用下优化前后矮塔斜拉桥的应力如图8所示，主力+附加力作用下优化前后矮塔斜拉桥的应力如图9所示。

图8 优化前后恒载作用下的应力图Fig.8 Stress under the constant load before optimization and after optimization

图9 优化前后主+附作用下的主梁应力图Fig.9 Stress under the main,additional force before optimization and after optimization

从图8可以看出，在恒载作用下，优化前后的主梁均为压应力，主塔也呈全截面受压状态。主梁的最大压应力在最大悬臂端处，最小压应力在两端边墩处，而主塔的最大压应力位于塔梁固结的地方。优化前主梁最大压应力为12.99 MPa，优化后主梁最大压应力为11.79 MPa，降低了9.23%；优化前主塔的最大压应力为6.94 MPa，优化后主塔最大压应力为6.38 MPa，降低了8.06%。从图9可以看出，在主力+附加力作用下，矮塔斜拉桥整体结构状态同样为全截面受压。优化前主梁最大压应力为14.85 MPa，优化后主梁最大压应力为12.61 MPa，降低了14.99%；优化前主塔最大压应力为7.43 MPa，优化后主塔最大压应力为6.87 MPa，降低了7.53%。分析可知，索力优化可以有效地降低矮塔斜拉桥整体结构的应力状态，使应力分布更加均匀，应力状态满足材料容许的应力要求。

4 结 论

(1) 在进行矮塔斜拉桥拉索索力优化过程中，通过恒载作用下的索力和主力+附加力作用下的优化结果对比可以看出，活载、温度荷载、横向风荷载对于索力的影响比恒载对索力的影响要小，因此可以从恒载的角度考虑成桥索力优化。

(2) 索力优化后，主梁最大正负弯矩绝对值以及各处弯矩值均有一定程度的降低，主梁弯矩图也变得更加均匀，避免出现桥梁个别截面内力过大的情况。

(3) 索力优化可以改变矮塔斜拉桥局部线形的变化情况，从而使主梁更接近理想成桥状态。

(4) 索力优化可以有效地降低矮塔斜拉桥整体结构的应力状态，使应力分布更加均匀，应力状态满足材料容许的应力要求。