一维周期晶格与准周期Harper链耦合系统的电子性质研究*

蒋金益，王 超，陆艳艳，钟建新

(湘潭大学 物理与光电工程学院 微纳能源材料与器件湖南省重点实验室，湖南 湘潭 411105)

0 引言

自1958年在无序系统发现安德森转变[1]以来，低维量子系统中波函数的局域化问题引发科学界的大量关注，并在实验和理论方面展开深入研究[2].安德森的局域化表明，单粒子波函数在具有不相关随机无序的体系中发生局域化[3]，导致金属-绝缘体转变，其原因来自随机杂质和缺陷粒子散射过程中的量子干涉效应[4].研究发现[1-4]，一维和二维无序系统中的全部电子态都是局域态，而三维无序系统中存在金属-绝缘体转变现象.在三维无序系统中，带中态为扩展态，带尾态为局域态，扩展态与局域态之间存在迁移率边，其本征态为临界态；随着无序强度的增大，局域态区不断扩大，而扩展态区不断缩小，并在无序大于临界无序强度时，扩展态消失，系统中所有的态为局域态，发生金属-绝缘体转变.虽然标准的安德森转变是在三维系统中发生，但是在准无序的一维系统中也有类似的转变.最典型的模型是一维准周期Harper链或Aubry André Harper模型[5]，它可通过调节格点能的准周期调制势，使电子态呈现出扩展态、临界态和局域态，产生金属-绝缘体转变[6].Harper链模型被广泛应用于指数短程跳跃效应[7]、平带网络模型[8]、幂指数跳跃效应[9]、以及二维晶格中的磁场效应[10]等方面.此外，实验上对Harper模型的研究也有所突破[11]，采用冷原子和光晶格，发现了理论预言的金属-绝缘体转变[12]；Bloch等[13]最近通过冷原子和光波导在一维双色准周期Harper系统中观测到了具有迁移率边的金属-绝缘体转变.

近年来，有研究者将两个或多个耦合链进行研究.钟建新等[14]研究了准一维周期晶格纳米线与无序体系的耦合，发现该耦合体系中存在类似于Anderon局域化的准迁移率边和准金属-绝缘体转变现象，并在二维无序-有序耦合体系中发现了持续存在的迁移率边和金属-绝缘体转变[15].这一反常现象引起了对一维周期链与无序链耦合双链模型的进一步研究[16]，在耦合的Harper双链模型中发现了金属-绝缘体转变和迁移率边[17].然而，已有一维准周期双链耦合系统的研究仅关注同类体系的耦合效应，没有系统性地深入探讨准周期链的调制势和链间耦合强度对一维周期晶格电子性质的影响.

在本文中，基于紧束缚哈密顿量，研究由一维周期晶格与准周期Harper链耦合形成的双链耦合系统的电子局域化性质.通过调节Harper链中的格点位能调制势以及双链间的耦合作用强度，计算耦合体系的本征能量与本征波函数，分析波函数的扩展和局域化特性，以及电子扩散中波函数和扩散距离随时间变化的规律，探究Harper势和链间耦合强度对耦合系统电子性质的调控效应.该研究对深入了解和调控低维系统的电子局域化性质具有重要意义，同时对冷原子局域化的实验研究具有指导意义.

1 模型及理论推导

一维周期晶格中的电子态全部是扩展态，而一维Harper链可通过改变格点位能的调制势使电子态呈现出扩展态、临界态和局域态，即出现金属-绝缘体转变.研究一维周期晶格与Harper链耦合形成的双链耦合模型，如图1所示，探究改变Harper势和链间耦合作用对该耦合系统电子性质的影响.

图1 一维周期晶格与准周期Harper链耦合系统示意图Fig.1 Schematic diagram of the coupled system with one-dimensional periodic lattice and Harper chain

考虑一个格点数为N的双链耦合系统，其中周期链和Harper链的格点数分别为N/2，系统的紧束缚哈密顿量[18]为：

(1)

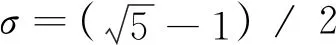
(2)

式中，Ψ(t)=(…,ψn-1,ψn,ψn+1,…)T表示在t时刻的波函数，ψn(t)表示第n个格点处Ψ(t)的系数.初始条件为：

|ψn(t=0)|=δn,0.

(3)

具有初始条件(3)的式(2)可采用有限时间步长Runge-Kutta方法或通过如下静态薛定谔方程求解，

HΦ(E)=EΦ(E) .

(4)

式(4)中，E代表本征能量值，Φ(E)表示本征态波函数，Φ(E)=(…,φn-1,φn,φn+1,…)T.通过求解(4)可得到所有的本征能量Ej(j=1,2,…,N)和相应的本征态Φ(Ej).因为Φ(Ej)是正交完备集，则可将波函数Ψ(t)表示为：

(5)

由初始条件(3)可知：

(6)

将(6)式代入(5)则可得到完整的波函数表示为：

(7)

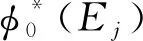
用数值方法来研究有限大小的系统，由于仅关注波函数长时间未到达边界的变化情况，在计算中采用固定边界条件.采用波包的均方位移d(t)来描述电子的扩散情况.

(8)

2 结果与分析

2.1 耦合系统中电子波函数随时间的演化

利用矩阵三对角化数值求解公式(4)，得到本征能量和本征波函数，通过公式(7)进一步计算得到随时间变化的波函数.以周期晶格(u=0)与Harper链(λ=3)耦合系统的电子波函数为例来分析耦合系统中波函数随时间的演化特点，如图2所示.图2(a)和(b)分别为链间耦合为R=1时，周期链中和Harper链中电子波函数平方随时间的变化情况.对比图2(a)和(b)可以发现，在同一时刻，电子波函数在周期链中扩展较快，而在Harper链中电子仅有部分扩展.图2 (c) 和(d)分别为R=3时电子在周期链中和在Harper链中的扩展情况.通过对比图2(b)和(d)，可发现当链间耦合作用增大时，电子在Harper链上的扩展比R=1时更多.出现这种情况的原因是，当链间耦合能增大时，电子在周期链和Harper链中上下跳跃频繁，又因电子在周期链上做无阻碍运动，进而使得更多的电子能够在双链上扩展出去.这一现象也存在于具有其他Harper势参数的双链耦合系统.

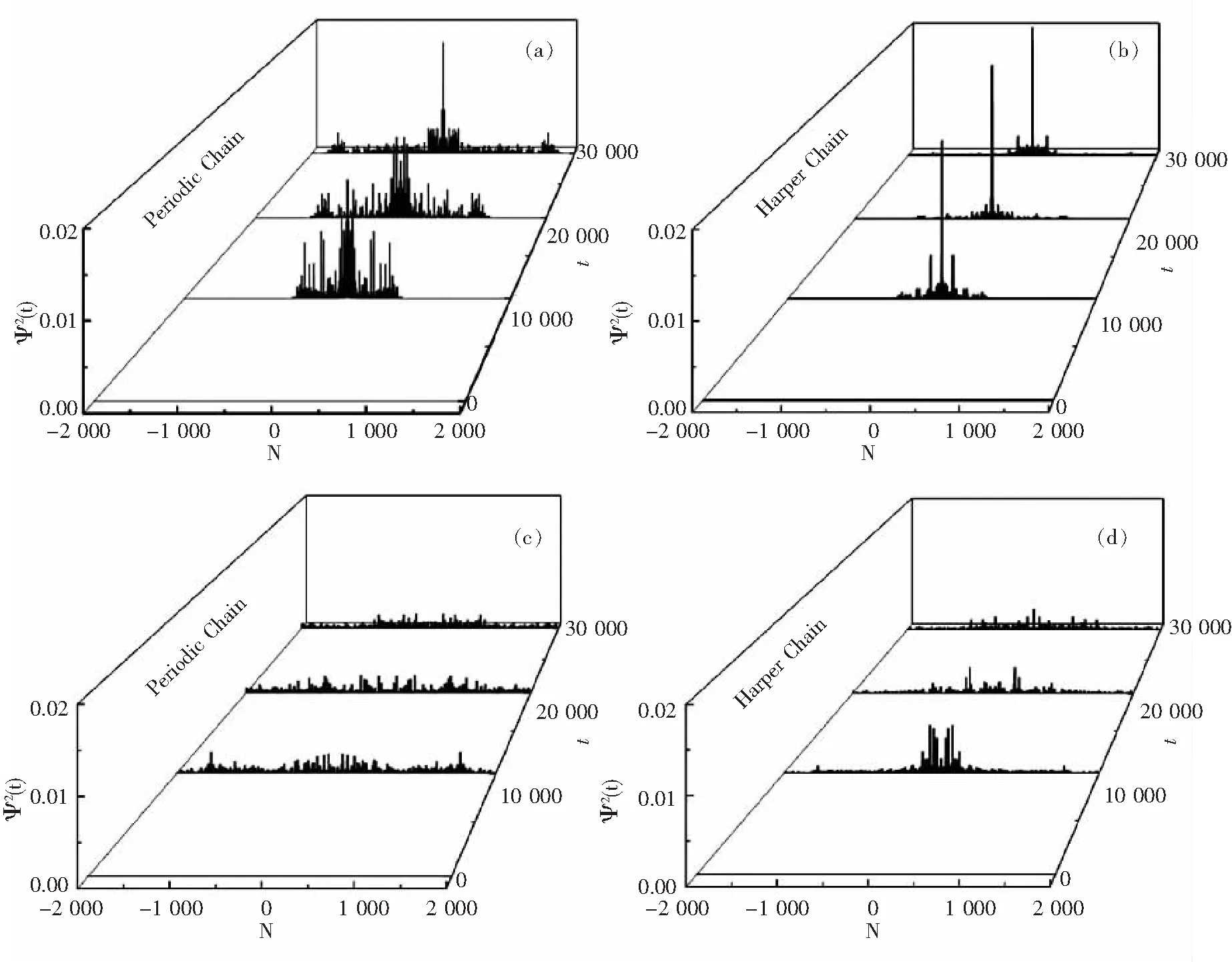
图2 周期链(u=0)与Harper链(λ=3)耦合系统的电子波函数随时间演化图图2(a)、(b)中的链间耦合作用为R=1；(c)、(d)中的链间耦合作用为R=3.Figure 2 Time evolution of the electronic wavepacket in the coupled system with periodic chain (u=0) and Harper chain (λ=3).Fig 2(a) and 2(b) are for the interchain coupling R=1.0. Fig 2(c) and 2(d) are for the interchain coupling R=3

.

2.2 耦合系统的本征波函数特性

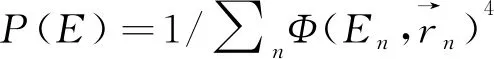
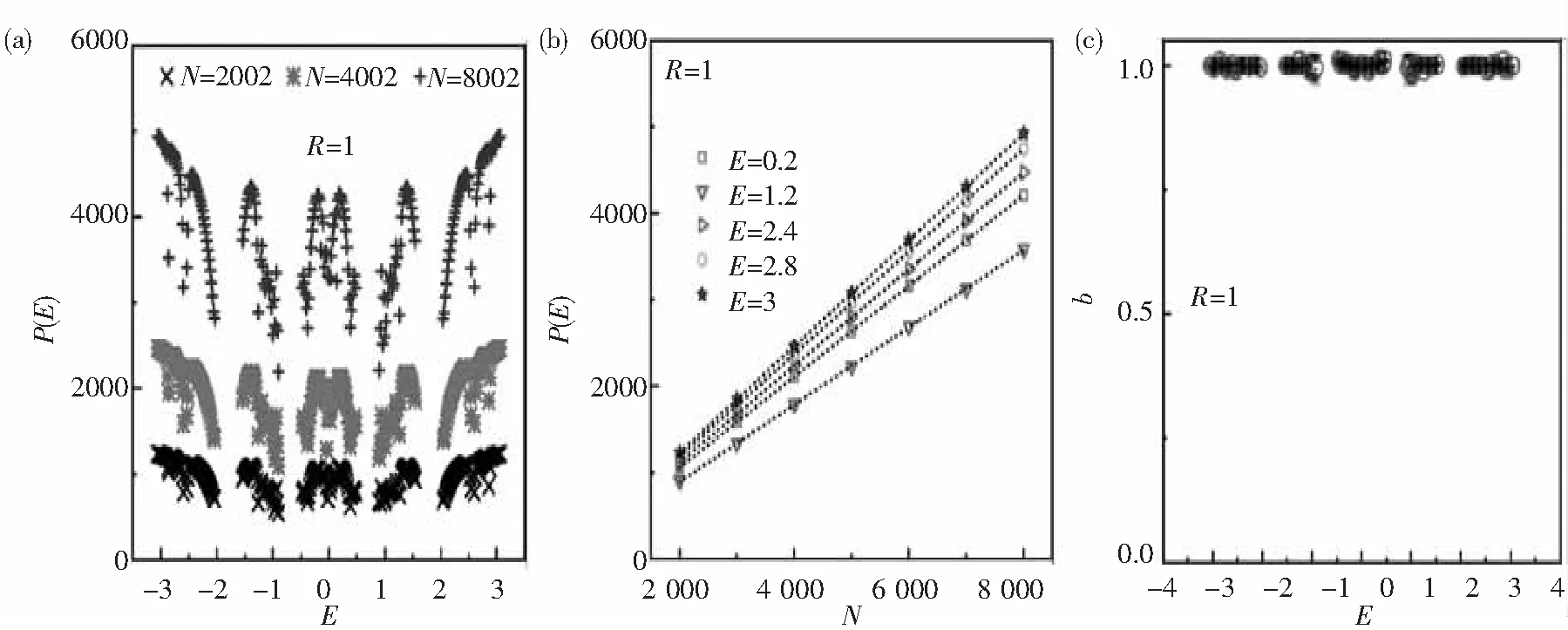
图3 周期链(u=0)与Harper链(λ=1)耦合系统的参与数P(E)，其中链间耦合为R=1. (a)不同系统尺寸N的P(E)分布图；(b)典型能量处P(E)与N的线性递增关系；(c)拟合幂指数b分布图.Fig.3 The participant number of the coupled system with periodic chain (u=0) and Harper chain (λ=1) with interchain coupling R=1. (a) P (E) values for different system sizes. (b) Linear behaviors of P (E) as N increases at selected energies. (c) Distribution of exponent b for the power-law increase

图4 周期链(u=0)与Harper(λ=2)链耦合双链的参与数，其链间耦合分别为R=0.5，1，3. (a)不同系统尺寸N的P(E)分布图；(b)典型能量处P(E)与N的线性递增关系；(c)拟合幂指数b分布图.Fig.4 The participant number of the coupled system with periodic chain (u=0) and Harper chain (λ=2) with different interchain coupling R=0.5, 1, 3. (a) P(E) values for different system sizes. (b) Linear behaviors of P(E) as N increases at selected energies. (c) Distributions of exponent b for the power-law increase

图5 周期链(u=0)与Harper链(λ=3)耦合双链的参与数P(E)，其中链间耦合分别为R=1，2，3. (a)不同系统尺寸N的P(E)分布图；(b)典型能量处P(E)与N的线性递增关系；(c)拟合幂指数b分布图.Fig.5 The participant number of the coupled system with periodic chain (u=0) and Harper chain (λ=3) with different interchain coupling R=1, 2, 3.(a) P(E) values for different system sizes. (b) Linear behaviors of P(E)我们仅 as N increases at selected energies. (c) Distributions of exponent b for the power-law increase

2.3 耦合系统中的量子扩散

通过电子的均方位移d(t)来研究电子在双链中的量子扩散情况[19].周期晶格与Harper链(λ=1，2，3)耦合系统下的均方位移如图6所示，其中双链耦合作用分别为R=0.1，0.5，1，2，3.由于耦合系统在任何非零耦合强度下均存在扩展态，其量子扩散整体上均表现为弹道式扩散，即扩散距离正比于时间，但其扩散速率受调制势和耦合作用的影响，如图6所示.经计算电子扩散到达边界的时间，并选取波包未达到边界前的数据进行拟合，得到扩散距离d(t)的斜率(速率)与耦合能R的关系图，如图6中内插图所示.从图6可以清楚地看出，对于不同的Harper链调制势，扩散速率随耦合能增加均呈现出从先减少再到提高至一个稳定速率的变化过程.当链间耦合较小时(R=0.1)，电子扩散很快；随着耦合作用增强，电子扩散逐渐变慢并在R=1时达到最小；当链间耦合作用继续增大时，电子扩散变快，并在耦合能增大至R=3后趋于稳定.产生这一转变的原因是，随着链间的耦合作用逐渐增大，电子从周期链跳跃到Harper链的可能性增强，使其扩散速率因Harper势的阻碍而变慢；但当链间耦合作用继续增大时，Harper链上的电子扩散至周期链的概率大幅增加，电子在双链上下频繁跳跃扩散，最后以稳定的速率进行扩散运动.

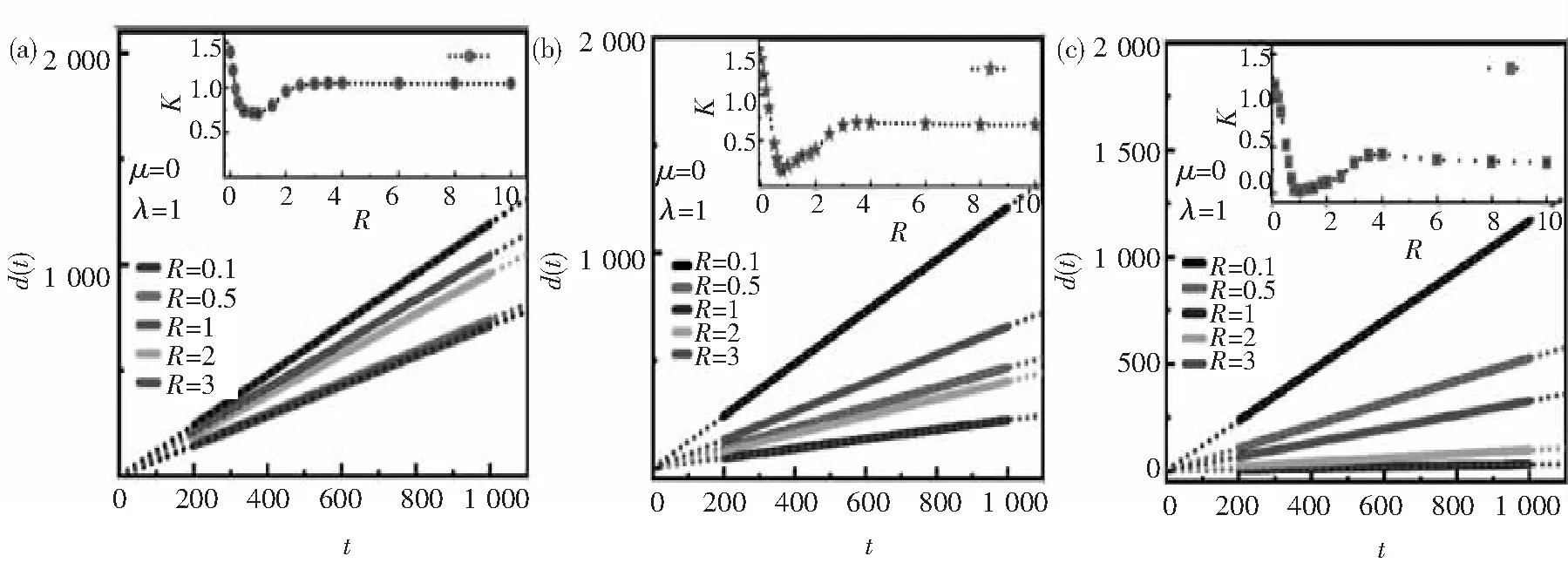
图6 周期链(u=0)与Harper链(λ=1，2，3)耦合系统在不同耦合强度R时的电子波包扩散均方位移d(t). 内插图为d(t)的斜率k与链间耦合作用R的关系.系统大小为N=8002.Fig.6 The mean square displacement of the wavepacket in the coupled system with different Harper potentials λ and different coupling strengths. The inset shows the relationship between the slope of d(t) and the interchain coupling R. The size of the system is N=8002

3 结论

提出了一维周期晶格与准周期Harper链耦合形成的双链耦合紧束缚模型，通过数值求解，计算出电子的本征态能量与波函数，并通过分析本征波函数的参与数随体系尺寸的变化规律，以及电子波函数和均方位移随时间的演化特征，研究准周期Harper势和链间耦合强度对周期晶格电子性质的调制效应.发现该耦合系统具有丰富的电子性质：1)无论Harper势处于扩展态区、临界态区还是局域态区，电子波函数在周期链和Harper链中均有不同程度的扩散，在周期链上扩展较快，而在Harper链上电子仅有部分扩展；增大链间耦合强度时，电子在Harper链上扩展范围更大；2)不同Harper势情况下，耦合体系的本征电子态可出现扩展态、临界态和局域态，并且随着链间耦合能的增大，电子态发生由局域态向临界态和扩展态的转变；当Harper势处于扩展态区时，耦合体系的全部电子态为扩展态；当Harper势处于临界态区时，弱耦合体系中扩展态与临界态并存，强耦合体系中的全部电子态为扩展态；当Harper势处于局域态区时，弱耦合体系中扩展态、临界态、局域态并存，临界态和局域态随耦合强度增加逐渐消失，强耦合体系中的全部电子态为扩展态；3)由于扩展态的贡献，无论Harper势参数如何改变，电子都以弹道式的方式扩散，但由于Harper势的阻碍以及电子在周期链与Harper链之间的频繁跳跃，其速率随链间耦合能的增大呈现出先减小后逐渐增大直至不变的转变.