基于树突网络的侧信道攻击*

王俊年，王 皖，于文新，胡钒梁

(1.湖南科技大学 物理与电子科学学院，湖南 湘潭 411201;2.智能传感器与新型传感材料湖南省重点实验室，湖南 湘潭 411201;3.湖南省教育厅知识处理与网络化制造重点实验室，湖南 湘潭 411201)

0 引言

在过去的几年中，侧信道攻击(Side-Channel Attack, SCA)技术已经被证明是实现加密算法密钥攻击恢复的一种有效方法[1].现实中，由于加密设备在运行加密算法的时候，不可避免地会有一些物理信息的泄露，例如电磁、功耗和时间等信息泄露，所以可以通过示波器等设备获取到该加密设备的相关泄露信息，从而恢复出加密设备的密钥信息.

由于深度学习模型对数据特征很敏感，具有从原始数据中学习并提取数据内在特征的能力，因此，将深度学习算法应用于加密硬件芯片的侧信道信号分析，提高侧信道分析的效率是自然而然的事情.近年来，已经有多种基于深度学习的侧信道分析方法被提出[2-3]，例如，Maghrebi等[4]在2016年首次将深度学习技术应用与侧信道攻击，并使用多层感知机(Multilayer Perceptron, MLP)和卷积神经网络(Convolution Neural Network, CNN)模型实现了密钥的恢复；Cagli等[5]提出了一种基于卷积神经网络的端到端的建模类侧信道攻击方法，这种方法不需要对功耗数据曲线进行前期的预处理，也不需要精确的兴趣点区间，此外，他们还使用数据增强技术提升了卷积神经网络的性能，并通过实验评估了CNN网络在处理抖动数据集时的性能情况；Robyns等[6]最近提出了一种新的相关优化(Correlation Optimization, CO)方法，在所有的电磁数据中选择有用的泄露样本作为机器学习的输入数来改进相关电磁分析(Correlation Electronmagnetic Analysis, CEMA).除此之外，还有多个其他的深度学习侧信道攻击工作，例如，文献[7]通过使用多种深度学习模型进行侧信道攻击实验，表明了侧信道攻击中目标加密芯片的多样性对实验结果的影响；文献[8]基于几种不同的微系统架构和实验环境，提出了一种基于黑盒的侧信道分析系统ABSynthes，并通过循环神经网络(Recurrent Neural Network,RNN)模型的分类实验，成功实现了所有比特流密钥的恢复.这些研究工作表明，基于深度学习的侧信道分析在密钥攻击效率和准确性等方面都有良好的表现.

深度学习网络虽然用更深的神经网络结构模型逼近目标的非线性特征，但由于其神经元采用非线性激活函数，仍然是一个非线性结构未知的黑盒模型，在训练过程中不可避免地存在过拟合和局部最优的问题，训练获得的模型结构和性能不一定是最优.树突网络(Dendrite Detwork, DD)是最近提出的一种精度可控、泛化能力强、复杂度比较低的机器学习算法[9-10].树突网络通过设计没有非线性激活函数的“透明”网络，在保留人工神经网络出色的非线性逼近能力的情况下，可以解释网络的内部非线性结构，是一种“白盒”机器学习模型，在系统辨识、计算复杂度等方面有很好的表现.本文将树突网络应用于侧信道分析，提出一种基于树突网络的深度学习侧信道分析方法，并与基于多层感知机、卷积神经网络、循环神经网络的侧信道分析分别进行实验对比，实验结果表明，基于树突网络的模型在模型总参数规模、验证精度、训练时间和预测可靠性等方面都要优于另外三个模型.

1 侧信道攻击

1.1 AES高级加密标准

高级加密标准(Advanced Encryption Standard, AES)是目前应用最为广泛的对称分组加密算法，由美国国家标准技术研究所在2001年发布[11-12].根据加密操作时使用的密钥长度不同，AES又被分为AES-128、AES-192和AES-256三种加密算法.本文中使用的加密算法是AES-128，攻击的目标是AES-128加密算法的初始密钥.AES-128加密算法一共包括了10轮加密操作，分组密钥块的长度是128比特，即16个字节.除最后一轮外，其余每一轮都包含四个基本的加密操作，分别是字节替换(SubBytes)、行移位(ShiftRows)、列混淆(MixColumns)和轮密钥加(AddRoundKey)，而最后一轮不包含列混淆操作.在AES-128加密算法中，唯一的非线性变换就是S-box的字节替换，经过S-box的操作，能够很大程度地保证整个加密算法的安全性.对于一组密钥所有的16个字节，文中的攻击策略是对每个字节进行逐一破解，最终实现所有字节密钥的恢复.

1.2 模板型能量分析攻击

模板型的侧信道能量分析攻击被普遍认为是最为强大的侧信道攻击技术，这种攻击方法一般分为两个阶段：第一阶段(分析阶段)，攻击这拥有一个与目标加密设备完全相同的可编程加密设备，并且攻击者可以通过此设备很精确地提取目标加密芯片的物理泄露信息.假设攻击者通过该设备一共获取了Np条功耗泄露数据Xprofiling，用集合Xprofiling= {xi|i=1,2,…,Np}表示，其中xi表示第i条功耗数据向量.设vi=g(ti,k*)是一个随机变量，用来表示第i条功耗数据xi对应固定密钥k*时的加密操作中间值，其中ti表示第i个明文或密文块，k*∈K表示第i条功耗数据xi对应的固定密钥，K表示0～255的密钥空间，于是，攻击者可以通过建模集合{xi,vi}i=1,2,…,Np进行建模，并计算条件概率：

Pr[x|V=v].

(1)

第二阶段(攻击阶段)，攻击者从实际目标设备(在结构上与分析阶段加密设备相同)生成Na条新的功耗曲线，用集合Xattack= {xi|i= 1, 2,… ,Na}表示.此时的Xattack和Xprofiling是相互独立的，并且每条功耗曲线对应的密钥k*都是固定和未知的.为了恢复未知的固定密钥，对所有可能的候选密钥k∈K进行中间值的计算，然后根据贝叶斯定理计算每一条能量曲线xi对应猜测密钥k时的加密操作中间值的后验概率：

(2)

式中g(ti,k)表示对应能量曲线xi时对猜测密钥k进行加密操作的中间值状态；g(·)表示公共信息ti和猜测密钥k进行中间值计算时的操作函数.最后对公式(2)按照最大似然函数的策略进行计算：

(3)

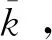
1.3 实验评价指标

本实验将使用两个评价指标来对各个实验模型进行评估分析：

(1)模型精度和损失.

模型精度指的是模型在验证集上取得正确分类结果的概率[13].模型精度是机器学习中一种最常用的模型评价指标，用来表征模型对数据的分类能力.模型精度的提高表明了反向传播算法对权重和偏置参数的优化逐渐收敛靠近最优的参数值，网络模型也逐渐收敛到最优模型.模型的精度一般可以定义成：

(4)

模型的损失表征了一个模型的预测值与真实值之间的偏差程度，损失值越小，模型的预测结果越靠近真实值，模型的预测可靠性越高，鲁棒性越强.本文实验使用交叉熵损失函数categorical crossentropy来计算模型的损失值并通过反向传播来优化模型的权重和偏置参数.

(2)模型参数和训练时间.

模型的参数一般指模型内部的配置变量，可以通过数据来估计模型参数的规模.在保证模型的精度相同的情况下，如果一个模型的总参数越少，则该模型的结构就越精简，模型训练所占用的内存资源更少；如果一个模型的训练时间越短，则表明该模型的性能越好，模型收敛速度更快，更容易进行深度学习训练.

2 基于树突网络的侧信道攻击

2.1 DD模型简介

传统的机器学习算法在处理分类问题时，主要是根据数据本身的特征去划分数据，基本原则都是去找到一个合适的分类曲线或者曲面去解决这个分类问题.但是基于这种策略的机器学习算法实际上生成了一个黑盒模型，而树突网络(DD)是一种计算复杂度较低的白盒算法，它可以通过提取输入数据之间的逻辑关系信息来实现分类任务，而不用去寻找分类曲线或曲面.DD模型的结构很简单，其基本结构如图1所示.DD模型的一个基本结构可以表示如下：

图1 DD模型基础模块Fig.1 Basic module of DD model

Al=Wl,l-1Al-1∘X.

(5)

式(5)中:Al和Al-1分别表示第l个DD模块的输出和输入；X表示DD的输入；Wl,l-1表示从第l个模块到第l-1个模块的权重矩阵；“∘”表示哈达玛积.DD结构的本质是，如果输出的逻辑表达式中包含输入数据之间对应分类的逻辑关系(与、或、非)，则该算法的模型就可以提取输入数据之间的逻辑关系信息，然后通过训练学习这种逻辑关系并实现分类任务.

2.2 DD模型的基本学习策略

DD模型的基本学习策略如图2所示.例如，假设我们使用均方误差(MSE)的一半作为模型的损失函数，则可以推理出基于DD模型的误差反向传播的学习规律[14]：

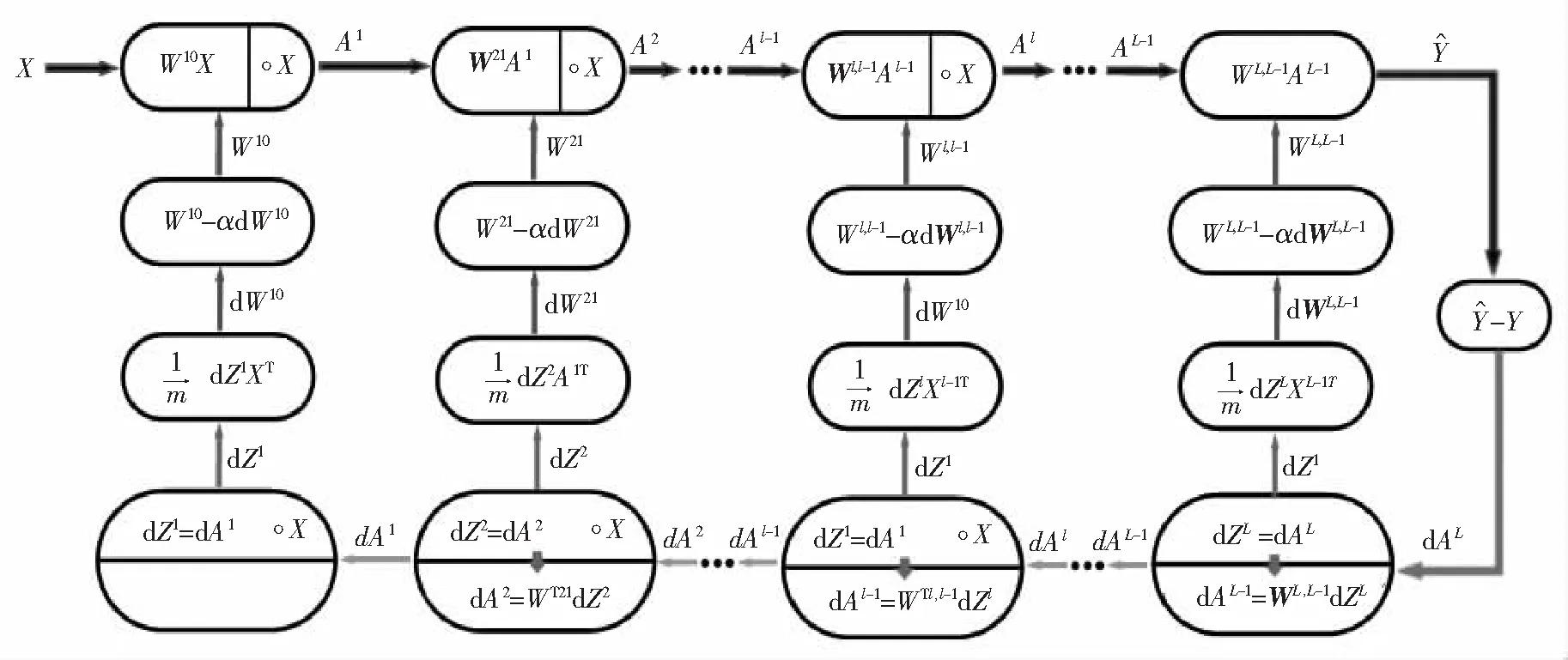
图2 DD模型的基本学习策略Fig.2 Basic learning strategy of DD model

(1) DD模块和线性模块的正向传播：

(6)

(2) DD模块和线性模块的误差反向传播：

(7)

(8)

dAl-1=(Wl,l-1)TdZl.

(9)

(3) DD模型的权重优化：

(10)

2.3 基于DD模型的侧信道攻击

图3展示了基于DD模型的侧信道攻击主要流程，具体步骤如下：

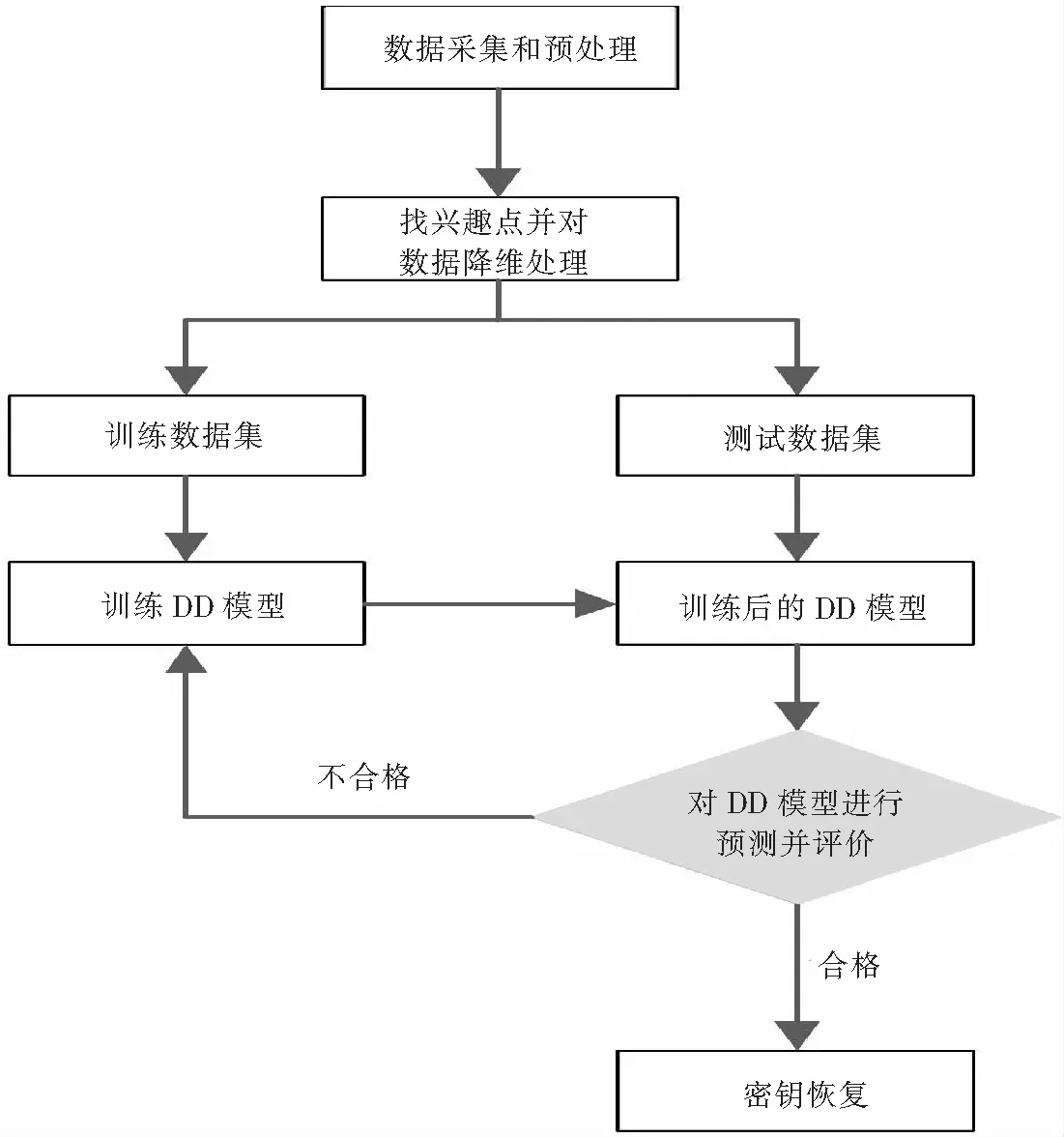
图3 基于DD模型的侧信道攻击流程Fig. 3 SCA process based DD model

(1) 数据集的采集和预处理.本实验中，通过ChipWhisperer平台分别对加密板A和B采集60 000条和150 000条侧信道功耗数据，在采集到足够的数据后，首先要对原始数据进行预处理操作，然后再分别对每一组数据集进行随机划分训练集和测试集.

(2) 选择兴趣点.选择兴趣点的主要目的是为了减少与目标字节无关的加密操作信息，加强目标字节的加密操作信息特征.实验中通过CPA的方法寻找目标字节的兴趣区间，然后选取出兴趣区间内的数据作为降维后的新数据，并传送给网络模型进行特征提取和学习.

(3) 模型训练.在采集到加密板A和B上的功耗数据后，首先根据两组数据的特征，分别确定对应数据集的DD模型具体结构，然后再使用划分出来的训练集对DD模型进行训练优化.在本实验中，两个DD模型的输入神经元分别设置为150和130，隐藏层的神经元数也与输入层保持一致，模型的全局优化器分别设置为Adam和RMSprop.

(4) 模型测试.在DD模型训练完成后，使用对应的测试数据集对模型进行评估.在本文中主要通过模型的精度、损失、参数规模、训练时间和模型的计算复杂度等指标来对模型进行评估.

(5)密钥恢复.对于密钥的恢复，使用“分而治之”的策略，对AES-128加密算法的初始密钥块进行16个字节的逐一恢复.恢复密钥的基本过程是通过评估的最优DD模型，预测出要恢复的密钥字节对应的中间值状态(即S-box的输出状态，一共有28=256种.)，然后结合已知的明文信息对中间值状态进行逆向计算，从而恢复出目标字节的密钥信息.

3 实验和模型评估

3.1 实验环境配置

本文所有实验都是在相同的实验环境配置下完成的.实验中使用ChipWhisperer[15]加密设备以40 MHz的采样频率采集功耗数据，图4展示了实验设备和数据集的采集过程.图5是本文实验的两块目标加密板，目标加密板A的型号是CW308T-STM32F3，上面搭载了一块32-bit Arm Cortex-M4加密芯片；目标加密板B的型号是ATXmega128D4-AU，上面搭载的是8bit ATMEL微控制器，两块目标加密板中实际运行的加密算法均是TinyAES-128C[16]，加密模式则是电码本(ECB)的模式.本次实验所有模型的搭建和训练都是在深度学习框架Keras-gpu 2.3.1和tensorflow-gpu 2.1.0下进行的；计算机主要硬件配置为一块Intel(R) Core(TM) i5-8400 CPU @2.80GHz CPU和一块NVIDIA GeForce GTX 1060 6GB GPU，完成实验中所有的数值计算和模型训练工作.

图4 使用ChipWhisperer设备采集功耗数据 图5 加密板A和加密板BFig.4 Collect power consumption data with ChipWhisperer Fig.5 Encryption board A and encryption board B

3.2 数据采集和预处理

本次实验中，首先针对加密板A进行数据采集工作，一共采集到了60 000条能量曲线用作实验数据集，加密设备在整个加密过程中都是使用随机明文和固定密钥进行加密.对实验中采集到的能量曲线，在进行对齐处理后，将其中的50 000条划分为训练数据集，并随机从训练集中留出5 000条数据进行验证，最后将剩下的10 000条划为测试数据集.实验中的每一条功耗trace都包含了3 000个采样点.图6是从加密板A上采集的原始能量迹曲线波形，其中图(a)为第一轮加密时所有操作的功耗信息曲线波形，包含了轮密钥加、字节替换、行移位和列混淆加密操作信息；图(b)是针对第一轮S-box字节替换操作的功耗曲线图.

(a) 单条能量迹曲线波形 (b) S-box能量迹曲线放大波形图6 加密板A采集的原始功耗曲线Fig.6 Raw power consumption curve collected by encryption board A

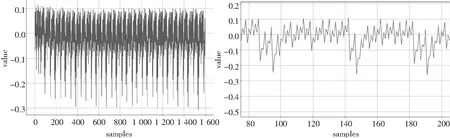
(a) 单条能量迹曲线波形 (b) S-box能量迹曲线放大波形图7 加密板B采集的原始功耗曲线Fig. 7 Raw power consumption curve collected by encryption board B

针对加密板B，一共采集了150 000条功耗数据，其中100 000条是用随机密钥进行加密获得的，作为实验的训练集，并从其中随即划分10 000条作为验证数据集；另外50,000条是用固定密钥加密采集的数据，作为本实验的测试数据集.图7是从加密板B上采集的原始能量迹曲线波形，其中图(a)为第一轮加密时16个S-box操作所对应的能量迹曲线；图(b)是第一个S-box操作的能量迹曲线放大后的图形.

3.3 攻击点和兴趣区间

3.3.1 攻击点的选择

在实施侧信道攻击时，研究人员首先需要对加密设备在运行加密算法时的能量消耗进行建模，而一般主要有三种能量模型，分别为身份模型(ID模型)、汉明距离模型(HD模型)和汉明重量模型(HW模型)，对于不同的能量消耗模型，功耗数据的标签也有所不同.本文选择的是ID模型，对应的标签种类一共有28=256种.

在确定能量消耗模型后，需要确定目标攻击点的位置.本文针对的加密算法是AES-128，选择的目标攻击点是该加密算法的第一轮加密操作中字节替换的输出位置(即S-box的输出).侧信道攻击实验最终目标是恢复出初始密钥块的第一个字节，用k0表示.把实验中各个模型训练的标签都设置为第一轮加密操作中S-box字节替换的输出状态，表示为：

state0=Sbox(p0⊕k0)，

(11)

式中：“⊕”表示的是按位异或操作；p0和k0分别表示明文的第一个字节和初始密钥的第一个字节；state0表示经过S-box输出后的状态，即标签.这样设置标签的主要原因是目标加密芯片在运行加密算法的时候，首先需要从内部的寄存器中调用S-box去执行加密算法中的字节替换操作，然后再将操作后的中间状态加载到数据总线上，而数据总线的电容负载一般很大，对加密芯片的能量消耗有很大的影响.

3.3.2 兴趣点的选择

由于实验的目标攻击点是第一轮加密操作中S-box字节替换后的输出位置，而此位置一共包含了16个字节的S-box输出信息，所以需要找到目标字节(第一轮S-box输出状态的第一个字节)的泄露信息区间(兴趣区间).

使用CPA技术寻找目标字节的兴趣区间[17]，主要分析步骤如下：

(1) 利用功耗采集设备采集原始功耗数据，并对齐所有数据；

(2) 使用公共信息(明文或密文)和所有可能的密钥进行S-box的字节替换操作，通过计算得到中间值矩阵；

(3) 使用CPA方法计算中间值矩阵和原始功耗数据之间的pearson相关系数，并选出相关系数最大的区间，即兴趣区间；

(4) 对所有的原始功耗数据进行降维处理，只保留兴趣区间内的功耗数据信息.

实验中对两块加密板的功耗数据分别进行CPA分析，最后结果如图8所示，其中黑色虚线的范围就是本文实验中目标字节的区间.

(a)加密板A的CPA结果 (b) 加密板B的CPA结果图8 CPA计算结果Fig. 8 CPA calculation result

3.4 对加密板A的侧信道攻击实验

首先针对加密板A进行侧信道实验.实验中，DD模型一共有6层，其中三层是DD基础模块结构，输入层和所有隐藏层神经元数目均设置为输入数据的特征个数，即150个；模型的优化器设置为Adam，对应的学习率大小设置为0.000 1；所有网络层的use_bias参数均设置为False，即不使用层偏置向量；输出层使用softmax激活函数，而其余的网络层均不设置激活函数.最后整个DD模型的参数一共有128 400个，具体的模型参数如表1所示.

表1 DD模型结构参数

由于DD模型结构不使用激活函数和偏置项，神经网络在前向传播和反向传播时模型参数的计算复杂度大大降低，因此相比较于其他的模型，DD模型会更高效.DD模型分类实验的最终结果如图9所示.

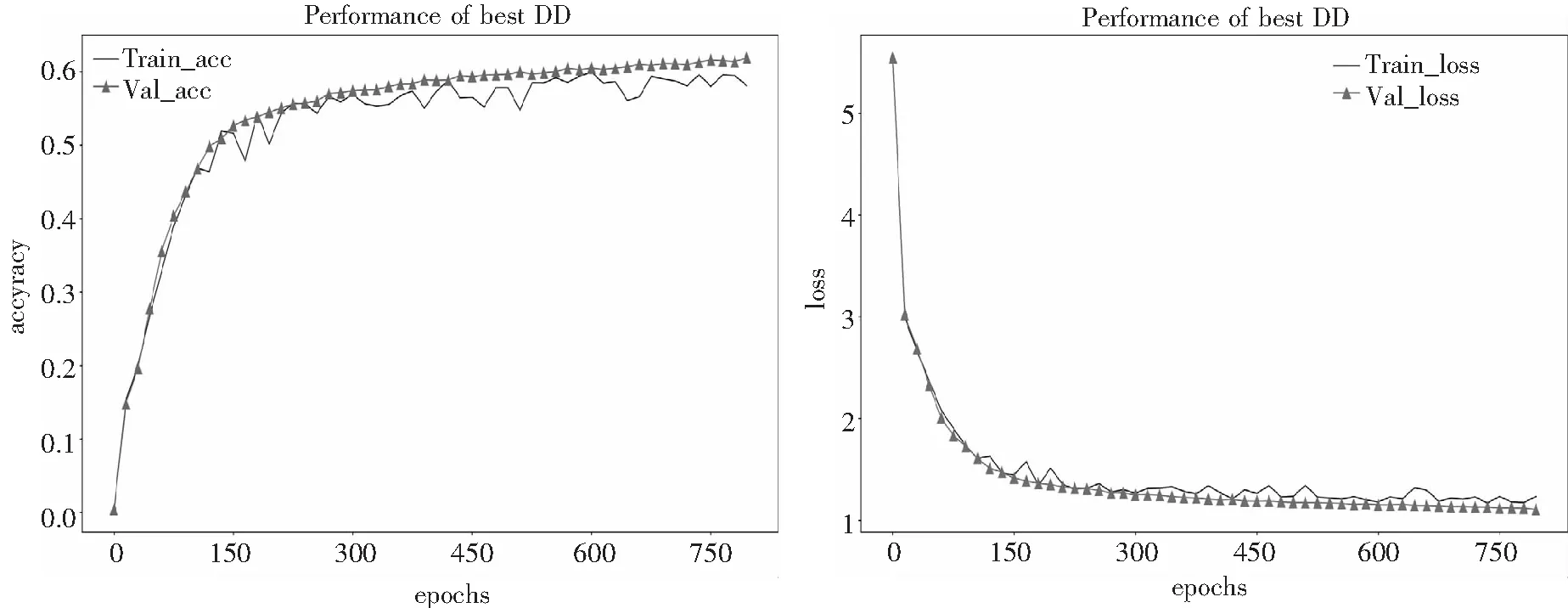
图9 DD模型在加密板A上的表现Fig. 9 The performance of DD model on encryption board A

从实验结果可以看出，在前150个epochs的训练中，DD模型的收敛速度最快，在第150个epochs时，模型在训练集上的准确率提升到了52.67%，loss降低到1.414 9；在验证集上的准确率提升到了51.63%，loss降低到1.450 2.后面随着迭代训练次数的增加，模型的准确率和损失值开始保持平缓的速度收敛，并最终在训练到第800个epochs时，达到最优模型，此时的模型在训练集上的准确率提升到了61.98%，loss降低到1.117 1；在验证集上的准确率提升到了60.31%，loss降低到1.164 4.

3.5 对加密板B的侧信道攻击实验

在对加密板B进行侧信道攻击实验中，DD模型同样是6层结构，其中有三层是DD基础模块结构，神经元数目设置为130个；模型的优化器设置为RMSprop，对应的学习率大小设置为0.001；所有的网络层的use_bias参数均设置为False，即不使用层偏置向量；网络输出层使用softmax激活函数，其余网络层均不设置激活函数.最后整个DD模型一共有100 880个参数，具体的模型结构参数如表2所示.

表2 DD模型结构参数

DD模型分类实验的最终结果如图10所示.从实验结果可以看出，在前50个epochs的训练中，DD模型的收敛速度较快，在第50个epochs时，模型在训练集上的准确率提升到了84.98%，loss降低到0.489 4；在验证集上的准确率提升到了89.17%，loss降低到0.341 5.后面随着迭代训练次数的增加，模型的准确率和损失值开始保持平缓的速度收敛，并最终在训练到第300个epochs时，DD模型达到最优模型，此时的模型在训练集上的准确率提升到了98.86%，loss降低到0.051 8；在验证集上的准确率提升到了98.76%，loss降低到0.052 4.

图10 DD模型在加密板B上的表现Fig. 10 The performance of DD model on encryption board B

最终的实验结果表明，DD模型在加密板A和B上都有很好表现.此外，在加密板A上，DD模型的参数规模有128 400个，模型的验证精度能够达到60.31%；在加密板B上，DD模型的参数规模有100 880个，并且模型的验证精度能够达到98.76%，远高于A板的实验结果，因此，可以发现加密板B比A板更容易实施侧信道攻击，B板的加密安全性更低.

表2(续)

3.6 与几种深度学习模型的对比实验

为了研究DD模型在侧信道攻击中的性能，本文进一步对其余常见的几种深度学习模型进行对比试验.参考文献[2,5]中使用的MLP、CNN和RNN模型结构，对本文的两个数据集，从模型的精度、训练时间、参数规模和侧信道攻击效率等几个方面来综合对比分析所有模型的侧信道攻击性能.

首先针对目标加密板A进行对比实验，实验结果如图11所示.从表3和其右侧的训练时间图可以直接看出，在各模型均迭代训练到第800个epochs时，DD模型的训练总时间最短，分别比MLP 、CNN和RNN模型节省大约7%、25%和92%的时间；DD模型的训练损失略高于RNN模型，但是RNN模型此时有较严重的过拟合现象，而DD模型则是最优模型结构，并且有更高的测试准确率，高达60.69%，比其他模型的结果更好；此外，DD模型的参数规模最小，只有128 400个参数，模型结构最简单，模型的计算复杂度更低.从表4和其右侧的训练时间图可以看出，当各个模型的精度都达到40.00%时，DD模型的训练总时间仍然最短，分别比MLP、CNN和RNN模型节省大约88%、64% 和 94%的时间；DD模型的迭代训练次数最少，仅为74个epochs，模型训练优化速度最快.对比分析结果表明DD模型的优化收敛速度更快，模型精度更高，损失更低，模型参数最少，模型的计算复杂度更低，更容易被训练优化，因此，基于DD模型的侧信道攻击效率更高，综合性能最好.

表3 Epochs=800时各模型的精度和训练时间

表4 Val_acc=0.400 0时各模型的训练次数和时间

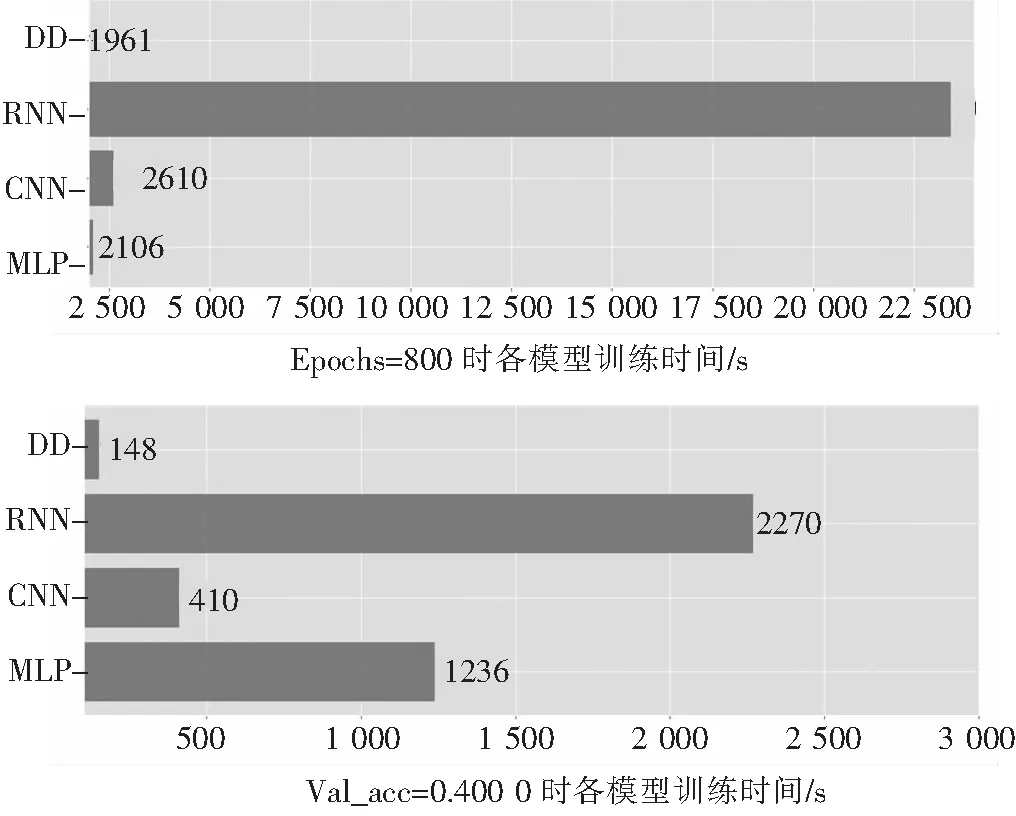
图11 各模型在加密板A上的表现Fig.11 The performance of each model on encryption board A

表5(续)

最后针对目标加密板B进行对比实验，结果如图12所示.从表5和其右侧的训练时间图可以直接看出，在各模型均迭代训练到第300个epochs时，此时的DD模型的训练损失率高于CNN模型，测试准确率达到98.69%，与CNN模型的结果相当，但是DD模型的训练总时间最短，分别比MLP 、CNN和RNN模型节省大约1%、46%和95%的时间；此外，DD模型的参数规模最小，只有100 800个参数，模型结构最简单，计算复杂度更低.从表6和右侧的训练时间图可以看出，当各个模型的精度都达到90.00%时，DD模型的训练总时间仍然最短，分别是MLP、CNN和RNN模型的59%、37%和98%；此时的DD模型迭代训练了70个epochs，略多于CNN模型的结果，但是DD模型训练的时间更短，这进一步证明了DD模型的结构简单，更容易被训练优化.对比分析的结果表明DD模型在收敛速度、模型精度和训练损失方面，与CNN模型相当，但DD模型的训练总时间最短，模型的参数规模最小，模型的计算复杂度最低，因此，基于DD模型的侧信道攻击效率更高，综合性能最好.

表5 Epochs=300时各模型的精度和训练时间

表6 Val_acc=0.900 0时各模型的训练次数和时间

图12 各模型在加密板B上的表现Fig.12 The performance of each model on encryption board B

4 结论

本文提出基于树突网络(Dendrite network, DD)的硬件加密芯片侧信道攻击算法，并通过chipwhisperer实验平台对算法进行测试评价.实验结果表明：(1)在所有的模型中，DD模型的参数规模最小，模型的结构最简单，计算复杂度最低；(2)DD模型的训练时间最短，在加密板A、B上分别只要32分41秒和5分02秒就能收敛到最优模型，远比其他模型收敛速度快；(3)DD模型具有高精度和低损失的优秀性能，在加密板A、B上，最优的DD模型分别能够达到60.69%和98.69%的测试准确率，对应的训练损失分别为1.114 7和0.052 7，与CNN模型具有几乎相同的表现效果；(4)在模型的整个训练过程中，DD模型一直没有出现过拟合现象，并且模型的收敛趋势比较稳定，模型的鲁棒性较高.因此，基于DD模型的侧信道攻击综合性能最优.

实验中可发现在加密板A和B上采集的功耗数据具有高信噪比的特点，这表明数据的噪声小，加密操作的数据信息特征很明显，这也是各个网络模型都能够取得优秀表现的主要原因.但是在实际中，当加密设备在运行加密算法时，会受到各种环境因素的影响，导致研究人员采集到的侧信道数据信噪比较低，数据噪声多.因此，希望在未来的工作中，能够继续去研究深度学习模型在低信噪比数据上的侧信道表现，并寻找出针对低信噪比数据集的侧信道攻击方法，从而提高硬件加密设备的信息安全防护能力.