CFG桩加固软土路基参数敏感性数值分析*

杨川陵，谢晓琴

(1.广州市交通设计研究院有限公司，广东 广州 510030；2.重庆大学 管理科学与房地产学院，重庆 400045)

0 引言

作为交通建设的基础，路基稳定性与变形控制是保障行车安全、高速行驶的基础[1].软土普遍分布于海滨、湖滨等地势较低区域，其中包含较多有机物[2].软土物理性质与淤泥较为相同，具有强度低、压缩量高等特征[3].考虑软土路基的蠕变特征，在软土路基上进行建设时易产生路面流变、隆起与挤出等现象[4].考虑软土路基的各项特性，在修建交通路线时，既要求施工过程中的安全稳定性，又需要保障交通建设完成后的稳定性，同时需要严格把控交通建设后路基沉降.

CFG桩主要应用于软土路基加固应用中，包含CFG桩、褥垫层与基础板等主要结构[5].当前，CFG桩应用过程中不同加筋等技术的应用，使软土路基交通建设设计方案中需要考虑诸多影响因素，如路面动力分析与沉降计算方法等.针对CFG桩加固软土路基，国内外专家进行了较多研究，但研究结果均存在一定差异性，并忽略部分影响因素[6].在沉降计算方法中，当前使用的解析法虽能够获取路基沉降值[7-8]，但针对部分假设条件对沉降值的影响研究较少.基于此，研究CFG桩加固软土路基参数敏感性数值分析方法，并以某公路工程为目标，分析相关参数的敏感性.

1 CFG桩加固软土路基参数敏感性数值分析方法

1.1 工程概况

为实现CFG桩加固软土路基参数敏感性数值分析，本文选择以一处处于剥蚀丘陵间丘间谷区域的公路工程为研究对象，该区域土层分为表层、中层和底层.其中，表层为以砂粒为主的砂质粉土，整体厚度约为14±6 m，岩芯大体表现为散开状；此土层整体呈现浅黄色，多为干燥松软状态，土质相对均匀.中层为以粉粒为主含有大量沙粒的淤泥质粉质黏土，整体厚度约为5.5±3.5 m，土层存在较大空隙，局部存在云母碎片；此土层整体呈现浅黄色，大部分为干燥状态，部分区域存在轻微湿润现象，土质相对均匀.充当持力层的底层为以粉粒为主含铁锰结核的粉质黏土，此土层呈硬塑状态.

工程施工时，将CFG桩部署成正方形，且采用2.9 km长的路基对其进行加固实验处理，同时选取桩径、桩长与桩距的长度分别为0.58 m、10±6 m和1.9±0.1 m.

表1所示为经过现场地质勘查后获取的各土层与CFG桩材料物理力学参数.

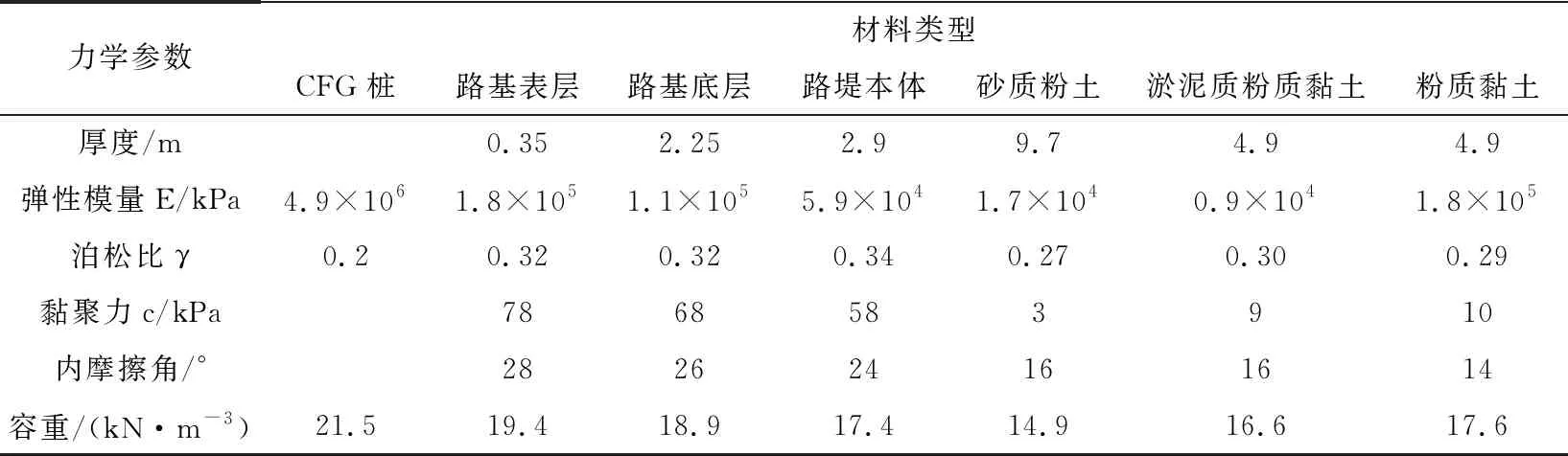
表1 物理力学参数

1.2 数值模拟模型构建

1.2.1 有限元模型基本假定

由平面应变角度出发，将桩墙描述为CFG桩，设置地基宽度与深度分别为60 m和25 m，模拟土体选择四节点实体单元，获取的土体有限元网格如图1所示.

图1 土体有限元网格Fig.1 Soil finite element grid

依据土体弹塑性蠕变线下塑造土体本构模型，土体依据摩尔-库伦准则实现屈服[9-10]，模拟CFG桩、桩帽和路基填土、垫层时运用结构单元以及线弹性模型.路基的填筑模拟流程为：

a.确定自重力条件下地基土的位移与应力；

b.完成垫层与CFG桩施工；

c.路基填筑；

d.设定公路荷载.

路基与垫层物理力学参数如表2 所示.

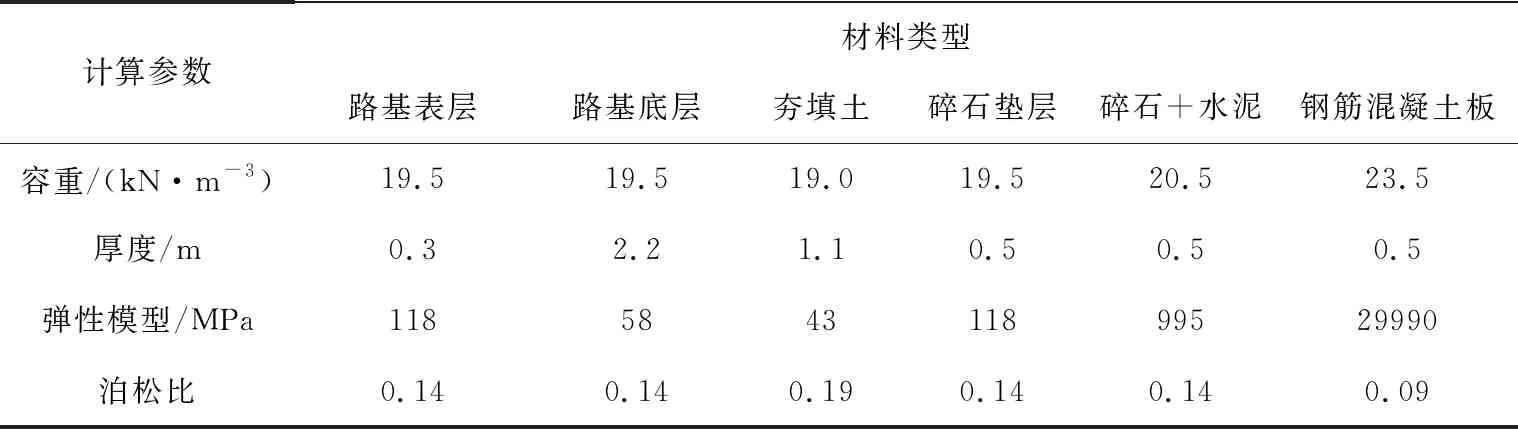
表2 路基与垫层物理力学参数

1.2.2 弹塑性蠕变本构模型

针对土体流变理论，以满足不同需求为目的，本文使用的大量流变模型[11-12]为麦克斯维尔与开尔文串联产生的伯格模型，其流变方程如式(1)所示：

(1)

式中：K和ε分别表示土体黏性和应变；E和η分别表示弹性模型和常量.

受常应力影响的应变为：

(2)

根据式(2)可得，利用时间t的数学函数可描述土体蠕变曲线.

1.2.3 摩尔-库伦破坏准则

在本文构建的模型中，一般可通过剪切破坏条件下，大小主应力描述摩尔-库伦准则，整体应力表达条件下得到：

(3)

式(3)中，ξ和c分别表示内摩擦角和黏聚力.

依据摩尔-库伦破坏准则可得，土体被破坏时，土体平面抗剪强度值将保持稳定.

将摩尔-库伦准则作为黏弹塑性流变模型的屈服条件，实际运算时，蠕变原件获取形成的位移与应力，同时进行迭代.对比迭代过程所获取的结果与莫尔-库伦破坏准则，依照时间进度持续进行迭代过程，至迭代结果平衡为止.通过流变模型描述较为复杂的流变性质[13]，并能够体现软土路基弹性、塑性与黏性特征，且整体呈现软土路基的压缩与剪切等流变特征.

1.2.4 动力荷载时程分析

动力荷载时程分析可划分为两个环节：

(1) 分析有限元模型整体特征值，以此为基础获取模型结构自身动力特征[14]；在时程分析过程内模型阻尼矩阵的运算过程中，采用特征值分析过程中前两个主振型周期；运算过程中，利用地面曲面弹性构建弹性边界.

(2) 在有限元模型内设定黏性边界，以此防止动力分析过程中受波反射影响，导致模型分析误差；将上一环节中获取的前两个主振型周期引入两个模态[15]，限制底部完成后，仿真模型动力响应.

在上述分析过程中，阻尼常数的计算可利用式(4)和式(5)完成，即：利用式(4)和式(5)获取表3中两种阻尼常数.

(4)

(5)

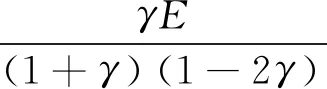
有限元模型内不同材料单位面积阻尼常数的运算结果如表3 所示：

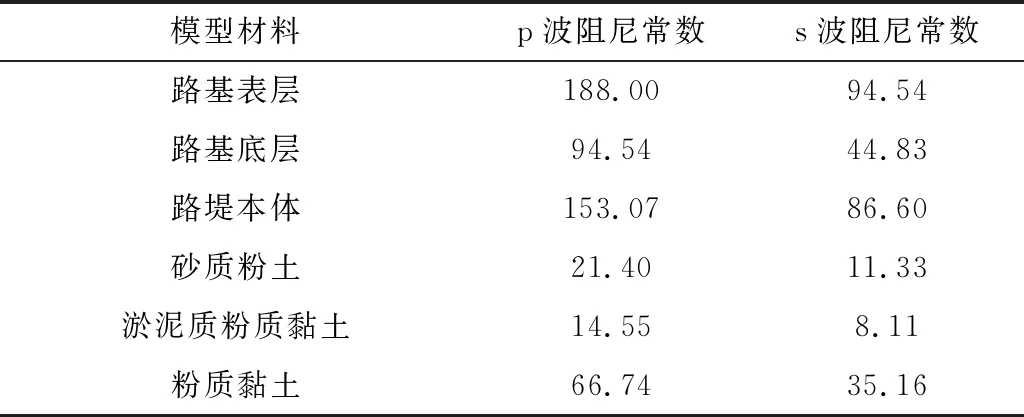
表3 阻尼常数

2 实验分析

2.1 实验方案

采用本文方法所构建的有限元模型，分析所选工程中CFG桩加固软土路基参数敏感性数值.由于分析过程中具有大量工况点，在实际分析过程中，选取其中典型的节点与模型横截面.在工程路基面轴线初始区域、中部区域和终点区域，分别选取一个节点作为分析工况点，具体如图2所示.

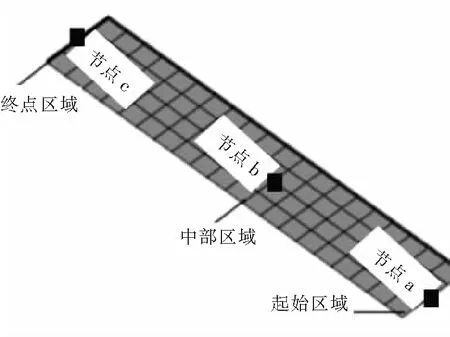
图2 分析工况点Fig.2 Analytical operating conditions

2.2 结果分析

2.2.1 路基面竖向速度依纵向的动力分析

以本文方法所获取的模拟结果为基础，生成的路基面竖向速度波动曲线如图3所示.

对比图3内各图振动速度可知，随着动力荷载的提升，路基上三个分析工况点的振动均产生相应的响应时间.路基面不同区域的竖向速度曲线波动情况具有较为相似的规律，基本表现为正余弦函数曲线波动.

图3(a)中，通过CFG桩加固路基前，节点a在荷载施加的整体过程中，速度波动上限值为19.23 mm·s-1，下限值为-18.45 mm·s-1.相对之下，通过CFG桩加固路基后，速度波动的上限值为14.96 mm·s-1，下限值为-16.74 mm·s-1.由此说明采用CFG桩加固路基后，竖向速度降幅达到22.20%和9.27%.

分析图3(b)得到，节点b通过CFG桩加固路基前后，速度上下限值与节点a和节点c相比均较大.加固前，上限值和下限值分别为28.41 mm·s-1和-27.02 mm·s-1；加固后上限值和下限值分别为25.40 mm·s-1和-24.52 mm·s-1；通过CFG桩加固后，竖向速度降低较多.产生这种状况主要是由于荷载叠加效应提升节点b区域振动效应的显著性，令其振动速度有所提升.基于速度曲线的整体波动趋势分析，节点b区域的竖向速度受CFG桩加固影响并不显著.

分析图3(c)得到，针对节点c通过CFG桩加固路基前，速度上限值为13.31 mm·s-1，下限值为-14.29 mm·s-1；加固后，速度上限值为10.85 mm·s-1，下限值为-12.17 mm·s-1；降幅达到18.48%和14.84%.

图3 路基面竖向速度波动曲线Fig.3 Basic vertical velocity fluctuation curve

综上所述，通过CFG桩加固路基后，路基竖向速度均表现出降低趋势，降低幅度有所差异，并且振动速度下降能够提升路基稳定性.

2.2.2 CFG桩结构对路基沉降影响结果

设定CFG桩结构分别为表4所示的3种基础结构，在表4基础上获取路基沉降不同情况：

表4 CFG桩结构类型

分析图4得到，CFG桩结构刚度与填土荷载下路基沉降之间呈反比例，即CFG桩结构刚度越小，路基沉降越显著.在CFG桩结构为刚性结构的条件下，路基沉降值与CFG桩结构为柔性结构时相比降低45%以上，结果如图4所示.

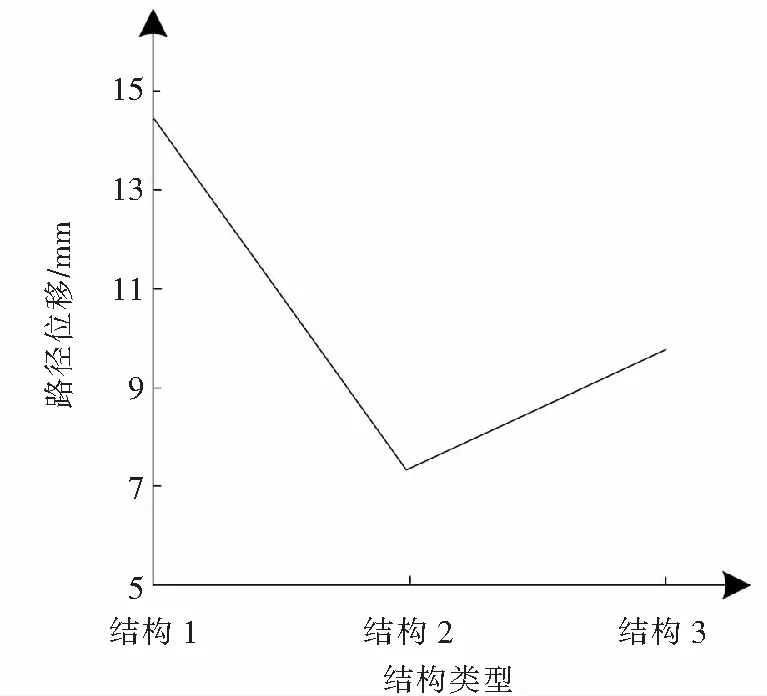
图4 填土荷载影响下路基沉降情况Fig.4 Filling load influence under the road base depth

2.2.3 CFG桩位移随时间变化情况

图5所示为CFG桩位移随时间变化情况，其中实线表示无蠕变条件，虚线表示有蠕变条件.

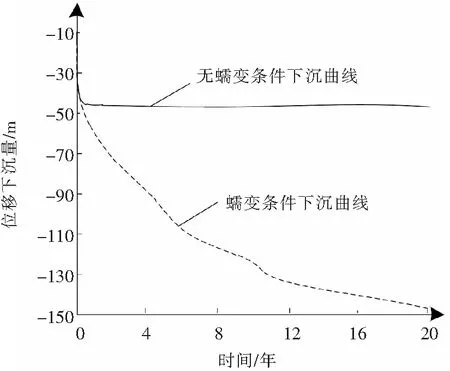
图5 位移随时间变化情况Fig.5 Displacement with time variation

分析图5得到，在路面荷载条件下，路基下沉位移速度有所提升.当无蠕变条件下，路基加固完成后下沉位移大致为-43 mm，在此条件下，路基内部颗粒处于平衡状态，因此在随后的时间中路基停止下沉.有蠕变条件下，路基加固完成后下沉位移大致为-47 mm，在随后的20年中，下沉位移量逐渐提升，达到148 mm.因此，利用GFG桩加固后，考虑蠕变条件下路基的下沉位移持续存在.

3 结论

本文主要分析CFG桩加固软土路基参数敏感性数值，通过本文分析得到，CFG桩软土路基相关参数的敏感性集中表现为：

(1) 路基竖向速度均表现降低趋势，不同区域降低幅度有所差异，路基面轴线中部区域竖向速度上下限值与初始区域和终点区域相比均较大；

(2) CFG桩结构刚度与填土荷载下路基沉降之间呈反比例；

(3) 土体沉降主要为蠕变导致的次固结沉降.