一类具Holling-II功能反应函数的IGP模型的稳定性研究*
秦 晶,张 齐
(1.吉首大学 张家界学院,湖南 张家界 427000;2.中南大学 数学与统计学院,湖南 长沙 410000)
0 引言
自Holt和Polis[1]在1997定义了IGP模型(如图1所示),该模型引起了很多生态学家的重视,该模型证明了共存存在的条件是在共同竞争基础食饵的过程中,IG食饵一定要优于IG捕食者.在此基础上,Tomas Revilla[2]同样对该模型进行研究,得到了除上述结论之外的另一个重要结论:IG捕食者的大小和IG捕食者对IG食饵的作用形式对延伸和限制共存的动力学有重要的影响. 考虑到中间捕食者和高级捕食者的种内竞争,Namba、Tanabe和Maeda[3]提出了新的IGP系统,该文献分析了模型的非负平衡点的稳定性以及所有12个参数作为分支参数的情况,但是遗憾的是在考虑营养级联效应时,却忽视中间捕食者和杂食捕食者的种内竞争系数对其的影响.考虑到功能反应函数,2013年,Kang和Wedekin[4]建立了一类IGP模型,在模型中,IG食饵和IG捕食者对基础食饵的相互作用关系选取Holling-I型功能反应函数,IG食饵和IG捕食者之间的相互作用关系选取Holling-III型功能反应函数,文章给出了两个模型在所有可能的情形下持续生存或消亡的充分条件,并且模型1会出现“top down”现象.2015年,Hsu、Ruan和Yang[5]将经典的IGP系统中所有的功能反应函数均选取为Holling-I型,他们三人用新的视野和观点详细讨论了该模型共存、灭绝、双稳以及周期解和混沌现象出现的条件. 本文在文献[6]的基础上,继续研究模型正平衡点存在的个数和稳定性以及单个物种及多个物种的持续生存和系统的持久性条件,从而丰富其模型的动力学性态.
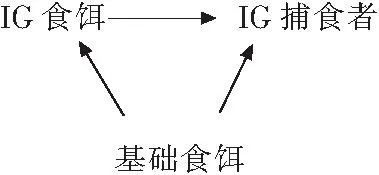
图1 IGP模型图Fig.1 The schematic diagram of intraguild predation model
考虑如下的模型:
(1)
其中:N1,N2,N3分别代表基础食饵,IG食饵,IG捕食者;r1表示基础食饵的内禀增长率;r2,r3分别表示IG食饵、IG捕食者的死亡率;α1为物种的最大增长率;e1代表IG捕食者对IG食饵的转化率;β为半饱和系数;aii为种内竞争系数;aij(i
为了分析方便,采用无量纲化,将系统(1)简化为:
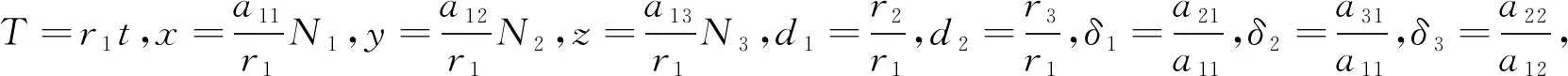
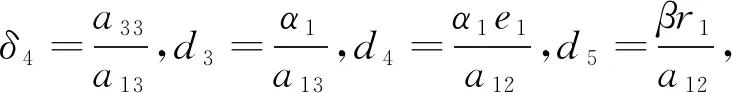
(2)
其中,δi,di>0(i=1,2,3,4),x≥0,y≥0,z≥0.
1 物种的持续生存和系统的持久性
1.1 单个物种的持续生存
命题1x物种总是持续生存的.
证明系统(2)在y-z子系统的ω极限集是A0(0,0,0),且
因此物种x是持续生存的.
1.2 两个物种的持续生存
命题2(i)当δ1>d1且δ2
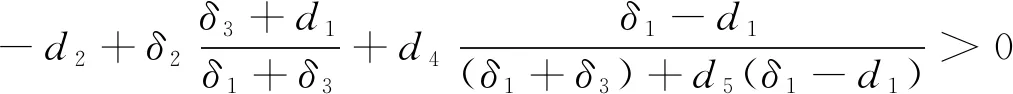
证明由命题1可知,x总是持续生存的,所以x与y的持续生存⟺y物种的持续生存.同理,x与z的持续生存⟺z物种的持续生存.
(i)由前面的证明可知,存在紧集σ=[b,B]×[0,B]×[0,B],使得系统(2)在σ限制在x-z子系统上的ω极限集为:
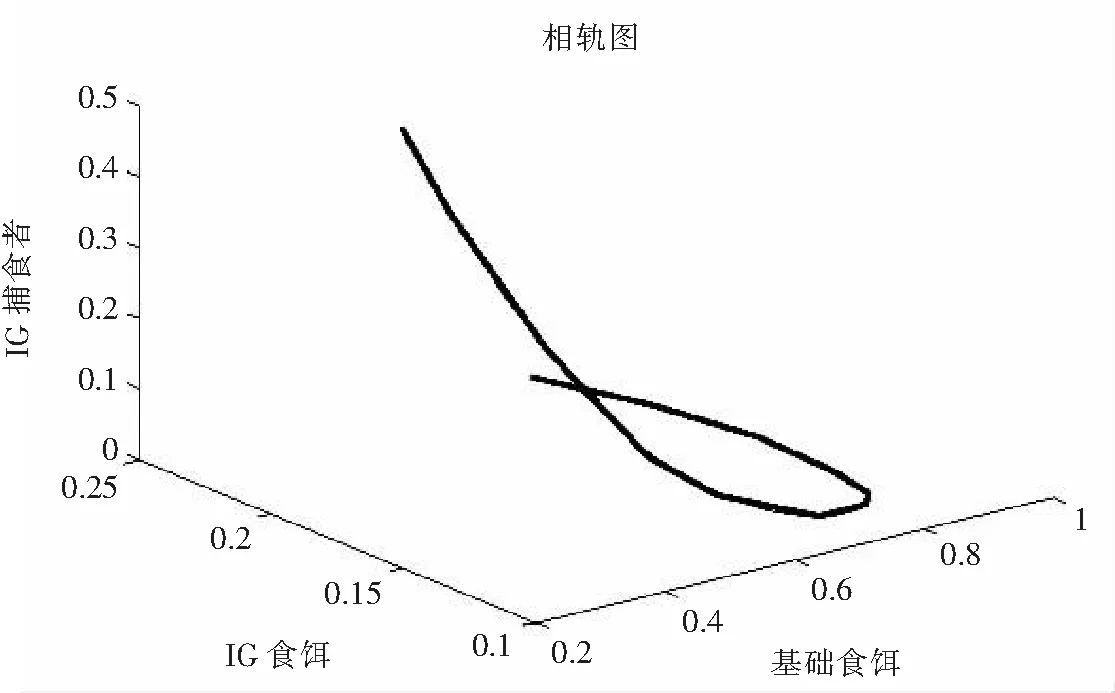
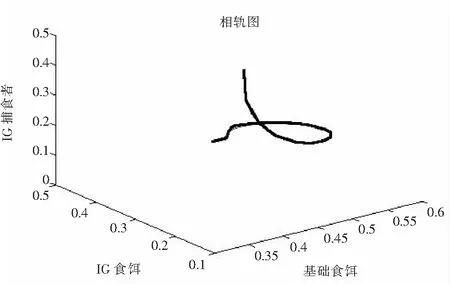
(a)当δ2 当情况为(b),且δ1(δ4+d2)>d1(δ2+δ4)+d3(δ2-d2)时, 因此x,y持续生存的条件为(i). (ii)同理,系统(2)在σ限制在x-y子系统上的ω极限集为: (a)当δ1 所以(ii)的结果成立. 证明系统的持久性要求三物种同时持续生存,综合1.1、1.2节很容易得出命题3. 如果系统(2)存在正的共存平衡点E+=(x*,y*,z*),则一定满足: 1-x*-y*-z*=0, (3) (4) (5) 由式(3)可推出x*=1-y*-z*,代入式(4)得: (6) 将x*=1-y*-z*代入式(5)得: (7) 由式(6)和(7)可推出 令 f1=(δ1-d1)-(δ1+δ3)y, 由f2=0可知 (8) 整理式(8)得 δ2d5y2+[(δ2-d4)-d5(δ2-d2)]y-δ2+d2=0. (9) 设式(9)的两根为y1,y2,由根与系数的关系可知: 由此可知f2=0只有一个正实根,设为y0. 当f1(0)>f2(0)时,即δ1(d2+δ4)>d1(δ2+δ4)+d3(δ2-d2),有图(a)、(b)、(c)、(d)四种可能的情况;当f1(0) 所以系统有可能出现0,1,2,3个内部平衡点(如图2所示),使得它们共存. 图2 正平衡点可能的个数Fig.2 Possible numbers of interior equilibria 设正平衡点E+=(x*,y*,z*)的雅可比矩阵为 (10) 其中: A11=1-2x*-y*-z*,A12=A13=-x*,A21=δ1y*, 它的特征方程为: 即 λ3+aλ2+bλ+c=0. 其中: a=-(A11+A22+A33), b=A11(A22+A33)+A22A33-A23A32-A12A21-A13A31, c=A11(A23A32-A22A33)+A12(A21A33-A23A31)+A13(A31A22-A21A32). 我们可以得到如下的定理: 定理1 当满足下列条件时: i)M<0; ii)D<0; iii)D1+D2+D3>0; iv)M(D1+D2+D3)-D<0, 正平衡点E+=(x*,y*,z*)渐近稳定. 证明由上面的假设可知a=-M,b=D1+D2+D3,c=-D,ab-c=D-M(D1+D2+D3),由条件i)、ii)、iii)可知a>0,b>0,c>0,而λ3+aλ2+bλ+c=0的Routh判定表为 利用Matlab软件,选取符合命题3(a)的条件对系统(2)的持久性进行数值模拟,得到图3,图3的参数分别为d1=0.5,d2=2.4,d3=d5=1,d4=5,δ1=δ3=δ4=1,δ2=2,x(0)=0.4,y(0)=0.2,z(0)=0.5,从图中可以清楚地看到,当满足命题3(a)条件时,系统是持久的. 图3 满足命题3(a)的x,y,z的三维相轨图Fig.3 3D-phase plane of x,y,z satisfying 3(a) 同样选取满足命题3(b)的条件,得到图4,图4的参数分别为 图4 满足命题3(b)的x,y,z的三维相轨图Fig.4 3D-phase plane of x,y,z satisfying 3(b) d1=d2=0.5,d3=0.8,d4=0.2,d5=0.6,δ1=2,δ2=δ3=δ4=1,x(0)=0.4,y(0)=0.2,z(0)=0.5.由图可知,此时系统是持久的. 将第1部分的结论还原成原始系统即系统(1),可得到如表1所示的持续生存结果. 表1 系统(1)的持续生存结果 本文研究了一类具有密度制约且带Holling-II功能反应函数的IGP模型,利用ω-极限集理论得到了单个及多个物种持续生存和系统持久性的条件,同时采用Routh-Hurwitz判定定理及渐近稳定定理分析了系统正平衡点存在的可能个数及渐近稳定性,最后将简化后的系统还原成原始系统,得出原始系统物种持续生存的条件,同时采用Matlab软件对系统的持久性进行数值模拟,验证了结果的正确性.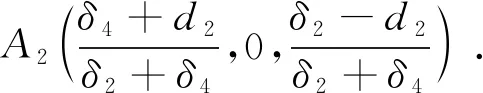
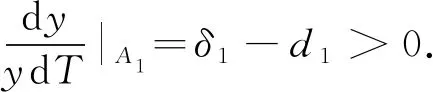
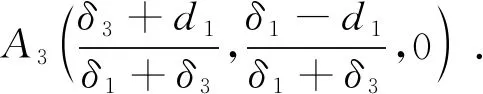
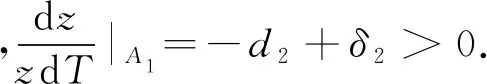
1.3 系统(2)的持久性(三物种的持续生存)
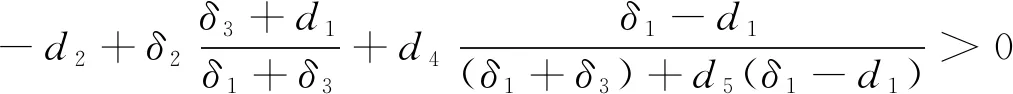
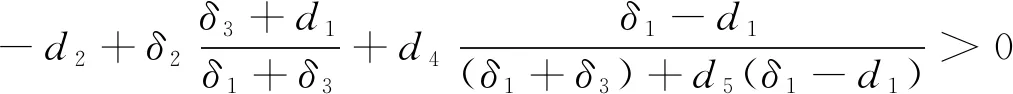
2 正平衡点存在的个数和稳定性
2.1 正平衡点存在的可能个数

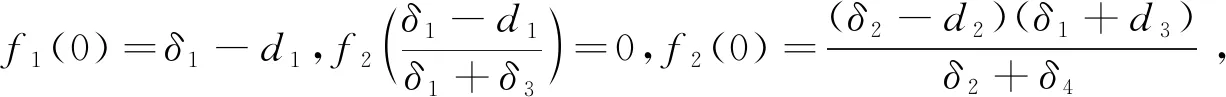
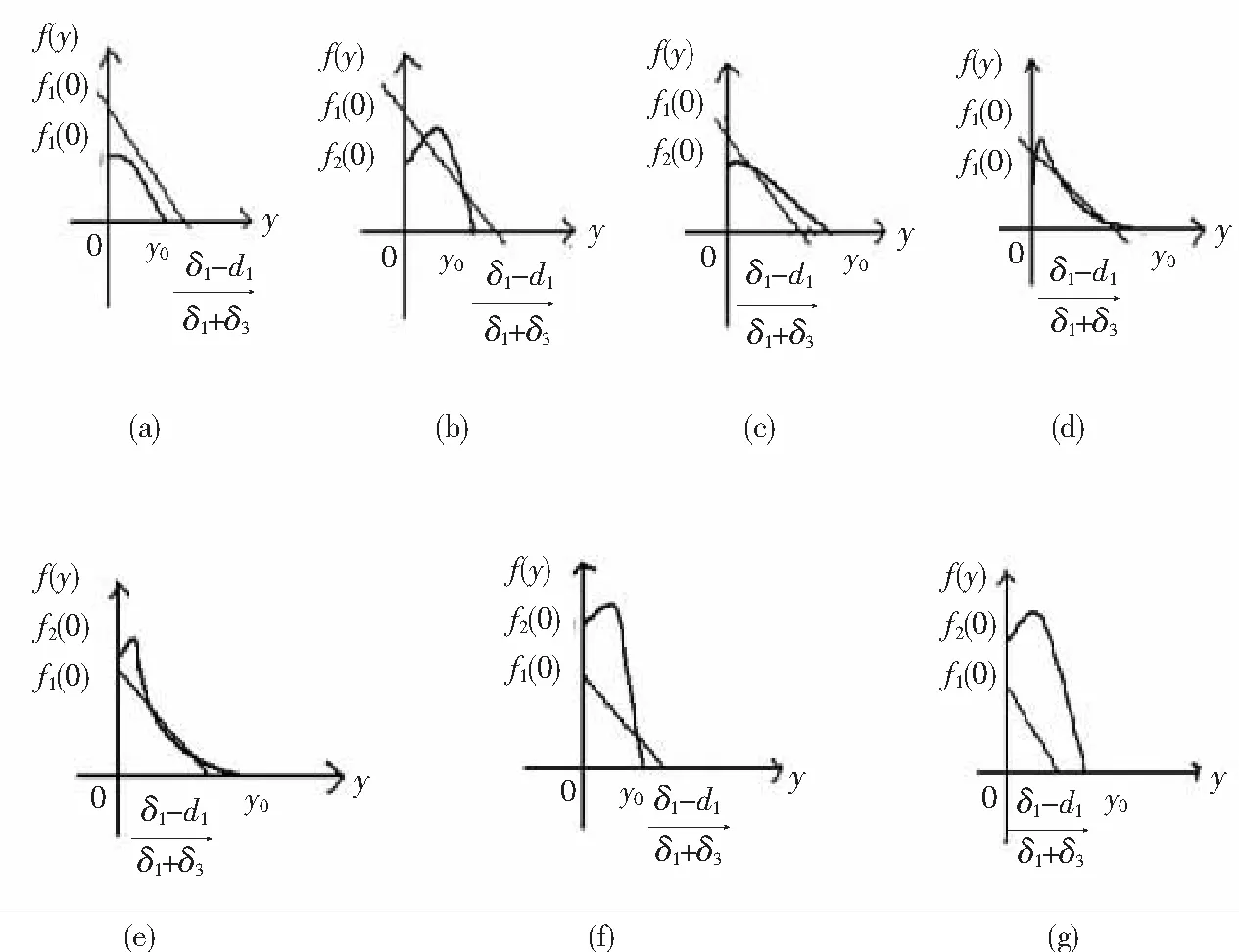
2.2 正平衡点的稳定性
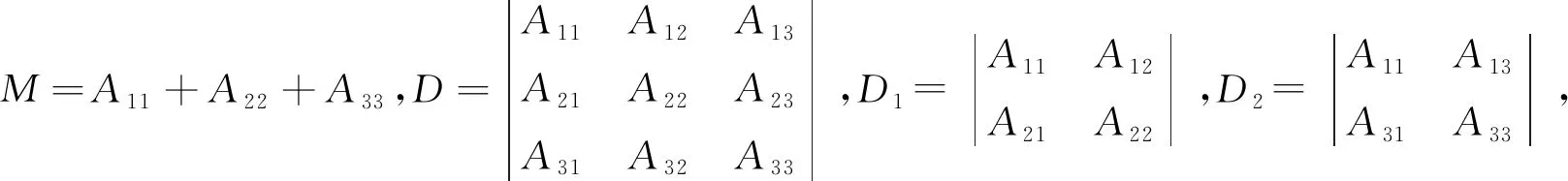
3 系统(2)的持久性数值模拟
4 系统(1)的物种持续生存结果

5 总结

