基于全参数化建模的高速客船型线优化设计

谢玲玲，张守慧，冯佰威，田中文

(1.武汉理工大学 高性能船舶技术教育部重点实验室，湖北 武汉 430063；2.中国船级社 海南分社，海南 海口 570206；3.中船黄埔文冲船舶有限公司，广东 广州510715)

0 引 言

船体型线设计是船舶整体设计非常复杂和重要的部分，船舶的结构设计、性能计算、机舱布置和生产放样均基于船体型线。通常，基于一些基本规则和相关设计经验，针对船舶特性，确定1个或多个船体型线设计方案，通过多次模型测试改进型线并最终确定。船体型线设计通常需要手动修改，效率较低。因此，如何快速生成船体型线是船舶设计需要解决的重要问题。

基于计算流体动力学(Computational Fluid Dynamics，CFD)数值模拟方法，通过CFD数值计算寻找最佳设计方案[1-5]，该方法不仅可快速找出最佳方法，而且可更节省大量的人力、时间和试验成本。

1 船体型线全参数化建模

采用CAESES FRIENDSHIP-Framework软件进行全参数化建模。首先，通过分析船体型线特征，构建控制主要特征的参数化曲线；然后，根据建立的特征曲线，采用剖线生成器生成光顺的横剖线；最后，通过曲面生成器模块Meta Surface，依据生成的剖线，采用蒙面法生成光顺的船体曲面。图1为某型高速客船全参数化模型。

图1 某型高速客船全参数化模型

2 阻力性能数值计算

SHIPFLOW是与CEASES参数化建模软件相结合、进行船体参数化优化应用较多的一个软件。许多研究表明，SHIPFLOW软件中的势流计算和黏流计算模块可有效求解船体阻力性能，因此选取该软件进行水动力性能计算。

2.1 计算区域

采用SHIPFLOW软件进行船体阻力预报，其计算区域如图2所示。水流方向必须是由船体艏部至艉部。区域1为势流计算区域，采用Rankine源法，按照线性和非线性的自由表面边界条件进行高阶面元法的势流理论计算，后续的兴波阻力计算主要在该区域进行。区域2为薄边界层区域，根据边界层理论求出边界层厚度，对该区域船体边界层进行计算可得到船体前部2/3的摩擦阻力[6]。区域3为黏流计算区域，包括船体后部、船体下游和整个流域尾部，采用纳维-斯托克斯方程(Navier-Stokes Equations，N-S方程)、k-ε湍流模型和壁面函数进行求解。

图2 计算区域示例

2.2 CFD计算

2.2.1 计算模型

船模具体参数如表1所示。

表1 船模参数

2.2.2 网格划分

网格划分影响后续阻力优化是否成功。SHIPFLOW软件自带网格划分功能，在XMESH中进行势流计算的面元网格划分，在XGRID中进行黏流结构化体网格划分。经多次设置计算，确定在进行黏流计算时采用该软件的fine网格模式，在进行势流计算时采用该软件的medium网格模式。船体曲面面元网格如图3所示。船体势流计算网格与计算区域如图4所示。

图3 船体曲面面元网格

图4 船体势流计算网格与计算区域

2.2.3 数值分析

船体阻力系数CT的计算公式为

CT=CV+CW=CF+CPV+CW=

(1+h)CF+CW

(1)

式中：CV为黏性阻力系数；CW为采用压力积分法进行计算得到的兴波阻力系数；CF为摩擦阻力系数；CPV为黏压阻力系数；h为形状因子。

SHIPFLOW软件对兴波阻力进行计算的方法为横切波法和压力积分法，横切波法对网格质量的敏感性相对较低。对初始模型进行阻力性能计算，分析计算结果发现：采用压力积分法得到的初始模型兴波阻力数值较船模高很多，而采用横切波法则与船模接近。因此，确定后续计算采用横切波法。船模与初始模型的15 kn(低速)、17 kn(中速)和19 kn(高速)(简称“多航速”)兴波阻力数值如表2所示。由表2可知：船模与初始模型的兴波阻力数值在多航速下误差均在1%内。因此，初始模型可保证船型在阻力性能方面的拟合度和后续船型优化中的计算精度。

表2 多航速兴波阻力数值

3 特征参数灵敏度分析

采用Sobol算法对选取的13个船体艏部特征参数进行灵敏度计算。在蒙特卡洛方法中，Sobol算法属于拟蒙特卡洛方法，其优点在于是一种样本分布均匀、稳定、覆盖率很好的序列[7]。蒙特卡洛方法关键在于随机数的生成，目前发展较快的是数学方法。Sobol算法基于半随机的Sobol序列，其生成原理是基于1个以2为底数的不可约多项式生成多个方向数，对每个选定的优化变量由确定性计算生成伪随机序列，设计方案以一种标准形式在整个空间域内进行传播，使变量在设计空间内均匀分布。传统的无约束优化算法在进行全局优化中具有一定的缺陷，而用Sobol算法在规定的研究空间内对最优解优化方向进行初步探索，所求的解不一定是最优解，但可以其作为研究对象，选择其他优化算法进行进一步优化，从而节省优化时间。经灵敏度分析，得到灵敏特征参数及其最佳取值范围，如表3所示。

表3 灵敏特征参数及其最佳取值范围

4 多航速船体型线优化

4.1 设计变量

将表3中的8个灵敏特征参数的变量上下限数值作为优化模型的设计变量。

4.2 约束条件

在模型优化过程中，将湿表面积和排水体积作为约束条件，使优化后的湿表面积和排水体积较优化前的误差保证在±1%内，其约束公式为

(2)

(3)

式(2)和式(3)中：Sopti为优化模型湿表面积；Sorig为初始模型湿表面积；▽opti为优化模型排水体积；▽orig为初始模型排水体积。

4.3 优化目标

将15 ℃无风无浪海水中的多航速兴波阻力作为优化目标并求其最小化。

4.4 优化结果数值分析

多航速优化模型的船体艏部特征参数数值如表4所示。多航速优化模型的约束条件和优化目标数值变化如表5所示。优化后的湿表面积和排水体积均满足误差绝对值在1%内，且兴波阻力在多航速下均有所降低。

表4 多航速优化模型的船体艏部特征参数数值

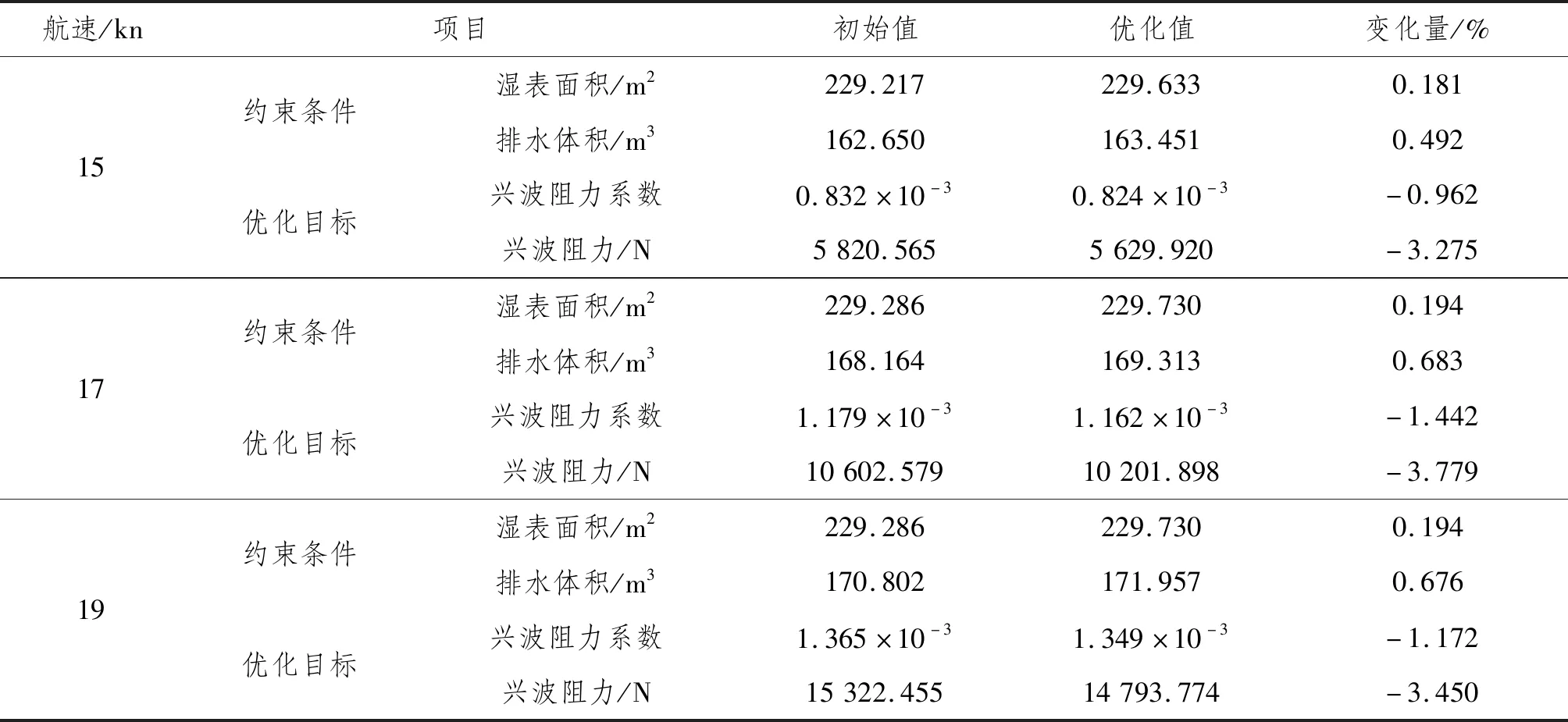
表5 多航速优化模型的约束条件和优化目标数值变化

4.5 优化结果图形分析

优化模型的效果主要根据由波浪引起的自由液面波形图及船体表面的压力系数分布图进行分析比较。

优化模型与初始模型的多航速自由液面波形图对比如图5所示。由图5可知：在15 kn航速下，优化模型的最大波幅较初始模型有所降低，波数也有所降低，且幅值也较小；在17 kn和19 kn航速下，优化模型的波幅较初始模型无太大变化，波切图波形走势大体相同，但优化模型的波切图波幅较初始模型有所减少。

图5 多航速自由液面波形图对比

优化模型与初始模型的多航速船体表面压力系数分布如图6所示。由于只对船体艏部型线进行优化，因此在优化后，船体艉部表面压力系数分布无大的变化。由图6可知：优化模型的船体艏部压力在多航速下较初始模型均明显缩小，随着压力系数的减少，兴波阻力也相应降低。在优化方案中，船体艏部压力梯度在多航速下均变缓，且优化模型的船体前部压力分布向船体后部移动，这样优化后的兴波分离降低，从而兴波阻力也相应降低。

图6 多航速船体表面压力系数分布

对多航速优化模型与初始模型的型线进行对比，如图7和图8所示。由于只对船体艏部型线进行优化，因此船体艉部型线并无变化。由图7和图8可知：优化模型的船体艏部型线具有急速收缩的趋势，水线面面积减少，从而导致兴波阻力系数减少。

图7 船体艏部横剖线对比

图8 船体艏部型线俯视图对比

5 结 语

对多个优化方案进行分析，通过多次比较流场和阻力，优化模型在多航速下均具有良好的流场分布和较缓的压力梯度分布，其兴波阻力在多航速下较初始模型均明显降低，且水面兴波也较小。对于优化后的型线，除船体艏部具有1处存在稍不平缓现象外，其他各处均满足曲线和曲面光顺性的要求，由于在船舶建造过程中可进行人工光顺，因此这种情况对兴波阻力影响很小。综合分析，可认为对某型高速客船的船体阻力性能优化是成功的。