乌江航道千吨级船舶K、T指数计算方法

谢凤云， 金 雁

(武汉理工大学 交通学院，湖北 武汉 430063)

0 引 言

随着“长江经济带”的提出与逐步推进，长江航道对于加强沿海与沿江内陆之间人员往来、货物运输的功能愈发凸显。郑德高等[1]认为长江经济带未来可发展成为一种新的空间结构，并以此带动长江复合交通走廊的建设。作为长江上游南岸最大支流的乌江，是国家规划的内河高等级航道的重要组成部分[2]，其沿线货物运输需求快速增长。据估计，现有乌江航道的通过能力将很快趋于饱和。由于现有乌江航道船舶基本是500 t以下的小型船舶，因此需要开发适应于乌江航道的千吨级标准船型。

良好的船舶操纵性对于船舶综合性能至关重要。船舶K、T指数是评价船舶航向稳定性和回转性的重要指标，合理评价船舶K、T指数在船舶设计的初始阶段具有重要意义。K、T指数的计算方法由日本学者野本谦作提出，野本法通过Z形操舵试验计算K、T指数。船舶K、T指数通常由实船试验测得。为较快获得K、T指数，基于回归分析方法的经验公式和基于计算流体动力学(Computational Fluid Dynamics，CFD)的计算方法成为补充方法。刘晨飞等[3]基于船舶操纵运动数学模型研讨小组(Ship Maneuvering Mathematical Model Group,MMG)模型建立KVLCC2船模的操纵运动模型，利用龙格-库塔方法求解微分方程组，对船舶进行操纵仿真。洪碧光等[4]基于31艘商船的实船试验结果，利用多元线性回归的方法，考虑对船舶K、T指数影响较为显著的变量，得到这些无量纲化参数对K、T指数的影响，并给出计算K、T指数的经验公式。姚杰等[5]基于11条渔船的K、T指数资料，选取3个对K、T指数影响较显著的因素，采用多元线性回归方法进行统计分析，给出计算中小型渔船K、T指数的经验公式。李宗波等[6]利用SPSS软件对43艘商船K、T指数资料进行回归分析，提出2个最优回归公式并利用1条杂货船进行验证，计算结果较为符合实际情况。张显库等[7]利用SPSS软件对59条商船的K、T指数统计资料进行分析，考虑数据间的非线性影响，构造四元二阶多项式回归模型，通过在数据库中增加渔船等中小型船舶，扩大回归公式的普遍性。蔡创等[8]采用浅水修正的MMG船舶操纵运动方程，研究浅水条件对船舶回转性和航向稳定性的影响并基于浅水修正的MMG船舶操纵运动模型计算K、T指数的准确性。张彬[9]提出一种简单的船舶K、T指数计算方法，结合地球经纬度，简化船舶操纵运动控制方程的求解过程。李小冬等[10]选取6个船舶设计变量为计算目标：采用最优拉丁超立方设计方法选取28个设计方案，基于CFD方法和经验公式计算船舶水动力导数，通过求解Abkowitz方程对船舶进行回转模拟仿真并得到战术回转直径；采用回归分析法，研究计算参数对船舶战术回转直径的灵敏度，结果表明对船舶战术回转直径影响最大的计算参数是船宽吃水比和船长船宽比。

虽然现在有很多计算K、T指数的经验公式，但是这些经验公式有的只针对一种船型，对于其他船型并不适用；有的经验公式虽然涵盖船型较多，吨位涉及范围较广，然而样本库中缺乏千吨级样本，对于乌江航道千吨级船舶也不适用。乌江航道千吨级标准船型受限于乌江航道水流湍急、河床狭窄等特点，以及沿江船闸、桥梁对船舶主尺度的制约，其船舶主尺度和船舶型线与其他内河船舶及乌江航道原有船舶有较大区别，需要按照新设计标准船型构建新的K、T指数计算经验公式。

1 理论模型

船舶操纵运动数学模型有以Abkowitz方程为代表的整体型模型和以MMG方程为代表的分离型模型。整体型模型综合考虑船、桨、舵的相互作用，直接求解船舶整体运动方程；分离型模型利用水动力导数描述船、桨、舵之间的相互作用，分别求解作用在船、桨、舵上的作用力。以无限水深MMG方程为船舶操纵运动控制方程，考虑浅水修正，得到乌江千吨级船舶操纵运动控制方程。

1.1 船舶操纵运动数学模型

考虑到乌江航道风浪较小，船舶运动相对平稳，因此在船舶操纵运动方程中仅考虑纵荡、横荡和艏摇等3种船舶运动姿态。船舶三自由度运动方程为

(1)

考虑分离型MMG模型，将作用在船舶上的力分离为作用在船体、螺旋桨和舵上面的力，在进行无量纲化后，得到无量纲化MMG船舶操纵运动控制方程为

(2)

式中：右上角标为船舶参数的无量纲化；下标中的H0为裸船体、P为螺旋桨、R为舵、C为流、s为岸壁作用。

作用在船体上的流体作用力可分为惯性流体力和黏性流体力。其中：惯性流体力可根据元良诚三图谱进行估算；黏性流体力在小漂角时按照贵岛模型估算，在大漂角时按照芳村模型估算，当漂角处于大、小漂角之间时利用插值法估算黏性流体力。

螺旋桨伴流系数可按照汉克歇尔回归公式计算，其计算式为

wP0=0.7Cpa-0.30

(3)

式中：Cpa为棱形系数。

Cpa的计算式[11]为

(4)

式中：Fr为船舶弗劳德数。

螺旋桨推力系数可按照三叶系列桨的推力系数试验图谱，考虑盘面比影响所给出的回归公式。

螺旋桨推力减额系数亦可按照汉克歇尔回归公式计算，其计算式为

tP0=0.5Cpa-0.18

(5)

考虑乌江水系的复杂水流特性，需要计及流的作用对船舶运动的影响，可将非均匀流等价为均匀流进行计算。

1.2 MMG模型验证

为验证第1.1节所述计算模型的准确性，将从某型散货船的船模试验得到的Z形操舵试验结果与基于MMG模型得到的模拟仿真结果进行对比，船模尺度要素如表1所示。

表1 船模尺度要素

图1为船模操纵试验实况。Z形操舵试验曲线如图2所示。由图2可知：实船试验结果与模拟仿真结果差别较小，说明所采用的MMG模型能很好地模拟实船Z形操舵试验的结果。但是有一些数据，比如第一超越角和第二超越角，在仿真值与试验值之间尚有较大的相对误差，说明在计算水体对船舶的流体作用力时偏小，导致艏向角计算过大，从而过高估计船舶的回转性。

图1 船模操纵试验

图2 Z形操纵曲线对比图

2 经验公式回归

2.1 系列船舶仿真

依照现有乌江航道千吨级船舶的主尺度、螺旋桨要素和舵要素，选取一系列船舶样本库。将这些样本的船、桨、舵的相关要素代入所构建的MMG方程中，可得到每条船的无因次化K、T指数。将计算得到的样本K、T指数结果与一些相似船型实船试验测得的无因次化K、T指数的结果[12]进行对比，可发现这些计算所得到的K、T指数处在合理区间内。图3为编号为1～4的4条试验船在Z形操舵试验中舵角和艏向角随时间的变化曲线。

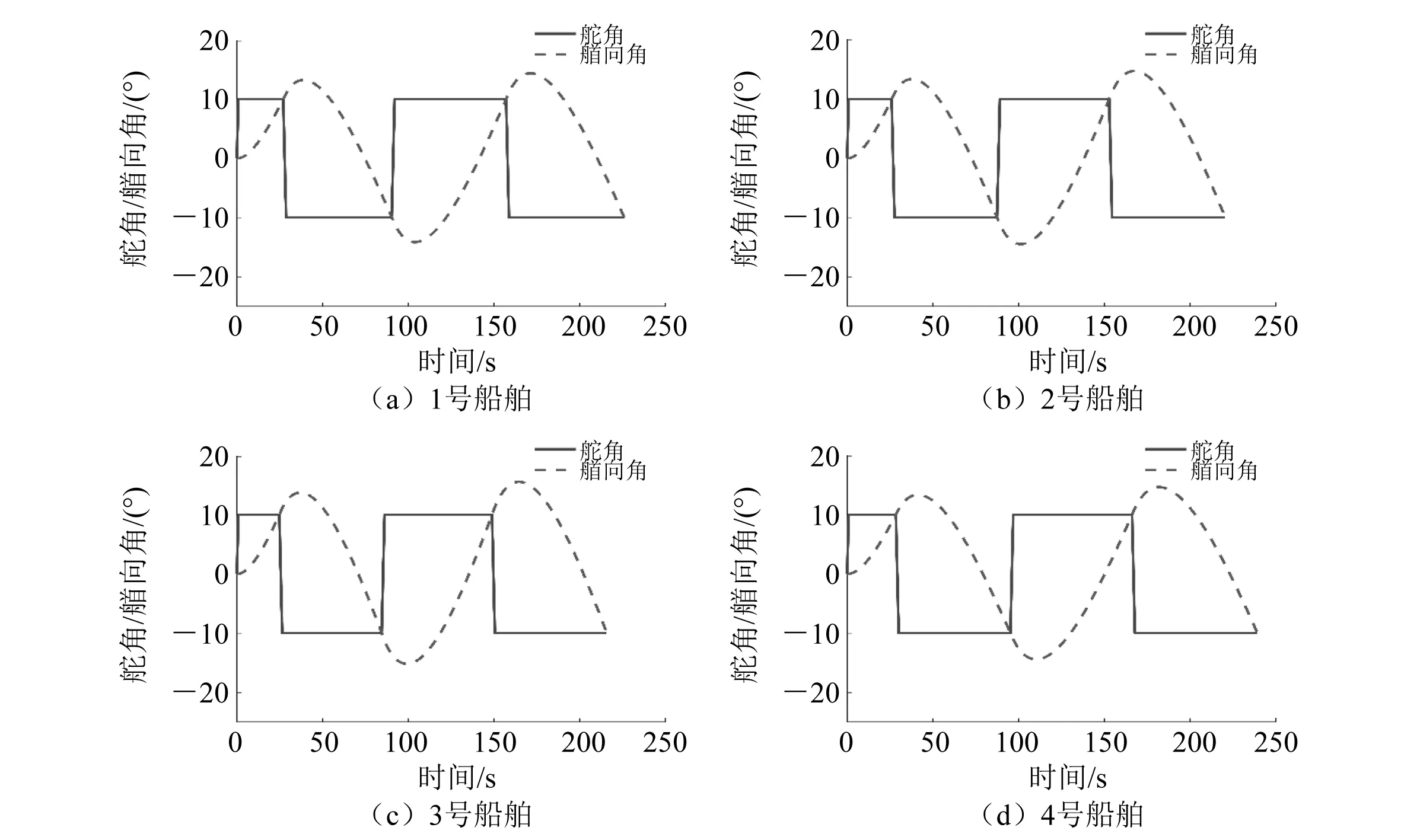
图3 部分样本船舶Z形操舵曲线

2.2 K、T指数计算经验公式

由于样本库的数据较少，无法选择过多的参数进行经验公式回归，如文献[3]选取5个无量纲化参数，是由于其样本数据较多。在文献[3]中样本船舶吨位一般较大，且船型较多，针对乌江航道千吨级船舶不一定适用，针对性不够。此外，一般研究认为船舶Fr对K、T指数的计算有一定影响，如文献[2]选取船舶Fr作为一个无量纲参数加入经验公式中，且认为Fr越大，船舶旋回性越好。考虑乌江航道千吨级船舶属于宽浅吃水船型，呈现宽扁、肥大的特点，且船长Fr一般较小，因此不考虑Fr在经验公式计算时对船舶K、T指数的影响。基于一般经验公式的选取方案，考虑对船舶K、T指数影响最为显著的因素，选择方形系数Cb、船长船宽比L/B(L为船长，B为船宽)和船舶水下侧面积与舵面积之比Ld/AR(Ld为船舶水下侧面积，AR为舵面积)等3个参数作为经验公式中的无量纲自变量。

在第2.1节中所选取的系列主尺度船舶样本的无量纲参数和计算所得的无因次化K、T指数(即K′、T′)如表2所示。

表2 系列船舶无量纲参数和无因次K、T指数

为更准确地表示所选参数对船舶K、T指数的影响，在经验公式中采用交叉二次回归方式。交叉二次回归充分考虑自变量之间的相互影响。基于MATLAB程序编制回归K、T指数计算经验公式的脚本。利用MATLAB内嵌的交叉二次回归方法可较容易地获得所给数据库的回归公式。将表2中的数据输入脚本中后，可得到回归公式中的各项系数和公式的残差。根据MATLAB的计算结果，得到基于所选3个无量纲化参数计算K、T指数的回归公式，分别如式(6)和式(7)所示。

无因次化K指数的计算经验公式为

(6)

无因次化T指数的计算经验公式为

(7)

计算所得到的残差如表3所示。由表3可知：计算得到的残差比较小，说明所得到的回归公式在该样本中有较高的精确度。

表3 经验公式计算残差 10-12

3 经验公式验证

为验证所得到的经验公式的准确性，将现有的3条船的实船尺度要素和实船试验资料与式(6)和式(7)的计算结果进行对比。3条实船的无量纲参数，实船无因次化K、T指数和经验公式回归得到的无因次化K、T指数如表4所示。

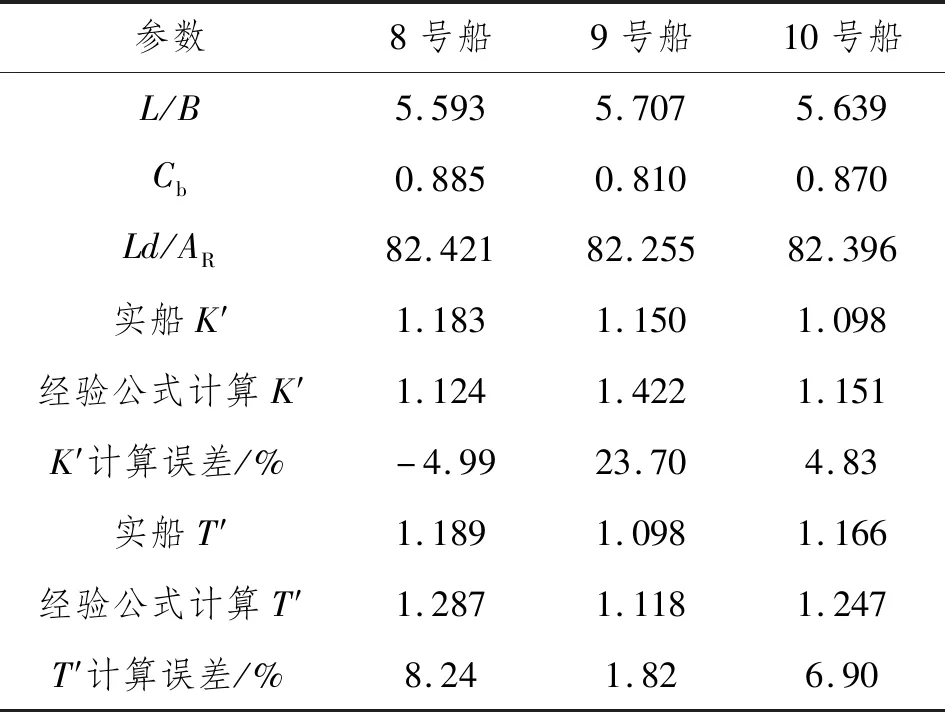
表4 实船试验数据与经验公式计算结果对比

由表4可知：8号和10号船的方形系数与样本较为接近，而9号船则偏离稍远。对于另外2个无量纲化参数，这3条船与船舶样本都较为接近。无因次化K指数的误差分别为-4.99%、23.70%、4.83%；无量纲化T指数的误差分别为8.24%、1.82%、6.90%。经验公式计算所得到的结果与实船结果较为吻合。除9号船的无因次化K指数相差较大外，其他指数的误差都控制在10%内，说明经验公式有较高的准确度。此外，所得到的参数基本大于试验值，说明利用所得到的2个经验公式计算无因次化K、T指数有过高估计的趋势。

4 结 论

基于MMG分离型模型求解船舶操纵运动方程，通过与船舶试验资料的对比验证模型的准确性。在此基础上利用MMG模型得到系列船舶的Z形操纵运动曲线，基于野本法求得无因次化K、T指数，从而得到关于方形系数Cb、船长船宽比L/B和船舶水下侧面积与舵面积之比Ld/AR等3个无量纲参数的计算无因次化K、T指数经验公式。得到如下结论：

(1)所选取的系列船舶K、T指数的计算结果表明该船型的综合操纵性能优良，适应于乌江航道。

(2)对经验公式影响较大的因素是船舶的方形系数Cb和水下侧面积与舵面积之比Ld/AR，但这只是定性分析，需要更加细致地分析参数对计算结果和参数之间的相互影响，还应进行敏感性分析。

(3)用经验公式计算得到的无因次化K、T指数与实船数据吻合较好，但是在计算2号船的无因次化K指数时，出现较大的误差，这是由于2号船的方形系数严重偏离船舶样本中方形系数。因此，为提高所得经验公式的准确性，还应计算范围更大、数量更多的样本。