基于带置信区间稳定图的铁路连续梁桥模态参数识别

王秋萍 秦世强

武汉理工大学土木工程与建筑学院，武汉430070

高速铁路桥梁运营过程中，列车和桥梁形成一个车桥耦合系统，系统的动力响应十分复杂，会影响行车安全。为评价车桥耦合动力学行为，准确识别结构的模态参数十分重要［1-2］。模态参数包括频率、阻尼比和模态振型，是结构基本的动力参数，也是进行结构动力分析、损伤识别的基本参数。与传统测力法相比，环境激励的模态参数识别方法通过测试结构在风、水流、地脉动等环境荷载下的微幅振动响应，结合时域、频域算法识别结构模态参数，具有测试简便、无须额外激励设备，不会对结构造成损伤等优点。因此，环境激励的模态参数识别方法在桥梁工程领域得到广泛关注和应用［3-4］。

随机子空间识别（Stochastic Subspace Identification，SSI）是一种时域识别方法，是环境激励模态参数识别中较为可靠的一种算法。西宁北川河桥［5］、岸桥［6］、Millau高架桥［7］等已经验证了SSI算法的实用性。基于环境激励下的结构动力响应，通过SSI算法识别结构模态参数分为四个步骤：①数据采集；②数据预处理；③系统矩阵识别；④模态参数识别。第4步也称作模态分析后处理，主要是利用稳定图方法来确定各个测试组数据识别的频率和阻尼比，并整合各个测试组的信息识别模态振型。对于分多个测试组完成的桥梁环境振动测试，这种后处理十分繁琐，不仅要处理多个测试组的数据，而且须要区分稳定图中虚假模态，使得整个模态分析过程效率大幅降低。

许多学者针对这个问题开展了研究。樊江玲等［8］在稳定图中引入了一种可表征各阶模态贡献量的分量能量指标作为稳定判据，从而剔除虚假模态。陈永高等［9］引入余弦相似定理，提出频率相似度和振型相似度，从而剔除稳定图中虚假模态。Reynders等［10］提出模态转移范数ni的概念来区分系统真实模态和虚假模态，ni越小，该阶模态是虚假模态的可能性就越高。常军等［11］提出一种两阶段稳定图的方法，首先对输出信号进行分段构造稳定图，然后对各段识别的模态参数再一次用稳定图方法分析，从而去除虚假模态。Cara等［12］通过研究各阶模态对实测响应的贡献，确定了系统阶次的选定方法，避免系统阶次过高带来虚假模态或过低引起模态遗漏。

在上述研究基础上，针对稳定图中存在的系统阶次确定较为随意和虚假模态问题，本文提出基于奇异熵增量的系统阶次计算方法和带置信区间的稳定图，并通过一座高速铁路连续梁桥对带置信区间稳定图的效果进行验证。

1 随机子空间识别

结构的随机状态空间模型为

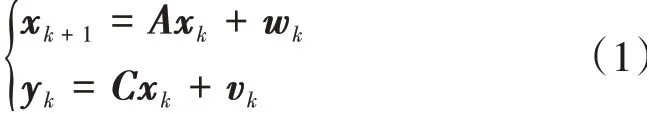
式中：x k、x k+1分别为系统在第k、k+1个时间点处的状态向量；y k为测试到的输出响应向量；w k、v k分别为测试过程误差和系统建模误差，均假定为互不相关的白噪声；A、C分别为系统的状态矩阵和输出矩阵。

随机子空间识别的主要思路是通过实测输出响应向量y k识别系统矩阵（AC），结构的模态参数可通过系统矩阵特征值分解获取。有两种方式识别系统矩阵：①直接从响应数据出发构建Hankel矩阵，引入卡尔曼滤波、正交投影和QR分解，称为数据驱动的SSI（SSI-data）；②从响应数据的协方差出发构建输出协方差矩阵（Toeplitz矩阵），引入奇异值分解，称为协方差驱动的SSI（SSI-cov）。两种方式得到的结果近似，但计算效率不同；另外，SSI-cov识别过程更容易量化模态参数的方差［13］。因此，本文选择SSI-cov作为试验模态分析算法。SSI算法较成熟，不再赘述其理论过程。详细的SSI算法实现过程可以参考文献［6］。

2 系统阶次的确定

系统阶次n是SSI算法中须要确定的一个参数。由于模态以共轭对形式出现，因此系统阶次取偶数。系统阶次取值过小会导致结构真实模态遗漏，而取值过大会出现虚假模态。因此，合理地估计系统阶次十分重要。

确定系统阶次的方法主要有两种：

1）奇异值分解法。通过观察Toeplitz矩阵奇异值分解（Singular Value Decomposition，SVD）的结果来确定系统阶次。当系统阶次逐渐增大时，奇异值会逐渐减小至0。这种方法在数值模拟中比较精确，但实际工程中Toeplitz矩阵的奇异值并不是突变到0，而是缓缓地减小，通过观察奇异值的变化很难确定系统阶次。

2）稳定图法。基本思路是给系统阶次赋予一个较大的值nmax，循环求解每个系统阶次对应的模态参数，然后以频率为横轴、系统阶次为纵轴绘制稳定图，稳定图中的散点称为稳定点，须满足相邻两阶频率的相对误差dfi不超过1%、相邻两阶阻尼比的相对误差dξi不超过5%，相邻两阶模态振型的模态置信准则（Modal Assurance Criterion，MAC）值的相对误差dMACi不超过1%。结构真实模态的稳定点会逐渐形成一条稳定轴，而虚假模态一般只会形成一些离散点。

目前，稳定图方法已经成为SSI算法的通用工具，其有效性已经在许多工程实例中得到证明。合理地确定稳定图中nmax具有一定的价值。当nmax取值较大时，循环求解各阶模态参数的计算时间会显著增加，且虚假模态会逐渐形成稳定轴，影响系统模态的拾取。本文在已有研究的基础上，提出一种奇异熵增量加权法来估计系统阶次。

熵是反映系统不确定度的一个指标。对奇异值而言，奇异熵Ek定义为

式中：k为奇异熵的阶次；ΔEi为奇异熵阶次i时的奇异熵增量，可以通过下式得到。

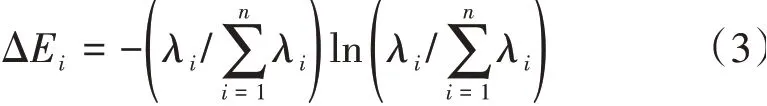
式中：λi为Toeplitz矩阵的奇异值。

奇异熵增量在低阶时λi较大，在高阶时λi较小，且λi随系统阶次的增加逐渐减小，这种变化规律不随信号的噪声情况而改变。已有研究利用奇异熵增量的一阶导数来判定系统阶次，当奇异熵增量的一阶导数趋于稳定时，对应的阶次即为系统阶次。然而，这种方法仍须要作图观察。本文利用奇异熵增量的特性构造奇异熵阶次i处的权重系数εi。εi定义为

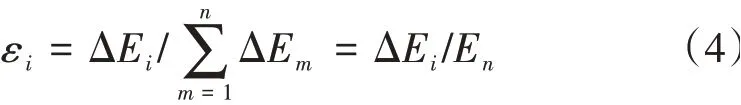
计算得到系统阶次n，即

系统阶次n应取其邻近的较大偶数。该方法简单易行，避免了作图观察，且便于模态参数自动化识别。

3 带置信区间的稳定图

稳定图方法中另一个问题是虚假模态。引起虚假模态的原因包括实测过程产生的信号噪声以及计算假定带来的模拟误差。信号噪声引起的虚假模态可以通过信号预处理、合理选定系统阶次避免，而模拟误差则须要量化。量化的误差称为模态参数的不确定度σ，能够衡量模态参数的可信程度。在SSI算法中，模态参数最终从状态矩阵A和输出矩阵C获得。因此，模态参数的不确定度由A和C的误差导致，即识别的A和C仅仅是其真实值的估计

为了分析系统状态的变化，首先分析可观矩阵O i的一阶扰动ΔO i， 即

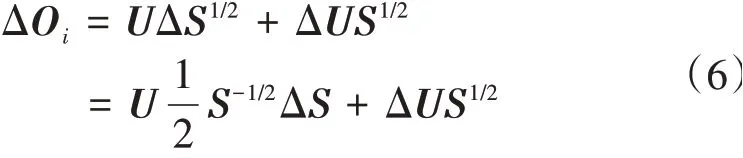
式中：U、S分别为输出协方差矩阵奇异值分解后得到的正交矩阵和对角矩阵；ΔU、ΔS分别为正交矩阵和对角矩阵的一阶扰动。

由于状态矩阵A可以写成可观矩阵O i的表达式，因此，状态矩阵A的一阶扰动ΔA可以表达为

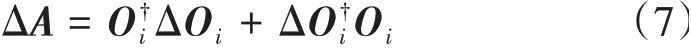
式中：（·）†表示（·）的广义逆。

此时，问题转化为如何求解正交矩阵和对角矩阵的一阶扰动ΔU和ΔS。具体步骤：基于矩阵敏感性分析推导状态矩阵的一阶扰动，并量化单个测试组识别的模态参数的不确定度；构建频率置信区间（f±σf）和阻尼比置信区间（ξ±σξ），σf、σξ分别为频率f和阻尼比ξ的不确定度，并将其以误差图的形式绘制于稳定图中，用于辅助判断虚假模态。置信区间越大，表明模态参数的不确定度越高，是虚假模态的可能性就越大；反之，表明是结构真实模态的可能性越大。

4 连续梁桥模态参数识别

4.1 桥梁概况

Jalon高架桥位于西班牙境内，是一座高速铁路连续梁桥，主桥跨径布置为（35+45×4+35）m。主桥全长250 m，采用单箱单室等高截面双线梁，箱梁顶宽12.94 m，底宽5.90 m，截面高3.22 m，见图1。

图1 桥梁立面及横截面

4.2 环境振动试验

为研究该桥的动力特性，须对其进行环境振动测试。设置12个GeoSIG无线加速度传感器，其中4个作为参考点传感器，其余8个作为移动测点传感器。每个测试组采样时间约为15 min，采样频率为200 Hz；测点均布置于箱梁内部，每个截面共布置3个测点（参见图1），沿桥纵向每隔2.5 m设置1个测试截面，共101个测试截面，303个测点，见图2。

图2 测点布置及参考点位置（单位：m）

测试组4中参考点27处横向加速度响应见图3。可知，在环境激励作用下桥梁呈微幅振动状态，最大横向加速度未超过1×10-3m/s2。

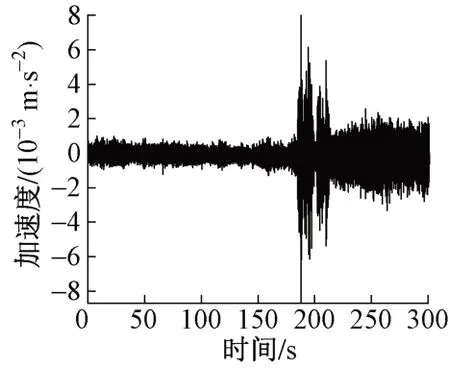
图3 参考点27处横向加速度响应

4.3 识别结果分析

利用测试组4中加速度数据构建输出协方差矩阵得到奇异值分解结果和对应的奇异熵增量，见图4。可知：奇异值随系统阶次变化无明显突变，很难通过观察奇异值变化情况来确定系统阶次；随着系统阶次的增加，奇异熵增量逐渐减小。按照前文方法计算得到系统阶次为49.3，将系统阶次设置为50时即可得到结构的低阶模态。

图4 奇异值与奇异熵增量随系统阶次变化曲线

通过分析测试组4的数据得到带置信区间的稳定图，见图5。图中频率误差线显示了各个稳定点的准确程度，尤其频率为0～1 Hz时，存在较多不确定度较高的稳定点，影响了系统模态的拾取。当频率不确定度σf≤0.25、阻尼比不确定度σξ≤0.25时，图5（a）中的虚假模态和离散点会被剔除，得到图5（b）所示的稳定图，其更利于人工拾取真实模态。此外，图5（a）中频率为4～6 Hz时稳定轴发生了分裂，另一个稳定轴频率不确定度相对较高，须进一步判定是否为结构真实模态。通过引入置信区间，能够较好地区分部分虚假模态和真实模态，有效提高拾取稳定轴的效率。

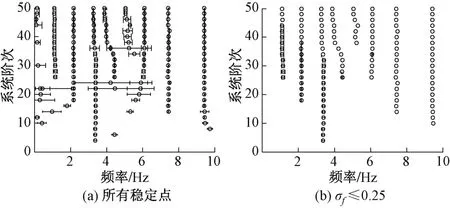
图5 带置信区间的稳定图

按照上述方法对其余测试组的数据进行处理，并获取与图5（b）类似的带置信区间稳定图进行各测试组模态参数的融合，以获得模态参数的试验值。为了校核试验值，采用ANSYS建立桥梁有限元模型，通过理论模态分析获取模态频率的有限元计算值。采用实体单元模拟混凝土箱梁，采用梁单元模拟桥墩；边界条件按图纸设置，在E-1处设置移动铰支座，在E-2处设置固定支座；桥墩底部采用固结处理。

桥梁模态参数识别结果见表1，其中频率和阻尼比的试验值为各测试组识别结果的均值。

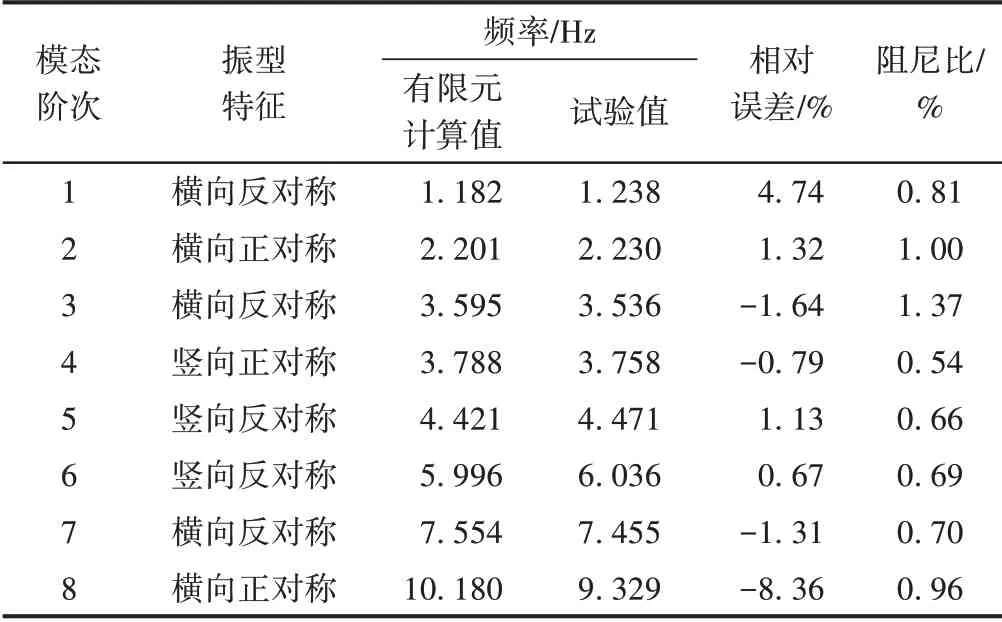
表1 桥梁模态参数识别结果

由表1可知：①频率试验值与有限元计算值吻合良好，横向振动模态中，第1、2阶频率有限元计算值略低于试验值，第3、7、8阶频率有限元计算值略高于试验值；②除第8阶外，其余阶次频率有限元计算值和试验值的相对误差未超过5.00%；③第8阶频率有限元计算值与试验值相对误差为8.36%，相对低阶模态较高，但未超过10.00%；④由于环境激励对桥梁的激励程度有限，高阶模态的识别误差相对低阶模态较高。竖向模态频率的试验值与有限元计算值基本一致。⑤最大阻尼比不超过1.37%，阻尼较低。

5 结论

1）基于奇异熵增量的系统阶次计算方法简单易行，避免通过观察奇异值的变化情况来确定系统阶次，且能够在程序编制中直接实现，利于模态识别过程自动化。

2）带置信区间的稳定图能够有效区分系统真实模态和虚假模态。由于信号受实测过程误差等因素影响，对有些虚假模态须进一步判定，但带置信区间的稳定图仍能去除部分虚假模态。改进的稳定图方法能够有效协助用户进行模态参数识别后处理，提高SSI算法后处理的效率。

3）带置信区间的稳定图识别出的桥梁模态参数试验值与有限元计算值吻合良好，表明带置信区间的稳定图能有效应用于工程结构模态参数识别。