基于离散伴随的流场反演在湍流模拟中的应用

闫重阳，张宇飞，陈海昕

清华大学 航天航空学院，北京 100086

精确模拟湍流流动是许多工程应用和学术研究问题的关键。由于较低的计算成本和较高的稳健性，在工业界的CFD仿真领域，雷诺平均(Reynolds Averaged Navier-Stokes, RANS)模型将在可见的未来继续占有重要地位[1]。然而，传统的RANS模型是针对简单、经典的流动而校准的，在许多实际的场景下缺少足够的仿真能力，例如翼型分离流、强逆压梯度流，或者具有高流线曲率的流动[1]。为了弥补传统RANS模型在某些流动场景下的不足，人们曾提出过多种改进。例如，非线性涡黏模型放弃了雷诺应力张量与应变率张量成线性关系的假设；雷诺应力模型则放弃涡黏假设，直接对雷诺应力建立输运方程。然而，这些更为复杂的RANS模型在计算准确度提高的同时，产生的代价是计算稳定性下降、计算成本升高。另外，如何校准这些复杂RANS模型所带来的诸多新的参数也是对湍流建模者的一个挑战。

作为一种有别于传统湍流建模思路的方法，数据驱动的湍流建模近年来正在逐渐兴起。这一变化得益于数十年来计算资源的大幅增长，用于湍流模型校准的实验数据与DNS(Direct Numerical Simulation)数据的增加，以及采样、统计推断、机器学习方法在湍流建模中的应用。从数据驱动的湍流建模角度来看，湍流模型方程的模化过程，包括雷诺应力的计算、模型方程源项的建立、方程系数的选取等等，都会引入不确定性，这种不确定性通过RANS方程的前向传播，最终会产生CFD预测结果的不确定性。数据驱动则意味着使用统计方法来量化或减少湍流模型的不确定度[2]。围绕这个问题，根据不同的应用目的，可以将主要的研究方向分为3类。

第1类研究是RANS模型不确定度量化(UQ，又称前向方法，无数据方法)。这类研究旨在确定模型不确定性对QoI(Quantity of Interest)分布的影响。当给定湍流模型中不确定性参数的变化范围或先验概率分布时，通过不确定度量化，可以得到QoI的变化范围或概率分布。此类研究通常使用蒙特卡罗方法。例如，Platteeuw等针对零压力梯度平板流动，使用概率分配法(PCM)研究k-ε模型系数的不确定性影响[3]；Dunn等针对后台阶流动，使用拉丁超立方采样方法研究了k-ε模型系数对再附点、摩擦系数等的影响[4]。

除了模型系数以外，不确定性还可能来源于模型方程形式(例如方程源项)或者模化项本身(例如涡黏性ν，雷诺应力τ)。Emory等针对平面槽道流、方腔二次流和跨声速凸块流动，进行了基于雷诺应力不确定性的UQ分析：通过将雷诺应力推向满足可实现性约束的极限情况，来向模型注入雷诺应力不确定性，从而得到QoI的分布范围[5]。

第2类研究被称为后向方法，即根据可观测数据推断模型不确定性参数的后验分布。假设模型不确定性参数为θ，θ的先验分布已知，此类研究的目的是在给定实验或DNS观测数据G的情况下，计算出θ的后验分布p(θ|G)。这本质上是一个贝叶斯推断问题：

p(θ|G)∝p(G│θ)p(θ)

(1)

第3类研究则引入机器学习方法以进行模型改进[13-14]。作为一种研究思路，Parish和Duraisamy提出了FIML(Field Inversion and Machine Learning)用于数据驱动建模的范式[15]：首先通过流场反演得到空间分布的修正场，然后利用机器学习建立修正值与当地流动特征的映射，最后把该机器学习模型加入到RANS模型中，在每一步迭代中动态给出修正量的值，这样就得到了增强的RANS模型。Parish和Duraisamy[15]将FIML成功地应用于一个一维传热问题和k-ω模型计算的一维槽道流。Singh等也利用神经网络建立了当地流动特征到β(x)的映射，从而得到了能够更准确预测翼型分离流动的增强版SA模型[16]。Duraisamy等则分别针对SA模型绕凸壁边界层流动、k-ω-γ三方程模型平板边界层旁路转捩问题应用了FIML[17]。

本文使用基于离散伴随的流场反演，对2个典型的湍流分离问题进行了研究，即结冰翼型绕流和周期山分离流。利用有限的实验数据，对SA模型输运方程生成项的乘子进行贝叶斯推断，以达到对流场及湍流模型的修正。在本文中，针对周期山的流场反演可被归结为一个约束优化问题，而常规的伴随方法在解决约束优化问题上较为低效。本文发展了约束增广的伴随方法，从而使其处理周期山流场反演问题的效率大大提高。计算结果表明，基于伴随优化的流场反演能以相当高的精度拟合指定的实验数据。进一步的分析展示了流场反演作为一种数据驱动方法的意义：一方面通过对湍流模型不确定参数的贝叶斯推断，把有限的实验数据中的信息泛化到整个流场，从而使修正后的整个流场在一定程度上更接近真实流场；另一方面给出了具有明确物理意义的修正量分布，可以直接作为下一步的机器学习增强模型的学习目标，也可为人工湍流建模提供重要参考。

1 流场反演框架

1.1 流场反演问题构建

Spalart和Allmaras构造的经典SA一方程湍流模型中的标量输运方程为[18]

(2)

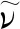
(3)

P为生成项，D为破坏项，其具体形式为

(4)

(5)

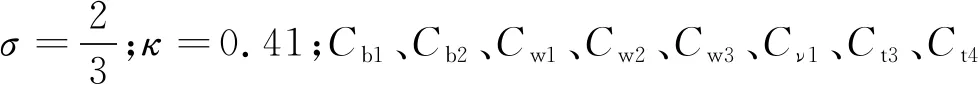
(6)

式中：β为空间坐标x的函数。从数据驱动湍流建模的角度而言，β(x)是一个空间上的随机场，遵循一定的概率分布。在获得实验数据或DNS数据之前，可以为β人为指定一个先验分布p(β)，它代表了研究者对湍流建模的先验知识[19]。在得到实验数据或DNS数据d之后，可以根据贝叶斯定理推断得到β的后验分布。其中d可以是积分量，例如升力系数；也可以是空间或物体表面某些位置的流场数据，例如表面摩擦系数Cf分布等。

在本文中，无需求出β(x)完整的后验概率分布函数，只需对β(x)进行最大后验推断即可。该优化问题可以用梯度优化算法结合离散伴随进行求解。把所有空间点上的β值组装为一个向量β，β是一个随机向量。同理，所有空间点上的观测值组成了观测值向量d。假设β的先验p(β)、观测值d都服从高斯分布，则求解β的最大后验值变为如下的优化问题：

(β-βprior)TCβ-1(β-βprior)]

(7)

式中：h(β)为模型在特定β取值下所预测的QoI；βprior为β先验分布的均值；Cm、Cβ为观测值d以及修正量β先验分布的协方差矩阵。式(7)右边实际上为p(β|d)的对数，其中第1项代表了模型预测的QoI与实验值之间的偏差，第2项代表了β与其先验均值之间的偏差。

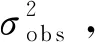
(8)

(9)

式中：1为所有分量都为1的向量。此时的目标函数可以写为

(10)

σobs和σβ的相对大小决定了观测值和先验对β后验影响的权重。至此，对于SA模型的流场反演问题归结为以β为设计变量，以式(10)为目标函数的优化问题。

1.2 离散伴随方法

伴随方法是一种可以高效求解目标函数对设计变量梯度的方法，常结合梯度类优化算法用于解决优化问题。从Pironneau[20]、Jameson[21]开始，伴随方法广泛被用于飞机的气动优化设计。伴随方法的优势在于其计算量与设计变量的个数无关，因此特别适合于设计变量是全场分布的参数场的流场反演问题。

早期的气动优化设计所使用的伴随方法被称为连续伴随。在该方法中，需要首先推导伴随方程，并施加适当的边界条件；然后将伴随方程离散化并迭代求解[22]。然而，连续伴随在方程推导(特别是黏性项、边界条件的处理)、代码实现上较为复杂，限制了它在工程上的应用[23]。随后，Elliott和Peraire[24], Nielsen和Anderson[25]发展了离散伴随方法，首先将Navier-Stokes方程和目标函数离散化，然后在此基础上直接构造离散形式的伴随方程。相比连续伴随，离散伴随的计算速度更快，梯度求解的精度更高，并且大大减少了代码开发的时间[22]。

气动目标函数J、RANS方程的残差R可以写为空间网格坐标x、空间流场变量w的函数：J(w,x)，R(w,x)。离散伴随的求解目的是在所有网格点上RANS方程的残差R(w,x)=0的约束下，得到目标函数J(w,x)对设计变量x的全导数：

(11)

对R(w,x)取微分，得：

(12)

故

(13)

引入伴随变量φ，满足：

(14)

则

(15)

1.3 约束增广伴随方法

一些流场优化问题具有特定的气动约束，例如翼型/机翼定升力系数优化，内流道问题的定质量流量优化等等。对于每个气动约束，往往有一个增广设计变量(如攻角、体积力等)，通过调整该增广设计变量来满足该气动约束。

作为一种解决方法，可以用梯度优化算法(如SQP、SNOPT)处理约束优化问题。对于每一个气动约束，可以把它直接作为优化算法的约束，同时增加一个对应的增广设计变量。伴随算法则需要分别给出目标函数和约束对原始及增广设计变量的导数。然而，由于增广设计变量的存在，设计空间过大，其中的大部分区域都是不满足气动约束的，因此优化效率较低。如果离散伴随能直接提供目标函数在满足气动约束下对设计变量的全导数，那么就只需处理原始设计变量，可以大大提高约束优化的效率。

(16)

式中：

式(16)展开为

(17)

步骤2逐行求出中间矩阵M。对每一个约束RC,i：

(18)

步骤3求增广流场变量的伴随φC:

(19)

步骤4求原始流场变量的伴随φ：

(20)

(21)

相比普通伴随方法，约束增广伴随方法只需针对每个气动约束再求解一次伴随方程，所增加的计算量与普通伴随相当。由此可以大大提高气动约束下的伴随优化效率。

2 结果验证

2.1 结冰翼型绕流算例

2.1.1 算例介绍

结冰翼型的失速预测是飞机安全性十分关注的一个问题。在大攻角下，结冰翼型在位于前缘的冰型上会发生流动分离，并在后方形成较大的分离泡。现有的SA模型对于这样的分离流动不能准确预测。本文选取加盖了角状冰型944的GLC305翼型作为研究对象，对其在特定攻角下的流场进行了流场反演。该冰型的实验数据由NASA格伦研究中心获得，并被作为本文流场反演的观测数据[28]。

GLC305_944结冰翼型的计算网格如图1所示。流向和法向分别有457和97个网格点，同时在冰型附近的加速区也做了一定网格加密。为保证壁面y+<1，壁面第1层网格的高度小于1×106c(c为弦长)。计算的来流条件为：来流马赫数Ma∞=0.12,雷诺数Re=3.5×106，攻角α=6°。

图1 GLC305_944结冰翼型的计算网格Fig.1 Computation grid for iced airfoil GLC305_944

原始SA模型在该工况下计算出的升力系数CL=0.49, 而实验CL=0.67。图2展示了原始SA模型的流场分布图，其中速度u是在ADFlow求解器内无量纲化后的值。从中可以看出预测结果的翼型上表面全部处于分离状态，这可以解释计算得到的升力系数偏低的原因。图3展示了计算得到的升力系数Cp分布与实验结果的比较。由图可知，原始SA模型计算得到的吸力平台远低于实验观测值。

图2 原始SA模型的流场图Fig.2 Flow field of original SA model

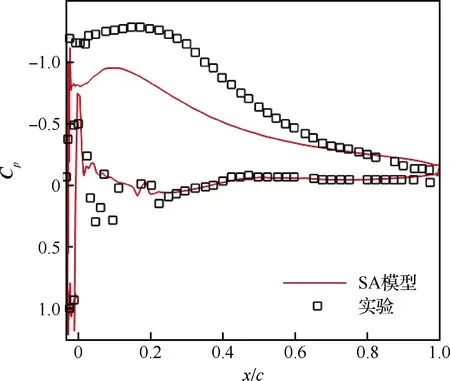
图3 计算得到的Cp分布与实验结果的比较Fig.3 Comparation of Cp distribution by computation and experiment

2.1.2 结果分析

在最简单的情形下，结冰翼型流场反演所用到的实验数据仅为CL，修正量β的先验分布是均值为1、方差全场相等的高斯分布。此时的目标函数可写为

(22)

图4展示了流场反演的目标函数、翼型升力系数随迭代次数的变化。在仅仅14步以内，SA模型经过流场反演就能以～10-8的精度拟合实验的CL，这说明SA模型在本文的修正框架下具有准确预测结冰翼型分离流动的潜力，同时显示了所使用的离散伴随方法的高效性。

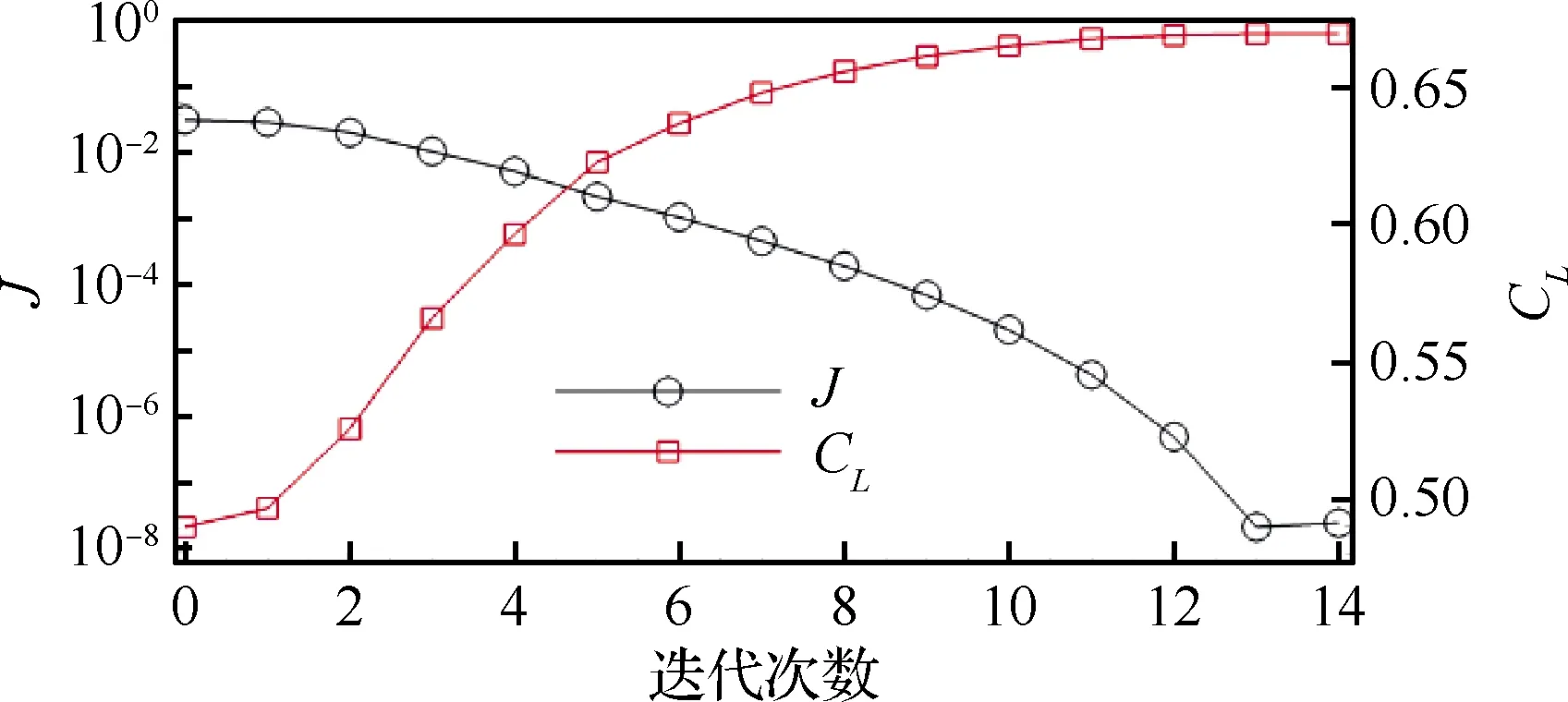
图4 流场反演的目标函数、翼型升力系数随 迭代次数的变化Fig.4 Variation of object function and lift coefficient of airfoil with iterations during field inversion

图5(a)展示了流场反演得到的最终流场。由图可知，流场反演之后所计算出的分离泡长度由整个翼型上表面缩短为约43%弦长。图5(b)展示了流场反演所得到的修正量β的分布。从图中可以看出，修正区域主要位于翼型上表面的分离剪切层中，且分为2个较为明显的部分。第1部分是在分离泡前部、剪切层起始的位置，该区域内的生成项乘子被减小；第2部分位于靠后的位置，此区域内的生成项乘子被增大。此修正结果表明，在结冰翼型分离流动预测中，误差最主要来源于分离剪切层。在剪切层的起始部分，SA模型倾向于高估涡黏性；而在剪切层的后半部分，SA模型则倾向于低估涡黏性。这与李浩然等[29]的结论一致：减小剪切层前部的涡黏性有助于模拟分离泡内从层流向湍流转捩的过程，而增大剪切层后部的涡黏性有助于模拟该处湍流的非均衡特性，增加剪切层内的湍流掺混，从而促进分离泡再附。这表明，流场反演能够以数据驱动的方式，仅利用有限的观测信息，正确推断出整个流场范围内对湍流模型不确定量所应做出的修正。

图5 以CL作为目标进行流场反演得到的 最终流场及修正量分布Fig.5 Final flow field and distribution of corrections of field inversion with CL as object

图6展示了流场反演得到的翼型表面压力分布与实验结果的比较。由图可知，虽然流场反演得到的升力系数与实验结果高度一致，但压力分布形态仍存在一定差别。从Cp的分布形态上可以推测得出，流场反演得到的分离泡长度更短，且分离泡再附位置的形状更陡峭。出现这种差异的原因是，流场反演本质上是基于数据驱动，把当前的先验和观测数据信息向整个流场进行泛化，所得到的流场仅是基于当前信息下概率最大的流场。相比于未修正的计算结果，这个流场与真实流场更为接近，但仍存在一定的差别。

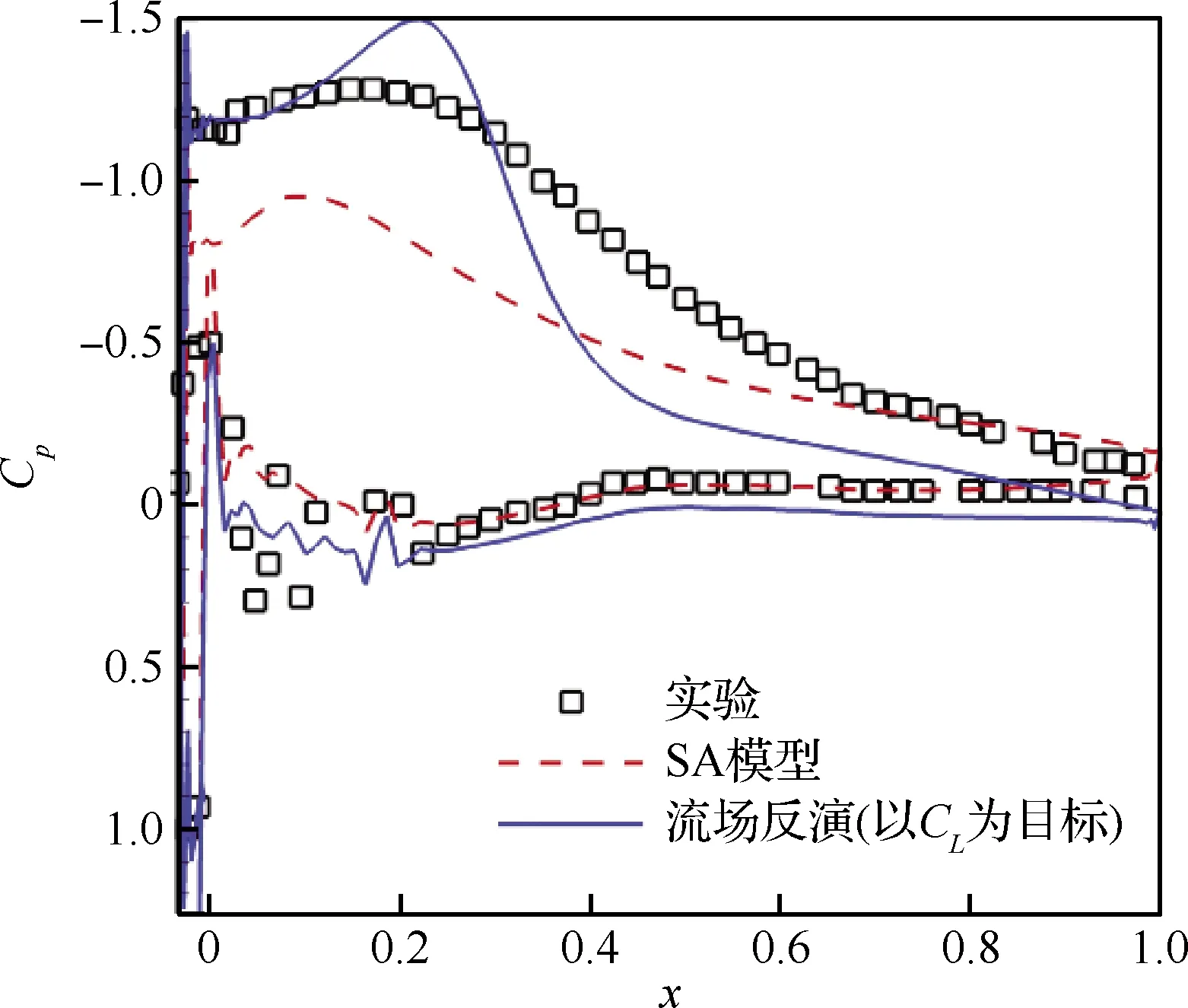
图6 以CL作为目标进行流场反演得到的翼型表面 压力分布与实验结果的比较Fig.6 Comparation of surface pressure distributions of airfoil between field inversion with CL as object and experiment results

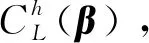
(23)

式中：λ为一个超参数，由经验给定。用于反演的Cp数据点全部位于压力分布光顺的部分，而排除了翼型前缘不光滑的结冰区域。图7、图8展示了该情况下流场反演的结果。从图中可以看出，除了翼型上表面前缘的小部分区域外，反演得到的流场在翼型大部分位置的Cp都与实验符合较好。与之对应的是分离泡的长度也有所加长，且再附位置的分离泡形状更加平缓。这表明，在为流场反演增加了新的可观测数据信息之后，流场反演的结果能够更加接近真实流场。

图7 以CL、Cp作为目标进行流场反演得到的 压力分布与实验结果的比较Fig.7 Comparation of pressure distributions between field inversion with CL and Cp as objects and experiment results

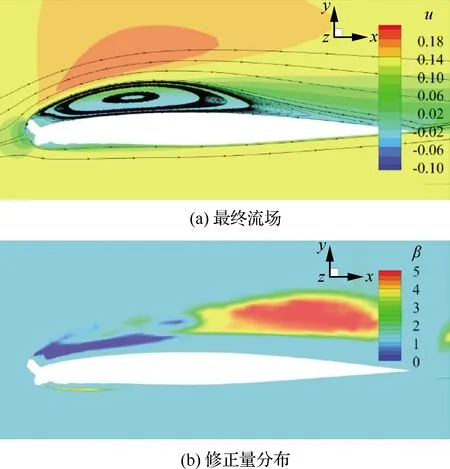
图8 以CL、Cp作为目标进行流场反演得到的 最终流场及修正量分布Fig.8 Final flow field and distribution of corrections of field inversion with CL and Cp as objects

2.2 周期山分离算例

2.2.1 算例介绍

周期山算例是另一个具有大分离流动特征的算例，由于其有大量实验和DNS数据，故被广泛用于测试CFD模型[6]。本文所计算的周期山模型几何及网格如图9所示，流向和法向的网格数分别为81和77。在本文所研究的工况下，基于山顶高度H和山顶截面上的平均速度Ub的雷诺数Reb=5 600。

图9 周期山模型几何及网格Fig.9 Geometry model and computation grid of periodic hill

周期山的上下壁面使用等温固壁边界条件，进出口使用周期边界条件。为了保证雷诺数一定，需要保证山顶处的质量流量一定。为此，给全场施加一个均匀的体积力场，体积力沿x轴正方向。在CFD计算过程中，由程序根据当前的质量流量自动调整体积力的大小，使其达到目标流量。

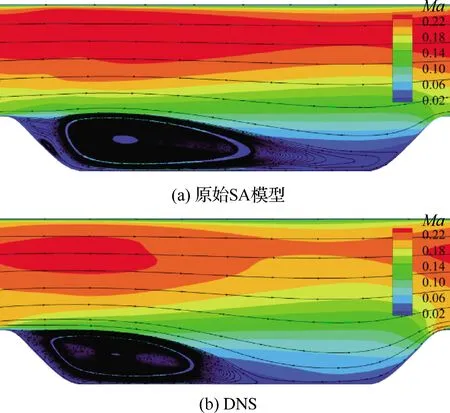
图10 原始SA模型的计算结果与DNS结果的对比Fig.10 Comparation between computation results of original SA model and DNS

(24)

本文的周期山算例具有质量流量约束，因此需要使用1.3节中的约束增广伴随方法。为了验证约束增广伴随方法的高效性，本文同时测试了使用和不使用该方法进行流场反演的2种方法，并进行结果对比。方法1使用该方法，由CFD程序进行定质量流量计算，由离散伴随给出定质量流量下目标函数对β的梯度，由优化算法更新β。方法2使用普通伴随，把体积力作为一个设计变量，CFD程序在给定体积力下进行计算，由离散伴随给出目标函数对β和体积力的梯度，把质量流量作为优化问题的约束，由优化算法更新β和体积力。

2.2.2 结果分析

图11展示了使用2种方法流场反演的收敛结果。由图可知，使用约束增广伴随方法能在1/4的迭代步数内达到与使用普通伴随同样的收敛效果。这说明对于带物理约束的优化问题，使用约束增广伴随方法的确能大大提高优化效率。从质量流量的变化曲线来看，约束增广伴随方法的质量流量始终等于目标流量，而普通伴随的质量流量在很长一段时间内在目标流量上下波动，这说明普通伴随的很多迭代都位于不满足约束的设计空间内，因此大大降低了优化效率。

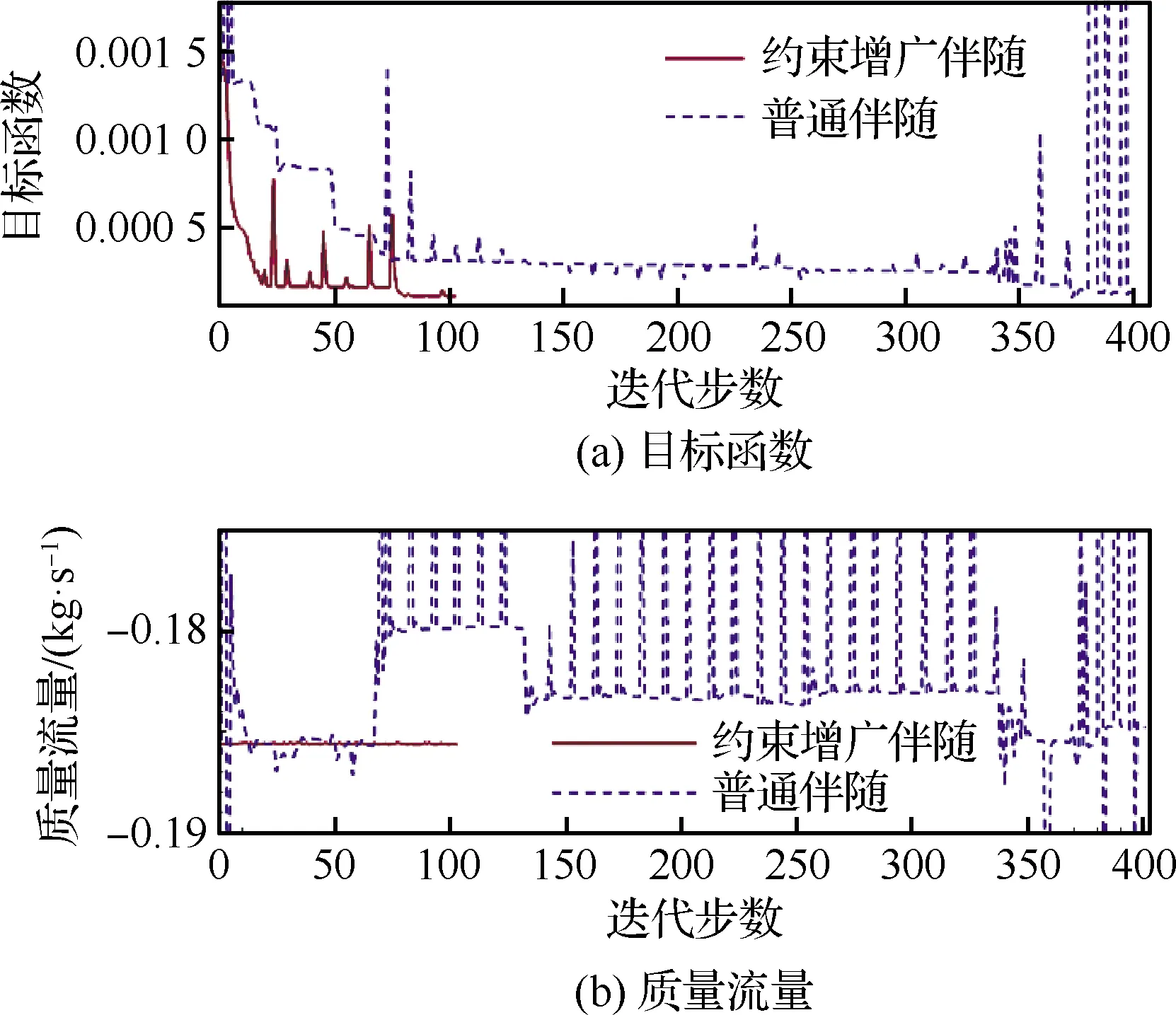
图11 使用/不使用约束增广伴随的周期 山流场反演收敛情况Fig.11 Convergence history of flow field inversion of periodic hill with/without constraint augmented adjoint method

图12(a)比较了原始SA模型、DNS，以及2种流场反演方法得到的周期山表面Cf分布。由图可知，原始SA模型与DNS的计算结果存在较大差别，而无论是否使用约束增广伴随方法，流场反演都能准确拟合指定的观测数据。图12(b)展示了原始SA模型、DNS，以及2种流场反演方法得到的空间不同截面的速度分布，其中x和y都以山顶高度H进行无量纲化；马赫数的横向尺度被放大6倍以便于观察。由图可知，流场反演得到的速度分布在流场底部与DNS符合较好，但在流场上部则与DNS有一定的差别，且2种伴随方法的结果之间也有一定误差，但相比SA模型有较大的改进。

图12 原始SA模型、DNS以及2种流场反演方法得到的周期山表面Cf分布和空间不同截面速度型分布Fig.12 Cf distributions on surface of periodic hill and velocity profile distributions at different sections computed with original SA model, DNS and two methods of field inversion

图13展示了2种方法得到的流场与修正量云图。由图可知，与原始SA模型相比，流场反演得到的分离泡再附位置均有所提前，这与DNS的结果一致。然而，流场反演得到的分离泡形状与DNS结果相比有一定的差别。另一方面，虽然2种方法的修正区域大致相同，但具体修正量也存在一定的区别。

图13 2种方法得到的流场与修正量云图Fig.13 Contours of flow field and corrections computed with two methods

综合以上结果可知，流场反演具有多解性，即在准确拟合指定的观测数据的基础上，可能存在不同的全场修正量分布。本文中的多解性是由伴随优化的局部最优特性造成的。流场反演的多解性同时表明，流场反演本质上是数据驱动的对先验和观测信息的泛化，其目的是得到当前信息下概率最大的一种可能的流场，它可能与真实流场仍存在一定差别。由于本文所用到的实验数据仅为周期山下壁面的Cf分布，因此反演得到的下半部分流场相比上半部分更能拟合真实流场。如何让流场的反演得到的结果从整体上更接近真实流场，而不仅仅是拟合指定的观测数据，仍是一个有待研究的问题。

3 结 论

传统的SA模型在计算结冰翼型分离流、周期山流动等具有大分离的流动时往往不能较为准确地进行预测。本文基于数据驱动的思路，假设SA模型的误差来源于其涡黏性输运方程的生成项所乘的系数，使用基于离散伴随的流场反演框架，根据有限的实验数据对该系数在全场的分布进行修正。对结冰翼型分离流、周期山流动2个流动问题进行了研究，得到了以下结论：

1) 无论指定拟合的观测数据是升力系数，压力分布，还是壁面摩阻系数分布，流场反演均能以相当高的精度修正模型使其预测值与指定的实验值吻合。

2) 流场反演能够将有限的观测数据信息泛化到整个流场，从而得到对整个流场的修正。更多的观测数据有助于流场反演得到更接近真实值的流场。

3) 作为一种数据驱动的方法，流场反演能够仅使用极其有限的实验数据，正确推断出对SA模型所要进行修正的区域及修正量。这为进一步的湍流模型改进提供了参考。

4) 周期山算例表明，本文采用的约束增广伴随优化的效率是普通伴随的4倍以上。这为今后其他带有物理约束的流场反演或气动优化问题提供了高效的解决思路。

5) 周期山算例展现了流场反演的多解性。这表明，流场反演本质上得到的是概率最大的可能结果，这一结果总体上更接近真实流场，但其具体取值则取决于给定的先验及观测数据，同时也受流场反演所用的优化算法特性的影响。

本文研究结果表明，作为一种数据驱动的湍流建模方法，基于离散伴随的流场反演能够从有限的实验数据中推断得到整体流场以及修正量分布。这可以进一步为基于机器学习的模型增强提供学习目标，也能对传统的湍流建模提供重要参考。