基于深度强化学习的固定翼无人机编队协调控制方法

相晓嘉，闫超，王菖，尹栋

国防科技大学 智能科学学院，长沙 410073

近年来，随着传感器技术、无线通信技术以及智能控制技术的不断发展与进步，无人机(Unmanned Aerial Vehicle，UAV)在军事和民用领域得到了广泛的应用，并取得了显著的成功[1]。但受限于平台功能少、有效载荷轻、感知范围小等固有缺陷，单架无人机在复杂环境下执行多样化任务仍面临较大困难[2]；而多架无人机组成协同编队能够有效弥补单机性能的不足，大幅提高系统的整体性能，在执行复杂作战任务时有着诸多优势[3]，如区域覆盖范围广、侦查和搜救成功率高等，作战效能远远高于各自为战的无人机。在可以预见的未来，随着战场环境和作战任务的日趋复杂，无人机编队将是执行作战任务的主要载体[4]。因此，无人机编队协调控制技术业已成为无人机系统技术领域的一个研究热点。

国内外学者针对该问题进行了广泛的研究。现有的解决方法，如模型预测控制[5]、一致性理论[6]等通常需要平台和扰动的精确模型进行控制率设计。但是，这一模型通常具有复杂、时变、非线性的特点，加之传感器误差、环境扰动等随机因素的影响，往往难以精确建模[7-8]。这严重限制了传统分析方法的适用范围。作为一种代替方法，应用无模型强化学习方法解决上述矛盾得到了越来越多的关注。

强化学习[9-10](Reinforcement Learning，RL)是机器学习领域的一个重要分支，主要用于解决序贯决策问题。强化学习任务通常可用马尔科夫决策过程(Markov Decision Process，MDP)来描述，其目标是在与环境的交互过程中，根据环境状态、动作和奖励学习一个最佳策略，使智能体(Agent) 选择的动作能够从环境中获取最大的累积奖励。强化学习可以不依赖于环境模型，适用于未知环境中的决策控制问题，在机器人领域已取得了大量较为成功的应用，如路径规划[11-12]、导航避障[13-14]等。

目前，已有研究人员将强化学习融入其编队协调控制问题的解决方案中，并在仿真环境下对方案的可行性和有效性进行了初步的验证。强化学习在协调控制中的应用研究最早由Tomimasu等[15]开展，在该仿真研究中，Agent采用Q学习算法和势场力方法学习聚集策略。不久之后，Morihiro等[16]基于Q学习算法提出了一种多智能体自组织群集行为控制框架。仿真试验表明，Agent在完成群集任务的同时，也表现出了反捕食行为以躲避捕食者。近年来，La等[17-18]相继发布多项有关集群协调控制的研究成果，该团队提出了一种将强化学习和群集控制相结合的混合系统，并通过仿真和实验验证了系统的可扩展性和有效性。该系统由低层集群控制器和高层RL模块组成，这一结合方式使系统能在保持网络拓扑和连通性的同时躲避捕食者。混合系统中的RL模块采用Q学习算法，并通过共享Q表的方式实现分布式合作学习。试验结果表明，该方式可加速学习过程，并能获取更高的累积奖励。Wang等[19]基于深度确定性策略梯度(Deep Deterministic Policy Gradient，DDPG)算法，提出一种无人机编队协调控制算法，使无人机能够在大规模复杂环境中以完全分散的方式聚集并执行导航任务。

上述应用均采用质点Agent模型，所得控制方案仅适用于旋翼无人机。与旋翼无人机不同，由于固定翼无人机飞行动力学的非完整约束，固定翼无人机编队协调控制更加复杂，需要采用有别于旋翼机的控制策略与方法。此外，固定翼无人机更易受空速、侧风等环境扰动的影响，在动态不确定环境中学习到的策略会随着环境的变化而变化，导致强化学习算法难以收敛。到目前为止，将强化学习算法应用于固定翼无人机编队协调控制中的研究成果依然较少。

Hung等[8,20]对该问题进行了初步的研究：2015年，其在无模型强化学习的背景下，研究了小型固定翼无人机在非平稳环境下的聚集问题[20]；该研究采用变学习率Dyna-Q(λ)算法学习Leader-Follower拓扑下的协调控制策略；仿真结果表明，所提变学习率方法具有更快的收敛速度；此外，所提方法还通过学习环境模型、并用规划的方式产生大量的模拟经验提高采样效率、加快学习过程。2017年，Hung和Givigi又在此基础上进一步提出了面向随机环境的无人机群集Q学习方法[8]；该研究以小型固定翼无人机为研究对象，基于无模型RL提出了固定翼无人机协调控制框架；在该框架中，Agent采用变学习速率Q(λ)算法在Leader-Follower拓扑中学习群集策略，并对抗环境的随机扰动；非平稳环境中的仿真试验验证了算法的可行性。

上述基于强化学习的固定翼无人机编队协调控制方法仍有一些问题尚未得到妥善解决：为解决维度灾难问题，Hung等[8,20]将状态空间离散化以缩减状态空间的维度。这种处理方式虽然降低了问题的求解难度，但却未必十分合理。此外，Hung等[8,20]仅在数值仿真环境对算法进行了初步的验证，所提算法的实用性和泛化性仍需进一步验证。

本文在Hung等[8,20]的研究基础上，聚焦动态不确定环境下固定翼无人机编队协调控制问题，基于深度强化学习算法构建端到端协调控制框架，实现多架无人僚机自主跟随长机组成编队协同飞行。首先，将ε-greedy策略与模仿策略相结合，提出ε-imitation动作选择策略以更好地平衡探索和利用；然后，结合双重Q学习和竞争架构对深度Q网络(Deep Q-Network，DQN)算法进行改进，提出ID3QN(Imitative Dueling Double Deep Q-Network)协调控制算法以提高学习效率；最后，构建高保真半实物仿真系统验证算法的有效性和可迁移性。

1 背景介绍

1.1 强化学习

在强化学习中，智能体以试错的方式不断地与环境进行交互，旨在学习一个最佳策略，使得其从环境中获取的累积奖励达到最大[21]。强化学习问题可用MDP框架形式化描述。通常情况下，MDP可用一个四元组(S,A,P(s,s′,a),R(s,s′,a))定义，其中S表示状态空间；A表示动作空间；P(s,s′,a)表示状态转移概率函数(模型)，该模型定义了智能体执行动作a∈A后，环境状态s∈S转移到新状态s′∈S的概率；R(s,s′,a)表示回报函数，其含义为智能体执行动作a∈A后，环境状态s∈S转移到新状态s′∈S所带来的奖励。

在智能体与环境交互中的每一时间步t，智能体观测环境状态为st，进而根据策略π(at|st)从动作空间A中选择动作at。执行动作at后，环境状态以P(st+1|st,at)的概率转移到新状态st+1，并将回报值rt反馈给智能体。智能体的目标在于学习一个最优策略π*:S→A，即状态空间到动作空间的映射，以最大化期望折扣回报Rt：

(1)

式中：T为终止时刻；γ为折扣因子，用于平衡未来回报对累积回报的影响，0≤γ≤1；rt表示t时刻的立即回报。

1.2 Q学习与深度Q网络

Q学习(Q-learning)算法是强化学习领域最为经典且最为重要的算法之一，是由Watkins和Dayan[22]提出的一种无模型(model-free)异策略(off-policy)的强化学习算法。该算法定义了Q值函数(Q-value)，并使用如式(2)和式(3)所示的更新规则迭代优化Q值函数：

Q(st,at)=Q(st,at)+αδt

(2)

(3)

式中：δt为TD(Temporal-Difference)误差；st为当前状态；at为当前动作；st+1为执行at后的环境状态；rt+1为立即回报值；α为学习率，0<α<1。

Q值函数一旦确定，即可根据Q值函数确定最优策略：智能体以贪婪策略选择动作，即在每一时间步选择最大Q值定义的动作。Q学习算法实现简单、应用广泛，但依然面临“维度灾难”的问题。该算法通常以表格的形式存储Q值，并不适用于高维或连续状态空间中的强化学习问题。

为解决“维度灾难”问题，利用深度神经网络(Deep Neural Network，DNN)作为函数逼近器估计Q值成为一种替代方案。Mnih等[23]将卷积神经网络(Convolutional Neural Network，CNN)和经验回放技术引入Q学习算法，提出DQN算法，在Atari游戏中达到了人类玩家的水平。较之于Q学习算法，DQN除了使用CNN作为函数逼近器并引入经验回放技术提高训练效率外，还设置单独的目标网络来产生目标Q值，以提高算法的稳定性[23]：

(4)

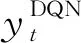
DQN通过最小化损失函数

(5)

即主网络输出的估计Q值与目标网络输出的目标Q值之差来实时更新主网络参数θ。与主网络实时更新参数不同，目标网络参数每隔若干时间步更新一次。具体而言，每隔N时间步，将主网络参数复制给目标网络，从而完成目标网络参数θ-的更新。

1.3 双重Q学习与竞争架构

DQN使用单独的目标网络产生Q值。尽管该技巧降低了预测Q值(主网络输出)与目标Q值(目标网络输出)之间的相关性，在一定程度上缓解神经网络近似值函数时出现的不稳定问题，但Q值“过估计”[24]的问题仍然没有得到解决。为更好地分析这一问题，将式(4)展开，有

(6)

显然，DQN的max操作使用相同的值函数(同一套参数θ-)进行动作选择和动作评估。这极易导致过高地估计Q值。为解决这一问题，Van Hasselt等[25]提出了双重DQN算法(Double DQN，DDQN)。该算法使用两个不同的值函数(两套参数)解耦动作选择与策略评估。DDQN的目标Q值可表示为

(7)

式中：θ为主网络参数，用于选择最优动作；θ-为目标网络的参数，用于评估该动作的价值。

除目标Q值的形式不同外，DDQN均与DQN保持一致。Atari游戏中的实验结果表明，DDQN能够更精确地估计Q值，获得更稳定有效的策略[25]。

(8)

式中：V(s)为状态值函数；|A|为动作空间A的维度。

竞争架构可以简便地融入DQN或DDQN算法中。实验结果表明，基于竞争架构的DQN算法能够获得更好的结果[26]。

2 问题描述

在想定的协调控制场景中，无人机编队采用Leader-Follower拓扑，即一架长机带领若干架僚机组成编队遂行任务。长机的控制策略由飞行员根据具体任务类型(跟踪、侦察等)和战场态势确定。长机通过通信链路将自身位置与姿态信息广播给僚机，僚机需要根据机载传感器感知到的自身状态信息和接收到的长机状态信息，实时选择最佳的控制指令(如滚转角)。假设僚机在不同固定高度层飞行，故不必考虑飞机之间的避碰问题[8,20]，因此不同僚机可使用相同的控制策略。每一架僚机均配备有自驾仪，每隔1 s[8,20]，控制策略根据当前系统状态输出新的控制指令，并发送给自驾仪，自驾仪使用PID控制器完成控制指令的底层闭环控制。

目标是让僚机在无任何先验知识的情况下，学习一种自主跟随长机编队飞行的控制策略。该策略能够根据获取的自身及长机的状态信息，确定当前给定状态的最佳滚转角设定值(自驾仪据此设定值完成闭环控制)，维持僚机与长机之间合理的位置关系(即僚机在以长机为中心的圆环内，如图1所示)，以实现Leader-Follower拓扑下的无人机编队协调控制。

图1 长机与僚机期望位置关系Fig.1 Positional relationship between leader and followers

2.1 无人机运动学模型

试错学习是无模型强化学习重要的特征之一。由于无人机的特殊性，在真实环境中进行试错是不现实的，且在高保真的仿真环境下进行学习亦需要花费大量的时间。为提高学习的效率，思路为根据真实飞机运动学的经验特性，考虑环境扰动建立无人机运动学数值模型，并以此为基础应用深度强化学习方法学习无人机编队的协调控制策略，进而将该策略应用(迁移)到真实世界。

在真实世界，无人机运动学通常由六自由度模型描述。考虑到无人机保持定高飞行，该模型可简化至四自由度。为了弥补简化带来的损失，同时考虑环境扰动的影响，故而在滚转、空速等各个子状态引入随机性[27]，所得随机无人机运动学模型为

(9)

由于随机性的影响，无人机在同一初始状态下执行相同动作会产生不同的终止状态。如图2所示，初始时刻，无人机位于原点(x=0,y=0)，并朝向+x方向(ψ=0)，执行同一控制指令后，无人机可能位于完全不同的位置。这说明所建运动学模型中引入的随机项能够模拟真实世界的随机性。

图2 随机性对无人机状态影响Fig.2 Collection of possible resulting UAV states due to stochasticity

2.2 协调控制MDP模型

在无模型强化学习的背景下，将无人机编队协调控制问题建模为马尔可夫决策过程。依次对该模型的3个要素，即状态表示、动作空间和回报函数进行定义。

2.2.1 状态表示

由式(9)可知，无人机的状态可以通过四维数组ξ:=[x,y,ψ,φ]表示。在Leader-Follower拓扑下的编队协调控制问题中，长机与僚机之间的相对关系(如距离、航向差等)对于控制策略的制定有着至关重要的影响。假定ξl:=[xl,yl,ψl,φl]代表长机状态，ξf:=[xf,yf,ψf,φf]代表僚机状态，若定义系统联合状态为s:=[s1,s2,s3,s4,s5,s6]，则

(10)

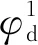
需要指出的是，不同于文献[8,20]，本文没有对状态空间进行离散化以简化问题，而是直接在连续状态空间中求解无人机编队协调控制问题。

2.2.2 动作空间

如前所述，无人机的操控通过改变滚转角设定值实现。控制策略每隔1 s更新一次滚转指令，间隔时间内由自驾仪完成底层闭环控制。考虑到无人机的最大加速度，并避免滚转角的剧烈变化影响无人机的安全飞行，定义滚转动作空间a∈A为

(11)

(12)

式中：a为选定的滚转动作；[-rbd,rbd]为无人机滚转角的范围。

2.2.3 回报函数

在强化学习中，设计合理的回报函数至关重要。参考文献[28]设计的成本函数，定义回报函数为

(13)

式中：r为立即回报值；d1和d2分别为圆环的内半径和外半径(以长机为中心，见图1)；d为僚机到圆环的距离；ω为调整因子，用以调整d的权重；ρ为长机与僚机之间的距离。

图3为长机与僚机相对位置关系对回报函数的影响。可知，当僚机位于以长机为中心的圆环内时，回报函数值最高；在圆环外部，当僚机靠近或远离长机时，回报函数值降低。这与图1所描述的场景想定是一致的。

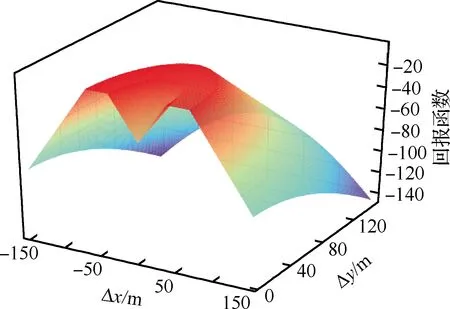
图3 长僚机相对位置与回报函数的关系Fig.3 Relation between position of follower relative to leader and reward function

3 ID3QN协调控制算法

DQN算法结合了深度学习和强化学习的优势，能够较好地处理高维连续状态空间下的RL问题。因此，该算法在机器人领域得到了广泛的应用[29-30]。结合双重Q学习和竞争网络，在DQN算法的基础之上进行，提出ID3QN算法，并应用该算法解决连续状态空间中无人机编队的协调控制问题。

3.1 动作选择策略

为提高训练阶段D3QN的学习效率，将ε-greedy策略与模仿策略相结合，提出ε-imitation动作选择策略平衡探索与利用。所谓模仿策略，是指僚机模仿长机行为(滚转指令)、参照长机的状态信息选择自身的滚转指令。ε-imitation动作选择策略的主要实现步骤见算法1。

该策略降低了初始阶段僚机的盲目性，减少了无效探索的次数，增加了经验池中正样本的数量，有助于训练效率的提升。

3.2 D3QN网络结构

为准确地估计Q函数，构建如图4所示的D3QN网络模型。该网络以系统联合状态为输入，输出为所有有效动作的Q值。上述D3QN由两个子网络组成：多层感知机和竞争网络。多层感知机包含3层全连接层(Fully-Connected，FC)，隐含节点数分别为64、256和128，均使用ReLU激活函数[31]。竞争网络包含两个支路：状态值函数支路和优势函数支路。状态值函数支路和优势函数支路均包含两层全连接层，两支路第1层全连接层的隐含节点数均为64，亦使用ReLU激活函数[31]。状态值函数支路第2层全连接层的网络节点数为1，输出值为当前状态的值函数；而优势函数支路第2层全连接层的网络节点数为3，输出值表示动作空间中3个待选动作的优势函数。D3QN(Dueling Double Deep Q-Network)输出层的输出为当前状态下各个待选动作的Q值，其值可通过“聚合”两支路的输出值得出。“聚合”操作的计算公式由式(8)定义。

图4 D3QN网络结构Fig.4 Network structure for D3QN

3.3 算法实现

采用ID3QN算法实现固定翼无人机编队协调控制，训练过程如图5所示。僚机被映射为RL中的智能体，智能体在与环境的不断交互中学习控制策略，更新网络参数。僚机获取长机的状态信息及自身的状态信息，组成联合系统状态s输入到D3QN网络中，ε-imitation动作选择策略根据D3QN的输出选取僚机的滚转动作a；分别将长机(长机的滚转动作随机产生以增加系统的随机性)和僚机的滚转指令输入随机无人机运动学模型，得到长机和僚机下一时刻的状态；回报函数值r和下一时刻系统状态s′亦可随之得出。交互过程中所产生的元组数据(s,a,r,s′)均被保持到经验池中。在每一时间步，从经验池中进行随机采样，批次更新D3QN的网络参数。当每回合的时间步达到一定步数，结束该回合，重新开始下一回合的学习。基于ID3QN的协调控制算法的主要实现步骤见算法2。

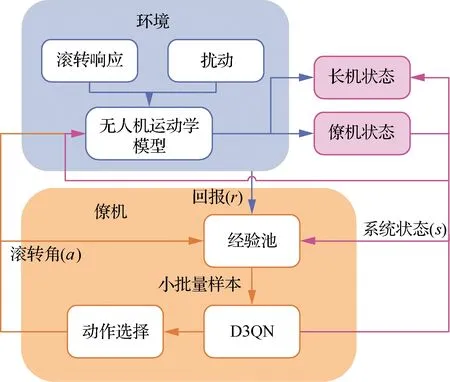
图5 ID3QN协调控制算法训练框图Fig.5 Block diagram of ID3QN coordination control algorithm

算法2 ID3QN算法输入:单回合最大时间步Ns;最大训练回合数Nmax1: 初始化经验池D(最大容量为N);随机初始化D3QN主网络参数θ;初始化目标网络参数θ-←θ2: repeat (for每一回合)3: 随机初始化系统状态s←ξl,ξf,φld ;t=14: whilet ≤ Ns do5: 根据ε-imitation动作选择策略(算法1)选取僚机滚转动作a6: 由式(12)计算僚机滚转角设定值φfd7: 将控制指令φfd应用到无人机运动学模型(式(9))中,生成僚机下一时刻状态ξ'f8: 观测下一时刻长机的状态ξ'l和滚转角设定值φ'ld9: 由式(10)构建系统状态s'←(ξ'l,ξ'f,φ'ld)10: 根据式(13)计算立即回报r11: 将状态转移数据元组(s, a, r, s')保存到经验池D中12: 若经验池溢出,即D>N,则删除D中最早的经验数据13: 从经验池D中随机抽取Nb个样本(sj,aj,rj,sj +1)(j = 1, 2, …, Nb)14: 计算每一元组数据的目标Q值:yj=rj+γQ(sj+1,argmaxa' Q(sj+1,a';θ);θ-)15: 根据损失函数更新主网络参数θ:L=1Nb∑jyj-Q(sj,aj;θ)216: 朝向主网络更新目标网络参数θ-:θ-←τ θ+(1-τ)θ-(τ为软更新率)17: s←s';[ξl,ξf,φld]←[ξ'l,ξ'f,φ'ld];t←t+118: end while19:until最大训练回合数

4 仿真验证及性能分析

4.1 参数设置

在Python环境中基于TensorFlow框架构建D3QN网络。D3QN的网络参数均使用Adam优化算法进行更新，batch size(Nb)设为32。共进行50 000回合的训练，每回合的仿真时间为30 s， 即最大训练回合数Nmax=50 000，每回合的最大时间步Ns= 30。需要指出的是，在正式训练前进行200回合的预训练，用于收集经验数据以进行批次训练。在训练过程中，探索率ε在10 000 回合内从初始值1.0线性衰减到最小值0.1； D3QN主网络参数的学习率α与目标网络的更新率τ从初始值(0.010, 0.001 0)指数衰减到最小值(0.001, 0.000 1)，衰减频率为1 000回合，衰减率为0.9，即每隔1 000回合衰减为原来的0.9倍。 训练过程中所需参数的经验值详见表1。

表1 ID3QN参数设置Table 1 Parameter settings for ID3QN

4.2 数值仿真实验

4.2.1 训练结果分析

为对策略进行有效的评价分析，使用单位回合内(如Ne回合)每一时间步的平均回报GAve作为度量标准来评价策略的优劣，其定义为

(14)

式中：r为立即回报，由式(13)确定。

为验证提出的ID3QN协调控制算法的可行性和有效性，分别使用DDQN、D3QN和ID3QN算法进行对比实验。其中，D3QN使用ε-greedy动作选择策略，其他流程与ID3QN完全相同；DDQN与D3QN算法流程完全相同，二者唯一的区别在于网络结构的不同：D3QN多层感知机分为两个支路分别估计状态值函数和优势函数，而后通过式(8)定义的“聚合”操作产生Q值，而DDQN仅构造单个支路的全连接层直接近似Q函数。为保证对比实验的公平性，上述3种算法均使用相同的深度网络结构(见图4，DDQN没有进行拆分操作，仅有1个支路)和参数设置(见表1)。 在整个训练过程中，每隔100回合(即Ne=100) 记录一次平均回报GAve的值，上述3种算法的学习曲线如图6所示。

由图6可知，在训练初期，3种算法的回报曲线均快速上升；在大约10 000回合的训练后，3种算法获取的平均回报逐渐趋于稳定。DDQN与D3QN的回报曲线几乎重合，这意味着两种算法具有大体相当的性能；而在训练初期，D3QN的回报曲线增长速度略高于DDQN，这表明竞争网络可以更有效地学习Q函数。与以上两种算法相比，ID3QN算法无论是在初始阶段还是在收敛阶段都能够获取最高的平均回报；这意味着在ε-imitation动作选择策略的引导下，ID3QN算法能够更快更有效地学习最佳策略。

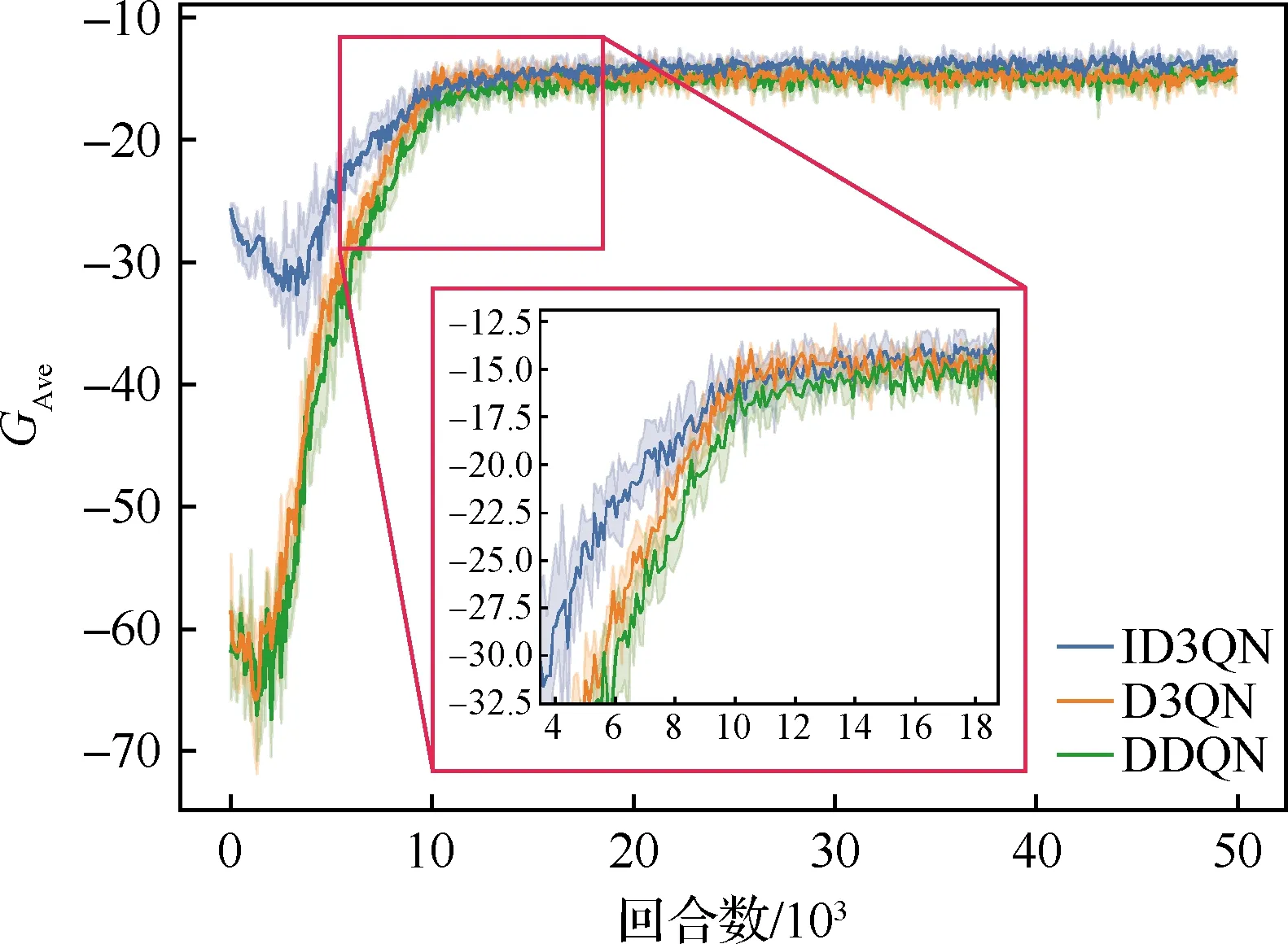
图6 3种算法的学习曲线Fig.6 Learning curves of three algorithms

4.2.2 测试结果分析

完成4.2.1节的训练过程后，对训练后的协调控制策略进行测试分析。测试实验中，两架僚机与一架长机组成编队。每隔1 s，长机随机选择滚转动作，而僚机根据训练后D3QN网络的输出选择最大Q值所对应的滚转动作。实验中，最大时间步(Ns)设置为120，即仿真时间为2 min。编队的飞行轨迹见图7，飞行过程中立即回报值r、僚机与长机之间的距离ρ和航向差Δψ的变化曲线情况见图8。

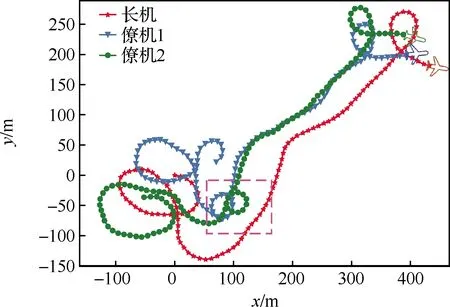
图7 数值仿真中ID3QN策略的测试结果Fig.7 Testing results of ID3QN policy in numerical simulation

图8 数值仿真中ID3QN策略的性能曲线Fig.8 Performance curves of ID3QN policy in numerical simulation

图7直观地展示了ID3QN协调控制策略的效果。无论是在前期和后期的转弯阶段，还是在中期的平直飞行阶段，两架僚机均能较好地跟随长机飞行。值得注意的是，在55 s左右，两架僚机均位于长机前方且距长机较远。在之后的十多秒内，两架僚机通过大滚转角机动实现了绕圈飞行(见图7紫色方框内)。这是因为滚转角是僚机唯一的控制量，两架僚机只能通过盘旋来缩小与长机之间的距离。在之后的飞行中，僚机可以维持与长机之间的距离在70 m上下，航向差大致在±25°的范围之内。

除以上的定性评价外，继续进行定量测试以进一步分析所得协调控制器的有效性。在定量测试实验中，4架僚机分别使用3.1节提出的模仿策略和4.2.1节训练得到的DDQN、D3QN和ID3QN 3种控制策略跟随长机协同飞行。实验共进行100回合，每回合的仿真时间(Ns)设为120 s。在每回合的实验中，长机的初始状态和滚转指令随机产生。为保证测试实验的公平性，4架僚机的初始状态随机产生并保持一致。4种策略的测试结果见表2。

由表2可知，3种基于DQN的深度强化学习算法(即DDQN、D3QN和ID3QN)获得了远高于模仿策略的平均回报；同时，3种算法所得平均回报的方差远低于模仿策略。这意味着基于DQN的无人机编队协调控制策略具有良好的可行性和稳定性。大体来看，3种策略所获取的平均回报相差不大，ID3QN所得平均回报略高。与D3QN和DDQN相比，ID3QN策略的方差最低，这意味ID3QN具有更好的鲁棒性。上述结果表明，提出的ID3QN算法的性能优于D3QN和DDQN算法。

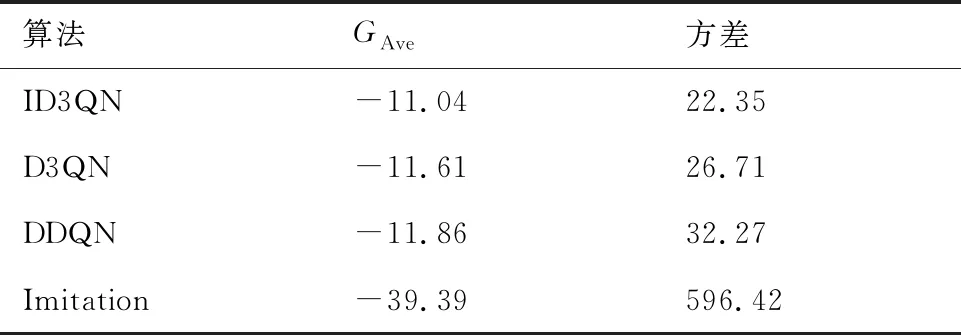
表2 测试阶段4种策略性能对比

4.3 硬件在环实验

为展示所提ID3QN协调控制算法的泛化能力和应用价值，基于X-Plane 10飞行仿真器建立高保真半实物仿真系统进行硬件在环实验，验证所得策略的实用性。

4.3.1 半实物仿真系统

如图9所示，搭建的高保真半实物仿真系统由地面控制站、飞行仿真器、自动驾驶仪和机载处理器组成：

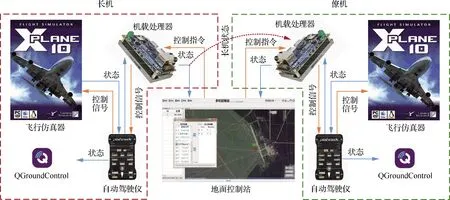
图9 高保真半实物仿真系统Fig.9 High-fidelity semi-physical simulation system

1) 使用课题组开发的多机控制站SuperStation作为地面控制站，完成对多架无人机的控制，如模式切换、航线规划等。

2) 使用商业飞行模拟软件X-Plane 10作为飞行仿真器，X-Plane 10能够模拟风速变化、天气变化等环境扰动。

3) 选择PIXHAWK作为自动驾驶仪的硬件平台。

4) 使用英伟达Jetson TX2作为机载处理器。

长机和僚机共享一个地面控制站，即地面站可以同时监控长机和僚机。二者的机载处理器通过RJ45网线连接，模拟机间无线通信链路。

协调控制软件架构如图10所示，选用PX4开源飞控作为PIXHAWK自动驾驶仪的软件栈。ID3QN协调控制策略运行在TX2上，TX2上安装有Ubuntu 14.04操作系统和机器人操作系统(Robot Operating System，ROS)。TX2与PIXHAWK/PX4通过MavLink协议连接。使用以下节点实现无人机编队的协调控制：

图10 协调控制软件架构Fig.10 Software architecture for coordination control

1) Communicator节点：通过UDP协议接收长机状态信息。

2) Flocking Commander节点：基于ID3QN算法完成上层协调控制。

3) Controller节点：通过PID控制器完成底层闭环控制。

4) MAVROS节点：通过MavLink协议同PX4建立连接获取自身状态信息。

4.3.2 实验结果分析

在半实物仿真实验中，一架僚机直接使用数值仿真环境中训练得到的ID3QN协调控制策略完成跟随长机飞行的任务。长机采用随机策略生成滚转指令，僚机根据训练后的ID3QN策略每隔1 s更新一次滚转指令，完成协调控制。二者的控制策略分别独立运行在各自的机载处理器上，二者的机载处理器通过网线连接，长机通过UDP协议将自身状态信息发送给僚机。半实物仿真实验流程如下：

1) 在MANUAL模式下使用地面站控制长机与僚机起飞。

2) 使用地面站控制飞机切入MISSION模式，两机按照预设航线飞行，并保持一定距离。

3) 使用地面站控制僚机切入OFFBOARD模式，僚机根据ID3QN策略完成跟随飞行任务。在每一时间步，Flocking Commander节点根据ID3QN策略更新滚转指令，决策过程如下：① 从Communicator节点获取长机状态(即位置、姿态和速度)信息，而后将其与从MAVROS节点获取的自身状态相结合，构建系统状态；② 载入数值仿真环境中训练得到的D3QN网络模型参数；③ 以 系统状态为输入，D3QN网络输出滚转指令，进而生成滚转角设定值；④ 向Controller节点发布滚转角设定值，该节点据此通过PID控制器完成底层闭环控制。

4) 一段时间后，使用地面站控制飞机切入RETURN模式，实验结束。

硬件在环仿真飞行实验共持续120 s，长机的滚转角设定值在-10°～10°之间随机产生，飞行速度设置为10 m/s。实验中长僚机的飞行轨迹、航向角和滚转角的变化情况见图11，飞行过程中的立即回报值r、长僚机之间的距离ρ和航向差Δψ见图12。在初始时刻，僚机与长机之间的距离高达110 m，且僚机位于长机的前方。在随后20多秒的时间内，僚机通过盘旋飞行成功将两机之间的距离缩短到75 m之内。这是因为滚转角是僚机唯一的控制量，僚机只能通过盘旋缩小其与长机之间的距离。在之后的飞行中，无论长机平直飞行还是机动转弯，僚机均能及时做出反应，稳定地跟随长机飞行。需要指出的是，训练得到的控制策略在用于半实物仿真环境下的仿真飞行实验时并没有进行任何的参数调整。上述结果充分表明，所提ID3QN算法训练得到的协调控制策略可直接迁移到半实物仿真环境中，具有较强的适应性及良好的实用性。

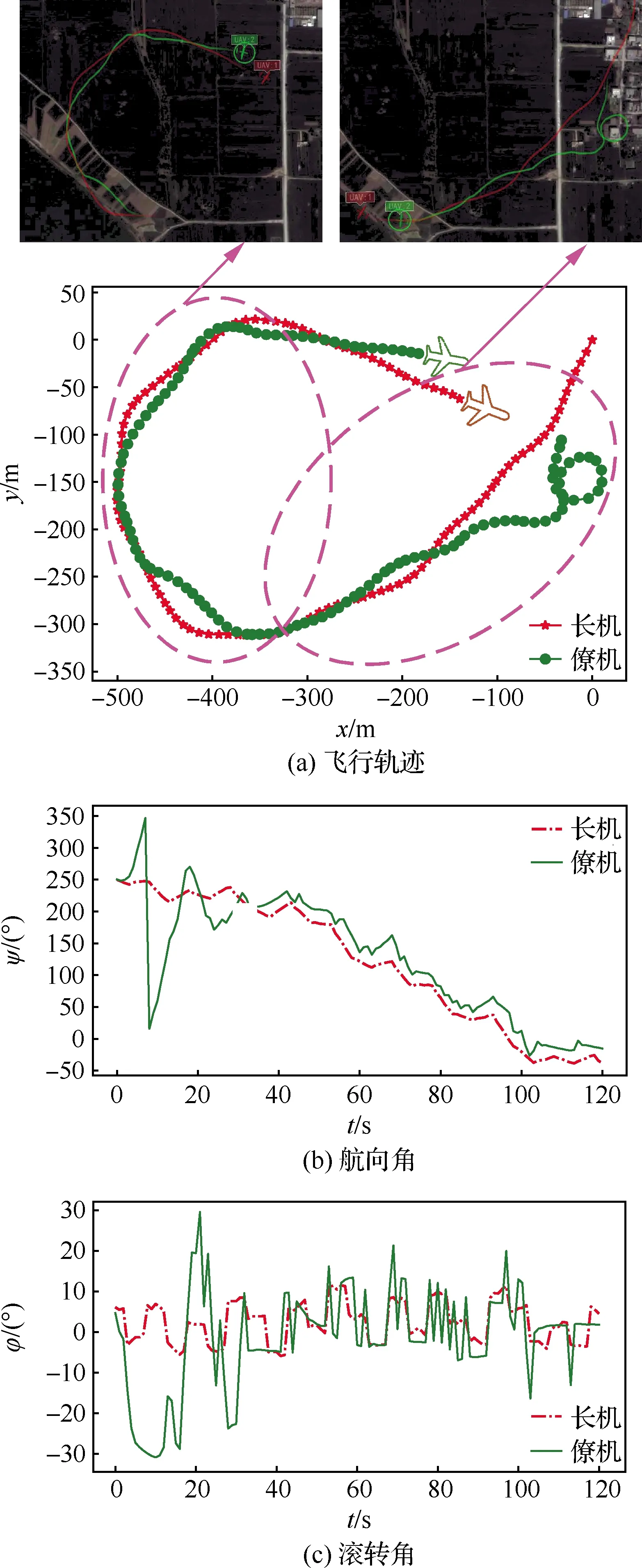
图11 硬件在环实验结果Fig.11 Results of hardware-in-loop simulation

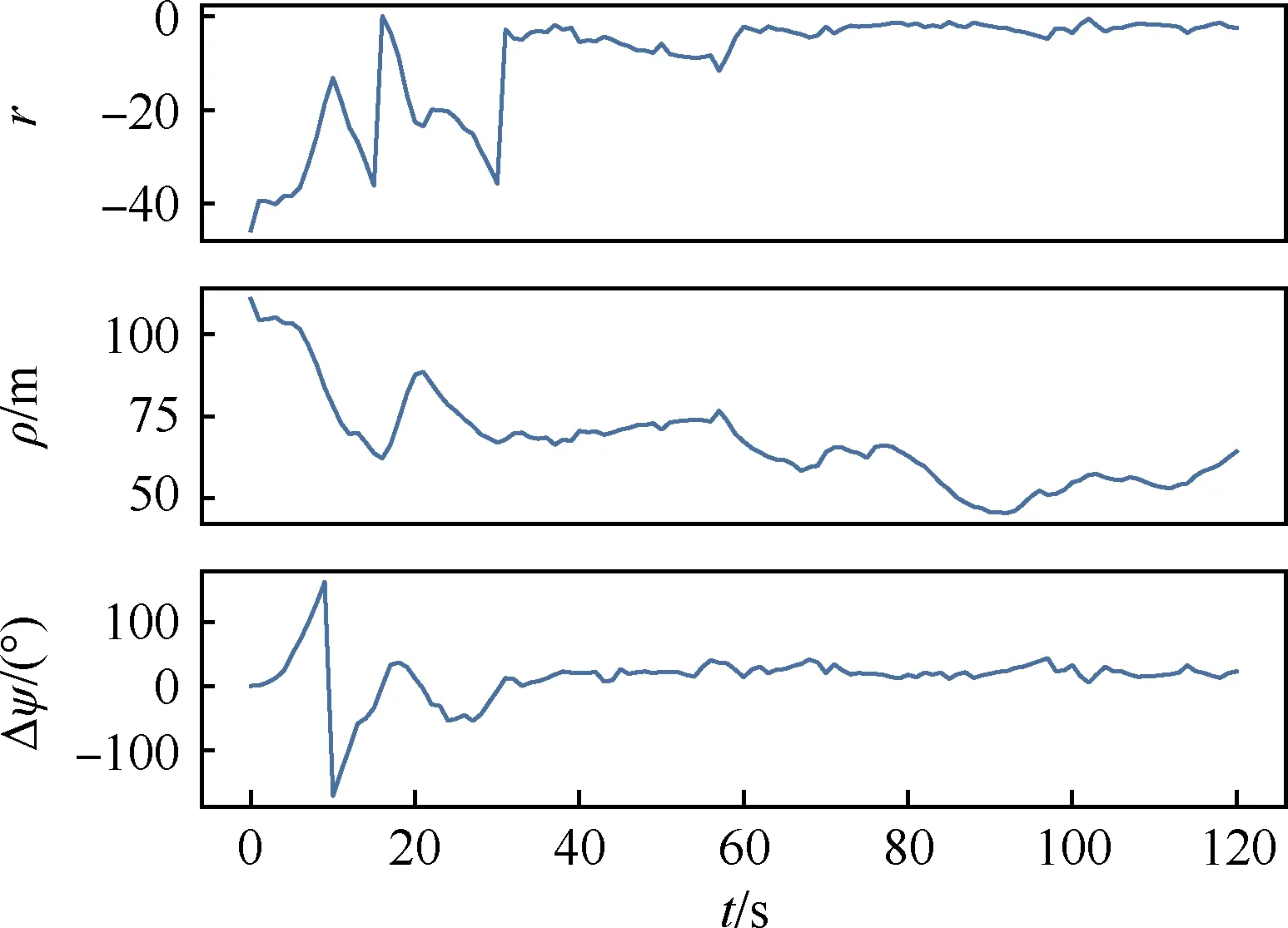
图12 硬件在环实验中ID3QN策略的性能曲线Fig.12 Performance curves of ID3QN policy in hardware-in-loop simulation

5 结 论

聚焦动态不确定环境下的固定翼无人机编队协调控制问题，基于深度强化学习提出了无人机编队协调控制方法。首先在强化学习背景下对无人机协调控制问题进行了形式化描述，建立了协调控制MDP模型。进而将ε-greedy策略与模仿策略相结合，提出了ε-imitation动作选择策略，并将其引入DQN算法，提出了ID3QN算法以提高算法的学习效率。数组仿真环境下的训练结果和测试结果明：在ε-imitation动作选择策略的引导下，ID3QN算法能够更快更有效地学习最佳策略。最后，构建高保真半实物仿真系统验证了算法的有效性和可迁移性。硬件在环飞行仿真实验显示，数值仿真环境下训练得到的控制策略无需任何参数调整即可直接迁移到半实物仿真系统中。这一结果表明，提出的ID3QN协调控制算法具有较强的适应性及良好的实用性。