基于深度学习的单排孔气膜冷却性能预测

李左飙，温风波，唐晓雷，苏良俊，王松涛

哈尔滨工业大学 能源科学与工程学院，哈尔滨 150001

气膜冷却技术作为一种简单有效的成熟冷却技术，被广泛运用于各种工业产品中。气膜冷却的基本原理是：在高温部件表面布置冷气孔或狭槽，冷却介质通过叶片内部的流道，经由孔或槽以横向射流的形式注入主流之中，并在主流的压力和摩擦力作用下弯曲附着在高温部件表面，形成温度较低的冷气膜，将壁面与高温燃气隔离开，同时带走部分高温燃气或明亮火焰对壁面的辐射热，对壁面起到良好的保护作用[1-2]。

气膜冷却最早来源于Wieghardt[3]的二维槽缝热气喷射研究，用于解决机翼防冻问题。20世纪70年代，气膜冷却开始被用于涡轮叶片上。早期研究者主要通过解析计算(Metzger[4]、Muska[5]和Gritsch[6]等)和设计实验(Goldstein[7]、Pedersen[8]以及Sinha[9]等)的方式分析气膜孔的冷却性能及其影响因素，为气膜冷却技术的发展提供了理论和实验支持。然而单纯的解析计算或实验的方式时间周期长，人力物力成本高，难以在大规模工业活动中应用。随着高性能计算手段的发展，基于数值模拟的计算流体力学(CFD)的方法得到了越来越多的重视。Walters和Leylek提出了适用于三维气膜冷却问题的数值模拟体系[10]，并将该体系应用于圆柱形孔和成型孔气膜冷却流场计算中[11-14]，通过与实验数据对比，验证了数值计算方法在气膜冷却性能预测上的可行性和准确性。Acharya等[15]总结了现有的各种数值方法对气膜冷却流动和传热的预测能力，表明大涡模拟(LES)和直接数值模拟(DNS)在预测结果方面表现得比湍流模型更好。目前，先行通过CFD筛选优化气膜孔布置方案，再进行模型实验仍是工程上的主流手段。

尽管CFD辅助设计结合实验的方法有效地节省了实验的成本，但是CFD建模和计算的复杂性仍会使得设计过程变得繁琐与费时。Muska[5]和Baldauf[16]等利用显式函数将气膜冷却效率的预测表达为一系列影响因素和气膜冷却效率间的映射关系，获得了气膜冷却效率的经验公式。这意味着，设计者可以通过调整特定的参数，快速评估和优化气膜冷却布局方案。但是，由于射流的复杂性，这些经验公式在一些情况下不足以表达变量与冷却效率之间的高维非线性映射关系。

近年来，深度学习技术的蓬勃发展吸引了流体力学领域工作者的关注。深度学习的方法具有较强的处理高非线性问题的能力，大量的研究表明深度学习同样适合用于处理复杂的流动问题。Guo等[17]使用卷积神经网络(CNN)对不规则几何的绕流流场进行了预测，准确率达到98%。Sekar等[18]使用卷积神经网络和多层感知器(MLP)将叶型几何参数化并预测了不同几何形状的叶型在不同来流攻角和雷诺数条件下的流动情况，准确率分别达到了99%和97%。陈海等[19]使用CNN对翼型气动系数进行了预测，获得了较好的拟合结果。廖鹏等[20]使用CNN对混合翼型的前缘压力分布进行了预测，可以得到和CFD计算机结果非常吻合的压力分布曲线。陈海昕等[21]梳理了机器学习技术在气动优化中应用的发展脉络，总结了机器学习在气动优化设计中的典型应用。

在气膜冷却相关领域，Wang等[22]使用最小二乘支持向量机(LS-SVM)对单排圆柱孔下游平板表面的侧向平均绝热气膜冷却效果进行了预测，秦晏旻等[23]使用BP神经网络对单排成型孔气膜冷却效率进行了预测，结果均表明神经网络的预测精度和范围都优于经验公式。Dolati等[24]研究了数据处理组合算法(GMDH)型神经网络在预测带有等离子体激励器的气膜冷却性能方面的应用，模型预测值与CFD数据基本一致，表明该模型可以为气膜冷却方案的设计提供有益的信息。Dávalos等[25]使用了人工神经网络(ANN)对燃气轮机叶片前缘区域平均气膜冷却效率(AAFCE)进行了预测，神经网络以0.003 8的均方根误差成功预测了AAFCE值，同时计算出影响气膜冷却效率的最主要因素为吹风比，相对重要性为40.36%。Milani等[26-27]使用随机森林(RF)的方法预测了气膜冷却计算模型的普朗特数(Pr)分布，优化了各向异性湍流模型，使其对气膜冷却过程中的热量传递计算更为准确。Yang等[28]使用条件生成对抗神经网络(cGAN)结合遗传算法(GA)，提出了非均匀来流温度条件的渗流冷却孔布局优化方法。

现有的关于气膜冷却问题的深度学习模型大多着眼于少数特定几何和来流条件，对于在较大几何和来流参数范围内都适合的泛用型深度模型的研究较少。针对这一问题，本文提出了一种基于深度学习的气膜冷却性能预测方法，使用多层感知器模型，输入气膜冷却孔的几何参数、来流参数和流场位置参数，经过深度人工神经网络运算，可以获得物面上绝热冷却效率的分布情况，验证了深度学习在处理差异度较大的样本数据时的泛化能力。利用这种方法，可以在初步设计阶段快速选择和评估合适的气膜冷却布局方案，提高了设计效率。

1 深度模型细节

深度学习是一类模式识别方法的统称，是机器学习算法中最热门的一个分支。关于深度学习的研究是在人工神经网络的基础上进行的。Hinton和Salakhutdinov于2006提出了深度学习的思想以及模型训练方法[29]，重新挖掘出了神经网络的潜力，将机器学习的研究再次推向高峰。深度学习的核心理论是万能逼近定理(Cybenko[30]，Hornik[31])，它声明了一个前馈神经网络如果具有线性输出层和至少一层有激活函数处理的隐藏层，只要给予足够数量的神经元，就可以以足够高的精度逼近一个在Rn紧子集上的连续函数。也就是说，如果两个有限空间之间存在连续的映射关系，那么，深度神经网络可以以能够接受的误差近似这个映射关系，完成从一个有限空间映射到另一个有限空间的任务。深度神经网络非常适合学习样本数据的内在规律和表示层次，因此被称为实现人工智能的基础。

深度学习的本质是参数估计，已知样本的分布寻找参数的最大似然估计。深度神经网络的核心是反向传播算法(Back Propagation algorithm, BP)[32]：神经网络通过各神经元的计算，将输入数据逐层向前传播，在输出层与标签数据进行对比，依据事先定义的损失函数计算误差，将误差对神经元中学习参数的梯度逐层向后进行反向传播，各层神经元根据梯度更新学习参数，反复执行参数更新迭代，直至误差达到精度要求。

1.1 特征参数的选取

深度学习的目的是从样本数据中提取特征参数空间X与标签参数空间Y之间的映射关系，因此特征参数和标签参数的选取是决定深度学习模型性能的基石。

本文建立的气膜冷却性能预测模型，目标是获取气膜冷却性能在受热表面上的分布情况。物理模型如图1所示，气膜孔直径D为12.5 mm，孔上游计算域流向长度为6.5D，下游计算域流向长度为24.5D，计算域横向宽度为3D，计算域垂直受热表面高度为10D，冷气管长径比为5。冷却性能的评价指标是绝热冷却效率ηad。其定义为

图1 物理模型Fig.1 Physical model

(1)

式中：T∞为主流温度;Taw为绝热壁面温度；Tc为冷气流温度。

将标签参数设置为ηad，由此关键在于特征参数的选择。

特征参数是标签参数的主要影响因素。气膜冷却的影响因素很多，一般认为，对于圆柱形气膜冷却孔，对冷却效率有较大影响的参数有孔的几何参数，包括气膜孔的喷射角度、孔径的大小、孔的长径比、孔的间距、孔的排数等；流动参数包括吹风比、冷气流与主流的密度比、动量比、主流马赫数、主流湍流度等。

几何参数中，描述气膜孔喷射角度和出口形状的参数包括倾斜角和复合角，喷射角度不同，冷气膜的生成质量和覆盖范围也会呈现明显的差异。Walters和Leylek[12]的研究表明，随着复合角的增加，气膜孔下游的旋涡对称结构被破坏进而形成一个单一的优势涡，使得绝热冷却效率横向分布更加均匀，但传热系数将增大。因此，倾斜角θ和复合角φ被选择作为输入特征参数。

关于长径比的影响，Lutum和Johnson[33]研究表明，当圆孔长径比大于5时，其对冷却效率没有影响。关于孔径的影响，由于气膜冷却计算中常采用以孔径为参照进行归一化的简化模型，孔径对于气膜冷却效率的计算结果没有影响。因此，不将孔径和长径比作为输入。

流动参数中，吹风比和密度比对于冷却效率的影响较为显著而且复杂。吹风比和密度比的数学定义为

(2)

(3)

式中：ρc和ρ∞分别表示冷气流和主流密度；Uc和U∞分别表示冷气流和主流速度。

Goldstein等[7]研究了吹风比对冷却效率的影响，结果表明，在0～2范围内，孔附近的冷却效率随吹风比增大先增大到一个峰值后减小，而在远离气膜孔的地方曲线变化则较为平缓。Pedersen等[8]研究了密度比对冷却效率的影响，研究发现，密度比小于1时，冷却效率随吹风比增大而呈现上升趋势，而当密度比增大时，冷却效率随吹风比的变化趋势与Goldstein等的结论一致，同时峰值随密度比增大而趋向于吹风比较小的值。Sinha等[9]的研究随后也证明了Pedersen等的结论。因此，吹风比M和密度比DR均被选择作为输入特征参数，尽管二者并非相互独立。而动量比I与前二者都不相互独立，并且当M和DR已确定时，I也是确定值，因此，动量比I不作为输入参数。

对于主流马赫数的影响，Gritsch等[34]的研究表明，高主流马赫数会对气膜冷却效率造成一定影响，但由于本文的计算均在亚声速情况下进行，此时主流马赫数对冷却效率的影响不大。因此，主流马赫数不作为输入参数。

本文采用的预测策略为基于多层感知器模型的逐点预测，即在物面计算域中选取网格节点作为数据点，对每个工况结果进行相近数目的采样，每个采样点存储该坐标位置的冷却效率。通过预测每个工况各采样点的冷却效率，进而获得整个受热表面的冷却效率分布情况。该方法是对目前流场学习中常用的基于卷积神经网络的图-图(Image-to-Image)方法的改进。基于图片的学习策略输入几何图形的图像，输出流场图像，结果直观，计算效率高，但计算精度受到输入图片质量的制约。另外，基于图片的学习方法在训练时无法同时兼顾到多种流动参数不同的工况，每个模型只能针对特定的流动条件进行预测，在实际应用中受限。基于多层感知器的逐点预测法不以图片而是以具体数据作为输入和输出，避免了因图像质量带来的精度问题，可以同时预测不同流动条件下的结果，能够方便快捷地提取流场中任意一点的数据，实际应用中更为灵活。逐点预测法要求在输入参数中加入归一化坐标变量x/D和y/D。

另外，考虑到时间成本与计算能力，本文不考虑孔间距、孔排数和主流湍流度的影响。

综上分析，最终得到的深度神经网络的输入参数为吹风比M，密度比DR，复合角φ，倾斜角θ，归一化坐标x/D和y/D；输出参数为绝热气膜冷却效率。

1.2 建立数据集

气膜冷却性能预测模型的数据集来源于CFD计算结果。为了验证当样本数据差异较大时，深度神经网络的学习和泛化能力，本文选取了大范围的参数建立样本数据集。几何参数倾斜角θ选取20°～60°范围内的11个值，每2个选取值间隔4°；复合角φ选取-16°～16°范围内的9个值，每2个值间隔4°。流动参数吹风比M选取0.5～ 2.0范围内的7个值，每2个值间隔0.25；密度比DR选取1.25～2.0范围内的4个值，每2个 值间隔0.25。参数互相组合，总计2 772组样本数据，每组数据选取约1.2×104个数据点，总计约3.3×107个数据条目。为了监测模型泛化性，及时调整网络超参数以提高模型性能，本文将数据集按照8∶2的比例划分为训练集和验证集。训练集数据用于模型的训练，验证集数据用于模型训练过程中的监测与调整。

本文还设置了测试集数据，用于判断模型是否发生了过拟合，评估深度模型在真实应用场景下的有效性。测试集数据的流动参数选择M=1.0，DR=2.0，几何参数倾斜角θ选取20°～60°范围内的21个值，每2个值间隔2°，复合角φ选择-16°～16°范围内的17个值，每2个值间隔2°，参数互相组合并去除主数据集中出现的元素，共258组样本数据，每组数据选取约1.2×104个数据点，总计约3.1×106个数据条目。

所有数据集在输入网络进行运算前需要进行归一化，使得所有参数均处于0～1范围内。归一化的目的是保证所有特征具有同等地位，以防止神经网络对某些特征过分偏重，造成学习结果的偏颇和失衡。另外，使参数处于0～1的范围则有利于网络参数的高效计算，使得待学习参数处于-1～1的小范围内，防止部分参数过大导致溢出。

1.3 数值模拟配置

使用CFD计算获取样本数据，前处理使用ICEM软件的批处理模式，批量生成计算网格，求解器使用FLUENT软件进行计算，后处理使用CFX-POST导出采样数据。计算网格细节如图2所示。

图2 计算网格细节Fig.2 Computational mesh details

主流和射流进口均采用速度进口，主流速度设定为20 m/s，调整射流速度改变吹风比。主流温度设定为300 K，调整射流温度改变密度比。出口边界采用压力出口条件，出口背压为大气压。计算域两侧面设置为平移周期性交界面，顶部设置为对称面，受热表面设置为绝热无滑移壁面。湍流模型选择Realizablek-ε模型，Pr为0.85，湍流强度为5%，湍流黏度比为10。

1.4 数值结果验证

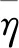
图3 M=0.5时样本数据的验证Fig.3 Validation of dataset for M=0.5

图4 M=1.0时样本数据的验证Fig.4 Validation of dataset for M=1.0

结果显示，带冷气箱的模型与文献[10]的数值结果接近，与实验数据相比数值均偏高，但本文的数值结果对冷却效率分布曲线轮廓的拟合要好于文献[10]。数值偏高的主要原因在于k-ε湍流模型采用了各向同性假设，对冷气与主流掺混过程中的质量和热量传递拟合精度有限。

尽管数据集中冷却效率数值偏高，但其随下游距离的变化趋势与实验数据拟合得较好。因此数值上的差异并不会对深度模型学习气膜冷却内在物理规律的能力造成明显影响，可以认为本文使用的数据集是有效的。具体结果将在第2节进行展示。

1.5 神经网络配置

本文的深度学习神经网络基于开源深度学习框架PaddlePaddle[35]进行搭建，它的优势在于简单和快速。

本文需要进行训练的数据集体量较为庞大，为了兼顾性能和计算效率，采用Mini-batch策略进行训练，即每次迭代时，只随机从原始数据集中抽取相同数量的小批量数据条目进行训练，每次抽取的数据不重叠，直至原始数据集中所有样本都进行了训练，完成一个训练轮次。批次数量过小时，会使得迭代时间过长，残差曲线剧烈振荡，难以收敛；批次数量过大时，由于反向传播过程中参与计算的是一个批次数据的平均梯度，会导致参数更新缓慢，降低训练效率。本文设置的批次数量较大，为1 024，即每次迭代抽取1 024个数据条目进行训练，以平衡训练耗时和数据交互耗时。

深度神经网络选用多层感知器模型，网络结构为8×800的全连接网络，即除了输入数据层和输出数据层，共布置了8个隐层，每个隐层包含800个神经元。相邻隐层间神经元完全连接，同一层神经元相互独立，互不连接。网络模型如图5所示。

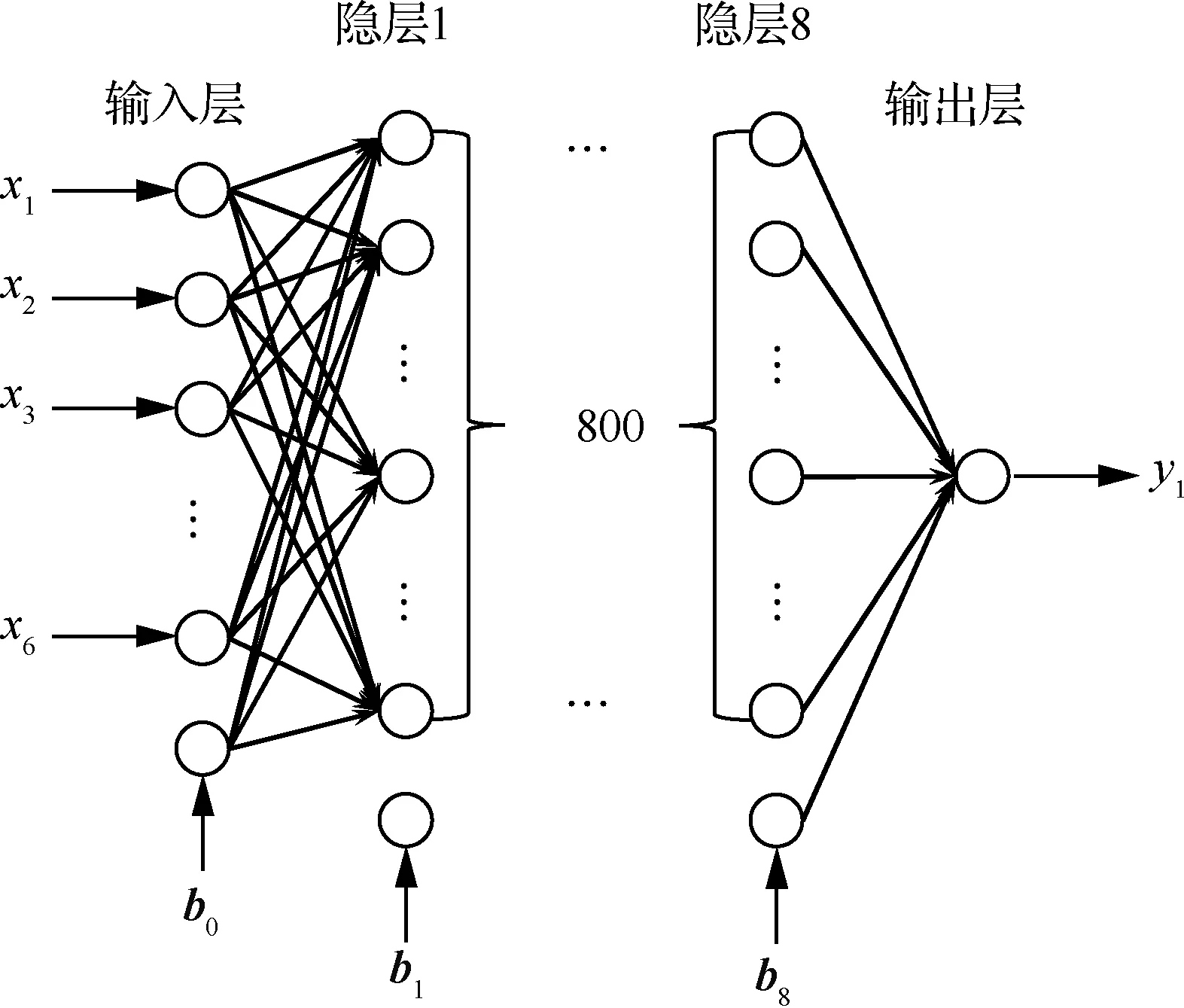
图5 MLP模型结构Fig.5 MLP model structure

隐层神经元将前一层各神经元的输出值进行加权求和，用激活函数进行非线性处理后输出，并作为后一层的输入值，用这样的方法层层进行特征提取和映射，建立由输入特征到输出标签的映射模型。各隐层内部的计算公式为

f(WiYi-1+bi)

(4)

式中：下标i表示第i层神经网络；上标n表示输入向量长度；上标m表示输出向量长度；Yi为第i层输出向量；Wi为第i层权重矩阵；bi为第i层偏置向量。

激活函数选择ReLU函数，其数学表达式如式(5)所示，函数图像如图6所示。ReLU函数作为线性函数，在计算性能上更具优势，同时能有效避免梯度消失问题。因此大多数深度学习模型中使用的激活函数是ReLU函数。

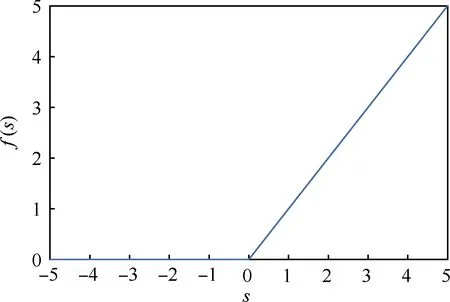
图6 ReLU函数Fig.6 ReLU function

(5)

损失函数选用均方差函数，其数学表达式为

(6)

优化器选用Adam算法(Kingma和Ba[36])，可以有效避免深度神经网络中的梯度爆炸现象。初始学习率设置为α=2.5×10-5，同时为了保证训练过程中残差的平稳下降，设置了学习率调度器，学习率随累计迭代步数(step)遵循自然指数规律率衰减，学习率计算公式为

(7)

式中：k为累计迭代步数；ψ为衰减系数；c为学习率衰减步长，一般设置为全数据集训练一轮(Epoch)所需的迭代步长的倍数。在本文中，ψ设置为0.5，c设置为训练10轮需要的步数。

2 模型性能与分析

模型经过105轮训练，共计2.64×106个迭代步后，残差稳定收敛，收敛曲线如图7所示。训练集误差最终收敛至2×10-5，验证集误差最终收敛至2.5×10-5，满足精度要求，因此认为深度模型有效，可以进行进一步的性能验证。

图7 训练过程残差曲线Fig.7 Residual curves during training process

2.1 准确性与泛化性分析

为了验证深度学习模型的准确性和泛化性，从训练集、验证集和测试集中各随机抽取一个工况，分别使用CFD和深度模型预测该工况下气膜冷却效率的分布云图，对比结果如图8～图10所示。

图8展示了训练集中样本的CFD计算结果和深度模型预测结果的对比，样本的几何参数为倾斜角θ=32°，复合角φ=16°，流动参数为吹风比M=1.25，密度比DR=2.0。图9展示了验证集中样本的CFD计算结果和深度模型预测结果的对比，样本的几何参数为倾斜角θ=28°，复合角φ=4°，流动参数为吹风比M=0.5，密度比DR=1.5。图10展示了测试集中样本的CFD计算结果和深度模型预测结果的对比，样本的几何参数为倾斜角θ=32°，复合角φ=14°，流动参数为吹风比M=1.0，密度比DR=2.0。

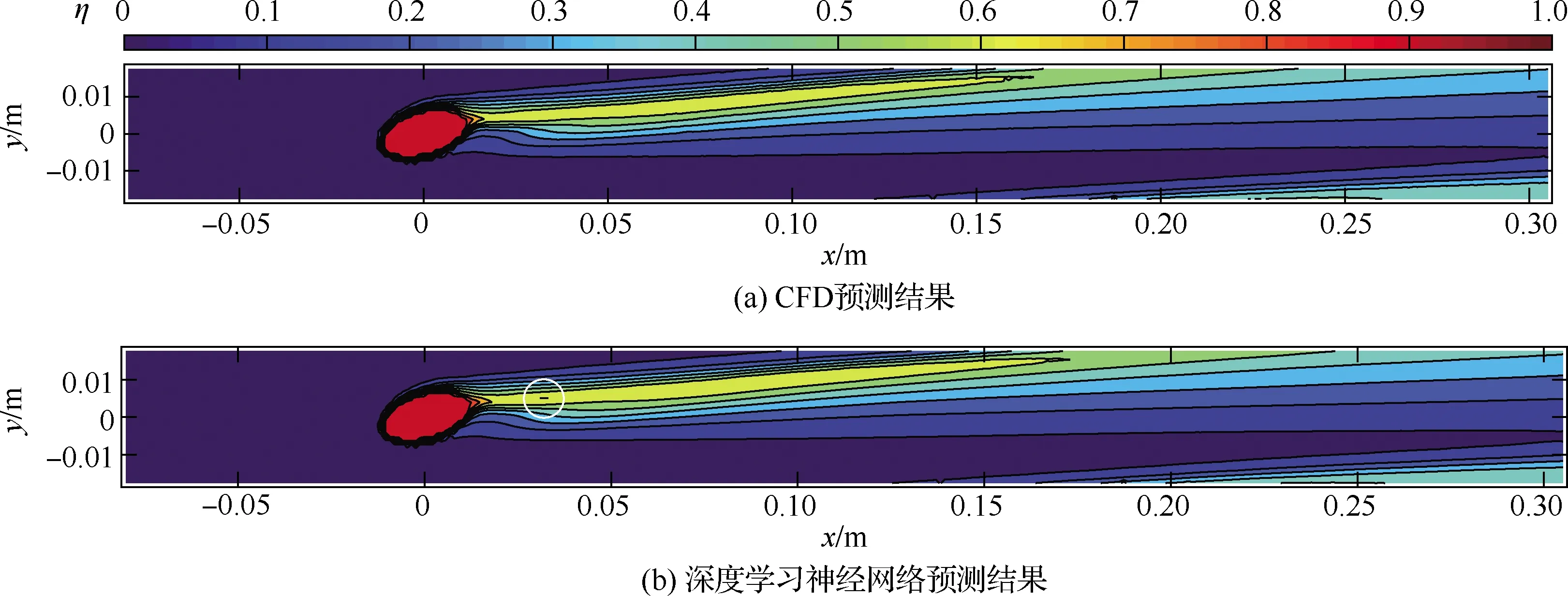
图8 训练集样本CFD结果与神经网络结果对比Fig.8 Comparison between prediction of CFD and MLP on training set

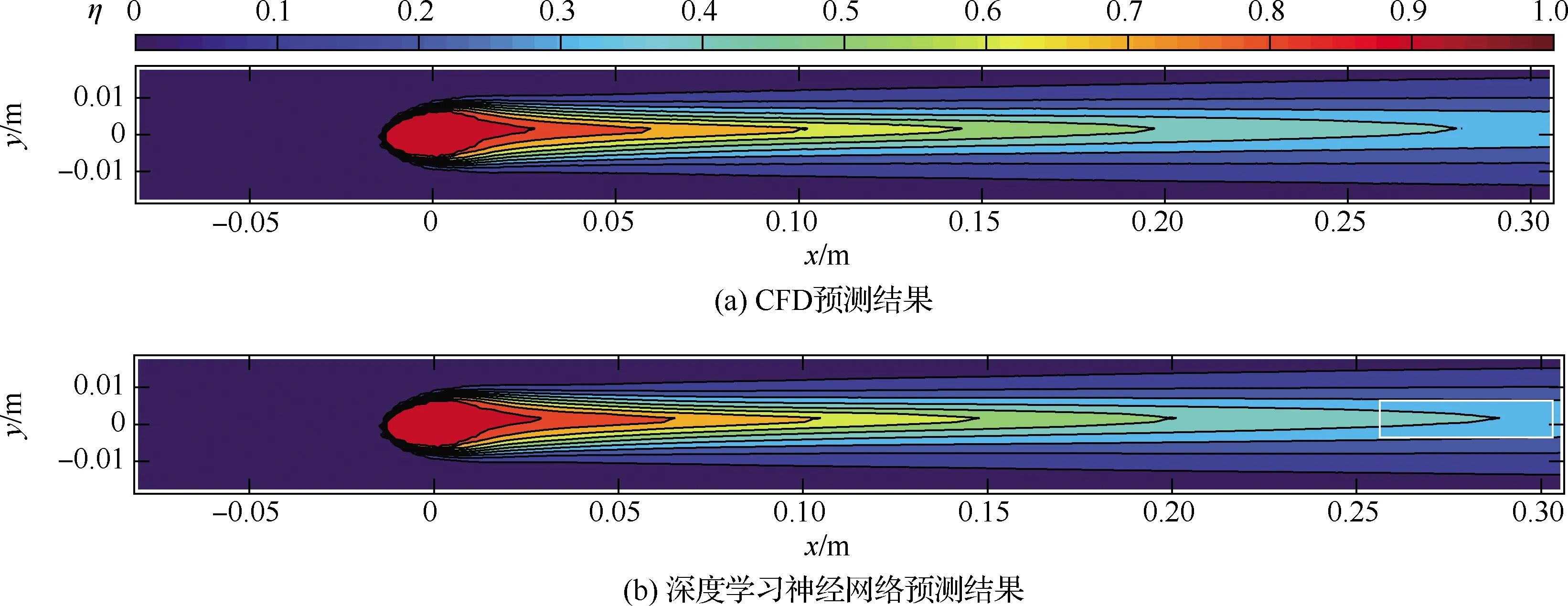
图9 验证集样本CFD结果与神经网络结果对比Fig.9 Comparison between prediction of CFD and MLP on validation set

图10 测试集样本CFD结果与神经网络结果对比Fig.10 Comparison between prediction of CFD and MLP on testing set

2.2 模型预测能力验证

为了进一步验证深度模型对于气膜冷却问题中内部物理规律的学习能力，本文选取了DR=2.0时，吹风比分别为M=0.5和M=1.0的中心线气膜冷却效率和侧向平均效率的预测值与数据集进行对比，如图11所示。可以看到，模型预测值与数据集的拟合程度是令人满意的，尤其对于M=1.0的工况，中心线冷却效率在气膜孔附近的明显转折也得到了很好的还原。

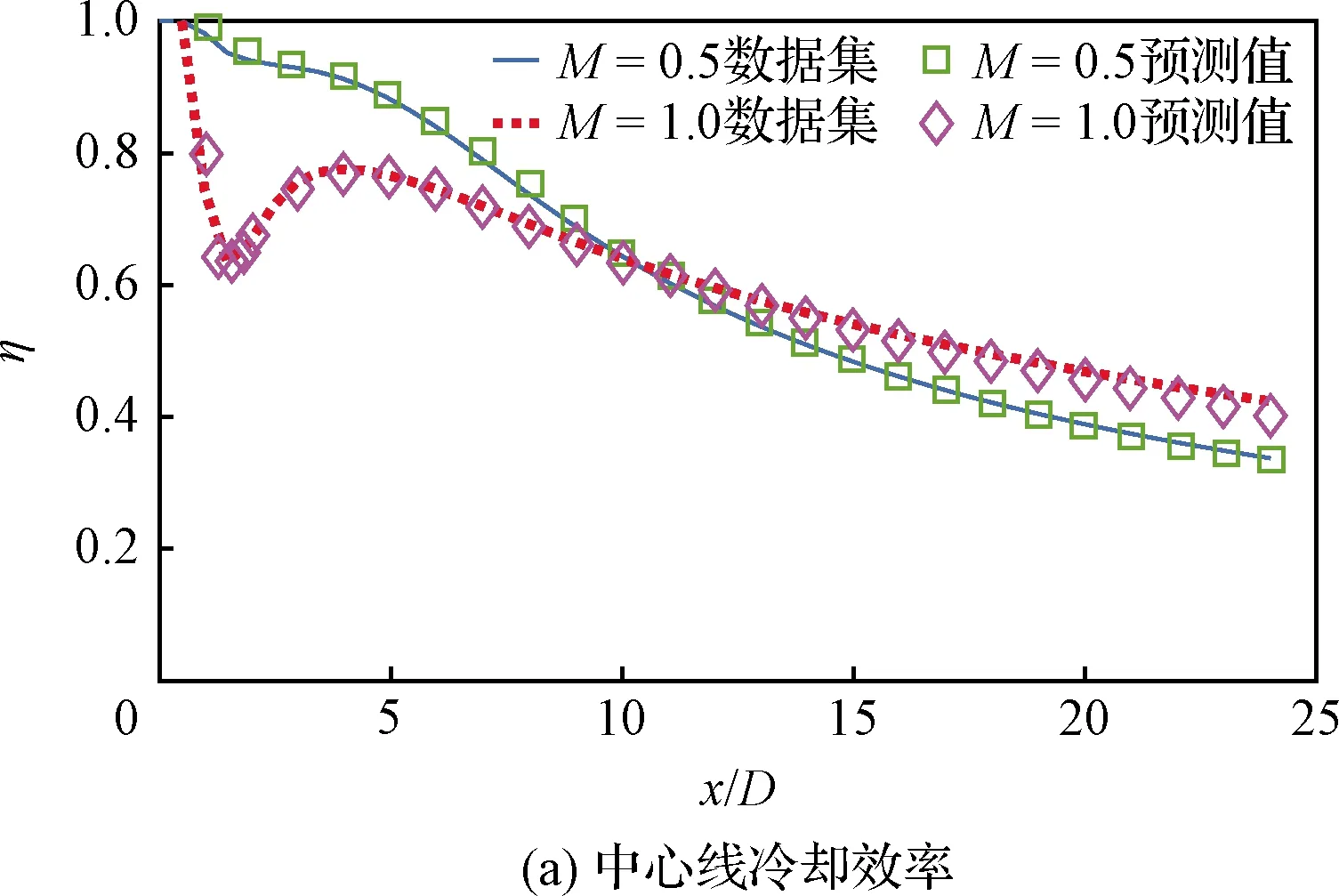
图11 CFD结果与神经网络输出的冷却效率对比Fig.11 Comparison between prediction of CFD and MLP in film cooling effectiveness

使用校正决定系数(Adjusted R-Square， AR2)定量评估深度模型预测的气膜冷却系数分布与CFD计算结果之间的拟合度。相对于决定系数(R-Square，R2)，AR2引入了样本数量n和特征数量p，抵消了样本数量对R2值的影响。值越大时，代表拟合度越高，深度模型的性能越好。R2和AR2的数学表达为

(8)

(9)

对每个工况样本计算校正决定系数，图12展示了训练集、验证集和测试集上所有工况样本的校正系数分布情况。可以看到，在训练集和验证集上，深度模型的拟合度均高于0.95，测试集上拟合度高于0.99，表明深度模型较好地建立了特征参数与绝热气膜冷却系数之间的映射模型，并具有足够的精确性和泛化性。

图12 深度模型校正决定系数Fig.12 Adjusted R-square of MLP

需要指出的是，尽管整体上深度模型的预测结果拟合度较高，但在局部细节处仍存在一定的误差，主要表现为出现局部坏点(图8圆圈)以及同等级冷却效率覆盖范围的扩大或缩小(图9和图10中矩形框)。较大的参数范围导致的较大样本差异度可能是造成误差的原因之一。CFD计算过程中的数据不稳定性以及数据采样过程中的插值误差也会在数据集中引入噪声。由于深度神经网络具有很强的拟合能力，因此可能在训练过程中出现噪声干扰现象，导致局部误差。

2.3 计算效率分析

CFD计算每个工况耗时约25 min，总计耗时约1 263 h。使用GPU训练深度学习模型时，每训练一轮耗时约18 min，总计耗时约32 h，而模型训练完成后进行预测时仅需约2 s。在满足足够精度要求的前提下，利用训练好的深度学习模型预测冷却效率分布的耗时仅为CFD计算耗时的1/1 000。

综上分析，与CFD方法相比，深度模型能以较高的精度和较好的泛化能力建立输入特征与绝热气膜冷却系数之间的映射模型，而耗时远少于CFD方法。

3 结 论

本文提出了一种基于深度学习的气膜冷却性能预测方法。利用CFD建立样本数据集，对多层感知器结构的深度神经网络进行训练和测试，建立包括几何参数、流动参数和采样点位置参数在内的输入特征参数与绝热气膜冷却效率之间的映射模型。对比分析了CFD数据和深度学习预测数据，得出以下结论：

1) 深度学习模型具有较高的精度和较好的泛化能力。在训练集和验证集上的校正决定系数大于0.95，测试集上的校正决定系数大于0.99。与CFD数据的拟合度较高。

2) 深度学习模型能够较好地学习气膜冷却问题中的隐含规律。模型预测的中心线冷却效率和侧向平均效率曲线能够较好地拟合数据集，对于一些特殊的转折和轮廓也能很好地还原。

3) 深度学习模型的结果云图可以较好地识别并还原CFD结果的整体轮廓，但在局部仍然存在一定的误差，给预测结果引入了一些噪声。将来的工作可以尝试使用更先进的模型算法，以提高深度模型的稳定性和抗噪性，降低过拟合程度。

4) 在满足足够精度要求的前提下，深度学习模型的预测耗时仅为CFD耗时的1/1 000，在预测速度上具有较大优势。将深度学习与CFD相结合应用于工程设计和优化中，可以大大提高工作效率，缩短设计周期，具有较好的应用前景。

当前方法忽略了主流湍流度、气膜孔间距比、孔排数以及受热表面曲率对气膜冷却效率的影响，同时使用了简化的物理模型，不能反映工程应用中的真实场景。因此，在接下来的工作中，将考虑更多的影响参数，缩小参数范围，使得建立的数据集更加接近工程实际，提高模型的工程应用能力。