传递函数在货车车架模态分析中的应用
刘丹,杨承阁,王志辉
(410000 湖南省 长沙市 湖南工业职业技术学院 汽车工程学院)
0 引言
随着载货汽车市场需求量的不断饱和,市场竞争日益激烈,为了占据更大的市场份额,各汽车厂家都力争降低生产成本,提高汽车的安全性和舒适性。车架作为汽车主要零部件之一,它所构成的框架不仅能保持车辆框架的扭转刚度以及支撑纵向载荷,而且还用以承受汽车上其他总成的质量[1],比如发动机、变速箱、货箱、燃油箱和驾驶室等。车架的强度、刚度及动力学特性直接影响了整车的基本性能。本文着重从货车车架模态结构出发,结合发动机到车架纵梁的传递函数,获得车架的优化模型,同时用传递函数进一步验证优化后结构的动态性能。
Lanczos 方法是20 世纪50 年代提出的,用正交向量组成的矩阵约化对称矩阵为三对角矩阵的方法,该方法对于求解大型稀疏对称矩阵的特征值来说是非常行之有效的方法。它的原理是,先产生一个三对角矩阵Tm,然后将问题转化为求这个三对角矩阵的特征值,这样就使问题变得相对简单。随着m 值的增大,Tm的最大与最小特征值会越来越接近原矩阵的最大与最小特征值。
文献[2]中验证了对于大规模特征值问题的求解,有限元Lanczos 法和ANSYS 中的Lanczos求解结果十分接近。本文中货车车架的模态计算采用ANSYS 完成。
1 Lanczos 算法[3]
对于n 阶实对称矩阵A,模态求解经常用到Lanczos 算法,其基本思想是先选取一个任意向量q1,并将其单位正交化处理,通过Lanczos 迭代过程构造一组正交化序列Q=[q1,q2,…,qn],则 QTAQ=T 就是一个对称的三对角矩阵。Lanczos方法的求解步骤主要包括:Lanczos 向量的生成和三对角矩阵特征问题的求解。
(1)给定初始Lanczos 向量q0=0,选择初始Lanczos 迭代向量q1,并关于质量矩阵进行正交化处理q1TMq1=1
(2)在第i 个Lanczos 向量已知的情况下,通过迭代计算第i+1 个Lanczos 向量:
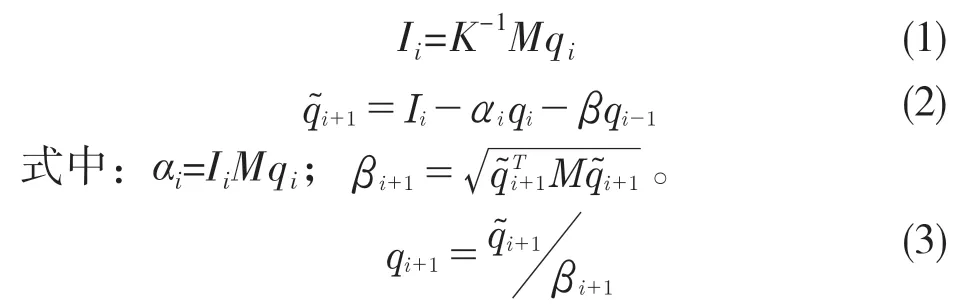
当βi+1→0 时,算法收敛。
(3)将原求解部分特征解Λr和Φr的广义特征值问题KΦr=ΛrMΦr转化为Lanczos 向量空间内三对角矩阵Tm的标准特征值问题

(4)求解标准特征值问题式(4),得到特征解 Z 和λ
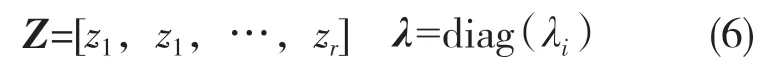
(5)计算原特征值问题的部分特征解

如果在Lanczos 迭代过程中出现了βi1=0,则迭代过程中断,这意味着,在第i1步之前出现了一个关于矩阵A=K-1M 的不变的子空间。由此,可以得到A 的前i1-1 个特征值。如果要继续求解其他的特征值,则需要重新给初始Lanczos 向量赋值,开始Lanczos 迭代过程。
2 传递函数原理
传递函数(Transfer Function)反映了系统对不同输入信号的传递能力,是描述动态系统特性的一种非参数估计模型,对任何线性系统来说,都可以应用传递函数在频域中直接分析系统的稳定性,对系统进行综合设计和校正。传递函数是描述系统动态特性的一种数学表达式,仅与系统参数m,k 和c 有关,从而在拉氏域中完整地描述了系统的动态特性。实际上,传递函数与单位脉冲响应函数是一个Laplace 变换对[4]。
初始条件为零的多自由度结构系统的运动微分方程可以表达为
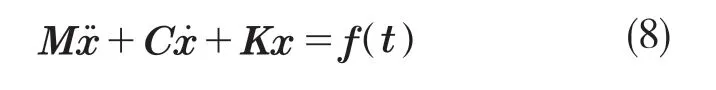
式中:M,C,K——质量矩阵、阻尼矩阵和刚度矩阵;f(t)——激振力向量;——结构系统的加速度响应、速度响应和位移响应向量。
对式(8)两边同时进行拉普拉斯变换得到在频域中的表达式:
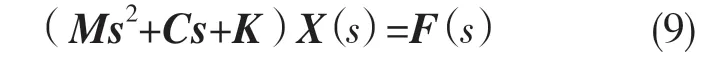
式中:X(s),F(s)——x 和f(t)的拉普拉斯变换。由式(9)可得
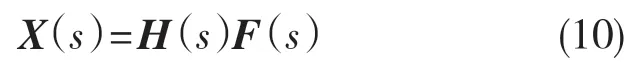
式(10)展开得

H(s)即为系统的传递函数矩阵,描述了系统对输入激励在频域中的传递特性。输入振动的各频率成分通过该系统时,系统对输入的一些频率成分进行响应放大,对其他一些频率成分响应衰减,从而使系统响应具有新的频率分布,这种动力特性由传递函数来定量表达[5]。
3 车架模态分析
本文研究的货车车架采用边梁式结构,初始结构设计由2 根纵梁和6 根横梁构成。车架联接形式为焊接,材料均选用16Mn,其材料参数如表1 所示。

表1 16Mn 材料参数Tab.1 16Mn material parameters
壳单元可以很好地模拟结构的弯扭和剪切变形,同时考虑到车架横纵梁的长度、宽度远大于厚度,本文采用壳单元进行车架有限元建模。车架初始结构如图1 所示。

图1 车架初始结构网格模型Fig.1 Initial structure mesh model of frame
车架约束简化后施加,参照文献[6]约束信息如表2 所示。

表2 车架结构约束信息Tab.2 Frame structure constraint information
Lanczos 法求得车架初始结构100 Hz 范围内模态,表3 列出了固有频率和对应的振型。
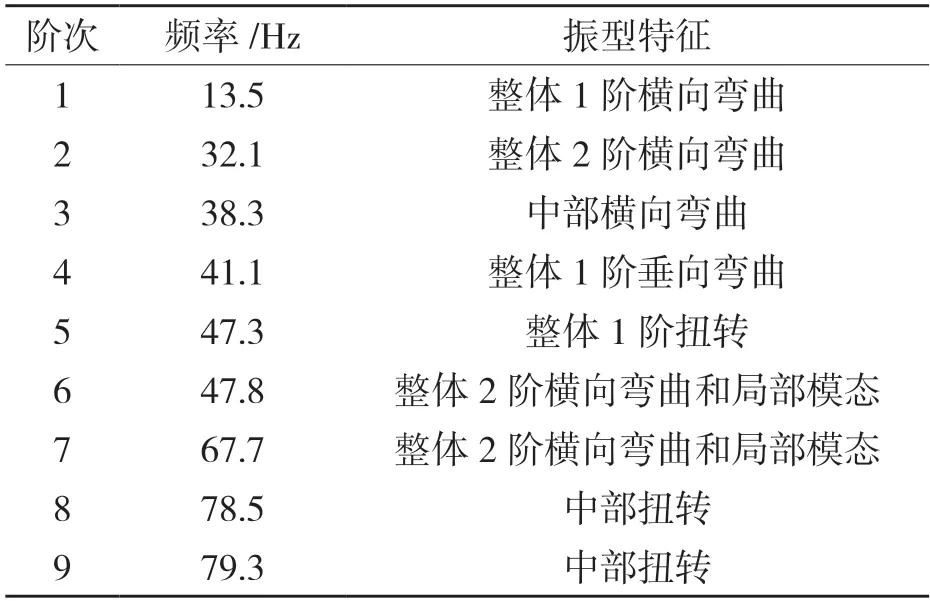
表3 车架初始结构模态分析Tab.3 Modal analysis of initial frame structure
图2— 图5 为车架结构前4 阶振型。

图2 1 阶横向弯曲Fig.2 First order transverse bending

图3 2 阶横向弯曲Fig.3 Second order transverse bending

图4 中部弯曲Fig.4 Middle bend

图5 1 阶垂向弯曲Fig.5 First order vertical bending
4 传递函数分析
本文研究的货车发动机为四缸四冲程发动机,根据式(12),可以计算发动机在怠速转速和正常行驶转速下的激励频率。

式中:z——发动机缸数;n——发动机转速,r/min;τ——发动机冲程数。
当怠速为 600~800 r/min,激振频率为20~26 Hz。最大功率转速为 2 600 r/min 时,发动机的激振频率为86 Hz;最大转矩转速为 1 300 r/min时,发动机激振频率为 43 Hz[7]。接近41.1 Hz 的第4 阶频率,发生共振的可能性很大。
车架第3、4 根横梁是发动机安装位置,为了在设计初期进一步了解发动机激励对货车装载货物的影响,考察了车架第3、4 根横梁处到车架后部纵梁的传递函数。计算初始频率为 2 Hz,频率增量为 2 Hz,频率增加 49 次,得到0~100 Hz 范围内的传递函数。激励点和响应点均为垂直于车架平面Z 方向。点的选取如图6 所示。
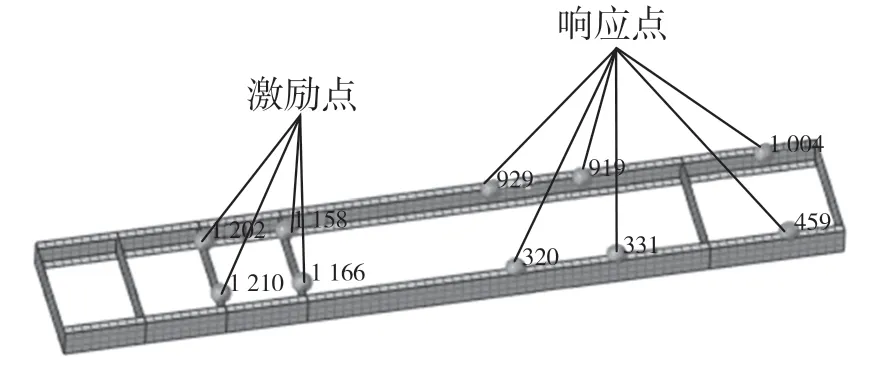
图6 激励点与响应点位置Fig.6 Location of excitation point and response point
图7 是在HyperWorks 中计算得到100 Hz 范围内的传递函数。
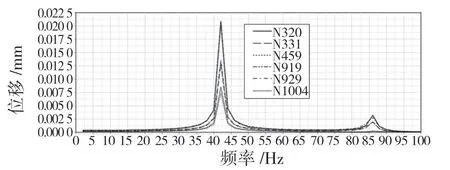
图7 车架初始结构传递函数曲线Fig.7 Transfer function curve of initial structure of frame
从图7 可以看出纵梁上选取的6 个响应点在频率42 Hz 振幅出现明显增大。对比模态结果,产生这么大振幅的原因是车架的第4 阶固有频率41.1 Hz对应的垂向弯曲振型与激振力方向相同。频率86 Hz 处存在较小的峰值,可能是中部扭转模态的影响。在车架固有频率与激励频率靠近处传递函数存在峰值。表4 列出了纵梁上6 个响应点的共振频率及幅值。

表4 纵梁响应点的振动幅值和频率Tab.4 Vibration amplitude and frequency of response point of longitudinal beam
综上所述,纵梁在激励频率为42 Hz 时,具有最大振动位移,且最大位移在节点320 和929处。同时考虑尽可能避免车架第3 阶中部弯曲模态,并结合实际需要,在初始结构中、后部增加2 根横梁以提高车架刚度。优化后车架网格模型如图8 所示。
图8 修改后车架网格模型Fig.8 Modified frame mesh model
对修改后的车架进行模态重分析,得到100 Hz范围内的7 阶固有频率和振型,如表5 所示。

表5 修改后车架模态分析Tab.5 Modal analysis of modified frame
优化后车架模态频率变化比较小,但100 Hz范围内固有频率从9 阶减少到7 阶,中部弯曲振型没有了。一阶垂向弯曲模态从41.1 Hz 下降到39.3 Hz,稍微远离了发动机激振频率。同时,从图9 车架优化后的传递函数曲线可以看出,响应点共振幅值从0.020 7 mm 下降到0.018 2mm,下降了0.002 5 mm,比优化前减少12%。且原传递函数曲线在频率86 Hz 处的峰值没有了,因为优化后车架在此频率附近没有振型变化。
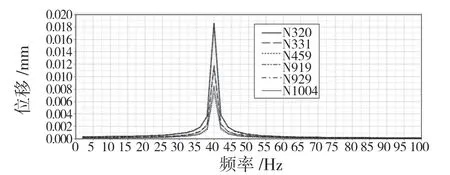
图9 车架优化后传递函数曲线Fig.9 Transfer function curve of frame after optimization
5 结论
(1)通过对车架初始结构的模态分析,车架中部存在明显弯曲振型,对货物承载不利;
(2)计算车架横梁发动机位置处到纵梁的传递函数,在频率42 Hz 处产生明显峰值,与车架第4 阶垂向弯曲模态相对应;
(3)为改善车架的中部刚度,结合实际需要,在车架中、后部增加2 根横梁。优化后车架的模态分析和传递函数计算相对比较理想,中部弯曲振型得到改善,共振处响应点峰值下降12%;
(4)把传递函数应用到模态分析中,为结构可能发生的振动做出预测。

