基于ANSYS 的机床床身尺寸优化设计
房久剑,李天箭
(200093 上海市 上海理工大学 机械工程学院)
0 引言
机床的优化设计方法有很多,美国 Catholic大学的 Bianchi G、Iowa 州立大学的Vance J M、ISU 研究中心的Yeh T P、Michigan 大学的 Jiang T和 Chiredast M 都分别提出了几种关于机床优化设计的方法:一是将控制技术和虚拟现实技术相结合;二是对零部件进行建模并拓扑优化的方法;三是利用有限元方法进行参数化设计[1-3]。本文通过以某一机床床身基础结构为模型进行有限元分析结构尺寸参数对最大相对变形和固有频率的影响,来确定某一最优的尺寸参数,进而来改进机床床身结构性能。
1 参数化三维建模
机床的零部件较多,但是对整机结构性能影响较大的零部件有机床床身、立柱、主轴箱以及工作台和滑鞍等,而本文主要是对机床床身进行结构性能的分析,因此对机床床身模型进行简化。在ANSYS Workbench 中的DM 模块建立机床床身三维模型,如图1 所示。简化的床身模型尺寸为:1 350 mm×900 mm×310 mm。
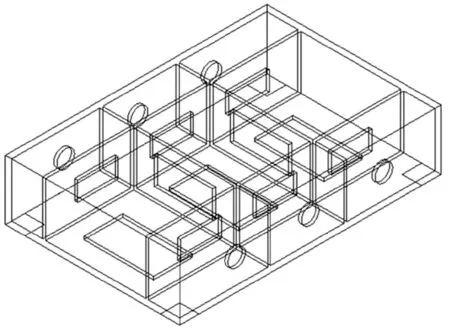
图1 DM 床身三维模型Fig.1 DM 3D bed model
根据秦大同、谢里阳主编的《现代机械设计手册》第1 卷第2 篇,零件结构设计中提及的灰铸件外壁厚、内壁厚设计尺寸,将原始的模型外壁、内部筋板厚度分别设为12 mm 和10 mm。
2 机床床身有限元分析
2.1 材料属性
机床床身的材料为灰铸铁,弹性模量E=1.1×1011Pa,材料密度ρ=7.2×103kg/m3,泊松比v=0.28。
2.2 网格划分
将机床床身的三维模型利用有限元网格划分成四面体单元模型,如图2 所示。网格总共包含92 187 个节点,46 401 个单元。

图2 四面体网格Fig.2 Tetrahedral mesh
2.3 载荷和约束
机床工作时,各个部件所受的力各不相同,机床床身所受到的力方向也各不相同。机床床身主要受主轴箱的自重、主轴箱刀具的径向力、工作台的自重以及横向的摩擦力、立柱的自重等,所以在机床床身上面简单地施加XYZ 方向各100 N 的均布载荷,底面四角固定,如图3 所示。

图3 载荷与约束Fig.3 Load and constrain
3 尺寸优化设计
3.1 优化数学模型的建立
结构优化设计中,设计变量为待确定的一些参数,这些参数反映了结构的形状大小、性能优劣等。在ANSYS Workbench 结构优化设计中所设定的设计变量不能多于60 个,各变量之间可以用数学表达式表示,简称参数耦合。设计变量通常用x1,...,xn表示,并构成一个向量[4],即

本文设计变量为外壁厚depth(x1)和内部筋板厚度rib(x2),即X=[x1,x2]T,单位:mm。选择导轨最大相对变形y1和1阶固有频率f0为多目标函数[5]。
约束条件:
考虑可铸造性的尺寸厚度的上下限约束,设置外壁尺寸为8~24 mm,筋板尺寸为6~22 mm。
综上,床身结构尺寸优化数学模型为
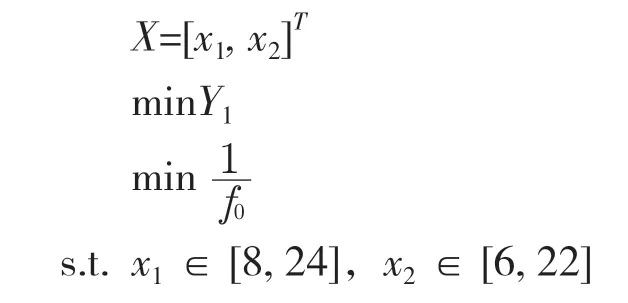
3.2 响应面分析
对设计变量参数进行设置,通过ANSYS Workbench 中Response Surface 模块对机床床身进行响应面分析,得出如图4、图5 所示的最大变形和1 阶固有频率的响应面分析结果,图6 所示为各参数变量对机床床身最大变形、最大应力和1 阶固有频率的灵敏度分析[6]结果。
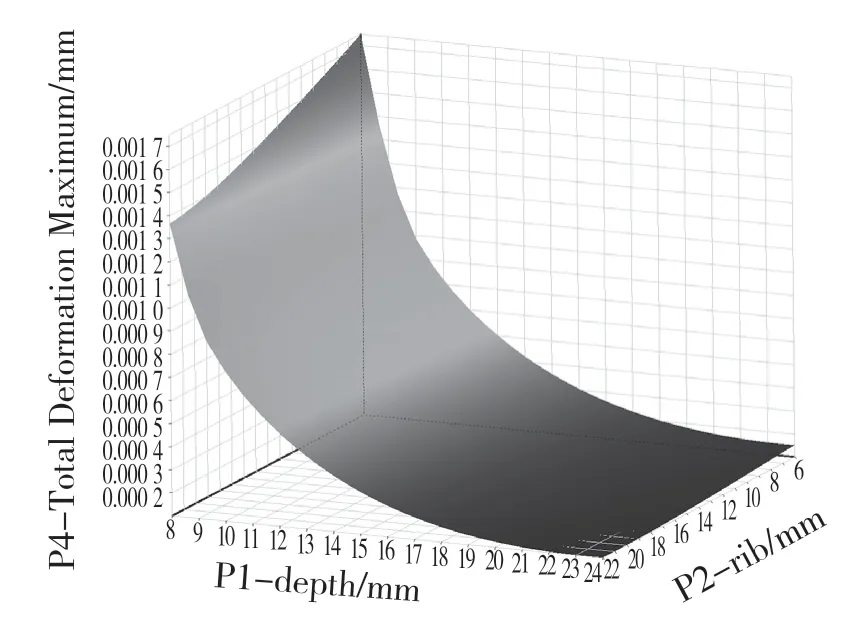
图4 最大相对变形Fig.4 Maximum relative deformation
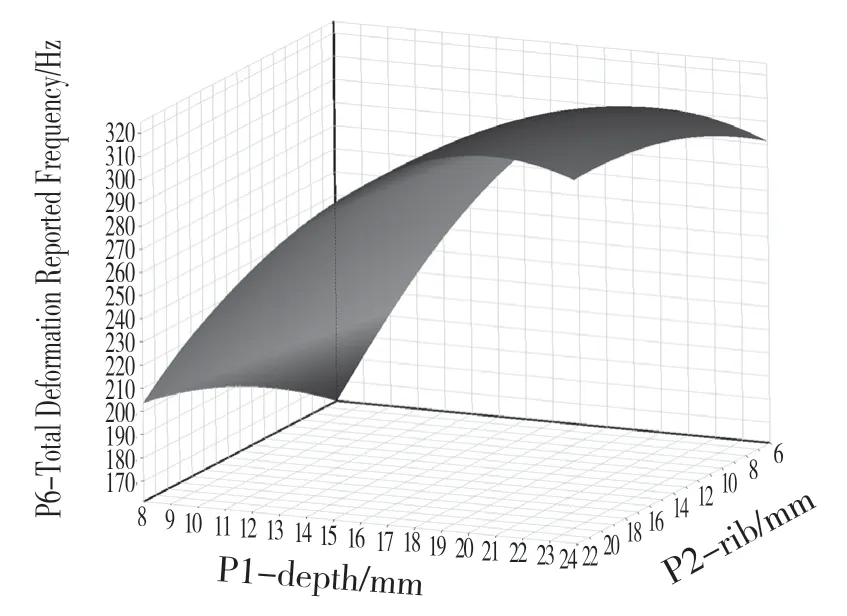
图5 1 阶固有频率Fig.5 First order natural frequency
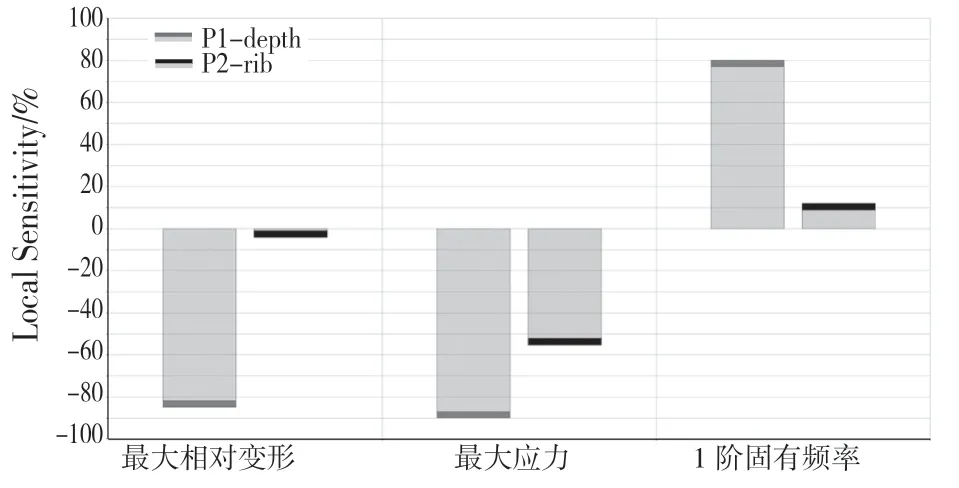
图6 灵敏度分析Fig.6 Sensitivity analysis
通过外壁厚度depth 和筋板厚度rib 对最大应力、最大相对变形和一阶固有频率的响应面分析和灵敏度分析,可以得出外壁厚度和筋板厚度对结构动静态性能(应力、变形和一阶固有频率)都有影响,其中外壁厚度变化对结构动静态性能的影响高于筋板厚度变化对结构动静态性能的影响。且随着外壁厚度和筋板厚度的增加,机床床身的最大相对变形随之减小,1 阶固有频率随之增加。
3.3 优化分析
利用ANSYS Workbench 优化模块对机床床身尺寸进行优化,得如图7 所示3 组候选点(最优解)以及静态分析的最大相对变形迭代过程(图8)和模态分析的1 阶固有频率迭代过程(如图9)。可得最优解为外壁厚度depth=21.372 mm,筋板厚度rib=20.218 mm。考虑到实际铸造工艺,将最优解近似等效为21 mm 和20 mm。
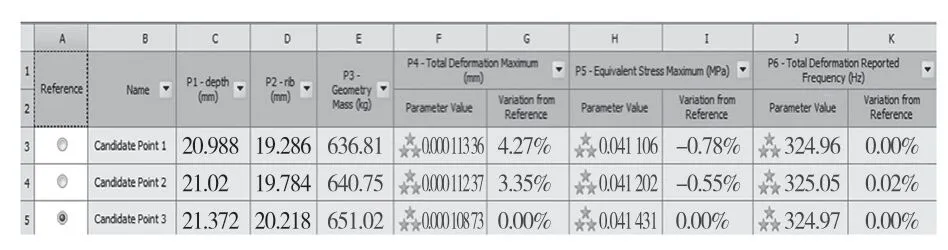
图7 优化后的候选点Fig.7 Optimized candidate points
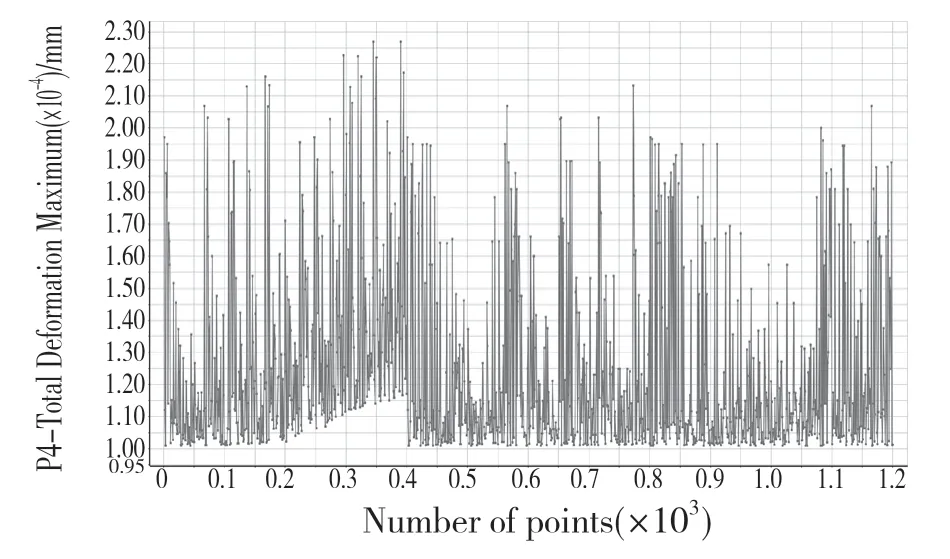
图8 最大相对变形迭代Fig.8 Maximum relative deformation iteration

图9 1 阶固有频率迭代Fig.9 First natural frequency iteration
对此机床床身进行静力学分析和模态分析[7-8],得到如图10—图13 所示的结果,将数据结果统计成表1 所示。
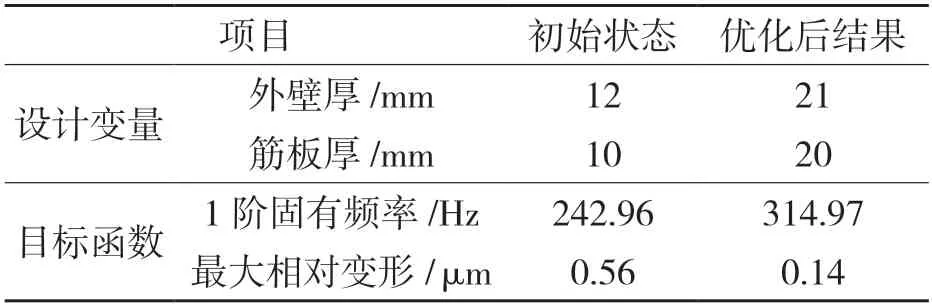
表1 优化前后对比Tab.1 Comparison before and after optimization

图10 优化前最大变形Fig.10 Maximum deformation before optimization

图11 优化后最大变形Fig.11 Maximum deformation after optimization

图12 优化前1 阶固有频率Fig.12 First natural frequency before optimization

图13 优化后1 阶固有频率Fig.13 First natural frequency after optimization
对比优化后尺寸(外壁厚度21 mm,筋板厚度20 mm)与优化前尺寸(外壁厚度12 mm筋板厚度10 mm)的各结果可知,优化后机床床身最大相对变形由0.56 降至0.14,大大提升了机床床身的静态性能。1 阶固有频率由242.96 Hz提升至314.97 Hz,提升了29.6%,大大提升了机床床身的动态性能,从而实现了机床床身的尺寸优化设计过程,对机床整体的性能提升有所帮助。
优化前后,机床床身的前6 阶固有频率的对比折线图如图14 所示。从图14 可以直观地看出,优化后的床身尺寸结构的各阶频率都高于优化前对应的各阶频率。这也证实了前面所述的优化后床身尺寸,可以提升机床床身的动静态性能。

图14 前6 阶固有频率对比Fig.14 Comparison of the first six natural frequencies
4 结论
(1)本文针对机床床身不同尺寸对其结构性能的影响,对机床床身进行了结构设计,得出最优的机床床身尺寸结构优化设计方案。通过响应面分析、优化分析,可以得出机床床身的外壁厚度和筋板厚度对机床床身结构性能都有一定的影响,且外壁厚度对其影响更为显著。
(2)通过比较优化前后的最大相对变形和其前六阶固有频率,得出优化后的尺寸参数可以使机床床身结构性能达到最优。
(3)机床床身尺寸结构优化的方法同样适用于优化立柱和主轴箱等重要的机床零部件,为机床整体优化提供了参考。

