带间隙的埋刮板输送机链传动接触动力学

肖亚茹,邵战涛，王明明，琚立颖

(1.华北理工大学 机械工程学院，河北 唐山 063210；2.住重中骏(厦门)建机有限公司，福建 厦门 361012)

链轮之所以能够带动链条运动主要依靠动力设备把扭矩传输给链轮，链轮带动链条旋转。链条主要包括套筒、滚子、销轴和内外链板等四部分，为了保证链传动系统的稳定运行滚子与套筒之间会留有间隙。由于间隙的存在，使得面面接触变为线接触或者点接触，系统载荷传递受到影响，加剧了滚子和套筒的磨损和破坏。特别在环境恶劣、载荷复杂的工作环境下，理想模型在间隙铰的存在的情况下不再适用，使系统表现出明显的非线性特性。间隙不仅造成了系统的理想运动和实际运动之间的偏差，而且使铰接处或零件间不断的发生碰撞和冲击加剧了系统的磨损和失效。

国内外有部分学者对含间隙的链传动系统动力学进行了分析。2010年，Lixin X U对建立间隙的链传动系统的简化模型进行分析，建立了基于牛顿定律的系统的运动方程。应用龙格-库塔法求解非线性微分方程[1]。2015年，Pereira C 考虑了滚子与衬套之间的间隙，建立了整个的链传动系统仿真模型。对恢复系数、摩擦系数和链条预紧的不同组合，得到链传动的动态响应[2]。2009年，吉林大学的冯增铭等人提出了套筒与和销轴之间存在间隙的问题，在RecurDyn建立了含有间隙的链系统仿真模型，对链轮和链条的接触动态特性加以分析，获得了链轮、销轴和链板的接触力[3]。

然而通过以上方法对含间隙的链传动系统进行分析有一定的局限性，没有考虑在接触碰撞过程的能量损失。用Lankarani—Nikravesh连续接触力模型计算法向接触力，改进的库伦摩擦模型计算切向摩擦力，应用到拉格朗日方程，用龙格—库塔法进行求解，得出不同间隙下链传动系统的动态特性。

1链节铰链间隙模型

1.1 接触碰撞力模型

间隙系统的典型现象是接触冲击，因此接触力模型的选择对分析间隙对系统动态特性的影响，使结果更接近实际是非常重要的。先前学者们使用Hertz接触力模型[4]，但是该模型忽略了接触碰撞过程耗散掉的能量，因而不能准确的反映接触碰撞造成的能量损失。随后，众多知名人士对含有间隙的接触碰撞现象进行了深入研究，主要包括Kelvin-Voig模型[5]，Freudenstein和Dubowsky的非线性弹簧阻尼模型[6]，Crossley和Hunt的非线性弹簧阻尼模型[7]。Lankarani和Nikravesh[8]把Crossley和Hunt理论不断深化，依据Hertz接触理论提出了非线性弹簧阻尼模型，并且考虑了恢复系数和碰撞过程的阻尼因素。

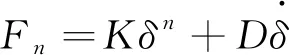
(1)

D=ηδn

(2)

式中：

D—碰撞过程的阻尼系数；

η—粘滞阻尼因子。

式中其他参数的意义同上。

应用冲击前后动力学进行分析，能量损耗可用恢复系数和相对速度法来计算：

(3)

(4)

式中：

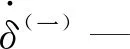
ce—恢复系数；

m(eff)—当量质量，kg；

mi、mj—滚子和套筒的质量，kg。

能量损失也可以通过在迟滞回线周围的接触力的积分来表示，具体表达式为：

(5)

结合式(3)和(5)，可以得到：

(6)

因此得到阻尼系数D的表达式为：

(7)

因此方程(1)可写成：

(8)

Lankarani和Nikravesh提出的连续接触力行为不仅考虑了碰撞过程引起的能量损失，而且包含了碰撞物体材料特性、变形深度、碰撞速度等信息，因此对含有间隙系统做动态啮合特性分析时被国内外学者广泛应用。

1.2 切向摩擦力模型

间隙运动副的切向摩擦力采用Coulomb摩擦力模型，为了能准确描述切向摩擦力采用修正后的Coulomb摩擦力模型，该模型中存在修正系数cd，摩擦力是切向滑动速度的函数，它与切向滑动速度有关，其曲线图见图1，切向摩擦力表达式为：

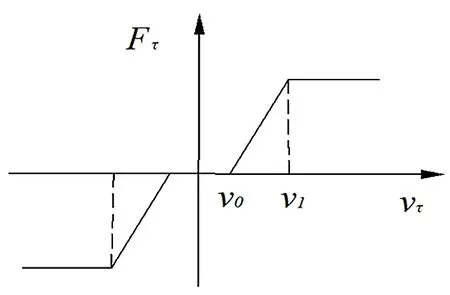
图1 摩擦力与速度的关系

(9)

(10)

式中：

vτ—相对切向速度，m/s；

cf—摩擦系数；

cd—动态修正系数；

v0、v1—切向速度的给定范围，m/s。

链节张力是法向接触力与切向摩擦力的矢量和，所以链节张力表示成：

Fi=Fn+F

(11)

链节间的张力大小为：

(12)

结合式(8)和式(9)得

(13)

另上式中

(14)

(15)

2动力学方程的建立

2.1 正常工况下动力学方程的建立

建立完整链传动模型示意图见图2，把XOY坐标系建立在主动链轮中心，设xi、yi为链节i在x、y方向广义坐标。

图2 链传动系统模型

在链轮链条初始时刻，假设主从动链轮上和链条紧边中第一个滚子r1、rp开始啮合的方位角为θ1和θ2，则当整个系统转动时，与主从动链轮上滚子r1、rp相对应的轮齿位置角为

θs1=θ1+φ1

(16)

θp1=θ2+φ2

(17)

式中：

φ1、φ2—主从动链轮转角，度。

在上面研究的基础上，主从动链轮上任何滚子ri相应的轮齿位置角能够写成：

(18)

(19)

式中：

z1、z2—主从动链轮齿数。

本文采用拉格朗日方程来建立整个系统动态特性方程，第一步先计算出传动模型的动能、势能、耗散能和广义力[9]。

2.1.1系统动能

(1)链节动能

(20)

式中：

N—链节总数。

(2)主动链轮扭转动能

(21)

式中：

I1—主动链轮转动惯量，kg·m2。

(3)从动链轮扭转动能

(22)

式中：

I2—从动链轮转动惯量，kg·m2。

2.1.2系统势能

(1)链节拉伸弹性变形势能和重力势能

(23)

式中：

RB—滚子半径，m；

RJ—套筒半径，m。

(2)主动链轮与链节接触弹性变形势能

(24)

式中：

kc—滚子与链轮接触刚度，N·m-1；

Rt—齿廓半径，m。

(3)从动链轮与链节接触弹性变形势能

(25)

式中：

a—链系统中心距，m。

2.1.3系统耗散能

(1)链节拉伸阻尼耗散能

(26)

(2)主动链轮和链节接触阻尼耗散能

(27)

式中：

cc—滚子与链轮接触阻尼，N·s·m-1。

(3)从动链轮和链节接触阻尼耗散能

(28)

系统的广义力是主从动链轮产生的法向惯性力fsn、fpn与切向惯性力fst、fpt的组合，即：

(29)

(30)

(31)

(32)

(33)

(34)

式中：

mi—链节质量，kg；

Rs1、Rs2—主从动链轮分度圆半径，m；

将以上能量表达式和广义力应用到拉格朗日方程：

(35)

式中：

qi—广义坐标；

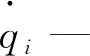
Qi—广义力。

将式(20)～(34)带入到式(35)中建立整个机构的啮合动态方程：

(36)

(37)

2.2 啃齿和跳齿工况下动力学方程建立

通过前面第三章啃齿和跳齿的机理可以看出，啃齿和跳齿的主要原因是链条节距的缩短和变长，使图2所示的链传动系统模型的θsi发生变化，因此为了更好的模拟啃齿和跳齿工况给定一个参数Δθ修正θsi。

啃齿工况下：

(38)

跳齿工况下：

(39)

3求解方法及基本参数确定

采用四阶龙格—库塔法计算方程，得出了在正常、啃齿和跳齿工况下不同间隙下接触力、速度和加速度曲线图。具体参数如表1所示。

表1 链传动系统结构和几何参数

4动力学分析

4.1 正常工况下动力学分析

将表1中的参数值带入(36)式中，通过四阶龙格—库塔法，得出间隙c取不同数值时，对链传动系统的接触力、速度以及加速度的影响，如图3～图5所示。

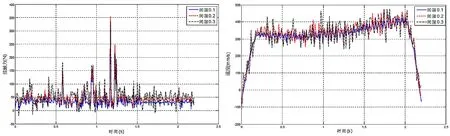
图3 不同间隙下接触力关系 图4 不同间隙下速度曲线图

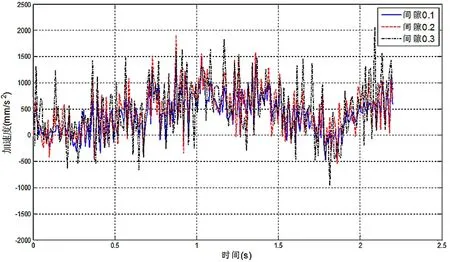
图5 不同间隙下加速度曲线图

由图3～图5可得，在1.2 s左右接触力达到最大，说明此刻冲击振动明显，这主要受到链传动系统多边形效应的影响，尤其是啮合冲击作用的影响。在链条啮出从动链轮时，速度逐渐增大，当进入紧边后速度趋于平稳并伴有不同幅度的波动，当链节进入到主动链轮速度逐渐减小。链条速度的这种波动也受到链轮六边形效应的影响。在链条与链轮啮合的过程中加速度先增大后减小。由图容易得知随着间隙的扩大，无论是接触力、速度、加速度的峰值还是波动幅度都随之增大。

4.2 啃齿工况下动力学分析

将等式(38)代入到等式(36)和(37)得出啃齿工况动态特性曲线图。图6、图7分别为在啃齿工况间隙下取不同值时接触力、速度随时间的变化曲线图。

图6 不同间隙下接触力关系 图7 不同间隙下速度曲线图

图8为啃齿工况间隙下取不同值时加速度随时间的变化曲线图。

图8 不同间隙下加速度曲线图

由图6～图8不难看出，发生啃齿时在链轮与链节啮合过程中在1.2 s时接触力达到最大且峰值比正常工况大，说明此刻冲击明显；速度与加速度波动幅度明显增大，且峰值也比正常工况偏大。并且随着间隙增大，波动明显。

4.3 跳齿工况下动力学分析

图9～图11描绘了在跳齿工况间隙取不同值时接触力、速度以及加速度随时间的变化曲线图。

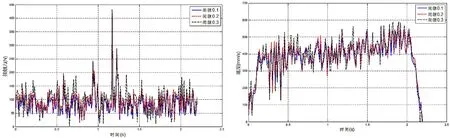
图9 不同间隙下接触力关系 图10 不同间隙下速度曲线图

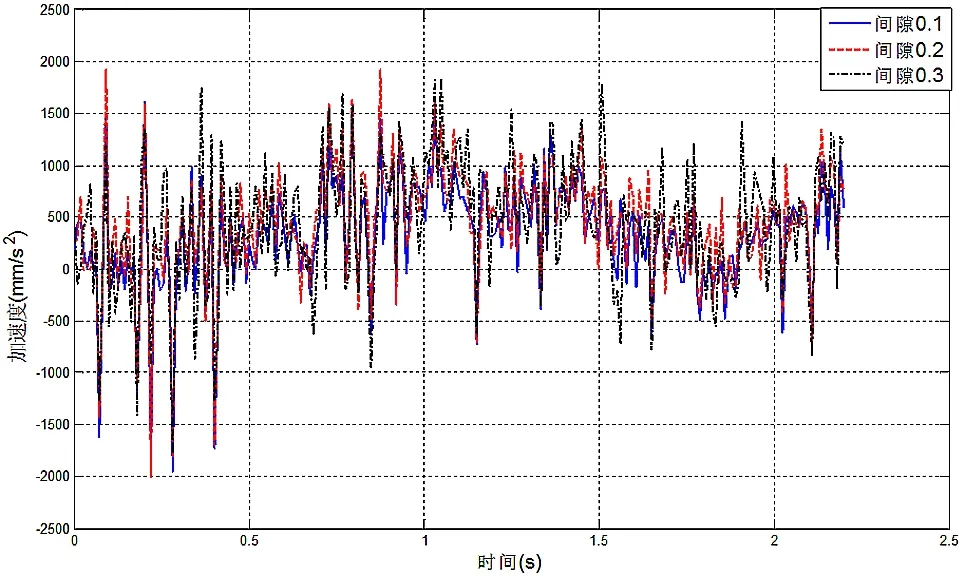
图11 不同间隙下加速度曲线图

由图9～图11得出在跳齿工况下，接触力在1.2s时达到最大且峰值大于正常工况说明此刻冲击作用较为明显；开始接触时速度波动明显，加速度向相反方向波动，且啮合时的峰值比正常工况偏大，接触力、速度、加速度都因间隙尺寸的变大而变大。不难看出无论是啃齿还是跳齿三者的峰值都比正常工况大，因此会加快链轮链条的磨损。

5结论

(1)正常工况和啃齿和跳齿工况相比，无论是接触力、速度还是加速度变化曲线比较平稳。且受到多边形效应的影响，接触力在大约1.2s的时间内达到最大，说明此刻冲击作用较为明显；

(2)正常工况、啃齿和跳齿工况下，无论是接触力、速度还是加速度大小都随间隙尺寸的增大而增大。啃齿和跳齿工况下，开始接触时接触力、速度及加速度波动幅度较大，且峰值比正常工况偏大，因此在设计与制造时应避免产生过大的间隙，间隙过大会加速链传动系统的磨损。