后房压力变化对虹膜变形的流固耦合有限元分析

曹月红 蔡建程 陈雁翎 Volodymyr Brazhenko Ievgen Mochalin

青光眼是全球第一位不可逆性致盲眼病。据预计，2020 年全世界青光眼患者将达到7 960 万，其中原发性闭角型青光眼（PACG）患者占26%[1]。房角关闭的发病机制中虹膜-晶状体间隙变化引起房水由后房流向前房的阻力随着相对性瞳孔阻滞的进展而增加，致使前后房压力差增大，周边虹膜向前膨隆，堵塞小梁网的滤过部分，最终导致眼压升高。急性闭角型青光眼早期有效的干预措施可以挽救患者的视功能[2]。医学临床观察及定性分析PACG房角关闭机制已有一些文献报道[3-6]，而定量分析虹膜变形及房角关闭的文献相对较少。房水流动以及虹膜在房水作用下的变形定量分析，对于深入了解闭角型青光眼的发病机理、预防以及治疗是非常重要的。

随着计算流体动力学（Computational fluid dynamics，CFD）的发展，数值求解眼内复杂流动越来越流行。Heys和Barocas[7]计算温差驱动自然对流情况下人眼内房水流动并解释Krukenberg条纹形成的机理。郭竞敏等[8]基于房水生理学相关理论及流体力学基本原理，对不同宽窄的前房进行三维重建，并对不同瞳孔直径及体位的房水流动进行数值模拟。陈伟等[9]根据房水生理学基本理论，在超声生物显微镜扫描结果的基础上构建了以人眼前房为主的二维模型，计算结果表明虹膜膨隆较为严重时，前后房的眼压差值急剧上升。Wang等[10]数值研究了3D打印人眼模型在房水流场作用下的虹膜结构模型，并用粒子图像测速（Particle image velocimetry，PIV）技术进行了实验验证，表明重力方向和温度对房水流动影响很大，从而影响虹膜的变形。

在虹膜变形研究方面，陈琛等[11]对实验动物的虹膜进行整体加压，研究瞳孔阻滞力作用下的虹膜面应变同曲率半径的变化与前后房眼压强差（后文简称前后房压差）的关系以及不同大小的瞳孔阻滞力与前后房眼压强差的关系。薄雪峰等[12，13]设计模拟了瞳孔阻滞及虹膜膨隆的实验系统和方法，并对兔眼虹膜在不同前后房压差产生的膨隆变形及房角开放度进行研究，研究结果与临床观察相一致。张向东等[14]依据力学原理建立了虹膜应变与前后房压差之间的函数关系，分析虹膜膨隆过程中虹膜变形与前后房压差之间的定量关系。

笔者数值研究正常虹膜-晶状体间隙（30 μm）及虹膜几乎粘连（虹膜-晶状体间隙分别为2 μm、5 μm）情况下的房水流动以及房水压力作用下的虹膜变形，房水流动计算由CFD得到，并基于单向流固耦合技术，进行虹膜在流场作用力下变形的有限元分析。严格来讲房水与虹膜之间耦合为双向耦合，虹膜在房水压力作用下变形，虹膜的变形反过来影响房水流动。本研究先计算虹膜在房水压力作用下变形，其目的是通过定量分析虹膜-晶状体间隙对前后房压差及虹膜变形的影响，为PACG瞳孔阻滞发病机制的探索提供参考。

1 数学模型

1.1 房水流动

与血液不同，房水可以建模为Newton流体，所以其流动受控于Navier-Stokes方程[15]。同时由于流速很小（最大流速在mm/s量级），所以可视为不可压缩流动，其定常流动的连续方程及动量方程为：

式中v为速度，ρ、p、μ为流体密度、压力及动力黏度，g为重力加速度矢量。

由于温度梯度的存在，流体密度发生变化，产生浮力，形成自然对流。密度变化与Boussinesq假设近似[16]：

式中ρ0为参考密度、β为体积膨胀系数，T和Tref分别是温度和参考温度。

对于不可压缩流动，忽略黏性引起的耗散项后，描述稳态温度场的方程为：

其中cP为定压比热容，κ为热传导系数。房水的特性见表1。

表1.房水物性[7]Table 1.Properties of aqueous humor used in simulations

判断房水流动的流态（层流或湍流），需使用特征Reynolds数和Rayleigh数：

D代表特征尺寸，如前房径向尺寸（10-2米量级），ν为特征速度，最大在10-3m/s量级。本研究的流场的温度△T=3 ℃，估算出Re～20<<2 300，Ra～50<<109，所以可以判断房水流动为层流流动。

前房房角出口为小梁网，本研究建模中使用了0.1 mm厚度的各向同性多孔介质区域代表一部分小梁网，并把其内的压力梯度表示为黏性损失项（Darcy定理）和惯性损失项：

式中α为渗透率，C2为惯性阻力系数。它们分别由下面公式[17]估计：

其中Dp是多孔介质填料床的平均粒径，它与孔径d之间的关系可以由Dp=d表示；ε为空隙率，定义为空隙体积除以填充床体积。

1.2 虹膜变形

虹膜结构材料为超弹性材料，学者们对其进行了测量研究，得出的结果有一定差异特别是在大变形情况下[11，14，18-20]。当虹膜变形较小，虹膜结构建模成线弹性体，参见文献[10，21]。对于线弹性体，用位移u表示的变形微分方程为：

式中E和ν分别为杨氏模量和泊松比，对于虹膜E=0.027 MPa，ν=0.49[10，21]；f为体积力，在本研究f=ρirisg，虹膜密度ρiris=1 050 kg/m3[22]。

其边界条件为虹膜根部固定（Dirichlet条件），即

而其他表面为应力边界条件（Neumann条件），即

由线弹线体的本构关系得到应力边界条件：

本研究使用有限体积法对房水流动进行计算，使用有限元法进行虹膜变形的计算。

2 数值计算模型

2.1 房水CFD模型

本研究的房水流道几何模型参考了文献[7，9]中的模型。图1显示了房水流动的模型，其中图1A图为正常虹膜形状，虹膜-晶状体间隙为30 μm。文献[7] 认为10 μm基本上为正常虹膜-晶状体间隙的最 小值，本研究在处理虹膜几乎后粘连的情况，分别设置虹膜-晶状体间隙为5 μm及2 μm，见图1B和C。图1中眼角膜的曲率半径为8.3 mm，晶状体曲率半径为10 mm，在眼中心轴上晶状体到角膜的距离为3 mm。后房直径为12.8 mm，瞳孔直径为3 mm。图1C中虹膜的瞳孔端部形状与图1A和B稍不一样，端部曲率半径从0.2 mm增加至0.29 mm，这主要为下文网格生成考虑。当虹膜-晶状体间隙为2 μm时，对较小曲率虹膜瞳孔端部进行结构化网格划分具有困难。

使用结构化六面体网格进行区域离散。六面体网格的优点是正交性好，离散误差比四面体网格离散误差要小，且同样大小使用网格量少。虹膜-晶状体间隙处使用11 层网格，以便更好地捕捉该处房水详细流场特别是物理量的梯度。图2显示了房水流动CFD模型，图中虹膜-晶状体间隙为图1B中的5 μm。计算模型共计使用约194万个单元，文献[17]的研究表明30 万六面体网格已经可以达到房水流动仿真的网格无关性要求。事实上眼内房水流动为层流流动，所以网格精细要求程度比湍流流动低。

图1.房水流动计算区域虹膜-晶状体间隙为30 μm (A)、5 μm (B)和2 μm (C)Figure 1.The computational domain of aqueous humor flow.The iris-lens gap is 30 μm (A),5 μm (B) and 2 μm (C).

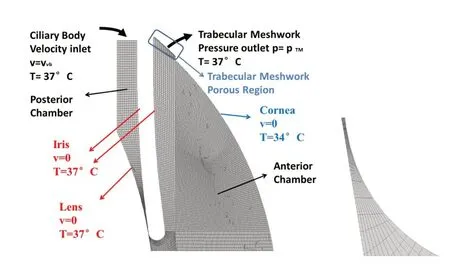
图2.房水流动动力的计算模型Figure 2.The computational model of aqueous humor flow.

前房房角出口位置设置厚度为0.1 mm的多孔介质区域，代表小梁网的一小部分。完整小梁网分为3 个部分：与前房相接的为葡萄膜网，然后靠外侧是角巩膜网，占小梁网大部分，最后是连接Schlemm管的邻管区薄层组织[23]。前2个区域小梁网组织孔径较大，约为100 μm，而邻管区组织孔径 为0.6 μm，小梁网空隙率ε≈0.5。本研究取孔径d=1 μm，空隙率ε≈0.5 作为多孔介质区域的参数，代表小梁网一小部分区域。该区域网格层数为11层。如果不设置该多孔计算区域，在房角出口处使用压力出口边界，计算时会遇到倒流现象，影响计算精度。

房水进口设为速度进口条件，进口速度由房水分泌量2.4 μm/min除以进口面积得到，进口处房水温度设为37℃。出口设置为压力出口，设置压力为15 mmHg，即1 995 Pa。壁面设置为无滑移壁面，角膜壁面温度设置为34℃，其余壁面温度设为37℃。温差引起自然对流为前房流动的主要原因。重力加速度为y方向。

在通用CFD软件ANSYS FLUENT中，采用有限体积法对房水流动的偏微分方程进行离散：动量方程和能量方程离散采用二阶迎风格式，压力速度耦合迭代采用SIMPLE算法[24]。迭代计算时，监测房水的体积平均压力及速度。迭代3 000 步以后，平均压力和速度均趋于常数，表明迭代趋于收敛，再继续迭代5 000步结束。

2.2 虹膜变形FEA模型

在ANSYS结构分析模块使用Solid186 单元进行虹膜结构的网格划分，共使用了134 080 个单元607 040个节点。Solid186为三维固体结构单元，具有二次位移模式，单元通过20个节点来定义，每个节点有3个沿着xyz方向平动自由度。图3显示了虹膜有限元网格。

虹膜根部设为固支约束，即设置该表面上节点xyz方向的位移为0；对于虹膜瞳孔靠近晶状体侧的边线分别设为自由及约束2 种情况，见图3。在其余表面上，使用表面效应单元Surf154从房水压力场插值得到对应单元表面的压力数据，使用ANSYS中的sfe命令进行表面载荷施加。然后进行虹膜结构变形及应力分析。有限元代数方程组的求解使用预处理共轭梯度（Preconditioned conjugate gradient，PCG）求解器。

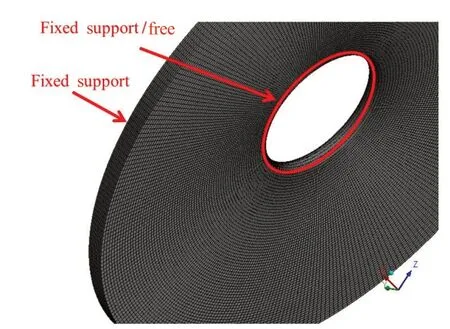
图3.虹膜有限元网格分析Figure 3.Finite element analysis mesh of the iris.

3 结果

3.1 房水流场

图4.房水速度场(mm/s)虹膜-晶状体间隙为30 μm（A）、5 μm（B）和2 μm（C）Figure 4.The intraocular velocity fields.The iris-lens gap is 30 μm (A),5 μm (B) and 2 μm (C).

在模型z方向作中截面（xy平面），其速度大小云图分布见图4。可以看到后房的流速非常小，在μm/s的量级；在虹膜-晶状体间隙处速度增加，此处为压差驱动的Poiseuille流动；前房房水呈整体的自然对流流动：瞳孔附近的房水温度较角膜壁面的高，由Boussinesq近似可知房水会因密度减小而形成浮力，到达上部房角时由于小梁网处的流动阻力较大，绝大部分房水拐弯流到角膜侧，并受冷后下沉，然后在下部虹膜侧受热后又上升，形成温差驱动的自然对流。整体上，房水流动的最大速度在mm/s量级，并且房角下部流出去的房水比上部的多。该房水流动模式与文献[7，8，25]的结果相似，表明本研究房水流动模型的正确性。

眼内压力分布如图5所示，可以看出对于正常虹膜形状，前后房压力几乎相等（后房平均压力比前房高0.476 Pa），而主要压力降发生在房角出口的小梁网（多孔介质区域）处。虹膜-晶状体间隙为 5 μm 时，后房压力比前房压力高31 Pa。对于2 μm的虹膜-晶状体间隙，前后房的压力差达到815 Pa。利用非线性乘幂函数对前后房压差与虹膜-晶状体间隙之间关系进行拟合，得到的函数见图6。从图中可以发现当虹膜-晶状体间隙小于 5 μm后，前后房压差开始迅速增加。

3.2 虹膜变形

把前后房的压力加载到虹膜表面上，先进行瞳孔无后粘连时的有限元分析，得到的虹膜变形结果如图7 所示，图中为从后房侧观察到的变形分布，黑色线框为变形前虹膜位置。从图7A中可以看出对于正常虹膜形状，虹膜在房水压力作用下的变形是非常小的，最大位移发生在瞳孔附近，其值为51.2 μm，变形方向主要为从后房向前房。

图5.房水压力场（Pa）虹膜-晶状体间隙为30 μm（A）、5 μm（B）和2 μm（C）Figure 5.The intraocular pressure fields.The iris-lens gap is 30 μm (A),5 μm (B) and 2 μm (C).

图6.前后房压差与虹膜-晶状体间隙的关系Figure 6.The relationship between the anterior and posterior chamber pressure difference and the iris-lens gap.CFD,computational fluid dynamics.

对于瞳孔几乎后粘连（虹膜-晶状体间隙为5 μm和2 μm）的情况，虹膜变形分布见图7B和C，可以看出在后房较大压力作用下，虹膜整体脱开晶状体侧向前房变形，对于5 μm虹膜-晶状体间隙，虹膜的最大变形量达到2.597 mm，而对于2 μm虹膜-晶状体间隙，其最大变形量达到7.479 cm，这在实际中显然是不可能的。这是因为本研究的计算使用流固单向耦合，即只计算房水压力作用下的虹膜变形，而事实上房水与虹膜的互相作用是动态的，当虹膜离开晶状体一定距离时前后房压差会减小，从而虹膜的变形量会减小。这一动态过程的模型需要双向耦合，一般使用顺序耦合方法计算，如沈双等[26]进行人内耳前庭系统膜迷路的流固耦合数值模拟时就使用了该方法。

图7.虹膜瞳孔无后粘连时的变形 虹膜-晶状体间隙为30 μm（A）、5 μm（B）和2 μm（C）Figure 7.The iris deformation when it is free at the pupil boundary.The iris-lens gap is 30 μm (A),5 μm (B) and 2 μm (C).

图8.虹膜瞳孔后粘连时的变形虹膜-晶状体间隙为30 μm（A）、5 μm（B）和2 μm（C）Figure 8.The iris deformation when it is fixed at the pupil boundary.The iris-lens gap is 30 μm (A),5 μm (B) and 2 μm (C).

下面计算假设瞳孔后粘连，从而在虹膜有限元模型中把后房侧虹膜瞳孔一周的节点自由度约束为0，如图3所示。分析得到的虹膜变形结果如图8所示，可以看出在30 μm的虹膜-晶状体间隙的前后房压差作用下，虹膜的变形量非常小，在微米量级。而在5 μm虹膜-晶状体间隙的前后房压差作用下，虹膜已经有明显的膨隆，虹膜中间部位的最大变形量已经达到了0.342 mm。而在极端的2 μm虹膜-晶状体间隙时，虹膜膨隆程度已经超过常规前房深度（2.5～3.0 mm）。

对以上情况的虹膜最大变形量与虹膜-晶状体间隙之间关系进行乘幂函数非线性拟合，得到结果见图9。同样可以发现当虹膜-晶状体间隙小于5 μm 后，虹膜膨隆程度将加速。如果认为虹膜平面距离角膜约为2 mm，如图1C中所示，那么从图9 可以看出当虹膜-晶状体间隙在3 μm时，虹膜最大变形量已经超过了2 mm，此时虹膜将与角膜接触，阻碍房水从前房角排出，从而引发闭角型青光眼。所以可以定量认为3 μm虹膜-晶状体间隙是后房眼压升高及前房角关闭的指导参数。

4 讨论

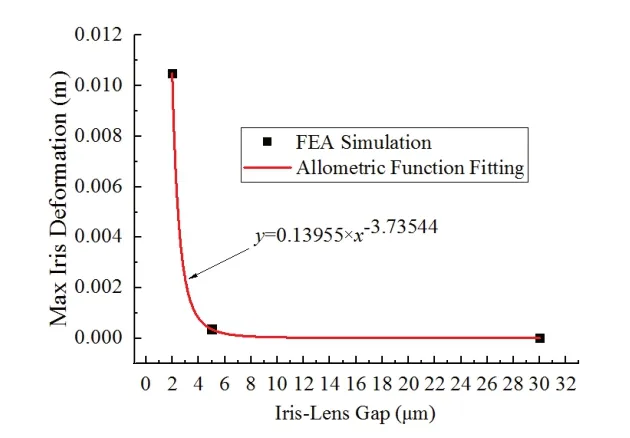
图9.虹膜最大变形与虹膜-晶状体间隙的关系Figure 9.The relationship of the maximum iris deformation with the iris-lens gap.

临床上认为瞳孔阻滞是PACG发作的一种重要机理，由于虹膜-晶状体位置不当引起房水由后房流向前房的阻力随着瞳孔阻滞的发展而增加，致使前后房压力差增大，虹膜向前膨隆并与角膜接触，致使房角关闭，最终导致眼压升高。对于这一机理的定量分析研究目前尚不多，本研究正是在这一背景下，利用CFD数值计算了虹膜-晶状体间隙分别为30 μm、5 μm、2 μm情况下的房水流动，基于单向流固耦合把房水压力施加到虹膜表面上，利用有限元分析计算了虹膜变形，以研究瞳孔阻滞引发的闭角型青光眼。

流场的分析表明，对于30 μm正常虹膜-晶状体间隙，前后房的压力几乎相等；对于5 μm和2 μm虹膜-晶状体间隙（瞳孔几乎后粘连），后房比前房压力高出30 Pa和810 Pa。后房的流速很小（量级为μm/s），虹膜-晶状体间隙的流动为压差驱动的Poiseuille流动，而前房流动主要为温差驱动的自然对流，最大流速在mm/s量级。利用乘幂函数对前后房压差与虹膜-晶状体间隙之间关系进行非线性拟合，发现当该间隙小于5 μm后，前后房压差将异速增加。

虹膜变形的有限元分析结果表明，在瞳孔无后粘连时，在较大的后房压力作用下虹膜脱开晶状体向前房变形，最大位移发生在瞳孔位置，有利于缓解前后房压差。如果瞳孔发生后粘连，虹膜中部隆起，在5 μm虹膜-晶状体间隙的前后房压差作用下，虹膜已经有明显的膨隆。数据拟合结果表明当虹膜-晶状体间隙小于3 μm后，能形成显著虹膜膨隆，导致虹膜前表面与角膜内表面接触（房角关闭），从而引起闭角型青光眼。

本研究的定量研究结果有助于从生物力学的角度认识人眼虹膜与房水流动的相互作用力学特性，为闭角型青光眼发病机理及诊断治疗提供指导。已有的研究通常进行定性分析瞳孔阻滞，临床中也做了大量研究，如人工晶状体置换改变虹膜-晶状体间隙，使后房压力得以下降，从而有效缓解高眼压对眼部的损害。本研究通过改变虹膜-晶状体间隙进行定量研究，通过计算数据拟合发现3 μm虹膜-晶状体间隙是后房眼压升高及前房角关闭的指导参数，用于指导临床，适时进行手术干预。

本研究为房水流场压力作用下的虹膜变形分析的流固单向耦合分析，研究重点为虹膜-晶状体间隙对前后房眼压差以及虹膜变形的影响，虹膜结构建模为线弹性体，其生物力学参数选取为目前普遍认可的数值。本研究并未涉及疾病状态下个体化数据研究，今后将在该方面以及虹膜非线性模型领域进一步开展研究。

利益冲突申明本研究无任何利益冲突

作者贡献声明曹月红：课题设计，收集数据，资料分析及解释，撰写论文。蔡建程：参与收集数据，资料分析及解释，论文撰写及修改。陈雁翎：参与收集数据，参与修改论文中关键性结果、结论。Volodymyr Brazhenko：参与研究，论文修改。Ievgen Mochalin：数值计算指导，论文修改