选区激光熔化Voronoi 多孔结构的设计与性能预测

曾寿金，吴启锐，何家辰，韦铁平，叶建华

（1. 福建工程学院机械与汽车工程学院，福建福州350118；2. 苏州大学附属第一医院骨科研究所，江苏苏州215006）

1 引 言

对损伤骨组织进行植入体的置换，一直是医学上常用的方式。临床上常采用力学性能较高的金属植入体进行替换，例如不锈钢、钛和钛合金、钴铬合金等金属植入体［1］，用作人工膝关节、牙种植体、人工骨等［2-3］。但是人工植入体存在着远期无菌松动和再骨折现象，研究人员普遍认为“应力屏蔽”效应［4-5］是其主要原因。“应力屏蔽”效应是指金属人工植入体的弹性模量与人体骨头的弹性模量存在着巨大差异，导致应力无法从人工植入体传递到骨组织上。由于人体骨细胞有着应力响应的生物学特性，人工植入体一端弹性模量较大，会承受较多的应力，骨细胞得不到足够的应力刺激时，骨细胞会发生凋亡，从而对健康骨头产生不良影响［6-8］。

人骨小梁的孔隙率在50%～90%之间，弹性模量为0.5～20 GPa［9］，而实心316L 不锈钢的弹性模量为210 GPa，将实心金属设计成多孔结构能够有效地降低金属材料的弹性模量。因此，华南理工大学杨永强团队［10］研究了正八面体和正六面体单元多孔结构的比表面积、孔隙率、平均孔径对抗压强度和弹性模量的影响。重庆大学柏龙［11］等人基于体心立方（Body-Centered Cubic，BCC）多孔结构设计出一种兼具轻质和高强性能的体心四方（Body-Centered Tetragonal，BCT）多孔结构，发现BCT 多孔结构比BCC 在力学上有着更加明显的优势，为多孔结构在工程领域的应用提供了力学理论依据。Simoneau［12］等人提出了一种用于医学应用的随机开放的多孔结构设计、制造和测试的新方法，测定了刚度和抗剪强度均符合数值预期。Yan［13］等人在研究三周期极小曲面和金刚石单元多孔结构时发现三周期极小曲面多孔结构的孔隙率与小梁骨孔隙度相当，弹性模量在0.12～1.25 GPa 内，且可根据小梁骨模量进行调整，从而减少或避免“应力屏蔽”现象，增加植入物的寿命。

选区激光熔化（Selective Laser Melting，SLM）技术［14-16］是成型金属多孔结构重要的增材制造技术。它通过对切片后的模型数据进行路径扫描，利用激光熔化金属粉末，层层累积，可以成型出具有极其复杂几何特征的零件，可以很好地满足医疗领域个性化植入体的需求［17-19］。

天然骨组织是由外部皮质骨和内部骨小梁组成的，它们并不是密实化组织，而是复杂的无规则孔状结构，这些孔状结构的形态各异、性能不同［20］。如何在植入体设计阶段就能考虑成型后制件的力学性能与生物相容性要求，是利用选区激光熔化技术服务于骨科医疗需求的重要课题。为此，本文通过控制不规则多孔结构的设计参数，研究了一种自下而上的多孔结构参数化设计方法，建立了利用不规则多孔结构的结构设计参数预测弹性模量、抗压强度和孔隙率等性能参数的多元非线性数学模型，为医用植入体的研究提供了设计依据。

2 试验方法及多孔结构设计

2.1 试验材料

选用316L 不锈钢粉末，其粒径分布为10～45 μm，对应的欧洲牌号为1.4404。利用扫描电子显微镜对粉末进行观测，316L 不锈钢粉末有很高的球形，如图1 所示，各元素含量如表1 所示。实验前粉末在80 ℃真空干燥10 h 以上。

表1 316L 不锈钢粉末的化学成分Tab.1 Chemical composition of 316L stainless steel powder（wt.%）

图1 316L 不锈钢粉末形貌Fig. 1 Morphology of 316L stainless steel powder

2.2 试验设备

图2 为SLM 工作原理。试验采用的是德国SLM Solution 公司研发的SLM-125HL 成形设备，其中包括激光系统、扫描振镜系统、冷却系统、密封成形缸、铺粉机构以及控制系统。设备的成形缸尺寸为125 mm×125 mm×125 mm，最大功率为400 W，成形精度可达0.01 mm。激光熔化过程中，采用氮气对材料进行保护。成形工艺参数为：激光功率P=250 W、扫描速度v=800 mm/s、扫描间距h=0.08 mm、铺粉厚度d=0.03 mm，基板预热为100 ℃，扫描策略为单向扫描。

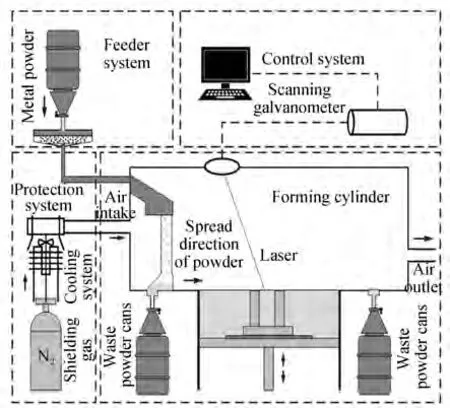
图2 选区激光熔化原理Fig.2 Principle of selective laser melting

2.3 不规则多孔结构设计

图3 概率球模型Fig.3 Probability ball model

Voronoi 是几何计算中一种常见的方法。它基于在空间或平面上随机生成的种子点［21］，通过特定的算法将种子相互连接，形成类似于细胞的多边形，从而实现空间或平面的分割。对于不规则性的定义目前尚未统一，本文从种子在Voronoi 空间区域的分布出发，探讨了孔隙结构的不规则性。规则概率球的球面中心与不规则点的关系如图3（a）所示，其中R为概率球的半径，在概率球内部及其表面会按照函数关系（表2）随机生成不规则点。Ki为相邻概率球之间的距离（即单元距离），Li是概率球心与随机点之间的距离（图3（b））。I被定义为不规则度，则有：

其中N为种子点数。本研究的不规则多孔结构的空间点数均为7×7×7，共计343。

本文利用参数化建模软件Grasshopper 对不规则多孔结构进行设计。其过程为：（1）生成规则点阵，如图4（a）所示；（2）通过调整概率球的直径来改变种子的不规则度，概率球直径越大，随机点运动的范围越广，种子的分散程度就越高，如图4（b）和4（c）所示；（3）通过Voronoi 几何算法生成完全互联的不规则多孔结构骨架，如图4（d）和4（e）所示，并对骨架进行包边，得到的模型如图4（f）所示。

表2 概率球随机函数Tab.2 Probability sphere random functions

图4 不规则多孔结构设计过程Fig.4 Design process of irregular porous structure

2.4 力学性能测试

SLM 制备样件完成后如图5（a）所示，样品被线切割、清洗、和干燥。利用扫描电子显微镜观察显微结构，如图5（b）～5（c）所示，多孔结构表面会有少量未熔化的粉末和挂渣，这是SLM技术成形造成的，样件表面没有裂纹、缺损，成型效果较好。采用中国长春机械院研发的SDS100型电液伺服疲劳试验机测得多孔结构的弹性模量和抗压强度，压缩试验满足ISO-13314∶2011标准，压缩速度为1 mm/min。平台应力（σpl）被确定为20%～40%压缩应变的算数平均值，可表示为抗压强度。弹性模量被称为多孔金属材料的表观弹性模量，由20%～70% 平台应力（σpl）之间连接直线的斜率确定，如图6 所示。

图5 SLM 制备的316L 不规则多孔结构样件及其SEM 图像Fig.5 As-built 316L irregular porous structure by SLM and its SEM images

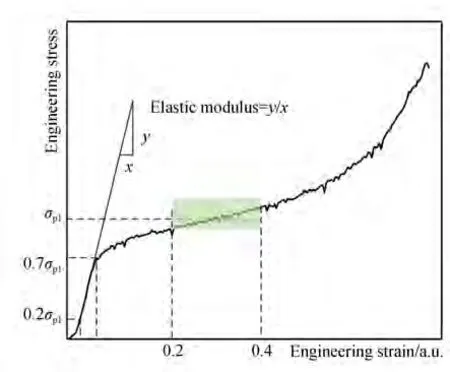
图6 多孔结构的应力-应变曲线Fig.6 Stress-strain curve to determine characteristic values from compression testing of porous structure

2.5 响应面试验

响应面法（Response Surface Method，RSM）是一种试验综合设计的优化方法，最早于1951 年由数学家George E.P.Box 和K.B.Wilson 提出。响应面法通过较少的试验次数，建立了输入变量与输出变量之间的函数关系，通过分析多元回归方程寻求最优结果。RSM 包括中心复合表面设计、中心复合有界设计、中心复合序贯设计以及BOX-Behnken 设 计（BOX-Behnken Design，BBD）。

图7 三因素BBD 试验中试验点分布示意图Fig.7 Distribution diagram of test points in three-factor BBD experimental

BBD 是由2n个设计与不完全区域组合设计组合而成，相同水平时会比中心复合设计拥有更少的试验次数，其设计不包含立方体的顶点，即各变量的极值点，三因素试验中各点分布如图7所示。BBD 是球形设计，具有可旋转或近似可旋转性，没有序贯性，所有因素不会被同时安排为高水平的试验组合，此设计比较适用于对安全要求较高或有特别需求的试验。

本文选择了RSM 的BBD，试验参数如表3所示，因素分别为孔棱直径（D）、不规则度（I）和单元距离（K）。表中，“-1”代表低水平，“0”代表中心点，“+1”代表高水平。

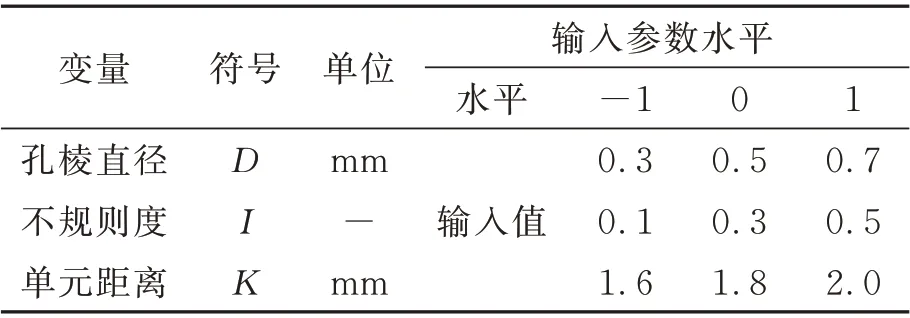
表3 结构参数的水平编码及真实值Tab.3 Horizontal encoding and true values of structural parameters

3 实验结果及数据处理

3.1 实验结果

SLM 成功制备样件后，测得相关参数如表4所示。其中，E表示弹性模量，σ表示为抗压强度，Φ表示为孔隙率。

3.2 实验数据处理

3.2.1 数据归一化处理

对弹性模量、抗压强度和孔隙率3 个响应值进行归一化处理，能够避免因单位的不同对结果的影响。在多孔结构制备实验的过程中，弹性模量具有望小的特性，而抗压强度和孔隙率具有望大的特性。抗压强度和孔隙率的归一化计算公式为：

弹性模量的归一化计算公式为：

式中：n为响应面的目标数；i为实验组数；xi(n)为参考序列(n)为比较序列。

表4 BBD 试验结果Tab.4 BBD experimental results

3.2.2 灰色关联系数计算

对于参考序列和比较序列之间的灰色关联系数（Grey Relation Coefficient，GRC）计算为：

式中：Δ(n)被成为偏差数列，表示参考数列与比较数列的差值，即Δ(n)=|xi(n)-(n)|；Δmin和Δmax分别表示偏差数列的最小值和最大值；ξ为分别系数，通常取值为0.5。

3.2.3 主成分分析及响应值权重

在进行多目标分析的过程中，确定各响应值的权重是需要实验数据进行降维处理。主成分分析法能够从实验数据中得到各因子对响应值的影响程度，是一种十分有效的数据降维处理，从而确定响应值的目标权重。

（1）构造响应值样本矩阵：

式中：t为响应值目标数，t=3；m为实验组数，m=17。

（2）计算相关关系系数矩阵Rjk，Rjk=[rjk]，

式中：rjk为关系系数矩阵中的各元素；Cov[xi(j)，xi(k)]为xi(j)和xi(k)的协方差；σ[xi(j)]和σ[xi(k)]分别是xi(j)和xi(k)的标准差。

（3）特征值求解得到：

式中：E为单位矩阵；λk为关系系数矩阵Rjk的特征值，特征值根据大小排列，即λ1＞λ2＞…λk＞0，k=1，2，…，n。

（4）计算主成分贡献率ak：

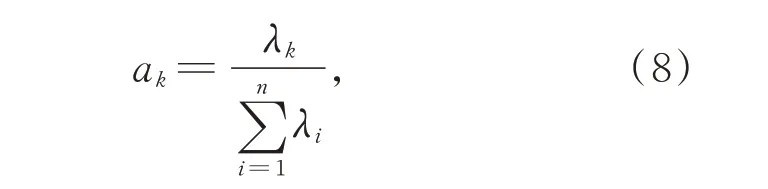
式中ak为各响应值的权重。对各响应进行主成分分析，结果如表5 所示。

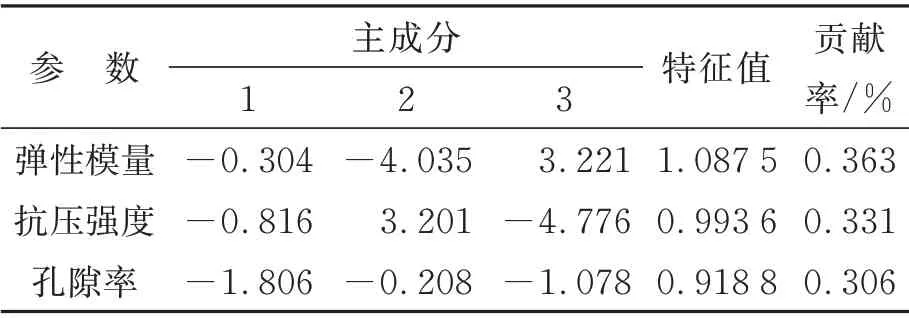
表5 主成分分析结果Tab.5 Results of principal component analysis

3.2.4 灰色关联度计算

表6 BBD 实验数据处理结果Tab.6 Result of BBD experimental data processing

3.3 灰色关联度预测模型

本文采用多元回归分析函数（公式（9））建立和分析输入参数和输出结果的模型：

其中：y为响应值，β0为截距因子，βj，βij，βjj分别是线性项、相互作用项和二次项的系数，xi，xj表示处理参数，k为因子个数，ε为残差。通过响应面设计，建立一个基于试验结果的不规则多孔结构参数与GRG 之间的统计预测模型。利用Design-Expert（V8.0.6.1）软件得到GRG 的预测模型：

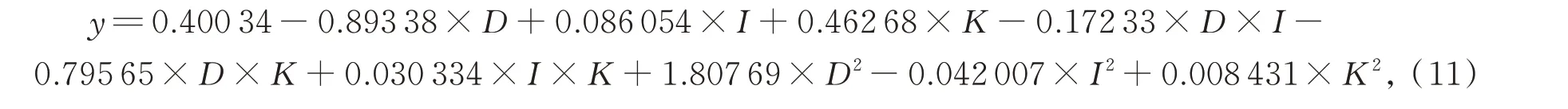
其中：线性效应项D为孔棱直径，I为不规则度，K为单元距离，D×I，D×K，I×K是相互作用项，D2，I2，K2是二次项。在进行有效性筛选时，P＞F值小于0.05 被评价为显著项。GRG 模型中各项的F值和P＞F值如表7 所示。计算得到R2为0.975 9，PredR2为0.934 6，信噪比为17.488，AdjR2为0.944 9。

表7 各项式估计值与P＞F 值表Tab.7 Estimates of each formula and P＞F values

表中，模型决定系数R2，PredR2，AdjR2均大于0.9，表明模型有较高的拟合度，P＞F值均小于0.000 1，说明该数学模型拟合方程的预测精度较高，可以准确地找到输入与输出之间的关系。图8 为模型预测值与实际值的对比，可以看出，数据点分布在参考线附近，说明预测值与试验值的差距较小，该模型的精度较高。

图8 模型的预测值与实际值Fig.8 Predicted and actual values of proposed model

4 结果讨论与分析

4.1 结构参数对弹性模量与孔隙率的影响

图9 展示了结构参数对弹性模量与孔隙率的影响。多孔结构主要由气相和固相两部分构成，分别对应于孔隙率和孔棱直径。对于多孔结构的弹性模量和孔隙率，Gibson 和Ashby 两位学者研究做了大量研究，并发现弹性模量和孔隙率之间存在幂函数关系。Gibson-Ashby力学模型［10］如下：

孔棱直径对弹性模量和孔隙率的影响十分显著，随着孔棱直径的增大，多孔结构的孔隙率越来减小。这是因为孔棱直径的增加，多孔内部的固相增加，在多孔结构外轮廓不变的情况下，气相必然会减小，如图10 所示，在孔棱直径不断增大的过程中，多孔结构内部孔洞逐渐减小，并趋于密实化。随着孔隙率的减小，弹性模量会增大。不规则度和单元距离对弹性模量和孔隙率的影响较小，不规则度和单元距离与弹性模量呈负相关性，与孔隙率呈正相关性。

图9 结构参数对弹性模量和孔隙率的影响Fig.9 Influence of structural parameters on elastic modulus and porosity

图10 不同孔棱直径对孔隙率的影响Fig.10 Influence of different strut diameters on porosity

4.2 结构参数对抗压强度的影响

图11 展示了结构参数对抗压强度的影响。结果显示，孔棱直径对多孔结构的抗压强度的影响十分显著，抗压强度随孔棱直径的增大而增强。不规则度和单元距离的增大会影响多孔结构的稳定性，导致抗压强度变弱。如图12 所示，在不规则度由小增大的过程中，多孔结构单元由均匀、规则的立方体逐渐变为不规则的多面体，部分元胞会发生畸变，导致局部元胞的尺寸变化程度加剧，元胞畸变较大的部位的应力集中现象较为突出，最终导致多孔结构抵抗外界载荷的能力变弱。

图11 结构参数对抗压强度的影响Fig.11 Influence of structural parameters on compressive strength

图12 不规则度对抗压强度的影响Fig.12 Influence of irregularity on compressive strength

优化因子及预测响应如表9 所示。试验时，选用最大期望的结构参数，孔棱直径0.3 mm，不规则度为0.5，单元距离为2 mm，验证组应力-应变曲线如图13 所示。在疲劳试验机对多孔结构施加载荷的过程中，初期阶段以多孔内部弹性变形为主要形式，此阶段应力-应变曲线呈现出线性增长。继续增加载荷，316L 多孔样件进入局部变形阶段，多孔结构被逐渐压缩成密实状态，此时应力的增长趋于平缓，直至多孔结构被压缩成完全密实化的样件。通过对模型预测值和试验值的对比，验证GRG 预测模型。误差为预测值与试验值的绝对差除以预测值计算。验证实验中灰色关联度用第三节所述方法计算为0.789 5，误差为1.2%，其中弹性模量为2.987 GPa，抗压强度为210.048 MPa，孔隙率为89.43%。

表8 优化标准和目标Tab.8 Optimization criteria and targets

表9 预测结果与试验验证Tab.9 Prediction results and experimental verification

图13 验证组的应力-应变曲线Fig.13 Stress-strain curves of test group

5 结 论

本文基于Voronoi-Tessellation 原理设计的不规则多孔结构，利用参数化软件Grasshopper实现了多孔结构设计的个性化和特殊化需求。SLM 制造的不规则多孔结构表现出良好的性能，其弹性模量为3.084～5.386 GPa，抗压强度为218.014～378.595 MPa，孔隙率为50.85%～88.31%。与人骨的弹性模量3.65 GPa、抗压强度119 MPa 相比，不规则多孔结构能够满足骨组织的性能需求。设计了BOX-Behnken 实验，并结合灰色关联分析确定了预测值数学模型，方差分析的决定系数R2，PredR2，AdjR2均大于0.9，预测模型具有较好的拟合性。试验结果表明，孔棱直径是影响多孔结构力学性能和孔隙率的主要因素，弹性模量、抗压强度均随着孔棱直径的增大而增大，孔隙率则随孔棱直径的增大而减小；单元距离和不规则度与弹性模量和抗压强度呈负相关性，与孔隙率呈正相关性，但影响程度较小。通过灰色关联分析优化得到的最优结构参数如下：孔棱直径0.3 mm，不规则度0.5，单元距离2 mm。采用最优结构参数制备不规则多孔结构，其弹性模量为2.987 GPa，抗压强度为210.048 GPa，孔隙率为89.43%，GRG 为0.789 5，优化结果与预测结果的符合程度较高，误差仅为1.2%。