改进乌鸦算法的二维Tsallis熵多阈值图像分割算法
常君杰,李东兴,钟欣,杜文汉,王倩楠
(山东理工大学 机械工程学院,山东 淄博 255049)
图像分割是指把图像分成具有不同特性的各个区域,提取出所需目标的过程[1]。阈值法因简单、高效,在图像分割领域应用广泛[2]。近几年,阈值分割方法大都与熵结合使用,Tsallis熵受非广延统计物理的启发,通过引入参数q来度量系统的不可扩展性[3-4]。Sahoo等[5]提出了基于二维Tsallis熵的图像阈值分割方法,充分利用了图像的灰度分布、空间邻域分布等信息,分割效果好,但存在速度慢、计算时间长的缺点。
为加快阈值选取速度,人们将启发式优化算法与熵结合,用于图像分割,取得了较好的效果[6]。文献[7]将萤火虫算法(firefly algorithm, FA)与二维熵结合对图像进行快速分割,减少了运行时间,但需设置的参数多,适用性不强;文献[8]利用自适应布谷鸟算法和二维最大类间方差法进行阈值分割,进一步缩短运行时间,却易陷入局部最优;文献[9]将乌鸦搜索算法用于多阈值图像分割,需设置的参数少,容易实现,可沿较优路径搜索,但传统乌鸦算法位置更新策略为个体随机搜索,存在盲目性,导致乌鸦算法收敛速度慢和易陷入局部最优[10]。
针对乌鸦算法存在的问题,本文提出改进乌鸦算法优化二维Tsallis熵多阈值图像分割法,利用Levy飞行策略优化乌鸦搜索算法,将改进乌鸦搜索算法与二维Tsallis熵结合用于图像分割,以提高二维Tsallis熵多阈值图像分割效率和精度。
1 乌鸦搜索算法及其改进
1.1 乌鸦搜索算法
乌鸦搜索算法(crow search algorithm, CSA)由Askarzadeh[11]提出,是一种基于乌鸦觅食过程的智能算法。乌鸦i为了获取更多食物,会跟踪其他乌鸦j并偷取食物,若乌鸦j发现被跟踪,则会随机飞行迷惑跟踪者i,保护食物不被发现。乌鸦i的位置可表示为
xi,iter+1=

(1)
式中:ri、rj是0和1之间的随机数;iter表示当前迭代次数;mi,iter表示乌鸦i记忆中最优的位置;xi,iter表示乌鸦i当前位置;fli,iter表示飞行长度;APj,iter是迭代时j的感知概率。
更新mi,iter的公式为
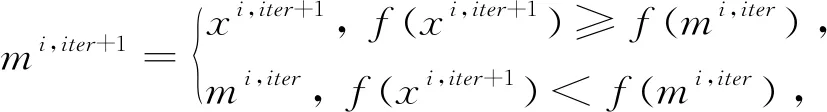
(2)
式中f(·)表示适应度函数。
1.2 改进的乌鸦搜索算法
CSA具有结构简单、易于实现的优点,已成功应用于配电网导体选择[12]、极限学习机参数优化[13]等多个领域。但传统乌鸦算法位置更新策略存在个体随机搜索、具有一定盲目性的问题,导致乌鸦算法收敛速度慢和易陷入局部最优。
1.2.1 Levy飞行机制
Levy飞行是一种随机步长服从Levy分布的方法,具有随机游走、随机发现的特性[14]。利用Levy飞行优化CSA,可以在扩大算法的搜索范围、保持局部搜索能力的同时,有效避免算法陷入局部最优。其幂次形式为
levy(λ)~|s|-λ,1<λ<3。
(3)
本文采用Mantegna提出的Levy步长公式[15]

(4)
(5)
式中δμ、δν定义为
(6)
其中Γ为标准Gamma函数。
1.2.2 自适应Levy飞行策略优化乌鸦搜索算法
利用自适应Levy飞行策略对乌鸦的位置进行更新,即
xi,iter+1=
(7)
式中:⊕表示点乘积;α(iter)为自适应尺度系数,且
(8)
其中β是限制因子,通常为大于1的数。图1为不同β时α(iter)的变化曲线。图1表明,不同的β值均能使α(iter)满足在前期保持一个相对较大的初值,并随迭代进行逐渐减小的条件,且随β值增大,α(iter)后期衰减速率越快,效果越好;但β值的增大使算法计算量增加,影响算法的实时性。通过大量实验验证可知,β=3时可以使α(iter)有较快衰减速率的同时保证算法的实时性。
由计算所得的轴承静载荷及动载荷,选取轴承型号为22310C/W33,其额定动载荷为175 kN,静载荷为210 kN,满足要求.
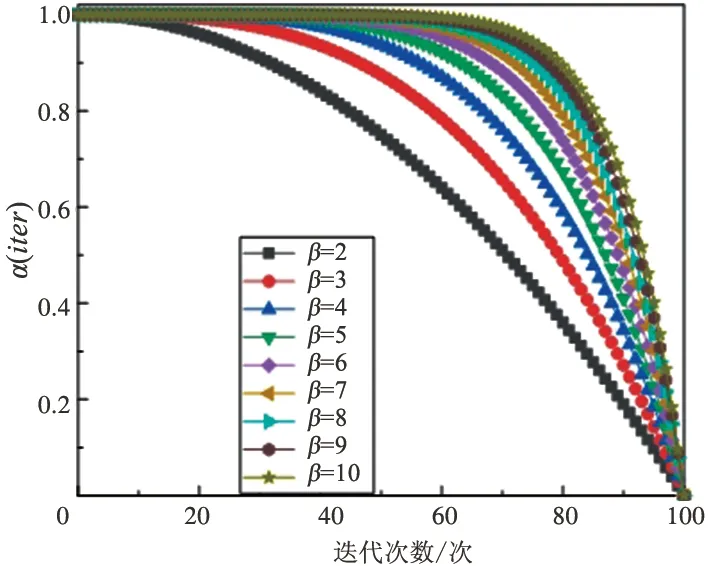
图1 尺度系数变化图
图1显示,α(iter)的变化是非线性的,在算法初期,迭代次数较少,α(iter)在较长的时间内保持较大的值,使得Levy飞行以较大步长进行搜索,全局搜索能力较强,便于找到近似的全局最优解;算法运行后期,解接近最优解时,α(iter)的值急剧减小,自适应缩小搜索步长,利于在最优解附近精细搜索,加速算法收敛。
传统CSA中,当rj 假设I(x,y)为待处理图像,用n个灰度级阈值(s1,t1),…,(sn,tn)将I(x,y)的二维直方图P(i,j)划分为n+1个类{A1,A2,...,An+1},如图2所示。 图2 二维多阈值直方图 目标区Ak中灰度级所对应的概率为 (9) 传统二维Tsallis熵多阈值分割采用穷举的搜索模式,设图像的灰度级数为L,阈值个数为n,则时间复杂度为O(L2n),复杂度随着阈值数的增加呈指数级增长[17]。本文提出改进CSA的二维Tsallis熵多阈值图像分割方法,把分割阈值选择的问题转变为改进CSA对二维Tsallis熵函数Sq((s1,t1),(s2,t2),...,(sn,tn))的寻优问题。设算法的种群规模为N,问题维度为n,迭代次数为itermax,则算法的整体复杂度为O(itermax×N×n),远远小于O(L2n),因此改进算法能在较短时间内给出可行解或者近似最优解。 改进CSA的二维Tsallis熵多阈值图像分割算法流程图如图3所示,具体步骤如下: 图3 多阈值分割流程 步骤1:初始化基本参数,即种群数量N、最优阈值向量的维数n(根据选取的阈值个数确定)、感知概率AP、飞行长度fl及最大迭代次数itermax; 步骤2:随生成N只乌鸦的初始位置,算法初期由于乌鸦都没有“记忆位置”,所以令mi=xi; 步骤3:利用式(7)对乌鸦位置x进行更新,并计算新位置的适应度; 步骤4:根据式(2)更新记忆位置m,若f(xi,iter+1)≥f(mi,iter),则mi,iter=xi,iter+1,否则保持不变; 步骤5:判断是否满足条件,若未满足最大迭代次数,回到步骤3,反之继续进行步骤6; 步骤6:输出最优阈值(s*,t*),并以此分割图像。 为验证改进CSA在图像分割效果和计算时间上的优越性,本文将Lena和Peppers典型图像作为实验对象进行多阈值图像分割。通过大量实验验证,本文选取参数种群规模N=20,最大迭代次数itermax=100,感知概率AP=0.4,飞行步长fl=2。 用改进CSA对Lena图进行二维Tsallis熵的分割,分割结果如图4所示。从图4中可以看出,采用单阈值分割图像时,分割结果粗糙,背景中的细节被忽略,头发细节处分割模糊;采用二阈值分割时,背景中被忽略的细节有所体现,但帽子处的分割效果不理想;采用三阈值分割时,分割效果较好,分割结果清晰,局部细节好。因此,本文算法能有效分割复杂图像,且随阈值的增加,分割效果越好,得到的有用信息越多。 (a) 原图 (b) 单阈值 为进一步验证改进CSA的性能,将改进CSA与文献[7]中的FA和文献[9]中的经典CSA进行二维Tsallis熵分割对比实验,对Peppers图像进行分割,以阈值n=3为例,分割结果如图5所示。 (a) 原图 (b) FA结果 从图5中可以看出,FA分割后青椒上的细节严重丢失,传统CSA分割后局部区域过亮和过暗,分割效果不理想;改进CSA分割后图像局部细节明显好于其他2种算法,展现的信息更为清晰,分割效果更好。 为定量分析3种算法的性能,采用峰值信噪比(peak signal to noise ratio, PSNR[18])与结构相似性 (structural similarity index, SSIM[19])对分割后图像的性能进行比较。灰度图像x(i,j)及阈值分割后图像y(i,j)的PSNR定义为 (10) 式中: (11) 通常分割效果越好,PSNR值越大。 SSIM用来衡量两幅图像的相似度。原始图像x与分割后的图像y的结构相似性可按照下式求出: (12) 表1中数据显示,当阈值个数为1时,各算法均顺利找到了最佳阈值,分割效果相近。但当阈值个数为2、3时,本文算法的优势体现出来,分割结果更加准确。以3阈值为例,本文算法分割Peppers图像后的PSNR较FA与传统CSA分别提高了12.68%、4.41%;SSIM分别提高了15.58%、12.73%。因此,相较对比算法,改进后CSA在分割精度上具有明显优势。 表1 阈值、PSNR及SSIM的对比 为了直观反映3种算法的收敛过程,在itermax=100,n=3的情况下,绘制出Peppers图的收敛曲线,如图6所示。表2为不同算法在不同阈值条件下的分割结果。 图6 Peppers收敛过程图 从图6中可以看出,FA和传统CSA分别在第18次、第22次进行局部精细求解,陷入局部最优,虽最终均跳出了局部最优,但迭代次数增加,收敛速度较慢。表2中数据显示,对Peppers图像进行3阈值分割时,改进算法在第35次迭代时已经收敛到最优值,明显早于其他算法,且算法运行时间最短,FA与传统CSA所用时间分别是改进算法的2.76倍、1.14倍。 表2 适应度值、运性时间以及迭代次数的对比 综合图6与表2中的数据可知:改进后的CSA在运行过程中未陷入局部最优,迭代次数少、收敛速度快,且收敛后的目标函数值远高于其他2种算法;改进后的CSA能较好地引导个体趋于全局最优解,相较其他2种算法在收敛速度以及分割精度上都有明显改善。 1)建立了一种自适应Levy飞行搜索策略。利用Levy飞行随机游走的特性帮助CSA跳出局部最优,设置尺度系数自适应地限制Levy飞行搜索步长,平衡算法的全局寻优能力和局部精细求解能力,加速算法收敛。 2)利用改进乌鸦搜索算法优化二维Tsallis熵多阈值图像分割,能减少计算量,提高运算效率,大大缩短分割时间。 3)将FA、传统CSA与本文算法进行对比实验。实验结果显示,改进CSA较其他算法分割清晰,细节特征保留完好,收敛速度快,计算时间短,不易陷入局部最优,PSNR与SSIM值均高于其他2种算法,验证了改进CSA算法的有效性。2 改进CSA优化Tsallis熵分割算法
2.1 二维多阈值Tsallis熵分割算法



2.2 改进CSA优化Tsallis熵分割算法
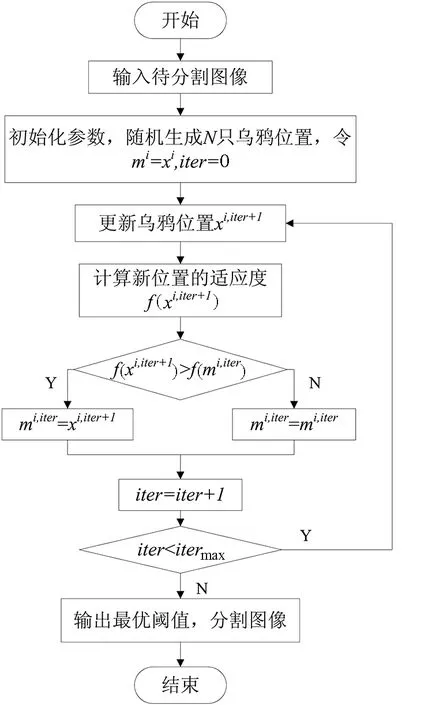
3 实验结果与分析
3.1 多阈值图像分割实验


3.2 分割性能对比





4 结论

