基于参考模型的主动悬架反演控制设计

李连正，秦志昌，郭宗和，李瑞先，荆栋

(山东理工大学 交通与车辆工程学院, 山东 淄博 255049)

随着汽车工业的飞速发展，汽车的安全性能得到了极大的提高，越来越多的汽车生产厂家开始关注噪音以及振动等关于汽车舒适性的性能指标[1]。悬架作为汽车中必不可少的部件之一，在提高乘坐舒适性以及行驶稳定性方面起着不言而喻的重要作用[2-4]。主动悬架相较于传统广泛使用的被动悬架，在外部能量输入的作用下能够让悬架系统在不同路面激励的情况下始终保持良好的减振效果，同时能兼顾汽车的行驶稳定性。

主动悬架性能的好坏与其控制策略的优劣有着直接的联系，因此设计和选择与主动悬架相匹配的控制策略显得尤为重要[5]。运用于主动悬架系统的控制方法主要有滑模变结构控制[6-8]、最优控制[9]、模糊控制[10]、反演控制[11-12]、PID、LQR[13-14]控制等。其中，传统的PID、LQR控制器设计因结构简单而得到广泛应用，然而其控制性能较为有限。

在诸多控制方法中，反演控制是一种比较成熟的控制器设计方法。其基本设计思想是将复杂系统分解成不超过系统阶数的子系统，然后基于李雅普诺夫稳定性理论，在保证每个子系统具有一定收敛性的基础上获得子系统的虚拟控制率，在下一个子系统的设计中将上一个子系统的虚拟控制率作为这个子系统的跟踪目标，以递推的方式获得最终控制率。控制器设计过程中所采用的虚拟控制率无需通过硬件实现，可直接由计算得到。因设计过程具有系统化、结构化的特点，所以基于反演控制方法所设计的控制器往往结构比较简单且易于实现。

由Krstic等[15]的著名论文为起点，反演法目前已经成为解决线性及非线性系统控制问题的一种非常有效的方法。文献[16]基于反演控制理论设计了电流反演控制器和速度反演控制器，用于永磁同步电机调速系统。文献[17]利用反演控制方法结合反馈线性化设计了一种飞行器自适应飞行控制系统。文献[18]基于自适应积分反演控制方法研究在未知海流作用下水下航行器的运动跟踪控制问题。这些研究表明，反演控制在解决这类复杂跟踪控制时具有良好效果。在悬架系统研究中，文献[19]在忽略轮胎阻尼特性的前提下着重考虑了悬架系统中的不确定性因素，以悬架动行程为零作为设计目标进行了控制器设计，最终实现了减小车身振动的目的。

对基于参考模型的反演控制方法的研究，国内外学者们也已经取得了许多成果。文献[20]基于模型参考反演控制设计了一种自适应控制器，并应用于一种变压器绕组系统。文献[21]以天棚阻尼系统作为参考模型，以参考模型的输出为期望值进行控制设计，减小了车身垂直加速度。文献[22]通过引入高低通滤波器设计了一种理想的参考模型系统，结合反演控制设计了误差跟踪反演控制器，提高了悬架系统的性能。众多研究结果表明，基于反演法以及基于参考模型的反演法的控制器设计在解决汽车悬架振动控制问题上具有良好效果。

本文利用反演控制具有良好目标跟踪效果的特性，设计一个混合阻尼(天棚-地棚阻尼)悬架系统(该悬架系统现实中难以实现，但有良好的减振控制效果[23-24])作为参考模型，通过反演控制方法对参考模型系统的输出信号进行追踪[25]，设计一种基于参考模型的反演控制器并进行仿真验证。

1 1/4车辆主动悬架系统模型

根据Quanser实验台架，建立1/4汽车主动悬架模型，如图1所示。

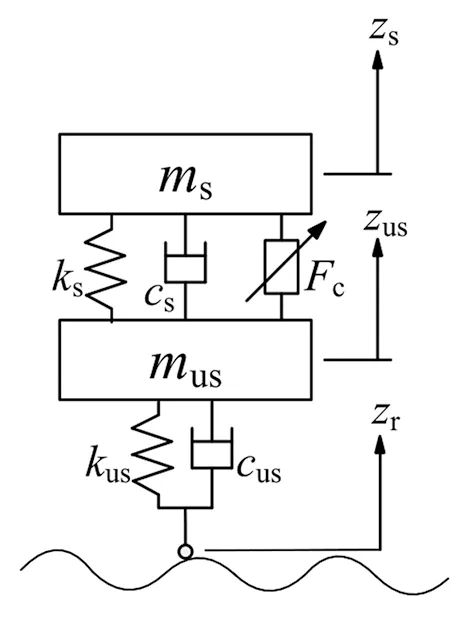
图1 二自由度1/4汽车主动悬架模型

该系统由两个质量组成，每个质量由一个弹簧和一个阻尼器支撑。簧载质量ms表示车身质量，非簧载质量mus表示四分之一车的轮胎悬架系统由弹簧、阻尼器、控制器组成，ks、cs、Fc分别表示悬架弹簧刚度、悬架阻尼器阻尼、控制器输出主动力，kus、cus分别表示轮胎的等效刚度及阻尼。主动力Fc以及路面激励zr为系统的两个输入。因重力只影响系统的静平衡点位置，所以取广义坐标，zs和zus分别表示车身和轮胎相对于其处于静平衡位置的位移，取向上为正方向。根据牛顿第二定律，得到系统的动力学方程为

为了方便控制器设计，将悬架系统通过状态空间表示，写成如下形式：

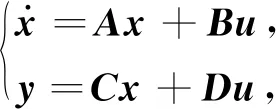
(2)

式中，状态变量、系统的输入和输出变量定义为

(3)

状态变量x中的4个分量分别表示悬架动行程、车身垂直速度、轮胎变形量、车轮垂直速度，根据方程(1)可以计算出A，B，C，D4个矩阵，即

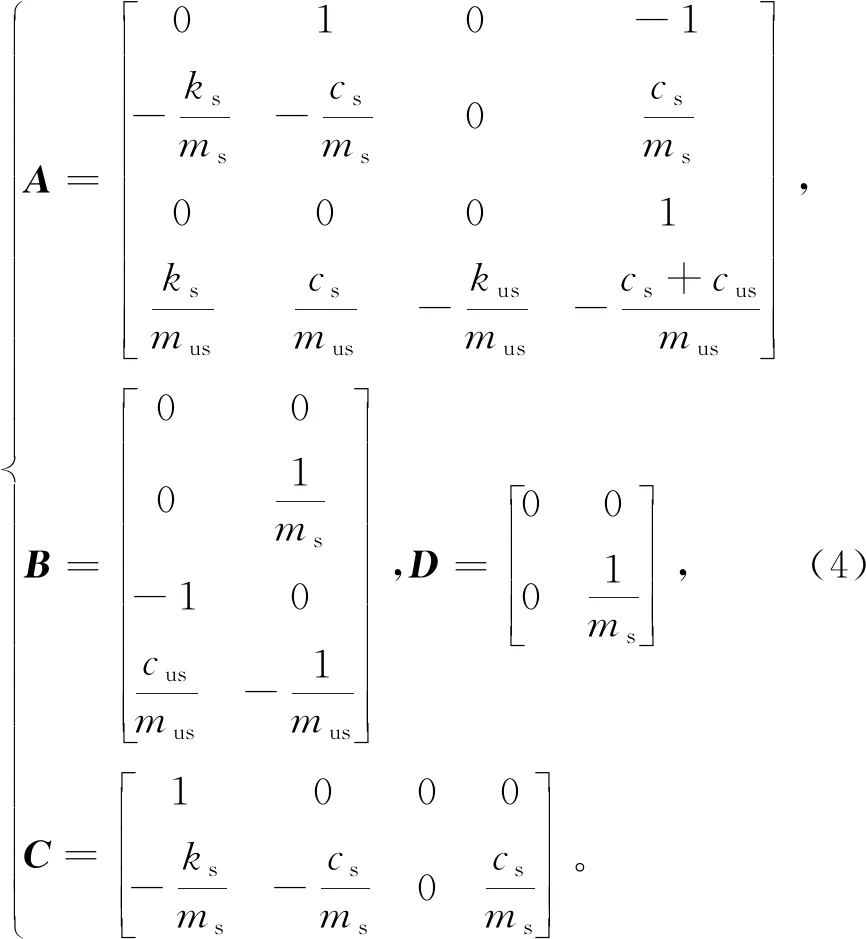
2 控制器设计

为了提高悬架性能，我们对主动悬架控制器进行设计，即对控制器输出主动力Fc进行设计。

2.1 LQR控制器设计

为了同本文所设计的一种基于参考模型的反演控制器进行比较，设计了一个相对简单的LQR控制器。

(5)

定义二次型目标函数

(6)

由最优控制理论可知，反馈控制输入为

Fc=-Kx。

(7)

选取

利用MATLAB控制工具箱，可以计算得到最优控制增益矩阵为

(8)

2.2 反演控制器设计

(9)

对V1求导得

(10)

取误差e2=x2d-x2，其中x2d为x2的期望值，取

(11)

式中k1以及下文中的k2均为正数，将e2代入式(10)得

(12)

选取第二个李雅普诺夫函数

(13)

对V2求导得

(14)

(15)

(16)

取控制输入Fc为

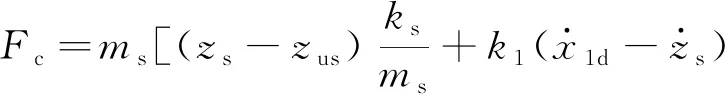
(17)

将方程(17)代入方程(16)得

(18)

因此，受控系统是渐进稳定的，并且随时间趋于无穷大，e1和e2将趋于零。

理想情况下，即当悬架动行程为无限大，或者在不考虑悬架动行程约束的情况时，可以选取zsd=0(车身无垂向运动)，此时车身垂直加速度为0，但理想情况需要控制器能提供非常大的主动力，在现实中难以实现。为了找到一个合适的zsd，考虑选取一个理想的参考模型系统，选取参考模型的输出作为我们的期望值。

2.3 参考模型设计

为了达到减小车身垂直加速度且减小轮胎变形量的目的，考虑一个混合阻尼悬架系统，即在车身与虚拟的惯性空间之间有一个阻尼cy来抑制簧上质量的振动，同时假设在车轮和地面之间有一个阻尼cd来抑制簧下质量的振动，同时保证汽车的平顺性和操纵稳定性，克服单纯的天棚阻尼系统的不足。该参考模型如图2所示。

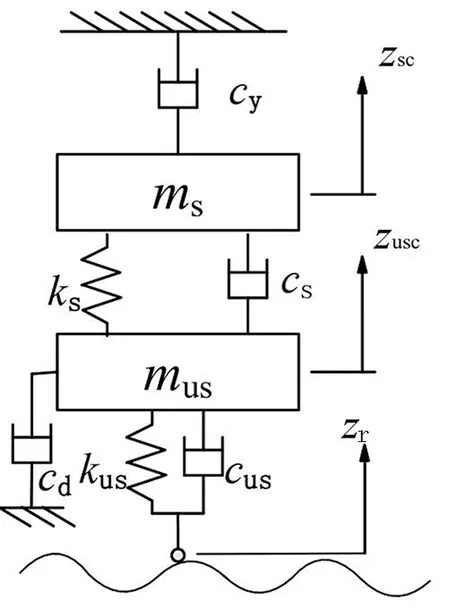
图2 含天、地棚阻尼的1/4汽车悬架参考模型

该系统在图1所示的主动悬架系统的基础上设置控制器主动力为0，同时在车身与虚拟天棚之间设置一个虚拟天棚阻尼 (cy)，轮胎与地面之间设置一个虚拟地棚阻尼 (cd)。zsc、zusc分别表示车身和车轮相对于静平衡位置的垂直位移，取向上为正方向。根据牛顿第二定律得到参考模型系统的动力学方程为

(19)

将悬架系统通过状态空间表示，写成如下形式：

(20)

状态变量、系统的输入和输出变量定义为

(21)

根据方程(1)可以计算出如下矩阵：

根据主动悬架系统模型的阻尼参数，以cs的整数倍分别选取两组虚拟阻尼参数进行对比研究。cy、cd的选值见表1。

表1 参考模型混合阻尼参数

图3和图4分别展示了表1中两组虚拟阻尼作用下参考模型系统的输出，即车身位移曲线和车身垂直加速度曲线。

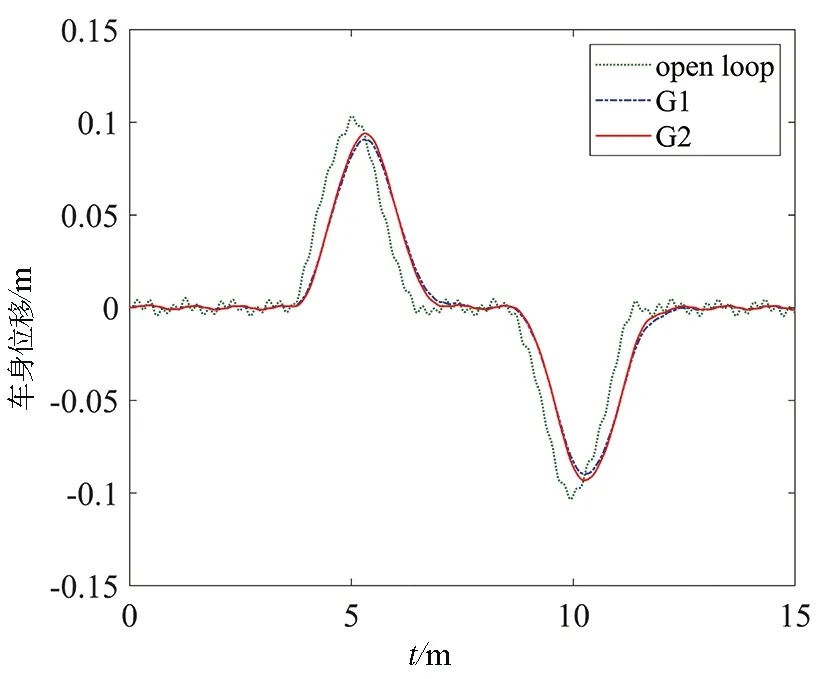
图3 参考模型车身垂直位移

图4 参考模型车身垂直加速度

从图3和图4中可以看出，相对于普通的被动悬架系统，在增加虚拟天棚-地棚阻尼后，车身位移曲线相对光滑，车身垂直加速度明显减小，说明该虚拟阻尼可以有效减小车身垂直振动。

该基于天棚-地棚阻尼的混合阻尼悬架系统只是一种理想的概念模型，在实际环境中并无法直接应用。然而，因其完美的减振性能，国内外诸多研究学者都对其进行了深入研究并通过诸多主动控制方法间接实现了其控制性能。在本文中，我们选择该理想天棚-地棚阻尼控制系统模型作为一种参考模型，将该系统的输出信号作为2.2节所设计的反演控制器的期望值，即

(23)

因此，本文所研究的基于参考模型的反演控制器融合了理想的天棚-地棚阻尼控制器的优良控制性能和反演控制器的稳定性，为主动悬架控制提供了一种新的研究思路。

3 仿真分析

根据已经建立的模型和算法进行仿真模拟。选取车辆1/4试验台架模型参数，对图2主动悬架系统在MATLAB/Simulink中进行仿真，同时与LQR控制下主动悬架控制效果进行对比。主动悬架试验台架参数见表2。

表2 实验台架模型参数

在仿真过程中，根据文献[10]选取一种由路面函数d(t)模拟的正弦扰动叠加在凸起和凹陷的路面函数上作为路面激励，道路的轮廓是时间t的函数，即

3.1 反演控制追踪效果

设定方程(13)中反演控制器的两个参数分别为k1=20和k2=20，然后对图1所示的主动悬架系统进行反演控制，并将其与天棚-地棚阻尼控制结果进行对比。图5和图6分别展示了两种控制策略下1/4悬架的车身位移、车身垂直加速度曲线。

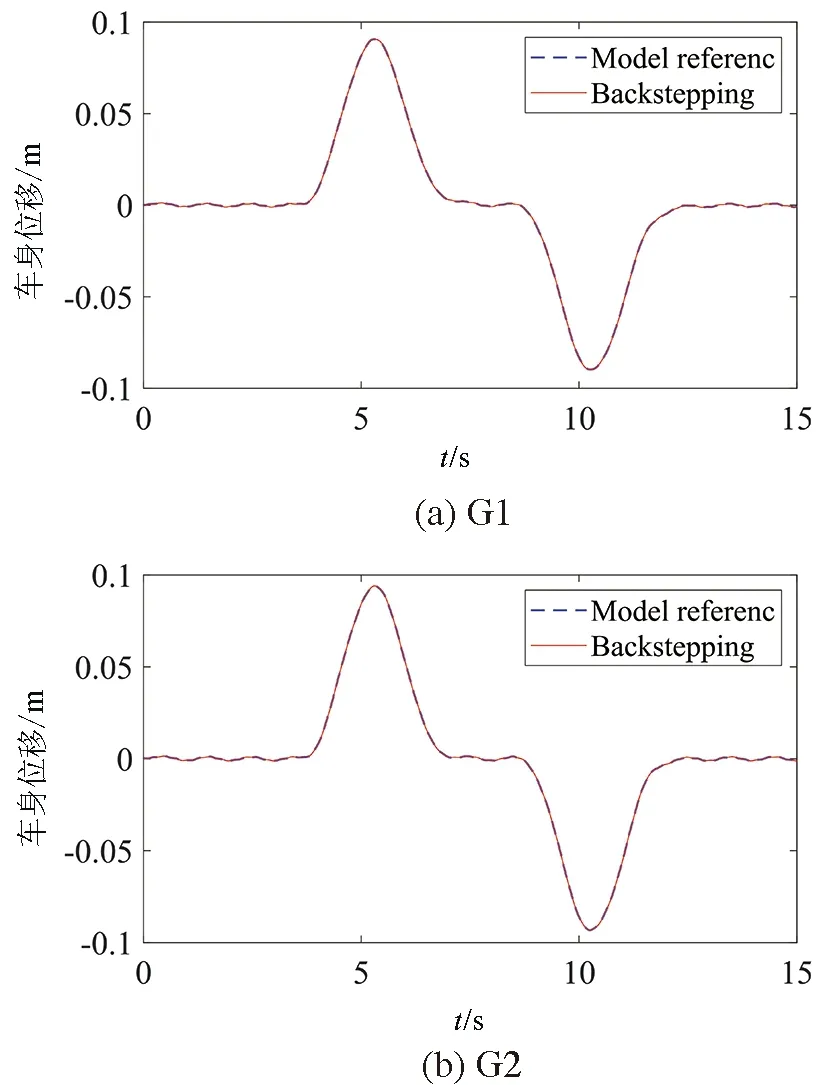
图5 两种控制策略下的车身位移

图5和图6中蓝色线条展示了表1中G1和G2两种情景下悬架系统的理想控制效果，红色线条代表以此理想输出作为参考信号(即以天棚-地棚阻尼控制的被动悬架系统为参考模型)的反演控制下主动悬架系统输出。可以看出，基于反演控制的系统输出与基于天棚-地棚阻尼控制的理想输出之间有较小的误差，两条曲线基本重合，表明所设计的反演控制器可以很好地实现天棚-地棚阻尼控制的效果。

图6 两种控制策略下的车身垂直加速度

仿真结果说明，基于反演控制的主动控制算法可以实现一类无法直接用于实际悬架系统的天棚-地棚阻尼减振控制。

3.2 主动悬架性能分析

图7—图10展示了悬架系统在开环状态、LQR控制和模型参考反演控制下的车身垂直加速度、轮胎变形量、 悬架动行程以及控制器主动力。BG1和BG2分别表示按G1和G2两种情景所设定的被动悬架系统作为参考模型的反演控制。

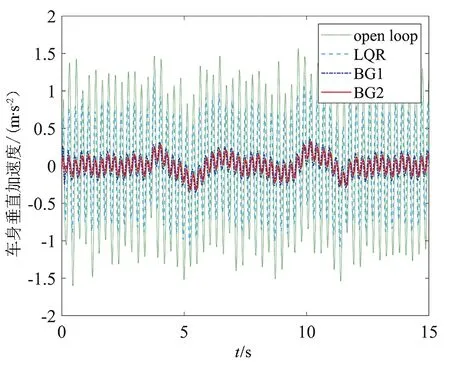
图7 车身垂直加速度

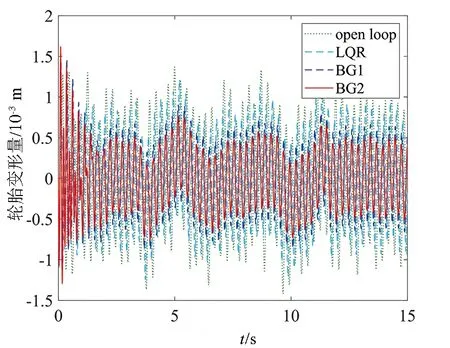
图8 轮胎变形量

图9悬架动行程

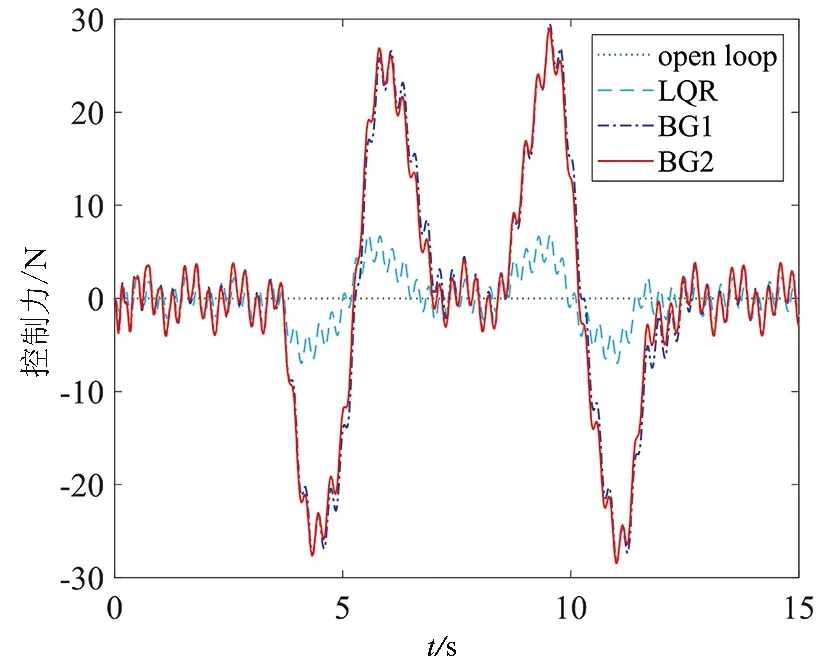
图10 控制器主动力

由图7和图8可以看出，相较于被动悬架系统(即开环系统)，LQR控制方法在减小车身垂直加速度和轮胎变形量方面具有一定的效果。进一步对比可以看出，两组基于参考模型的反演控制器的控制效果要优于LQR控制器。其中，以G2作为参考模型的反演控制在一定程度上要优于以G1作为参考模型的反演控制。

图9和图10分别展示了悬架系统在几种控制策略下的动行程和控制力大小。可以看出，在两组基于参考模型的反演控制器作用下的主动悬架系统的悬架动行程和控制力均大于LQR，而两组反演控制的悬架动行程和控制力相差不大。结果表明，以方程(19)作为路面激励时，1/4车辆主动悬架系统在本文所提出的基于参考模型的反演控制策略的作用下能够实现更好的减振效果。此外，以天棚-地棚阻尼被动悬架系统作为参考模型的反演控制要优于仅以天棚阻尼被动悬架作为参考模型的反演控制。

3.3 控制器参数k1和k2的影响

通过仿真验证了本文提出的基于参考模型的反演控制器的有效性后，我们又对如何选择更优的控制器参数k1和k2进行了简单研究。

为了选择更优的控制器参数，定义一个用于评价反演控制器性能的指标，即

为研究k1和k2在不同取值情况下对系统控制性能的影响，本文将两个参数分别在(0，100)区间均匀离散为40份，将其两两组合为1 600组参数并分别进行试验。基于方程(20)分别计算各组参数下的性能指标值，得到图11。

图11 基于参考模型的反演控制策略的性能指标

从图11中可以看出，选取不同的k1、k2会对控制器的误差追踪效果有一定影响。随着k1、k2的增大，控制器追踪精度在一定程度上有所提高，但在到达一定数值后，k1、k2进一步增大，控制器追踪精度反而会降低。图11中局部放大部分表现了随着k1、k2的变化，在接近完全追踪时，控制器会出现类似超调的现象。

该模型参考反演控制器作用下的主动悬架系统，能实现对参考模型系统的误差跟踪，选取合适的k1、k2可使反演控制器对参考模型的追踪精度达到95%以上。在参数k1=20和k2=20时，恰好处于图11中追踪精度较高的位置，其追踪精度接近98%。从图4和图5中也可以看出，主动悬架系统与理想参考模型系统的响应曲线基本重合，即表明在该参数下的反演控制器具有良好的控制性能。

4 结束语

本文在建立二自由度1/4车主动悬架的基础上，利用李雅普诺夫稳定性理论、采用反演控制的方法，设计了一种基于参考模型的反演控制器，并根据控制模型和仿真算法在MATLAB中建立仿真程序进行控制效果验证。仿真结果表明，利用该方法设计的控制器，在选取合适的控制器参数时，能够有效追踪参考模型信号，使主动悬架减振性能接近理想参考模型悬架系统减振性能。该方法设计的控制器使车身垂直加速度明显减小，提升了汽车的乘坐舒适性，在一定程度上减小了轮胎变形量，从而提高了汽车行驶的稳定性。同时选取更为优秀的参考模型系统可以进一步提高悬架系统的性能。此外，研究表明，k1、k2的取值也对控制效果有着显著影响，后续研究将进一步针对k1、k2以及cy、cd的选取进行多目标优化设计并进行相关实验研究。