不锈钢芯板L 形墙单向压弯力学性能分析

舒兴平 ，李仕杰 ，姚尧 ，伍中君 ，熊志奇

(1.湖南大学 土木工程学院钢结构研究所，湖南 长沙 410082；2.浙江树人大学 城建学院，浙江 杭州 310015；3.中机国际工程设计研究院有限责任公司，湖南 长沙 410007；4.中国联合工程有限公司，浙江 杭州 310052)

0 概 述

近年来，国家大力推广装配式建筑，除了施工方式在创新，用于装配式建筑的材料也在不断创新，不锈钢材料因其造型美观，具有良好的耐蚀性、耐久性，易于维护和全生命周期成本低等特点，被广泛应用于建筑结构中[1]。

不锈钢芯板结构是由远大可建科技有限公司发明的新型装配式建筑结构。不锈钢芯板由不锈钢面板、侧板以及芯管组成，由2 块不锈钢面板夹住阵列排布的芯管采用铜钎焊焊接成一个整体，其结构形式类似于蜂窝夹层板结构，这种结构相对于其他结构形式具有质量轻、稳定性好等优势[2]。不锈钢芯板如图1(a)所示。

从20 世纪90 年代开始，国内外就对双钢板组合柱[3]以及各种类型的组合墙体进行了大量研究[4]。Eom 等[5]研究了矩形和T 形截面双钢板组合剪力墙的滞回性能。马晓伟等[6]对双钢板混凝土组合剪力墙的压弯承载力进行了数值模拟，并提出了简化计算公式。张素梅等[7-8]对一字形短肢多腔钢混凝土组合剪力墙进行了轴压试验研究，并对T 形截面剪力墙的压弯工作机理进行了有限元分析，结果表明试件性能良好。Zhu等[9]对波形钢板剪力墙的轴压性能进行了分析，研究了波形钢板的屈曲模态以及弹性屈曲应力，提出了波形钢板剪力墙轴压计算公式。

本课题组已对不锈钢芯板一字形墙进行了轴压试验研究，并提出相应设计公式[10]，结果表明，一字形墙性能良好，设计公式与试验结果吻合较好。但在实际工程中，构件形式并不局限于一字形，为了满足实际工程需要，L 形和T 形构件均被广泛使用。在工程中，L 形墙往往被布置在结构的四周，构件处于多种荷载共同作用下，有必要对不锈钢芯板L 形墙在多种荷载共同作用下的受力性能进行研究。本文在验证模型正确性的前提下，对不锈钢芯板L 形墙压弯受力性能进行了数值模拟，利用ABAQUS 有限元软件建立了不锈钢芯板L 形墙压弯有限元模型，对其压弯荷载作用下的受力过程与破坏机理进行分析，研究了影响不锈钢芯板L 形墙压弯承载力等性能的关键参数。不锈钢芯板L 形墙是由2 块宽1 m、高3 m 的不锈钢芯板一字形墙焊接而成，如图1(b)所示。

图1 不锈钢芯板及L 形墙

1 有限元模型及验证

1.1 模型建立

采用ABAQUS 有限元软件模拟不锈钢芯板L 形墙在偏心荷载作用下的力学性能。由于不锈钢芯板L 形墙是由2 块不锈钢芯板一字形墙焊接而成，故本文建立有限元模型时是先建立1 块高3 m、宽1 m 的不锈钢芯板一字形墙，再将2 块不锈钢一字形墙组装为不锈钢L 形墙。

不锈钢芯板一字形墙各参数如图2 所示，该示意图中芯管排列方式为正排排列，其中l 为芯板墙高，b 为墙宽，h 为墙厚，tf为面板厚度，tw为芯管壁厚，d 为芯管直径，lny为竖直方向芯管间距，lmz为水平方向芯管间距。

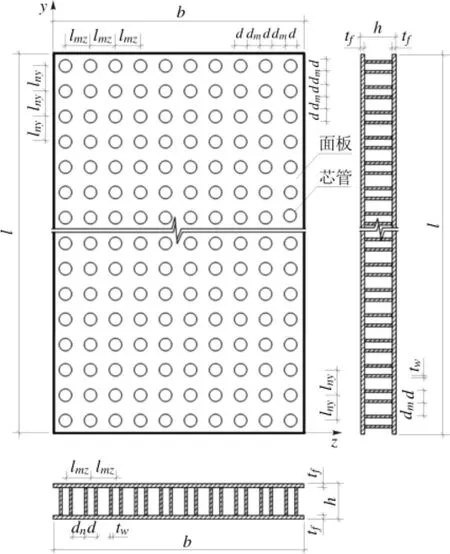
图2 不锈钢芯板一字形墙参数示意

不锈钢芯板L 形墙有限元模型的边界条件如图3 所示，图3(a)中腹板墙肢宽度为b1，翼缘墙肢宽度为b。图3(b)中所示L 形墙的芯管排列方式为错排排列，如无特别说明，本文中一字形墙均为正排排列，L 形墙均为错排排列。

图3 不锈钢芯板L 形墙有限元模型边界条件

为了更好地模拟试验条件，不锈钢芯板L 形墙的上、下表面分别与参考点RP1、RP2 耦合。其中参考点RP2 位于构件底面形心处，且所有自由度均被约束(u=0，ur=0)。参考点RP1 位于构件加载点处，其作用是模拟铰支座，约束RP1x、z方向的自由度以及绕y 轴的转动自由度，并对参考点RP1 施加y 方向的位移进行加载。

本文分析中考虑了几何非线性和材料非线性，由于芯管与面板均属于薄壁构件，可忽略沿其厚度方向即切向的应力，因此有限元模型均采用S4R 四节点壳单元，这种单元会随着壳体厚度的改变，其求解过程会自动满足厚壳理论或薄壳理论。模型的网格均采用四边形网格，其中网格种子密度为20，不锈钢芯板L 形墙有限元模型的网格划分如图4 所示。

图4 不锈钢芯板L 形墙有限元模型网格划分

1.2 材料本构关系

S30403 奥氏体不锈钢是一种超低碳不锈钢，在一般状态下，其耐蚀性与S304 不锈钢相似，但在焊接后其抗晶间腐蚀性能优异，被广泛用于焊接结构。由于不锈钢芯板墙是不锈钢面板与芯管经由铜钎焊焊接而成，使用S30403 不锈钢能使结构具有更好的耐蚀性。

与碳素钢不同，不锈钢材料的应力-应变曲线没有明显的屈服点，在较低荷载下也表现出非线性特征，且呈现出相当大的硬化和较高的延性，是一种典型的非线性材料。不锈钢材料所选用的本构关系模型是修正后的Ramberg-Osgood 模型，该模型由Ramberg 和Osgood 提出，经Hill 进行第一次修正，Mirambel 和 Rasmussen 对其再次修正[11]。

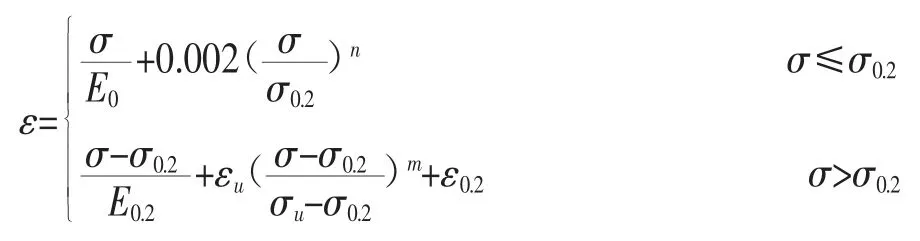
式中：σu——极限应力；

εu——极限应变；

E0——初始弹性模量；

σ0.2——残余应变为0.2%时对应的弹性极限应力值；

CECS 410：2015《不锈钢结构技术规范》中给出的S30403奥氏体不锈钢的力学性能如表1 所示。

表1 奥氏体30403 不锈钢材料的力学性能

1.3 初始缺陷的引入

钢结构构件在实际中会不可避免的出现初始缺陷，如初偏心、初弯曲以及焊接残余应力等。由于初始缺陷的存在，会使构件的真实受力过程与有限元模拟受力过程产生较大的差异。在施加位移荷载之前，先对模型进行屈曲分析，将计算得到的一阶弹性屈曲模态作为初始缺陷引入模型中，最大初始缺陷取墙高的1/1000，即3 mm。

1.4 有限元模型的验证

由于相关试验尚未开展，采用不锈钢芯板一字形墙压弯试验来验证上述有限元模型的合理性。采用上述建模方法对不锈钢芯板一字形墙试件YW6-1、YW6-2，不锈钢芯板L 形墙LW4-1 建立有限元模型并进行分析，试件参数如表2 所示，其中受压侧、受拉侧侧板厚度分别为10.5、2.5 mm。

表2 不锈钢芯板一字形和L 形墙试件尺寸及相关参数

有限元模拟与试验荷载-位移曲线的对比如图5 所示。

由图5 可知，2 个构件的有限元模拟与试验承载力分别相差6.87%、1.76%。但有限元模拟位移比试验位移稍大，可以看出在弹性段模拟与试验斜率保持一致，而在塑性段模拟斜率明显小于于试验斜率，这可能是试验中位移测量有误差。

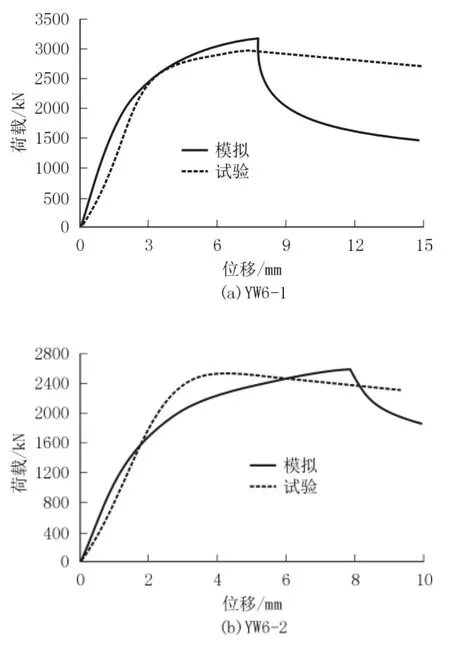
图5 不锈钢芯板一字形墙试验与模拟荷载-位移曲线对比

不锈钢芯板一字形墙试验与有限元模拟破坏形态对比如图6 所示。

图6 不锈钢芯板一字形墙试验与模拟破坏形态对比

从图6 可知，2 个构件的试验破坏形态与有限元模拟破坏形态基本吻合。

2 有限元模型分析

上述分析表明，用此方法建立的有限元模型能较好地模拟不锈钢芯板一字形墙在压弯荷载作用下的受力性能，在此基础上，将此模型用于不锈钢芯板L 形墙压弯性能分析中。采用1.1 节所述建模方法将2 块一字形墙进行组装，建立了不锈钢芯板L 形墙模型(LW4-1)并对其施加偏心荷载，研究其在压弯荷载作用下的受力机理，模型各参数如表2 所示。在进行分析之前先按前述引入初始缺陷，图7 为模型的一阶弹性屈曲模态，下文分析中如无特别说明，不锈钢芯板L 形墙屈曲模态均为图7 所示。图8 给出了LW4-1 的荷载-位移曲线。

图7 不锈钢芯板L 形墙一阶弹性屈曲模态

图8 LW4-1 的荷载-位移曲线

由图8 可知，不锈钢芯板L 形墙压弯受力过程大致可以分为3 个阶段：弹性阶段、弹塑性阶段以及破坏阶段。图8 中点A 对应构件的屈服强度，其荷载为1367.41 kN，位移为2.63 mm。B 点对应试件的极限强度，其荷载为1582.5 kN，位移为4.04 mm。

图9(a)为LW4-1 面板的应力分布，图9(b)为LW4-1 内部芯管的应力分布。图9 中A、B、C 三个状态分别对应图8 中荷载-位移曲线中的 A、B、C 点。

图9 LW4-1 应力分布

由图9 可知，在加载初期，荷载与位移保持线性增长关系，构件处于弹性工作状态，直到加载至屈服点A(N=0.85Nu)。此时面板大部分区域受力较小，只有受压侧上部应力达到130 MPa，而大部分芯管应力处于20 MPa 左右，只有受压侧侧板顶部应力达到182 MPa。

过屈服点后，构件进入弹塑性工作阶段，此时荷载-位移曲线不再呈直线关系，位移增长较快，而荷载增长较慢，其斜率逐渐减小，直至达到极值点B(N=Nu)。此时受压侧面板上部大部分区域达到屈服应力，最大应力为230 MPa；大部分芯管应力较小，只有受压侧上部面板应力大的区域芯管应力大，最大达到197.6 MPa。受压侧侧板顶部发生波浪形鼓曲，如图9(a)中B 所示，最大面外位移为4.89 mm。

过极值点后位移继续增加，荷载却迅速减小，此时构件已经破坏。从图9(a)C(破坏)点的破坏形态可以看出，LW4-1的受压侧面板发生了波浪形鼓曲，而YW6-1、YW6-2 的破坏形态均为受压侧面板发生了直线形鼓曲。这是由于L 形墙与一字形墙的芯管排列方式不同造成的，在没有芯管的位置，面板更容易发生屈曲，面板发生屈曲后沿着没有芯管支撑的区域继续延伸，所以两者屈曲形状不同，且在面板发生鼓曲的位置芯管也出现不同程度的屈曲。从该有限元模型的最终破坏形态可以看出：不锈钢芯板L 形墙在压弯荷载作用下的最终破坏形态为偏心一侧墙肢上部的受压局部屈曲破坏，受拉侧未出现明显现象。

3 参数分析

以表2 模型LW4-1 各参数为基准，对本文有限元模型进行参数分析，确定影响不锈钢芯板L 形墙压弯承载力性能的关键参数。其中包括面板厚度tf、芯管壁厚tw、墙高l 以及偏心距e 的影响，各参数取值如表3 所示。

表3 各参数取值

3.1 面板厚度对抗弯承载力的影响(见图10)

图10 面板厚度对不锈钢芯板L 形墙压弯承载力的影响

从图10(a)可以看出，随着面板厚度的增加，构件的承载力和延性均有较大幅度的增加。当面板厚度为2.5 mm 时，构件的极限承载力只有797.61 kN，对应的位移为2.01 mm；当面板厚度为8 mm 时，构件的极限承载力为3905.59 kN，位移为13.24 mm。从图10(b)可以看出，构件无量纲承载力Nu/Afy与面板厚度tf近似为直线关系，构件的无量纲承载力随面板厚度的增大而增大。由图10 可知，面板是不锈钢芯板L 形墙的主要受力构件，而芯管的作用为增强两块面板之间的整体性、阻止面板过早发生局部屈曲。当面板厚度逐渐减小时，面板更容易产生局部屈曲，芯管亦不能发挥其作用，从而试件承载力也随之不断降低。随着偏心距的增大，这种变化趋势逐渐减缓，Nu/Afy-tf曲线越来越接近水平线，这是由于偏心距增大后，弯矩也随之增大，并逐渐起主导作用，导致构件受局部屈曲影响变小，构件延性有所增大。

3.2 芯管壁厚对抗弯承载力的影响(见图11)

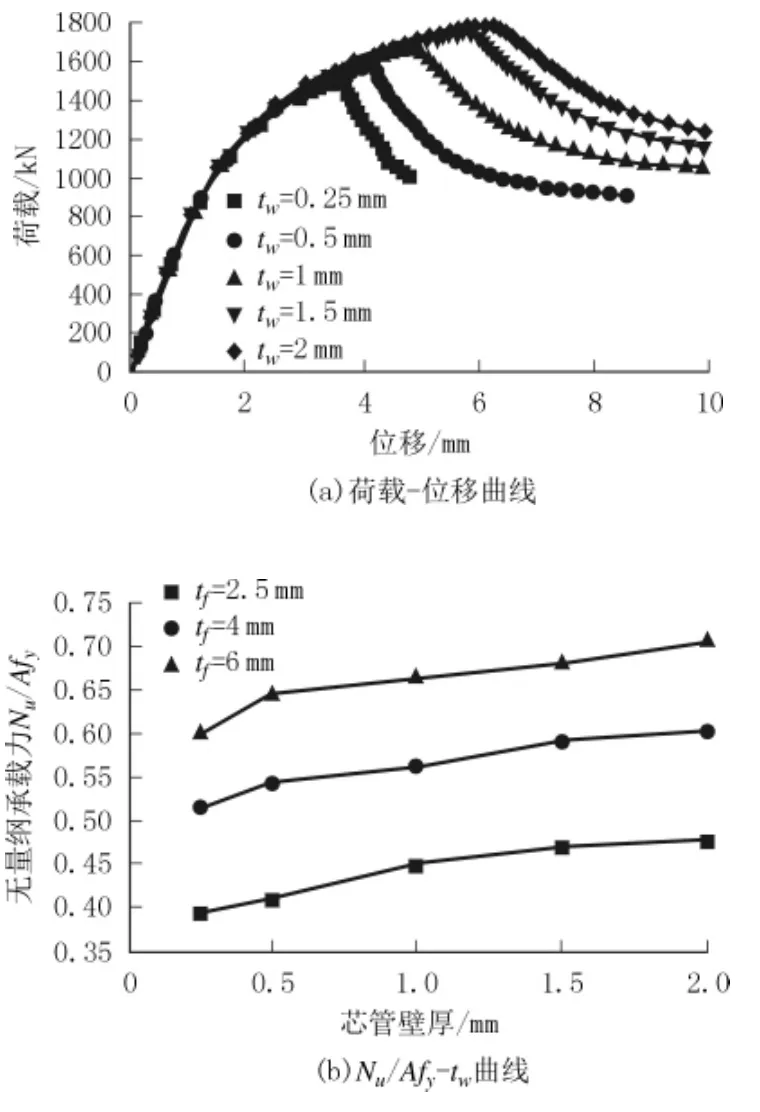
图11 芯管壁厚对不锈钢芯板L 形墙压弯承载力的影响

由图11(a)可以看出，增加芯管壁厚可以增强构件的延性和承载力，芯管壁厚从0.25 mm 增加到2 mm，构件极限承载力增大了17.7%。从图11(b)可以看出，构件的无量纲承载力随着芯管壁厚的增加而增加，增加芯管壁厚可以增强构件的整体性，并且能更好地防止面板过早屈曲，从而提高构件承载力和延性。

3.3 墙高对抗弯承载力的影响(见图12)

从图12(a)可以看出，不同墙高的构件极限承载力基本一致，但构件的延性随着墙高的增加而增大。从图12(b)可以看出，当面板厚度从2.5 mm 增大到8 mm 时，构件的无量纲承载力随墙高变化的关系曲线基本保持不变，这主要是因为构件的破坏均表现为局部屈曲破坏，与构件的高度影响不大。

图12 墙高对不锈钢芯板L 形墙压弯承载力的影响

3.4 偏心距对抗弯承载力的影响(见图13)

图13 偏心距对不锈钢芯板L 形墙压弯承载力的影响

从图13(a)可以看出，随着偏心距的增加构件的承载力减小，延性先减小后增大，这是因为加载时受压侧侧板首先屈服，随后塑性区不断向面板延伸，当偏心距小时，加载点离受压侧侧板较远，面板塑性区范围较大，从而构件的延性较好；偏心距较大时弯矩起主导作用，构件受局部屈曲影响较小，从而构件的延性有所增大。从图13(b)可以看出，对于不同厚度的面板，构件的无量纲承载力均随着偏心距的增加而减小，当偏心距较小时，构件的无量纲承载力减小迅速，偏心距较大时，无量纲承载力减小缓慢。且随着偏心距的增加，曲线上各点的分布也由分散到逐渐聚集。

4 N-M 曲线

由上述分析可知，面板厚度和偏心距是影响不锈钢芯板L 形墙压弯承载力的主要因素，故本节只选取两者分析其NM 曲线。弯矩M=N·e，当偏心距e 增大，弯矩增大，构件的承载力减小。面板厚度为2.5～8 mm 的N-M 曲线如图14 所示，图中Nu为有限元模型轴心受压极限承载力，Mu为纯弯状态下的极限弯矩。

图14 不锈钢芯板L 形墙单向压弯的N-M 曲线

从图14 可以看出，不锈钢芯板L 形墙单向压弯的N-M相关曲线在面板厚度不同时表现出不同的形式，当面板厚度较小时，不锈钢芯板L 形墙在压弯荷载作用下的N/Nu和M/Mu相关曲线近似为直线关系；随着面板厚度的增大，N-M 曲线形式逐渐转变为向外凸的曲线。

5 结 论

(1)本文提出的有限元模型能较好地模拟不锈钢芯板一字形墙在压弯荷载作用下的受力过程以及破坏形态。

(2)以不锈钢一字形墙有限元模型为基础，建立了不锈钢芯板L 形墙压弯模型，模拟了其在压弯荷作用下的受力过程，分析了构件的荷载-位移曲线和破坏形态，其破坏形式表现为受压侧的局部屈曲破坏。

(3)面板厚度和偏心距对构件压弯极限承载力的影响最大，芯管壁厚影响较小，构件高度基本无影响。增加面板厚度可以使芯管更好地发挥作用，提高构件的整体性并阻止面板过早发生屈曲，从而有效提高构件强度和延性；偏心距对不锈钢芯板L 形墙的压弯极限承载力和延性有较大影响，偏心距越大，弯矩在过程中越来越起主导作用。芯管壁厚的增加会在一定程度内提高构件的强度和延性。在1000～4000 mm 高度范围内，构件高度变化对极限承载力基本无影响，但增加构件高度能提高构件延性。

(4)不锈钢芯板L 形墙单向压弯的N-M 相关曲线在面板厚度不同时表现出不同的形式，当面板厚度较小时近似为直线，面板厚度较大时为向外凸的曲线。