古筝琴板的振动特性初探研究∗

嵇建书 裴永超 罗 敏 卢晓杰 郑梅生

（南京林业大学机械电子工程学院，江苏 南京 210037）

木材是木质乐器的重要组成部分，乐器质量等级主要由木材的材质决定，因此材料的选择对于乐器的制作至关重要。由于缺乏理论指导和科学手段，从业者在古筝等木质乐器的实际制作中，主要通过看、听、敲、掂等主观判断方法进行筛选，因此不仅乐器质量得不到保障，同时也造成木材的不合理利用与浪费。据行业相关统计，用于生产乐器共鸣板的原木出材率为10%～20%，出材率较低[1]。有研究表明，通过木材振动试验，分析各类木材的振动特性，将木材振动与声学联系起来，有助于发现木材振动特性与木质乐器质量之间的关系，从而帮助生产厂家筛选、分类材料，提高我国的乐器生产制造水平和木材的利用率[2-5]。为此，本文以古筝琴板为例，通过理论与试验分析相结合对木制乐器板材的振动特性进行研究，以期为古筝琴板及其他乐器木质板材的筛选与生产提供了一种有效的科学手段。

1 古筝琴板振动特性理论分析

木制乐器构造各异，但发声原理基本相同。以古筝为例，其结构如图1所示。木制乐器的初始振动由弦引起,琴弦振动导致面板振动，弦声通过面板、背板等形成的共鸣箱放大并传播出去,从而使人们享受到美妙的音乐[6]。

图1 古筝结构Fig. 1 Guzheng structure

我国民族乐器共振板的材料主要为泡桐与云杉属木材等[7-9]。共振面板是弹拨类乐器中的一个重要构件。琴板在振动时，既有弯曲振动，又有扭转振动。本文首先对琴板振动特性进行理论分析，以求出振动的固有频率理论解，为后续琴板振动试验提供理论依据。

1.1 弹性体的弯曲振动

匀质弹性体如矩形截面梁在xy平面内作横向弯曲振动，如图2所示。设其长度为l，横截面面积为A，ρ为每单位体积的质量，EI为弯曲刚度且为常量[10-11]。

图2 板的受力分析Fig. 2 Force analysis of board

从中取一个长度为dx的微段，上面有剪力Q(x,t)、弯矩M(x,t) ，在任何时间t,其横向位移可表示为y=(x,t)。忽略转动惯量和剪切变形的影响，由图3可知微段沿y方向力的平衡关系为：

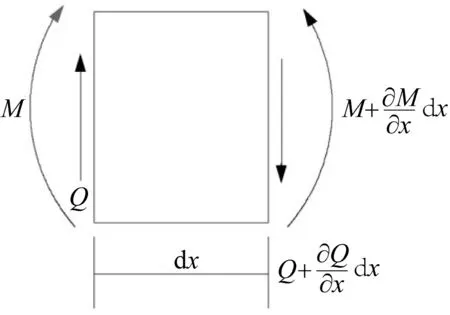
图3 板的微段受力分析Fig. 3 Force analysis of micro segment of board

解得其前5个值如表1所示。

表1 频率方程解Tab.1 Solution of frequency equation

最后，得到弹性体的弯曲振动固有频率计算公式如下[7]：

琴板属于弹性体，因为是各向异性材料，如以板的振动研究会使问题复杂化。因此尝试用公式（8）计算琴板的弯曲振动固有频率，并进行试验验证。将琴板的基本参数代入式（8），得到其弯曲振动固有频率f(Hz)近似计算公式如下[12]：

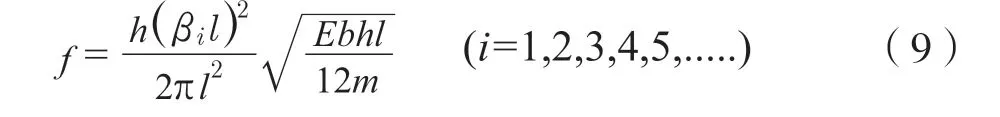
本试验用古筝琴板材质为泡桐，长l=1.7 m，宽b=0.355 m，厚h=0.01 m，质量m=1.62 kg，泊松比μ=0.4，弹性模量E=5.8×109Pa[9]。将具体数值代入公式（9），解得该琴板前五阶弯曲固有频率如表2所示。

表2 琴板弯曲振动固有频率Tab.2 Natural frequency of bending vibration of the board

1.2 弹性体的扭转振动

匀质弹性体如等直杆绕x轴作扭转振动，如图4所示。设杆的截面抗扭刚度、抗扭常数和剪切弹性模量分别为GJt(x)、Jt(x)和G[13]。

图4 杆的受力分析Fig. 4 Force analysis of the rod

图5 杆的微段受力分析Fig. 5 Force analysis of micro-segment of rod

假设杆扭转振动时，截面的翘曲可忽略。在平面内，截面将保持绕x轴作微摆动[14],取微段dx，x截面的角位移表示为θ(x,t)，微段对x轴的转动惯量Ip(x)，圆截面的极惯性矩为Jp。根据力矩平衡关系得[15]：

然后由边界条件解得β值及振型函数H(x) ,最后得到板的扭转振动固有频率计算公式如下：

与琴板弯曲振动同理，尝试用公式（14）计算琴板的扭转振动固有频率，并进行试验验证。将琴板的基本参数代入式（14），得到其扭转振动固有频率f(Hz)近似计算公式如下：

本文试验用古筝琴板的剪切弹性模量G=2.07×109Pa，其他数值同上。将具体数值代入公式（15），解得该琴板的扭转固有频率如表3所示。

表3 琴板扭转振动固有频率Tab.3 Natural frequency of torsional vibration of the board

1.3 有阻尼系统的衰减振动

自由振动物体的定义为，振动的振幅是恒定的，振动将无限期地继续下去。然而，实际的运动并非如此。自由振动的物体不但受到恢复力的作用，还受到阻力的作用，振幅会随着时间逐渐衰减，最终趋于零并停止振动，如图6所示[17]，其振动函数如下：

图6 阻尼振动运动图Fig. 6 Damping vibration motion diagram

通常把对振动过程的阻力称为阻尼，阻尼大小取决于物体的形状、尺寸及介质性质。琴板振动过程受阻尼的影响，呈现衰减振动。该分析结果将为试验结果分析中的时域图筛选提供一定的理论依据。

1.4 转动惯量、剪切变形对板振动的影响

当板的横截面尺寸与长度之比不是很小，或者在分析高阶振型时，整个板被节点平面分成若干比较短的小段，这时需要考虑转动惯量和剪切变形的影响[18]。该板的受力分析图如下：

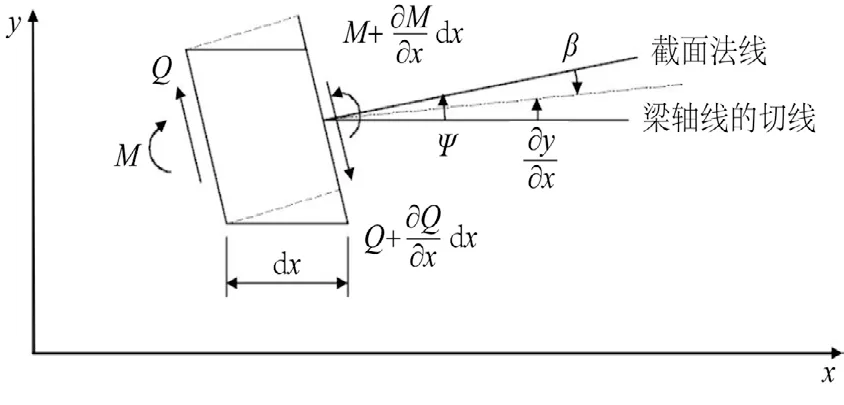
图7 铁木辛柯梁单元体受力图Fig. 7 Force diagram of Timoshenko beam element

取微单元dx，绘制剪切力和弯矩引起的变形。在剪力为零的条件下，单元体dx的中心线垂直于横截面。ψ为截面弯矩引起的夹角，β为剪力引起的剪切角，梁的轴线由弯矩和剪力引起的实际夹角为θ。通过建立动力方程、运动方程并求解，可得固有频率pi(Hz)计算公式如下：

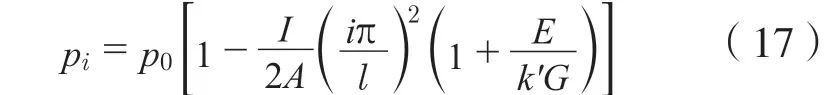
式（18）中p0(Hz)为不计转动惯量和剪切变形影响下的固有频率：

k为截面常数，矩形截面k=1.2，圆形截面k=1.11；EI为弯曲刚度，N·m2[10-11]；G为剪切弹性模量，Pa；ρ为每单位体积的质量，kg/m3；A为横截面面积，m2。

由式（18）可知，考虑了剪切变形和转动惯量后，系统的固有频率减小。由于系统的质量和刚度可以决定固有频率，剪切变形和转动惯量的影响不仅增加了系统的有效质量，而且降低了系统的有效刚度，导致固有频率下降。这种影响对高阶频率更为明显。

综上所述，琴板的实际固有频率要比理论计算的数值小。该分析结果将为试验结果分析中的时域图筛选提供一定的理论依据。

2 琴板振动特性试验台设计

2.1 设计目的与技术要求

设计并制作一种乐器木质板材振动特性测试装置，用于测试古筝、吉他等乐器的木质板材振动频率、弹性系数、阻尼系数等振动特性参数，为木质乐器生产厂家提供科学筛选板材的方法。

技术要求：1）板材悬吊后只限制其垂直向下自由移动，悬挂位置为手动操作，有限位装置； 2）支撑件位置可调，可以测试各类不同规格乐器板材及其他物体的振动特性；3）传感器等测试元件位置、角度可调，装夹方便；4）试验台易拆装。

2.2 试验台整体结构设计

琴板测试台由底板、立柱、挂棍、挡销、横梁、传感器、传感器夹、传感器支撑架等构成（图8）。底板用于支撑其他构件，其上开有横、竖两个方向的T型槽；两根立柱及横梁用于悬挂被测板材或其他物体，横梁与立柱之间用G型夹固定；立柱可沿底板的T型槽作纵向移动与固定，方便测量不同大小板材；两个支撑架外侧均设有挂棍与挡销，挡销设置在挂棍上方，同时挂棍上设有凹槽悬挂试验板材。传感器支撑架可沿底板的T型槽作横向移动与固定，方便传感器靠近被测物体以接收信号；磁性表座安于传感器支撑架上，并可快速固定；传感器装于磁性表座上，位置、角度均可调，装夹方便；整个试验台易拆装[19]。

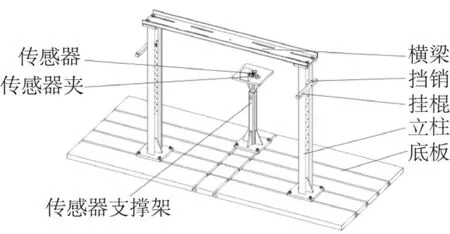
图8 试验台整体结构三维图Fig. 8 3D drawing of the overall structure of the test bench

3 琴板振动特性试验与结果分析

3.1 琴板自由振动频率测试试验

3.1.1 设备

自由振动试验设备均购于北京东方振动噪声研究所，包括振动分析软件DASP-V11、云智慧采集分析仪INV3062、声压传感器INV9206、力锤、电荷放大器、电脑、试验台等[20-22]。试验系统如图9所示。

图9 自由振动试验系统Fig.9 Free vibration test system

3.1.2 试验方法

利用试验台将琴板悬吊，吊线选在节线位置；将声压传感器的信号接收端固定于距离琴板中间3～5 cm处，接口端通过数据线与采集仪的2号端口连接；力锤通过电荷放大器与采集仪的1号端口连接；设置DASP软件的初始环境；进行锤击测试，锤击位置不固定，力锤对每个被测位置依次进行3次敲击，振动信号通过声压传感器传至采集仪，由采集仪将数据传输至振动分析系统进行处理。所有试验室温均为25 ℃，湿度为50%。

3.1.3 结果与分析[23-25]

经过振动分析系统处理后的时域图如图10所示，对应的频谱图如图11所示，数据列表如表4所示。

图10 时域图Fig. 10 Time domain diagram

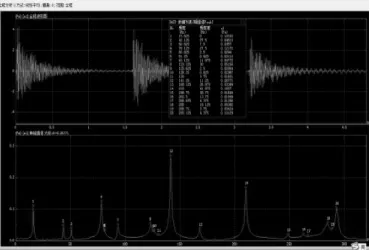
图11 频谱图Fig. 11 Spectrum diagram

表4 数据列表(幅值谱Peak)Tab.4 Data list (Amplitude spectrum Peak)

由图10、11可见，时域信号呈现典型的有阻尼衰减振动规律，频谱图的极值较为明显，试验结果较好。幅值谱的频率数据，部分为琴板的弯曲振动固有频率，部分为琴板扭转振动固有频率，其他为环境噪声产生的干扰频率。

3.2 琴板振动模态试验

模态试验是对古筝琴板振型进行试验分析。力锤锤击琴板时，3个加速度传感器将振动信号传递至采集仪，由其将信号传递至振动分析系统，采用模态与动力学分析模块进行模态分析。

3.2.1 弯曲振型

1）主要试验设备同3.1.1所列。

2）试验方法

首先用2块海绵支撑试验用琴板，与力锤连接的电荷放大器和3个加速度传感器依次分别接入采集仪的1至4号通道，3个加速度传感器分别置于选定的被测点，并用双面胶将其固定于琴板上；设置DASP软件内的信号采集模块，对锤击试验进行预试验，用力锤在每个被测点依次进行3次敲击，通过软件内的显示情况，判断预试验是否良好，若正常再进行正式试验。

3）结果与分析

试验得到的数据为时域信号。首先从时域图中选取一组信号良好的试验数据，利用振动分析系统中的模态与动力学分析模块对数据进行分析计算，操作步骤依次为数据导入、参数设置、频响函数计算、琴板结构生成、输入约束、脉冲响应函数、特征系统实现算法等，最后得到古筝琴板弯曲振动的前五阶固有频率、阻尼比（表5）及部分振型（图12、13）。

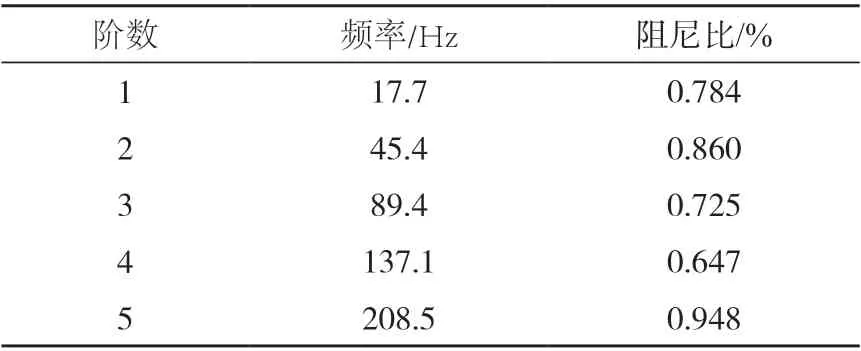
表5 弯曲振型固有频率和阻尼比Tab.5 Bending mode natural frequency and damping

图12 琴板弯曲二阶模态振型图Fig. 12 Second order modal diagram of the board bending

图13 琴板弯曲三阶模态振型图Fig. 13 Third order modal diagram of the board bending

二阶模态振型主要表现为琴板凹陷与凸起的往复运动。三阶模态振型主要表现为从左侧起凸起、凹陷、凸起以及凹陷、凸起、凹陷的交替运动。通过对比观察弯曲振型的固有频率和自由振动的频率大小，可以在表4中找到与表5相近的频率，再结合理论计算固有频率值，整理获得柱形图14。

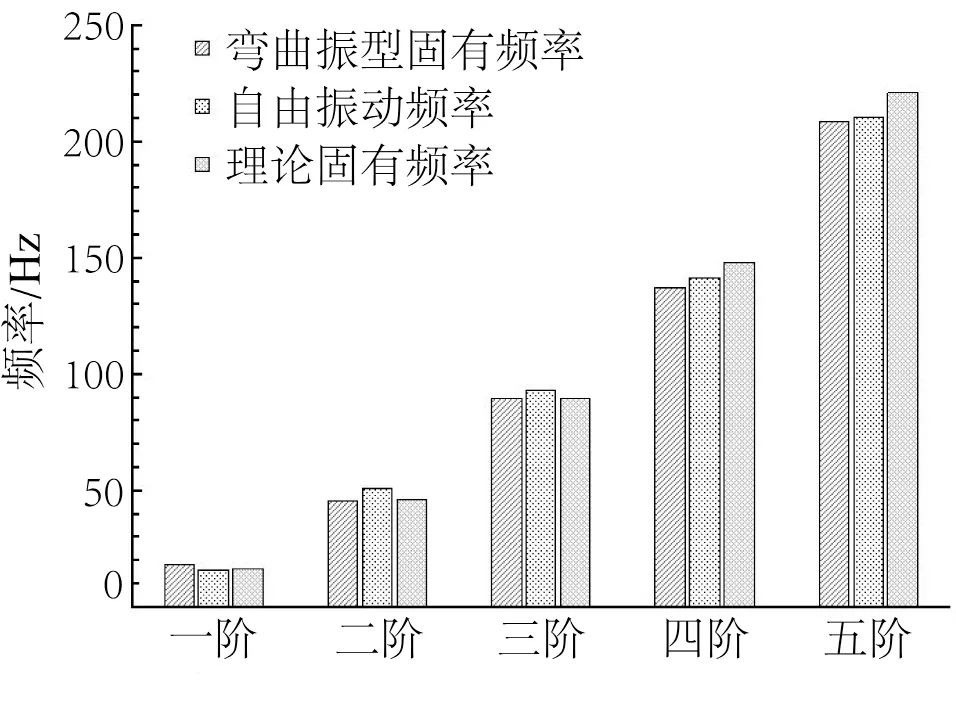
图14 弯曲振型固有频率与自由振动频率以及理论计算固有频率对比Fig.14 Comparison of natural frequency of bending mode and free vibration frequency and theoretical calculation natural frequency

对比图14中弯曲振型固有频率和自由振动频率以及理论计算所得出的前五阶频率，发现各阶频率值均相近，平均误差在5%以内，表明本文的研究结果可信度较高。

3.2.2 扭转振型

1）主要试验设备同3.1.1所列。

2）试验方法

首先进行DASP软件的设置，根据采样频率约为试验结果最高频率的5倍的试验要求，选用采样频率为2 048 Hz；试验采用4个通道，第1个为力锤通道，其他3个为加速度通道，设置每个通道的标定值；试验为锤击试验，触发次数为3次，采样点数为采样频率数值的一半，即1 024个，触发力设置为10 N；进行示波与零点平衡校准。然后将琴板两端放在备好的2块海绵上，避开一阶扭转的节线位置，将加速度传感器依次放在选定的被测点，并用双面胶将其固定；在琴板上依次选取7个激励点，力锤对每个激励点进行连续3次敲击，并采集试验信号。

3）结果与分析

加速度传感器将信号传递至分析仪进行处理，在振动分析系统中显示为时域信号，然后对时域信号进行筛选，选用模态与动力学分析模块依次进行分析，最后通过该模块的脉冲响应函数分析和特征系统实现算法得到琴板扭转振动的前五阶固有频率、阻尼比（表6）及部分振型。

表6 扭转振型固有频率和阻尼比Tab.6 Torsional mode natural frequency and damping ratio

图15 琴板扭转二阶模态振型图Fig. 15 Second-order mode shape of torsional vibration of the board

图16 琴板扭转三阶模态振型图Fig. 16 Third-order mode shape of torsional vibration of the board

通过对比观察扭转振型的固有频率和自由振动的频率大小，可以在表4中找到与表6相近的频率，再结合理论计算固有频率值，整理得到柱形图17。

对比图17中扭转振型固有频率和自由振动频率以及理论计算所得出的前五阶频率，发现各阶频率的值均相近，平均误差在6%以内，表明本研究具有较高的可信度。

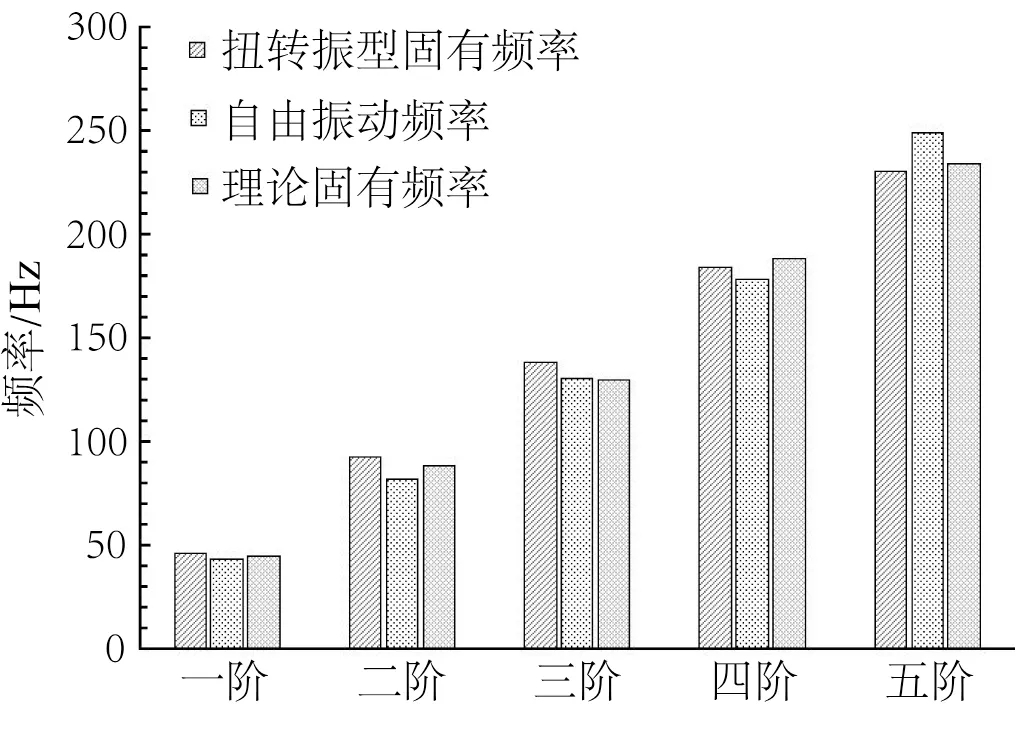
图17 扭转振型固有频率和自由振动频率以及理论计算固有频率对比Fig.17 Comparison of natural frequency of torsional mode and free vibration frequency and theoretical calculation natural frequency

4 结论

本文以古筝为例研究了乐器木质板材振动特性，对古筝琴板弯曲振动和扭转振动进行了理论分析和有阻尼的衰减振动分析，得到琴板的弯曲和扭转振动的前五阶固有频率理论计算值；设计并加工制作试验台；分别利用声压传感器和加速度传感器进行了琴板的自由振动频率测试与弯曲和扭转振动模态试验，获得琴板自由振动频率试验值及其弯曲和扭转振动前五阶固有频率试验值及振型；琴板振动的理论计算结果和2种试验结果对比表明：3个数值大小相近，平均误差分别在5%及6%以内，验证了本文试验方法的可行性和试验数据的可信度。

该研究成果对今后厂家筛选乐器木质板材具有一定的指导意义。今后还需深入研究乐器声学品质与木材振动性能的关系，并结合使用者对乐器成品的主观评价，综合分析，才能客观、科学地选取理想的乐器木质板材。