在数学建模中建立知识结构

孙凯

摘要：单元复习教学最重要的是找到合适的“大概念”（主题或线索）组织、串联因分课时学习而显得零散、无序、碎片化的单元内容，从而帮助学生建立单元知识结构，获得深度理解。《一元二次方程》单元复习课的教学，尝试引导学生经历完整的数学建模过程，在实际问题的提出和解决中，复习一元二次方程的概念与解法，理解一元二次方程产生与运用，体会一元二次方程是刻画现实世界数量关系的重要数学模型。这节课更深的教学立意有：追求理解的简约设计，指向迁移的能力提升。

关键词：单元复习;大概念;数学建模;知识结构;一元二次方程

单元复习，不是对分课时学习的单元内容的简单回顾和总结，而是一种居高临下的“再学习”。因此，单元复习教学最重要的不是设计新问题，通过问题解决再现有关知识，而是找到合适的“大概念”（主题或线索）组织、串联因分课时学习而显得零散、无序、碎片化的单元内容，从而帮助学生建立单元知识结构，获得深度理解。

人教版初中数学教材九年级上册第二十一章《一元二次方程》包括三节——《一元二次方程》《解一元二次方程》《实际问题与一元二次方程》，引导学生分课时学习一元二次方程的概念、表示、解法、根的判别式、根与系数的关系以及实际应用等知识。

设计这一单元的复习课时，笔者通过整体梳理，发现教材的编写思路是： 从现实情境问题引入，获得一元二次方程模型;类比一元一次方程概念，形成一元二次方程概念;接着，重点探究一元二次方程的求解方法，包括配方法、公式法、因式分解法等;最后，回到现实情境问题，运用一元二次方程解决。

由此，笔者提炼出“数学建模”这一“大概念”作为教学主题，尝试引导学生经历完整的数学建模过程，在实际问题的提出和解决中，复习一元二次方程的概念与解法，理解一元二次方程产生与运用，体会一元二次方程是刻画现实世界数量关系的重要数学模型，建立单元知识结构。

一、教学设计

（一）创设情境，提出问题

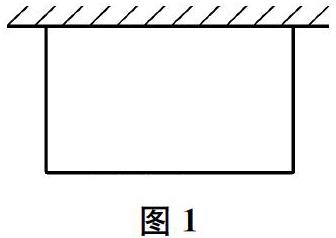
情境某农场要建立一个长方形的养鸡场，养鸡场的一边靠长为25 m的墙，另外三边用木栏围成，现有木栏长40 m。

问题1养鸡场面积能达到180 m2吗？

先提供一个现实情境，让学生试着提出问题，培养学生发现问题、提出问题的能力。在学生提出问题的过程中，如有必要，教师可以引导学生考虑现实需求，聚焦所围养鸡场的面积（直接关系到所养鸡的活动空间以及生存质量），从而给出预设的问题——问题1。

（二）数学抽象，建构模型

面对问题1，引导学生画出养鸡场图形（如图1），思考如何用数学语言表达现实问题中的数量及其关系，从而建构合适的数学模型，经历现实问题数学化的过程，培养应用意識。由长方形的面积，学生必然想到长方形的长和宽。由于长方形的长和宽均未知，学生必然想到设未知数为x（方程思想的表现）。这时，学生面临选择：设长还是设宽？对此，教师可以让学生尝试并比较，从运算方便性的角度发现，设宽为x，则长的表达式为40-2x，更简便一些。由此，学生根据问题中的数量关系，不难得到方程模型x（40-2x）=180和不等式组模型0<40-2x≤25。这时，教师可以追问：这是什么方程？由此，引导学生整理得到一元二次方程的一般形式x2-20x+90=0。

（三）求解模型，解决问题

面对一元二次方程模型x2-20x+90=0，引导学生思考求解方法，同步复习一元二次方程的解法。求解之后，引导学生检验。然后，引导学生利用数学模型的解，获得现实问题的解答。

这样，从现实问题出发，获得数学模型，在数学内部计算求解，再把数学模型的解回归现实检验修正，最终解决问题，使学生经历了完整的数学建模过程，明晰了一元二次方程的来龙去脉。

（四）变式探究

问题2养鸡场面积能达到200 m2吗？

问题3养鸡场面积能达到250 m2吗？

这两个变式问题引导学生再次经历完整的数学建模过程，获得巩固提升。同时，这两个现实问题所建构的一元二次方程模型分别有两个相等的实数根和无实数根，可以帮助学生复习一元二次方程根的不同情况。

（五）查漏补缺

问题4已知关于x的方程kx2-6x+9=0有两个不相等的实数根，则k的取值范围是_______________。

问题5已知x=2是方程x2-6x+m=0的一个根，则该方程的另一个根为__________________。

这两个问题是纯数学问题，目的是查漏补缺。问题4帮助学生复习根的判别式知识，强化对一元二次方程二次项系数不能为0的认识。问题5帮助学生复习根与系数的关系，强化对方程的解能使等式成立的认识;教学中，可以鼓励学生用不同的方法求解，并比较解法的优劣，从而充分体会根与系数的关系是由一元二次方程的解法得到的，知识之间是相互联系的。

（六）课堂小结

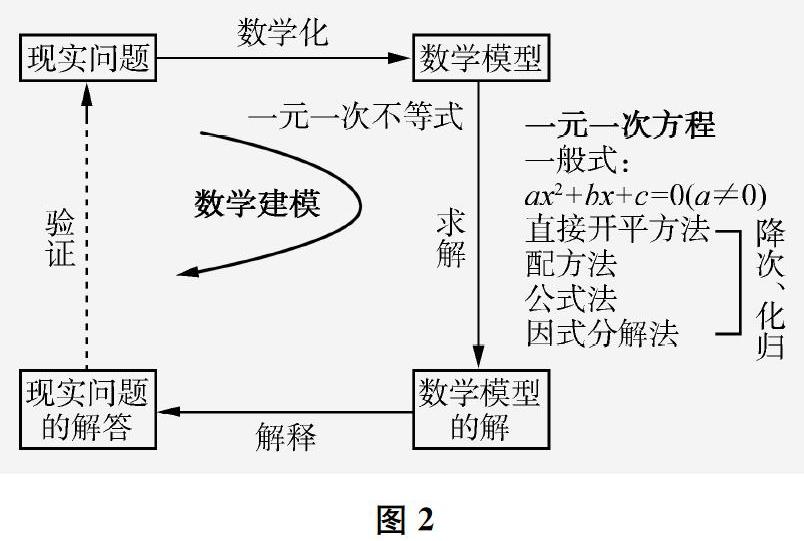
在学生经历了完整的数学建模过程（复习了本章的所有知识）的基础上，引导学生绘制本章知识（包括方法）结构图，最终呈现图2，从而发展学生的认知水平，提高学生的数学能力。

（七）当堂检测

练习1怎样用一条长为40 cm的绳子围成一个面积为75 cm2的矩形？能围成一个面积为101 cm2的矩形吗？如果能，说明围法;如果不能，说明理由。

练习2已知关于x的方程ax2-x-1=0有两个不相等的实数根，则a的取值范围是。

练习3已知x=3是方程x2-nx+6=0的一个根，则该方程的另一个根为。

练习1是对问题1—问题3学习情况的检测，练习2是对问题4学习情况的检测，练习3是对问题5学习情况的检测。当堂检查学习情况，即时反馈，提高复习效益。

二、教学立意

本节课的设计，除了整理把握教材的编写思路，利用问题驱动数学建模，在此基础上聚焦数学内部知识查漏补缺，帮助学生建立单元知识结构之外，还有更深的教学立意。

（一）追求理解的简约设计

美国学者林恩·埃里克森提出教学目标的三维模式（KUD）：知道（know）、做（do）、理解（understand）。其中，知道的是“事实”，做的是“技能”;而理解的是“概念”，是具有生活价值的反映专家思维方式的观念或论题。在这个三维模式中，理解是最核心的部分。就本单元的复习而言，让学生在知识层面知道一元二次方程的定义及一般形式、解法、根的判别式、根与系数的关系等，在技能层面正确求解一元二次方程及优化解法，固然重要，但更重要的是，帮助学生在宏观概念层面理解更具有一般性的数学建模过程，感受数学来源于生活且服务于生活。

（二）指向迁移的能力提升

有学者指出，迁移是教育的终极目标，学习只有在达到迁移水平时才算完成。所谓迁移，简而言之，就是把在一个情境中学到的东西运用到另一个情境。就本节课的教学而言，学生经历了完整的数学建模过程，也就掌握、积累了研究更多数学模型的一般方法、经验，从而具备了迁移的重要基础。比如，在后续《二次函数》单元的学习中，學生可以迁移《一元二次方程》单元的学习经验，从数学建模的视角，尝试自主建构单元知识（包括方法）结构（如图3），整体把握单元内容。

本文系江苏省教育科学“十三五”规划2020年度重点自筹课题“初中生数学建模能力培养与评价的实践研究”（编号：Bb/2020/02/104）、江苏省苏州市教育科学“十三五”规划2019年度课题“发展初中生数学建模素养的教学实践研究”（编号：192010343）的阶段性研究成果。

参考文献：

[1] 刘徽.“大概念”视角下的单元整体教学构型——兼论素养导向的课堂变革[J].教育研究，2020（6）.

[2] 约翰·D.布兰思福特，等.人是如何学习的——大脑、心理、经验及学校（扩展版）[M].程可拉，孙亚玲，王旭卿，译.上海：华东师范大学出版社，2013.

[3] Fisher，D.，et al.Visible Learning for Literacy，Grades K12：Implementing the Practices that Work Best to Accelerate Student Learning[M].Thousand Oaks，CA：Corwin，2016.