基于卷积神经网络的硬膜下和硬膜外血肿分割方法的一致性评价
田风选 常健博 陈亦豪 魏俊吉 冯铭 王任直 贺喜武
精确计算硬膜下血肿(SDH)和硬膜外血肿(EDH)体积具有重要临床意义[1]。既往研究发现,对于慢性硬膜下血肿,仅引流20%的出血即可有效帮助血肿吸收[2]。不同类型颅内出血有多种测量和计算方法,传统的手动分割方法系计算血肿体积的“金标准”,但该方法耗时费力;另一传统的方法多田公式,即长×宽×高/2(A×B×C/2),虽适用于脑实质出血、硬膜下血肿[3]和硬膜外血肿[4],但因硬膜下和硬膜外血肿形态并非均为对称的新月形或纺锤形,特别是许多慢性硬膜下血肿呈逗号样[5],故计算结果的准确性有待商榷。随着深度学习等计算机技术的进步,越来越多的学者开始尝试应用相关技术计算血肿体积,如Cho等[6]构建涵盖所有脑出血类型的血肿体积算法,准确度达80%、回归度为82%;国内常健博等[7]也发现,与多田公式等传统算法相比,卷积神经网络(CNN)与手动分割估算脑实质出血血肿体积的一致性更高。但迄今未见一种专门针对硬膜下和硬膜外血肿的算法,基于此,本研究拟提出一种基于卷积神经网络的算法分割(以下简称算法分割),并与多田公式、手动分割进行对比,以期探索一种精准、便捷的硬膜下和硬膜外血肿体积测量方法。
资料与方法
一、研究资料
1.资料来源 本研究所用影像学资料经中国颅内出血影像数据库(CICHID)授权[8],该数据库由中国医学科学院北京协和医院牵头,于2019年成立,截至2020年6月,该数据库共纳入20余所医疗中心计5000余例脑出血患者的头部CT影像资料。该数据库中的颅内出血主要以自发性脑实质出血为主,同时还包括脑室出血、硬膜下血肿、硬膜外血肿、蛛网膜下腔出血等类型,本研究选择硬膜下和硬膜外血肿的数据进行分析。
2.纳入与排除标准 (1)选择硬膜下和硬膜外血肿患者的头部CT影像。(2)均为术前或未行手术治疗时获得。(3)均为标准的DICOM格式,扫描参数及机器品牌不限。(4)年龄>18岁。(5)排除存在双侧硬膜下或硬膜外血肿的患者。
3.一般资料 根据上述纳入与排除标准,选择2017年1月至2019年6月共129例患者计352张(包含10 208层图片)CT影像,其中,硬膜下血肿患者有33例共104张CT扫描结果、硬膜外血肿患者96例共248张CT扫描结果。
二、研究方法
1.血肿体积估算方法 本研究纳入的352张CT影像均采用手动分割、算法分割、多田公式3种方法对血肿体积进行测量。(1)手动分割:采用Insight Toolkit SNAP开源软件(ITK⁃SNAP,https://itk.org/)[9],在横断面CT平扫影像上沿血肿边界进行勾画,输出血肿体积。手动分割时由一位研究员进行标注,由另一位研究员进行核实,标注边界有争议时与第三者讨论后决定。(2)多田公式:A×B×C/2是在ITK⁃SNAP开源软件辅助下,精确测量最大血肿面积层面最长径(A),以及该层面与最长径垂直的最长径(B),同时以实际层厚乘以出血层面数(C)[10]。由两位研究员分别独立完成A、B、C的精确测量,取平均值纳入最终统计。(3)算法分割:首先,为降低构建算法分割结果的过拟合风险,提高鲁棒性,对所纳入病例的CT影像进行五折交叉验证。即由计算机将CT影像随机均分为5组,每次选择4组作为训练集,余1组作为验证集,共进行5次训练,汇总5次模型在各自验证集的结果,以评估算法模型的性能。然后,将血肿手动分割数据作为卷积神经网络的输入数据,通过TensorFlow平台(https://tensorflow.google.cn)搭建三维卷积神经网络[9]。网络结构为3D U⁃Net,选择自适应矩估计(Adam)优化器作为迭代过程中的优化器,以权重交叉熵作为损失函数进行计算,以手动分割结果作为“金标准”,采用Dice相似性系数(DSC)作为分割精度标准进行训练。训练过程中实时检查损失函数和验证集上的分割精度,对收敛速度和趋势进行判断并调整网络参数,于训练集获得满意模型,在验证集获得算法分割结果。
2.血肿形态及边界对测量方法的影响 为进一步分析不同测量方法一致性检验存在差异的原因,本研究对不同测量方法的百分误差在不同血肿形态(对称与不对称)、血肿边界(模糊与清晰)中是否存在差异进行分析。其中,纺锤形血肿标记为对称,凹透镜形、逗号形等血肿标记为不对称;由标注员凭借经验根据血肿边界与脑组织之间CT值差距的大小判断血肿边界清晰或模糊。
3.统计分析方法 采用绝对差值和百分误差评估不同算法的准确性,百分误差的具体计算方法为︱V其他方法-V手动分割︱/V手动分割×100%;一致性检验采用Bland⁃Altman分析(均数-差值)、组内相关系数(ICC)表示,并采用PRISM GraphPad 8.0软件绘制Bland⁃Altman分析图。采用SPSS 20.0统计软件进行数据处理与分析,正态性检验采用Kolmogorov⁃Smirnov检验,呈非正态分布的计量资料以中位数和四分位数间距[M(P25,P75)]表示,采用Mann⁃WhitneyU检验。以P≤0.05为差异具有统计学意义。
结 果
经Kolmogorov⁃Smirnov检验,通过不同算法获得的血肿体积以及各种方法与手动分割的体积百分误差均为非正态分布资料(P=0.000),不同算法所得血肿体积和各种方法与手动分割的体积百分误差如表1所示,以手动分割结果为“金标准”,算法分割的百分误差小于多田公式,提示算法分割所得血肿体积更接近手动分割。

表1 不同算法测量的硬膜下和硬膜外血肿体积和百分误差[M(P25,P75)]Table 1. Subdural/epidural hemorrhage volumes and percentage error by different measurement methods[M(P25,P75)]
算法分割对手动分割差值的中位数(⁃4.51 ml)较多田公式对手动分割差值的中位数(8.39 ml)小,提示算法分割结果较多田公式更接近“金标准”。一致性分析显示,算法分割对手动分割差值的95%一致性界限(95%LoA)为⁃59.47~42.76 ml,差值范围为102.23 ml,而多田公式对手动分割差值的95%LoA为⁃15.15~37.50 ml,差值范围为52.65 ml,提示多田公式的波动范围较小;两种方法与手动分割的组内相关系数均较高(>0.75),提示两种算法与“金标准”均具有较好的一致性(表2,图1)。
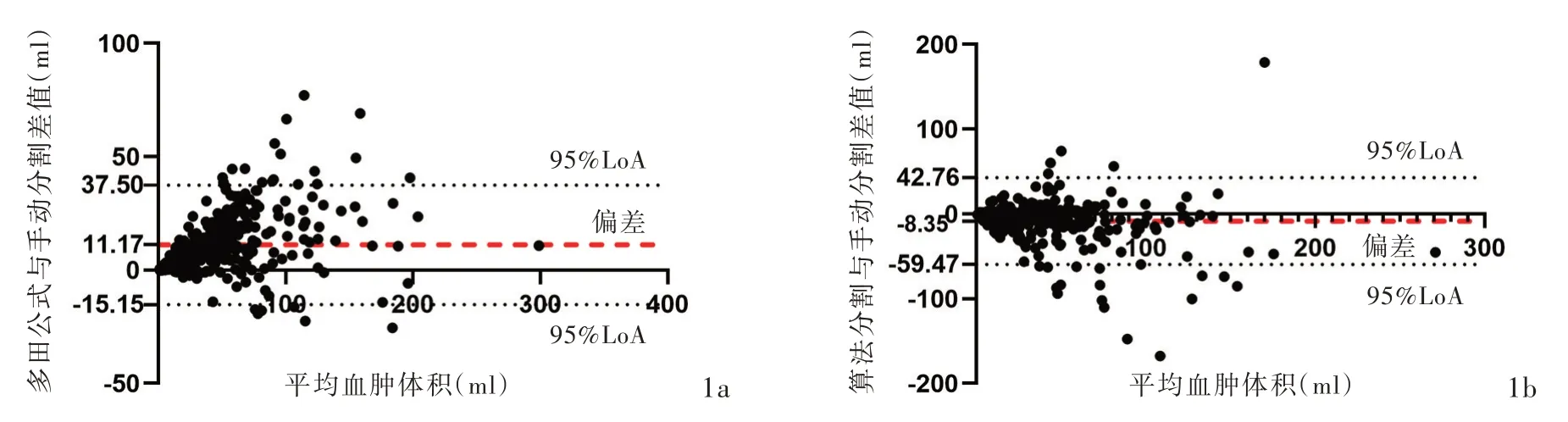
图1 Bland⁃Altman一致性检验 1a 多田公式对手动分割的95%LoA范围为⁃15.55~37.50 ml,约94.60%(333/352)的测值在95%LoA内 1b 算法分割对手动分割的95%LoA为⁃59.47~42.76 ml,约94.89%(334/352)的测值在95%LoA内Figure 1 Bland⁃Altman agreement test findings The 95%LoA of Tada formula vs.manual segmentation was⁃15.55-37.50 ml and the points inside 95%LoA was 94.60% (333/352,Panel 1a). The 95%LoA of algorithm segmentation vs.manual segmentation was⁃59.47-42.76 ml and the points inside 95%LoA was 94.89%(334/352,Panel 1b).

表2 不同测量方法的一致性检验(n=352)Table 2. Agreement test of different measurement methods(n=352)
不同血肿形态和边界在同一种血肿体积测量方法中的差异如表3所示,血肿对称与不对称之间算法分割的百分误差差异有统计学意义(P=0.000),提示算法分割在不对称血肿的百分误差更小;血肿边界(模糊与清晰)在算法分割和多田公式的百分误差均有统计学意义(P=0.000),其中算法分割在边界清晰的血肿百分误差更小,而多田公式在边界模糊的血肿中的百分误差更小。

表3 同一算法百分误差在不同血肿形态和边界中的比较[M(P25,P75),%]Table 3. Analysis of different hematoma shape and boundary in the same measurement method[M(P25,P75),%]
讨 论
本研究采用基于卷积神经网络的颅内血肿自动分割算法,可自动识别、分割头部CT平扫显示的硬膜下和硬膜外血肿,并计算血肿体积,以手动分割为“金标准”,分别对算法分割、多田公式进行一致性检验,结果显示,与多田公式相比,算法分割的百分误差最小,为23.62%;Bland⁃Altman分析显示,有94.89%(334/352)的测值在95%LoA内,与“金标准”的一致性良好;但算法分割的95%LoA波动范围更大,Mann⁃WhitneyU检验显示血肿形态和边界对算法分割的精确性有影响,算法分割测量形态不对称、边界清晰的血肿可能更佳。
多田公式的计算方法是由椭球体体积公式(4/3×π×0.5长×0.5宽×0.5高)简化而来,作为床旁简便、快捷的血肿体积估算工具,广泛应用于脑实质出血血肿的测量。也有学者探索其在硬膜下和硬膜外血肿中的应用。Petersen和Espersen[4]较早证实该公式可用于硬膜外血肿体积的估算,其平均误差为⁃2.7 ml(标准差为3.7 ml),但该项研究纳入标准严格限制为纺锤形硬膜外血肿,血肿量较小,故临床推广性较差。Gebel等[11]发现,多田公式与手动分割算法在急性硬膜下血肿中的相关性较高(r=0.842),但相关性低于脑实质出血(r=0.929)。Sucu等[1]验证多田公式在慢性硬膜下血肿中的应用,发现长径A和宽径B在血肿面积最大层面进行测量,优于在中间层面。但上述研究均存在一定局限性,首先是样本量较小,均<50例;其次,比较的是不同算法对同一整体的测量结果,但统计学指标并未采用一致性评价而采用相关系数(correlation coefficients)[12];最后,多田公式在慢性硬膜下血肿中高估血肿体积约10%[5]。与上述研究结果类似,本研究结果显示,多田公式可用于硬膜下和硬膜外血肿测量,其组内相关系数较高(0.974)。但本研究多田公式的百分误差较既往研究偏大(28.20%),平均高估出血量约8 ml,究其原因,可能是由于多田公式的误差随血肿体积的增加而增大[13]。
为弥补传统算法的不足,近年越来越多的研究应用神经网络相关算法用于血肿分割[6,14],其准确度(Dice值)高达80%[6]。本研究算法分割的百分误差较多田公式小(23.62%对28.20%),绝对误差更小(⁃4.51 ml对8.39 ml)。Bland⁃Altman图证实有94.89%(334/352)的测值在95%LoA内,显示与“金标准”的一致性良好,但其波动范围较大(⁃59.47~42.76 ml),其原因主要是算法分割在多中心数据集上泛化能力较差,在测试中存在极值案例,导致约5.11%(18/352)在95%LoA以外的误差远超过多田公式;其次,本研究采用五折交叉验证,即数据集随机分为5组轮流作为训练集和验证集,最终结果显示5种算法模型的平均能力,导致其95%LoA不仅反映算法分割与“金标准”之间的差异,而且反映不同算法模型之间的差异,导致其与多田公式相比,组内相关系数较低。
本研究还发现,无论是多田公式还是算法分割的准确性,均受血肿边界清晰度的影响。这可能是由于慢性硬膜下血肿的边界不清,在手工标注边界、测量径线时存在误差,即使双人背对背标注,仍存在较大的标注误差,难以确定实际出血量;同时这种标注误差也被引入算法分割训练中,使得算法分割的精确性降低。同时算法分割还受血肿形态的影响,其在不对称血肿中的百分误差优于对称血肿(17.37%对29.31%),而多田公式无论血肿形态其百分误差相近,约为30%,提示算法分割在形态不规则血肿中存在优势。
为了更好地把握病情、更精准地回答临床问题,如何简便快捷地计算颅内血肿体积,特别针对传统多田公式计算不准确的硬膜下和硬膜外血肿,是临床医师面临的挑战。脑实质出血的血肿体积被作为判断患者是否需行手术治疗的指征之一[15];但在硬膜下和硬膜外血肿中,由于多田公式存在较大误差,而手动分割又耗时费力,限制其在血肿体积与预后关系研究中的应用。简便、准确的硬膜下和硬膜外血肿体积测量工具的开发与应用与患者预后的关系,使探索血肿体积作为手术指征成为可能。随着人工智能(AI)技术在临床医学领域的深入应用,逐渐实现自动、精准和便捷的颅内血肿分割,是未来影像组学、手术模拟和手术导航等算法进一步研究的基础。
结 论
在硬膜下和硬膜外血肿中,与传统多田公式相比,采用卷积神经网络计算头部CT平扫图像中的血肿体积,其百分误差较小,与手动分割结果的一致性良好,在形态不对称、边界清晰的血肿中表现更好;但算法分割在少数病例中的误差较大,临床应用需进一步探索。
利益冲突 无

