竖管地表滴灌下风沙土稳定入渗率与湿润体估算模型

范严伟，王延祥，朱鹏程，杨志伟

竖管地表滴灌下风沙土稳定入渗率与湿润体估算模型

范严伟，王延祥，朱鹏程，杨志伟

（兰州理工大学能源与动力工程学院，兰州 730050）

为了量化解决竖管地表滴灌过程中滴头流量与竖管结构参数（竖管直径和竖管埋深）、土壤湿润体与植物根系的匹配问题，该研究通过12组竖管内积水（2 cm水头）入渗试验（9组率定，3组验证），测定不同竖管直径（8.8、10.6、12.6、14.2 cm）和竖管埋深（15、20、25 cm）条件下风沙土累积入渗量变化过程，并采用Philip入渗模型拟合。结果表明：竖管直径一定时，稳渗率随埋深的增大而减小，竖管埋深一定时，稳渗率随管径的增大而增大，稳渗率与竖管直径和竖管埋深之间符合幂函数关系（决定系数2>0.99），幂函数指数分别为2.01和-0.64。利用所建稳定入渗率估算式确定与竖管结构参数相匹配的滴头流量（保证竖管内无积水），设计9组竖管地表滴灌室内试验（7组率定，2组验证），观测不同滴头流量（0.9、1.2、1.5 L/h）、竖管直径（10.6、12.6、14.2 cm）和竖管埋深（15、20、25 cm）条件下风沙土湿润锋运移过程，并进行幂函数拟合，发现滴头流量对垂直向下湿润锋运移距离显著，滴头流量越大，垂直向下湿润锋运移距离越大，而水平方向和垂直向上湿润锋运移距离差异较小；在3个方向上湿润锋运移距离均随竖管直径的增大而减少；随竖管埋深增加，垂直向上和垂直向下湿润锋运移距离均有所减小，但水平方向湿润锋运移距离变化很小。确定了灌溉水到达竖管底孔所需时间计算式，在此基础上，构建了包括滴头流量、竖管直径、竖管埋深和灌水时间在内的竖管地表滴灌湿润体预测模型，验证所建模型的可靠性，平均绝对误差和均方根误差平均值分别为0.74和0.92 cm，纳什效率系数均大于0.91，说明预测效果良好。该研究所建稳定入渗率和湿润体预测模型对于竖管地表滴灌优化设计具有重要意义。

灌溉；入渗；模型；湿润体；稳定入渗率；竖管地表滴灌

0 引 言

风沙灾害是中国尤其是西北地区最为严重的生态环境问题[1-2]。植物固沙是防止风沙灾害和构建风沙区生态屏障的首选措施[3-4]。在沙漠化的土地上栽植固沙植物，存在幼苗成活率偏低（≤10%）、生长缓慢的瓶颈问题，而造成这一瓶颈的关键因素是土壤干旱和地表高温[5-8]。为提高固沙植物幼苗成活率，并使其健康生长，寻求一种可有效缓解固沙植物幼苗干旱高温复合胁迫的保育技术是非常有必要的。

近年来，管件防护造林技术逐渐应用于风沙治理和生态恢复工程中。该技术操作简单，其核心是使用环保管件将固沙植物幼苗套住，通过管件的防护，有效降低地表高温对幼苗的灼伤[9-10]。管件防护技术在地下水位相对较高或湿沙层相对丰富的荒漠区“发挥出色”，但在干旱沙漠区“表现不佳”，究其原因是其未从根本上解决根区土壤干旱问题。因此，以管件防护技术为载体，配套发展节水灌溉技术成为必然选择。就目前已经成熟应用的节水灌溉技术而言，滴灌应该是最高效的局部灌溉技术之一，在中国西北干旱区得到大面积推广应用[11-12]。基于此，笔者尝试将普通地表滴灌系统的滴头直接放入防护管件内，组成竖管地表滴灌系统。与无防护地表滴灌相比，竖管地表滴灌系统具有如下特点：1）有效降低地表高温、风沙流以及小动物啃食等对植物幼苗的胁迫伤害；2）改变传统地表湿润模式，降低表层土壤含水率，减少土壤蒸发损失；3）改善根区土壤水热状况，为植物幼苗创造相对适宜的微环境；4）调控根系向深层生长，提高其抗旱性和抗热性。

从方法上来说，竖管地表滴灌与白丹等[13]提出的竖管灌溉有本质的区别，竖管灌溉系统中干支毛管及竖管均埋入地下，其入渗形式为有压地下孔灌；竖管地表滴灌是将地表滴灌系统和防护管件有机结合，扩展了地表滴灌的技术优势，其入渗过程大致分为3个阶段：第1阶段，灌水初期，水滴入竖管，水分在管内水平扩散和垂直下渗，由于水分未到达管壁，近似“地表滴灌”；第2阶段，管内水分到达管壁，管内表层土壤饱和，在竖管的限制和引导下，管内水分从土壤表面垂直下渗至竖管孔底；第3阶段，管内水分到达管底，水分通过管孔向管外渗透，有水平扩散、向下入渗和向上吸升，近似“无压地下孔灌”。由此而见，竖管地表滴灌的突出特征是管壁对土壤水分运动的水平限制和垂向引导，其入渗特性与传统的地表/地下滴灌[14-16]以及适用于植树造林的蓄水坑灌[17]、涌泉根灌[18]、间接地下滴灌[19]、垂直线源灌[20]、深层坑渗灌[21]、垂直微润灌[22]等灌溉技术也完全不同。

目前，国内外还没有针对竖管地表滴灌相关研究工作，将其推广应用到植物固沙区尚缺乏完整的理论基础。从技术上而言，竖管地表滴灌存在竖管与滴灌的匹配问题，即当滴头与竖管组合时，滴头流量需小于等于竖管内临界积水条件下稳定入渗率（简称“临界积水稳定入渗率”），以满足管内水不淹苗的要求；从应用上而言，竖管地表滴灌存在湿润体与根系的匹配问题，土壤湿润体及其影响因素研究是合理设计竖管地表滴灌系统和提高水分利用效率的前提和基础。基于此，本文通过竖管内恒定水头（2 cm）积水入渗试验，并用Philip模型描述竖管积水入渗过程，确定临界积水稳定入渗率与竖管直径和竖管埋深的函数关系，量化解决滴头流量与竖管管件结构参数的匹配问题；在此基础上，试验研究不同影响因素（滴头流量、竖管直径和竖管埋深）组合下竖管地表滴灌过程中滴头流量、竖管管径和竖管埋深对湿润锋运移特征，并提出一种经验模型用来预测竖管地表滴灌湿润锋运移过程，从而为竖管地表滴灌系统中土壤湿润体与植物根系的有效匹配提供参考。

1 竖管地表灌溉系统

竖管地表滴灌是为缓解固沙植物幼苗干旱高温复合胁迫而提出的一种节水控温保育技术。如图1所示，该项技术实际应用时，先将固沙植物幼苗移入沙土中，再从幼苗头部套入竖管，并插入沙土中一定深度，最后将滴头放入竖管。灌溉时，滴头将水注入竖管，水穿过管内土壤到达管底，并通过管底孔向根区土壤入渗。

1.固沙植物幼苗 2.竖管 3.滴头 4.支管 5.毛管接头 6.毛管 7.水 8.风沙土 9.湿润体

1.Sand fixing plant seedlings 2.Vertical pipe 3.Emitter 4.Branch pipe 5.Capillary joints 6.Capillary 7.Water 8.Aeolian sandy soil 9.Wetting pattern

图1 竖管地表滴灌系统

Fig.1 Vertical pipe surface drip irrigation system

2 材料与方法

2.1 试验材料

试验于2020年6－8月在兰州理工大学水利水电工程实验室进行。土样取自民勤荒漠-绿洲过渡带，土壤类型为风沙土，取土深度为0～30 cm，土样经风干、过筛后待用。室内测定其干容重γ=1.52 g/cm3，初始含水率θ=0.031 cm3/cm3，饱和含水率θ=0.434 cm3/cm3，饱和导水率K=0.218 cm/min。试验装置由试验土箱和供水系统组成，如图2所示。

土箱采用10 mm的有机玻璃板粘制，内部尺寸长宽高均60 cm。土箱底部留有多个通气孔（孔径2 mm），以防气阻发生。供水系统包括蓄水桶、进水管、蠕动泵、出水管和1/2竖管5部分，其中竖管由有机玻璃管切割而成。试验前，将供试土样按设定的初始含水率（0.031 cm3/cm3）加水，均匀混合后，用塑料薄膜密封静置1 d。待土壤水分分布均匀后，按设定容重（1.54 g/cm3）、层厚（5 cm）装入土箱，层间刮毛。待装土到一定高度后，将1/2竖管按照设定试验方案预埋于土箱边壁正中心位置处，竖管内也需根据设定容重装土，装土高度与地表水平。装土完毕后每个处理重复3次。

2.2 试验方案

2.2.1 竖管积水入渗试验

为满足竖管内水不淹苗的要求，滴头与竖管组合时，需滴头流量小于等于临界积水稳定入渗率。为此，利用马氏瓶供水，通过可变高度铁架调节至2 cm恒定水头，开展竖管内积水入渗试验，研究竖管直径和埋深对竖管积水风沙土入渗特性。竖管直径取4个水平，埋深根据固沙植物幼苗根长取3个水平，按照全组合布置12组试验方案，试验方案见表1，其中方案10、11、12为验证试验。每组试验方案入渗时间均为150 min，观测时间间隔按照先密后疏的原则进行，记录不同时刻马氏瓶水位变化值，试验结束后，将对应时刻的马氏瓶水位变化值与马氏瓶的横截面积（内径）相乘计算得累积渗量。

2.2.2 竖管地表滴灌入渗试验

根据已建立的稳定入渗率估算模型，考虑滴头流量、竖管直径和埋深3个影响因素，且保证竖管管内在各因素组合下不存在积水，每个因素取3个水平，其中滴头流量分别为50%Q（稳定入渗率）、70%Q和90% Q，蠕动泵以设定恒定流量向竖管供水，进行竖管地表滴灌试验。试验方案见表2，其中方案8、9为验证试验。

试验过程中，用马克笔在土箱外壁标记设定时刻土壤湿润锋轮廓线，入渗结束后（2.5 h），用钢尺量测湿润锋3个方向（水平、垂直向上和垂直向下）的运移距离。其中：垂直向下方向以竖管孔底中心为原点，水平和垂直向上方向以竖管孔底边壁为原点，量读数据，均取正值。

表1 竖管内积水入渗试验方案

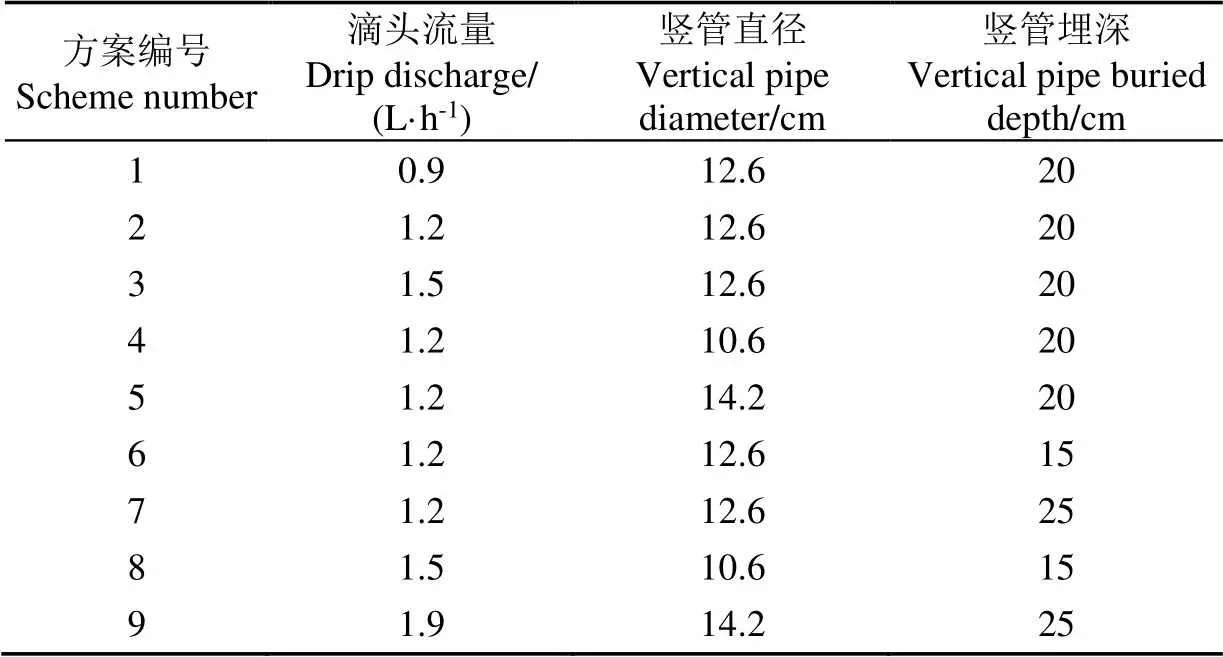
表2 竖管地表滴灌试验方案

2.3 临界积水稳定入渗率描述

白丹等[13,19-20]研究表明，恒定积水条件下空间三维入渗过程可采用Philip入渗模型描述。为此，本研究选取Philip入渗模型来定量分析竖管内积水试验累积入渗量随时间的变化过程。Philip入渗模型[23]表达式为

0.5（1）

式中为累积入渗量，L；为吸渗率，L/h0.5；为稳渗率，L/h；为入渗时间，h。

2.4 数据处理与分析

采用Excel 2010和Origin 2018软件进行数据处理，对不同因素不同水平处理下的实测数据进行单因素对比分析；借助指标平均绝对误差、均方根误差和纳什效率系数对模型误差进行统计分析[24]。统计参数计算方程如下：

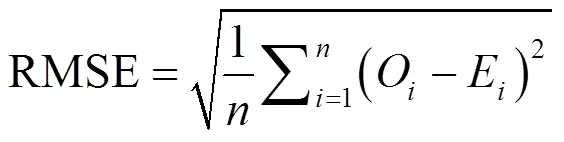
式中MAE代表平均绝对误差；代表数据总个数；O和E分别代表第个观测值和估算值；RMSE和NSE分别代表均方根误差和纳什效率系数；O代表观测值的平均值。MAE和RMSE的数值越靠近0，NSE的数值越接近1，表示估算值相对于观测值偏差越小，两者吻合度越高。

3 结果与分析

3.1 不同影响因素对累积入渗量的影响

根据竖管内积水（2 cm恒定水头）入渗试验，得到每组方案下累积入渗量随时间的变化过程，如图3所示。

对比图3发现，竖管直径（即管径）一定时，同一时刻下累积入渗量随竖管埋深的增大而减小，但变化幅度不大。如灌水结束（2.5 h）时，管径为8.8 cm竖管，埋深20、25 cm比埋深15 cm累积入渗量分别低0.12、0.43 L；在管径为10.6 cm情况下，竖管20、25 cm埋深比15 cm埋深分别低0.40、0.83 L，而管径12.6 cm的竖管深埋（20、25 cm）比浅埋（15 cm）分别低0.67、0.94 L。分析原因可能为竖管埋深增大，延长了竖管内土壤水分渗流至竖管孔底路径长度，降低了竖管内水力梯度，从而导致累积入渗量减小。竖管埋深一定时，同一时刻下累积入渗量随竖管直径的增大而增大，其影响相对较大。灌水结束时，管径为8.8、10.6和12.6 cm的竖管在埋深15 cm的条件下，累积入渗量分别为2.43、3.88和5.24 L；而埋深20 cm时，3种管径（8.8、10.6和12.6 cm）累积入渗量分别为2.31、3.48和4.57 L，埋深25 cm时，3种管径累积入渗量分别为2.00、3.05和4.30 L。这可能由于竖管管底作为土壤水分的入渗界面，竖管直径越大，水分进入土壤的通道就越多，使整个竖管孔底入渗界面上的入渗水量随之增大。

3.2 临界积水稳定入渗率模型分析

采用Philip入渗模型对不同竖管直径和竖管埋深组合下试验数据进行拟合，得到吸渗率和稳渗率参数值，如表3所示。

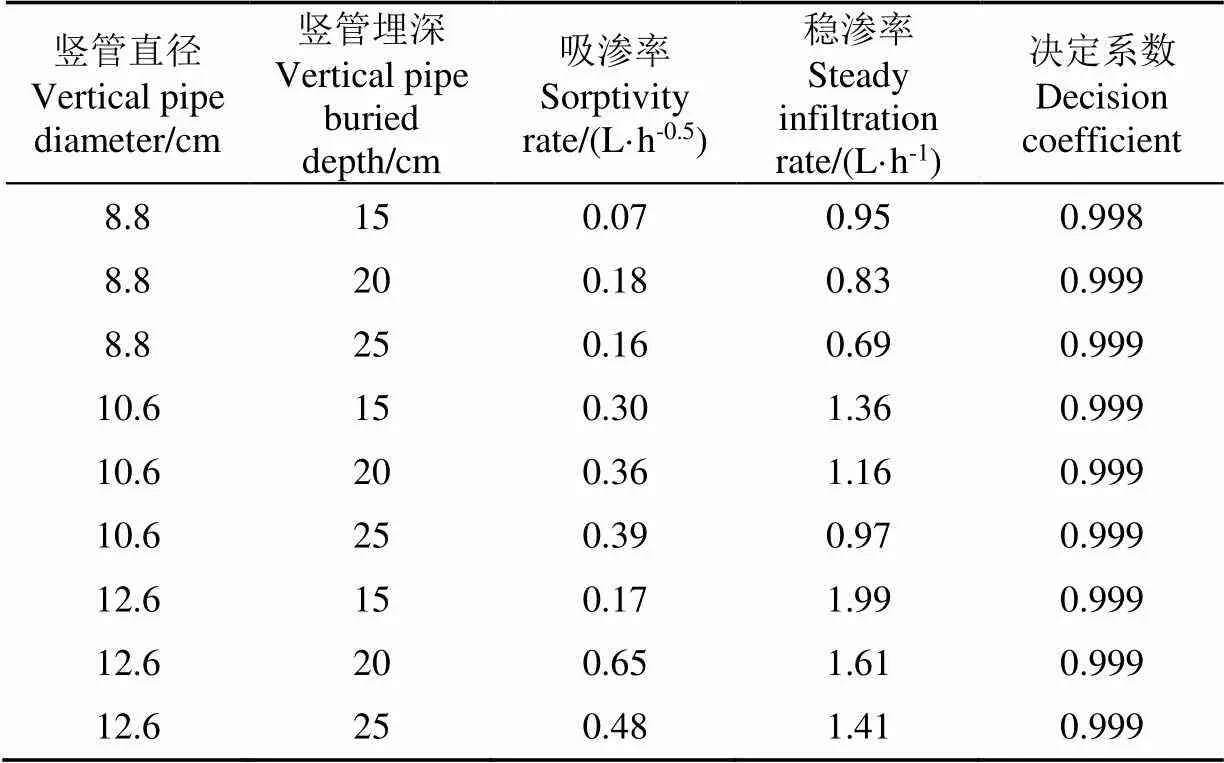
表3 Philip入渗模型参数拟合

表3中决定系数2均大于0.99，说明Philip模型能够充分且准确地反映竖管内积水情况下累积入渗量与时间的关系。竖管直径和竖管埋深的变化，均对稳渗率有不同程度的影响，而对吸渗率的影响没有规律。竖管直径一定时，稳渗率随埋深的增大而减小，竖管埋深一定时，稳渗率随管径的增大而增大。进一步分析发现，的数值远小于值，结合Philip模型表达式可知，参数项的时间变量为0.5，而参数项的时间变量为，随着入渗时间（）的延长，会进一步加剧大于0.5现象，表现为对累积入渗量的作用逐渐减弱，而对其影响逐渐增大，并成为主导影响因素。基于此，可用稳渗率近似表征稳定入渗率（Q）。构建Q与竖管直径（）和竖管埋深（）的经验模型：

Q=kDB（5）

式中Q为稳定入渗率，L/h；为竖管直径，cm；为竖埋深，cm；为入渗系数；和为拟合指数。

采用式（5），拟合表1中试验方案1～9的试验数据，获得0.072，=2.01，=-0.64，进而可得Q表达式为

Q=0.0722.01-0.64（2=0.997，RMSE=0.312 L/h） （6）

采用表1中方案10、11和12，对式（6）进行验证，结果见表4。

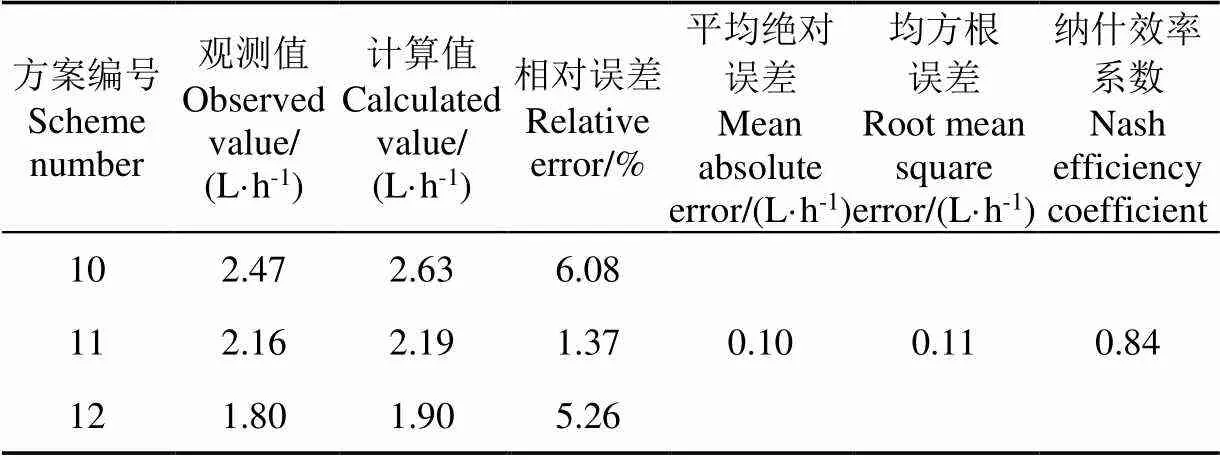
表4 稳定入渗率经验模型验证

表4可见，计算值与实测值的相对误差介于1.37%～6.08%，平均绝对误差和均方根误差分别为0.10和0.11 L/h（接近于0），纳什效率系数为0.84（接近于1），说明计算值与实测值一致性良好，式（3）能够预测不同管径和埋深组合下的稳定入渗率。

3.3 竖管地表滴灌土壤水分运动特征

3.3.1 滴头流量对湿润锋运移的影响

从7组试验方案中，不同和影响因素组合下对进行单因素分析时，选取表2中试验方案1、2和3的观测数据进行整理，绘制不同滴头流量情况下湿润锋运移距离随时间的变化曲线，如图4所示。

注：竖管直径为12.6 cm，竖管埋深为20 cm。

Note: The vertical pipe diameter is 12.6 cm and the vertical pipe buried depth is 20 cm.

图4 3种滴头流量情况下湿润锋运移距离与时间的关系

Fig.4 Wetting front transport distance as a function of time for three different emitter discharge rates

由图4可见，在竖管直径和埋深一定时，滴头流量对垂直向下湿润锋运移距离影响显著，而水平方向和垂直向上湿润锋运移距离影响相对较小。滴头流量越大，垂直向下湿润锋运移距离越大，灌水结束（2.5 h）时，3种滴头流量（0.9、1.2和1.5 L/h）所对应的湿润锋运移距离分别为24.5、29.3、32.4 cm，1.2和1.5 L/h滴头流量比0.9 L/h滴头流量分别增大了4.8和7.9 cm；在水平方向，3种滴头流量所对应的湿润锋运移距离分别为13.4、14.7、15.0 cm，1.2和1.5 L/h滴头流量比0.9 L/h滴头流量仅增大了1.3和1.6 cm；在垂直向上方向，3种滴头流量所对应的湿润锋运移距离分别为7.0、8.0、7.8 cm，1.2和1.5 L/h滴头流量比0.9 L/h滴头流量仅增大了1.0和0.9 cm。

3.3.2 竖管直径对湿润锋运移的影响

从7组试验方案中，不同和影响因素组合下对进行单因素分析时，整理表2中试验方案2、4和5的观测数据，得到不同竖管直径情况下湿润锋运移距离随时间的变化曲线，如图5所示。

由图5可见，相同滴头流量和竖管埋深条件下，随着竖管直径增大，湿润锋在3个方向（垂直向下、水平、垂直向上）上的运移距离均呈减小趋势。灌水结束（2.5 h）时，对于小管径（10.6 cm）竖管，湿润锋在3个方向上的运移距离均达到最大值，分别为30.8（向下）、15.0（水平）、8.8 cm（向上），当管径增大到12.6和14.2 cm时，湿润锋运移距离在垂直向下方向上分别减小了1.5和3.7 cm，水平方向上减小了0.3和0.8 cm，垂直向上方向上减小了0.8和1.1 cm。

注：滴头流量为1.2 L·h-1，竖管埋深为20 cm。

Note: The drip discharge is 1.2 L·h-1and the vertical pipe buried depth is 20 cm.

图5 3种竖管直径情况下湿润锋运移距离与时间的关系

Fig.5 Wetting front transport distance as a function of time for three different vertical pipe diameters

3.3.3 竖管埋深对湿润锋运移的影响

从7组试验方案中，不同和影响因素组合下对进行单因素时，分析表2中试验方案2、4和5的观测数据，分析表2中试验方案2、6和7的观测数据，获得不同竖管埋深情况下湿润锋运移距离随时间的变化曲线，如图6所示。

注：滴头流量为1.2 L·h-1，竖管直径为12.6 cm。

Note: The drip discharge is 1.2 L·h-1and the vertical pipe diameter is 12.6 cm.

图6 3种竖管埋深情况下湿润锋运移距离与时间的关系

Fig.6 Wetting front transport distance as a function of time for three vertical pipe buried depths

由图6可见，在滴头流量和竖管直径一定时，竖管埋深对垂直向下湿润锋运移距离影响显著，竖管埋深越大，同一时刻垂直向下湿润锋运移距离越小，而水平方向和垂直向上湿润锋运移距离差异较小，规律不明显。灌水结束（2.5 h）时，在垂直向下方向上，3种竖管埋深（15、20和25 cm）所对应的湿润锋运移距离分别为31.0、29.3、27.2 cm，20和25 cm竖管埋深比15 cm竖管埋深分别减少了1.7和3.8 cm；在水平方向上，3种竖管埋深所对应的湿润锋运移距离分别为14.6、14.7、14.5cm，最大值和最小值仅相差0.2 cm；在垂直向上方向上，3种竖管埋深所对应的湿润锋运移距离影响不显著，竖管20和25 cm埋深比15 cm埋深分别减少了0.7和0.8 cm。

3.4 竖管地表滴灌湿润体尺寸估算模型建立与验证

点源入渗的水平和垂直湿润锋运移距离与各影响因素间存在幂函数关系，利用幂函数能够精确反映点源入渗湿润锋的发展过程[25-26]。采用多元线性回归分析发现竖管地表滴灌模式下土壤湿润锋运移距离与滴头流量、竖管直径、竖管埋深和灌水时间同样符合幂函数关系。通过前面分析，竖管底孔外围湿润体发展的计时起点应为灌溉水到达竖管底孔时刻。因此，首先应确定灌溉水到达竖管底孔所需时间0。已知蠕动泵流量、1/2竖管内土体体积量、竖管内土体平均体积含水率θ、竖管内土体初始体积含水率θ，依据土壤水分平衡原理，得到时间0计算式

0=0.008 7(θ−θ)/（2=0.860） （7）

式中0为灌溉水到达竖管底孔所需时间，h；为1/2竖管内土体体积量，cm3；θ为竖管内土体平均体积含水率，cm3/cm3；θ为竖管内土体初始体积含水率，cm3/cm3；为滴头流量（蠕动泵流量），L/h。

对式（7）求解，得表2中方案1～7的0计算值，并与实测值列于表5。

表5 水分入渗到达竖管底部所需时间

由表5可见，计算值与实测值是非常接近的，仅相差0.01～0.06 h，而该差值相对于整个灌溉历时（通常4～5 h）是完全可以忽略的。因此，采用式（7）预估灌溉水到达竖管底孔所需时间是可行的。

进一步地，采用多元回归法，构建湿润锋运移距离与滴头流量、竖管直径、竖管埋深和灌水时间的经验模型：

Z=KQDB(−0)（8）

式中Z为湿润锋不同方向运移距离，cm；=1、2或3，其中1代表垂直向下湿润锋运移距离，2代表水平向湿润锋运移距离，3代表垂直向上湿润锋运移距离；K、a、b、c和d为待定参数。

采用式（8），拟合表2中试验方案1～7的试验数据，获得K、a、b、c和d值，进而得到Z计算式：

157.780.42-0.23-0.18(−0)0.53

（2=0.991，RMSE=1.027 cm） （9）

245.240.17-0.63-0.01(−0)0.60

（2=0.993，RMSE=0.732 cm） （10）

3=164.690.08−0.90−0.41(−0)0.59

（2=0.996，RMSE=0.924 cm） （11）

为评价竖管地表滴灌湿润锋预测模型的可靠性，采用表2第8、9组试验数据进行验证。将经验预测模型的计算值与实测值进行对比分析，如图7所示。

由图7可见，不同方向湿润锋运移距离实测值与模型计算值趋势一致，进一步利用检验计算得到3个方向的值，值均大于0.05，说明3个方向上湿润锋运移距离的模型计算值与试验观测值均无显著性差异。借助统计指标平均绝对误差、均方根误差和纳什效率系数对模型进行误差分析（表6），结果显示平均绝对误差介于0.28～1.07 cm之间，平均值为0.74 cm，均方根误差介于0.19～1.68 cm之间，平均值为0.92 cm，纳什效率系数均大于0.91，模型预测效果良好。

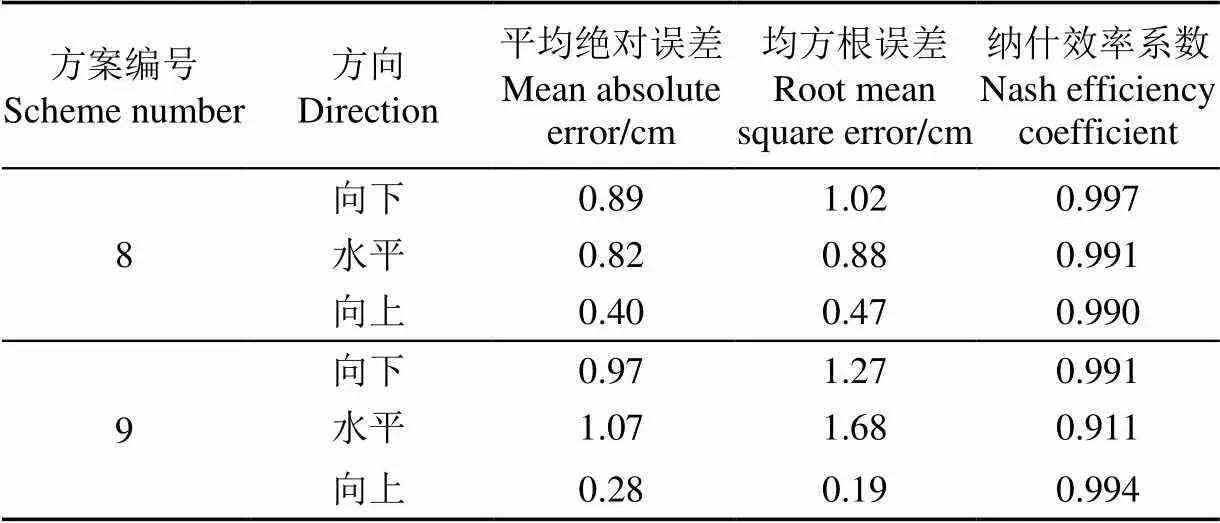
表6 验证试验湿润锋运移距离模型计算值与实测值比较

4 讨 论

竖管地表滴灌相对于普通地表或地下滴灌，增加了竖管直径和竖管埋深2个管件参数，产生了管壁对土壤水分运动的水平限制和垂向引导。竖管地表滴灌土壤水分入渗可划分为3个阶段：第1阶段，水被滴入竖管，“地表滴灌”形成，水分快速扩散，管内土壤表层饱和，该阶段湿润范围小，发展历时短，可忽略不计；第2阶段，在竖管的限制和引导下，管内水开始垂直下渗，直至水分到达竖管底孔，该阶段研究意义在于灌溉水到达竖管底孔所需时间的估算，以便能够更精准地预测竖管底孔外围湿润体尺寸大小；第3阶段，水分到达竖管底孔，侧渗现象发生，土壤水分运动转化为“无压地下孔灌”，该阶段是认识植物根区土壤水分运动的关键，也是设计竖管地表滴灌系统的基础。

滴头流量是竖管地表滴灌系统的关键设计参数，其数值要与竖管结构参数相匹配，以满足竖管内不积水的要求。另外，滴头流量对竖管地表滴灌土壤湿润体尺寸有较大影响。分析原因为：相同管径和埋深情况下，滴头流量决定灌溉水分到达竖管底孔的时间和单位时间内进入土体的水量。表现为：滴头流量越大，灌溉水分到达竖管底孔的历时越短，单位时间内进入土体的水量越多，导致竖管底孔外围湿润体体积越大。对沙性土，现有地表滴灌研究表明，当灌水时间一定，随着滴头流量的增大，湿润锋水平和垂直方向湿润锋运移距离随之增大[27]；也有研究表明，滴头流量的大小对土壤湿润体的横向尺寸影响较小，对湿润体纵向尺寸（深度）影响较大[28-29]。需要说明的是，沙性土孔隙率大、重力作用明显，竖管地表滴灌过程中，容易造成水分深层渗漏和横向亏缺。因此，根据植物根系的分布情况，选择合适的滴头流量，提高灌溉水利用效率。

竖管直径和竖管埋深属于竖管地表滴灌管件结构参数，对土壤湿润体尺寸有一定影响。从植物生长和经济角度考虑，竖管直径应大于或等于固沙植物幼苗冠幅，竖管埋深至少等于固沙植物幼苗根长。竖管地表滴灌模式下，在3个方向上湿润锋运移距离均随竖管直径的增大而减少，在垂直向上和垂直向上方向上湿润锋运移距离随竖管埋深的增大而略有减小，但水平方向上湿润锋运移距离变化很小。这一结论与白丹等[30-31]研究结果恰好相反。究其原因是文献[30-31]中竖管底孔处水土交界面存在压力势（压力水头），属于充分供水条件下的地下孔灌，管径越大，底孔渗水面越大，埋深越深，压力水头越高，导致单位时间内进入土体的水量越多，竖管底孔外围湿润体体积越大。竖管地表滴灌入渗过程中，管内无积水，竖管底孔处水土交界面土壤未饱和，不存在压力势，属于非充分供水条件下的地下孔灌，管径越大，埋深越深，竖管内土体体积越大，进而管内需要被水填充的孔隙体积越大。因此，滴头流量一定时，竖管直径和埋深决定灌溉水分到达竖管底孔的时间。表现为：管径和埋深越大，灌溉水分到达竖管底孔的历时越长，导致竖管底孔外围湿润锋运移的滞后现象。

文中所建湿润体预测模型是关于滴头流量、管件结构参数和滴灌时间的函数，模型简单且预测精度高，可方便设计者确定合理的竖管地表滴灌参数以及运管人员进行快速的现场评估。需要说明的是文中预测模型是根据民勤地区风沙土试验资料而建，众所周知，土壤特性普遍存在变异性，土壤质地结构对湿润体特性有较大影响，对于不同沙漠区的风沙土，文中所建预测模型系数还需修正。

作为近年来发展起来的节水控温技术，竖管地表滴灌尚处于初步探索阶段，本文仅研究了滴头流量、竖管直径、竖管埋深对竖管地表滴灌入渗特性的影响，后续仍需系统开展不同技术参数组合下竖管地表滴灌土壤水热迁移规律研究，以实现深根系植物节水控温理论的创新，为中国风沙防治和生态恢复提供一种可靠的思路和一种可靠的新方法。

5 结 论

通过12组竖管内积水入渗试验和9组竖管地表滴灌入渗试验，研究了不同影响因素下风沙土累积入渗量和湿润体运移变化过程，得到如下结论：

1）竖管直径一定时，稳渗率随埋深的增大而减下，竖管埋深一定时，稳渗率随管径的增大而增大；构建了稳渗率与竖管直径、竖管埋深之间的幂函数连乘模型（决定系数2>0.99），幂函数指数分别为2.01和-0.64，利用所建模型能够确定与竖管结构参数相匹配的滴头流量。

2）滴头流量对垂直向下湿润锋运移距离影响显著，滴头流量越大，垂直向下湿润锋运移距离越大，而水平方向和垂直向上湿润锋运移距离差异较小；在3个方向上湿润锋运移距离均随竖管直径的增大而减少；随竖管埋深增大，垂直向上和垂直向下湿润锋运移距离均有所减小，但水平方向湿润锋运移距离变化很小。

3）确定了灌溉水到达竖管底孔所需时间计算式，在此基础上，构建了包括滴头流量、竖管直径、竖管埋深和灌水时间在内的竖管地表滴灌湿润体预测模型，验证所建模型的可靠性，平均绝对误差和均方根误差平均值分别为0.74和0.92 cm，纳什效率系数均大于0.91，模型预测效果良好，可为竖管地表滴灌系统优化设计提供参考。

[1] 国家林业局. 中国第五次全国荒漠化和沙化状况公报[EB/OL].2015-12-29[2016-05-05].http://www.forestry.gov.cn/ main/69/ content-831684.html.

[2] 管梦鸾，张正偲，董治宝. 风沙灾害风险评估研究进展[J]. 中国沙漠，2018，38(5)：978-988.

Guan Mengluan, Zhang Zhengcai, Dong Zhibao. Progresses on the research of aeolian disaster risk assessment[J]. Journal of Desert Research, 2018, 38(5): 978-988. (in Chinese with English abstract)

[3] Li X R, Ma F Y, Xiao H L, et al. Long-term effects of revegetation on soil water content of sand dunes in arid region of Northern China[J]. Journal of Arid Environments, 2004, 57(1): 1-16.

[4] Ala M, Jiang D G, Niu C Y. The applicable density of sand-fixing shrub plantation in Horqin Sand Land of Northeastern China[J]. Ecological Engineering, 2014, 64: 250-254.

[5] Li X R, Zhang Z S, Huang L, et al. Review of the ecohydrological processes and feedback mechanisms controlling sand-binding vegetation systems in sandy desert regions of China[J]. Chinese Science Bulletin, 2013, 58(13): 1483-1496.

[6] 张增志，杜红梅，渠永平. 沙漠水科学材料研究综述[J]. 中国材料进展，2018，37(2)：81-87.

Zhang Zengzhi, Du Hongmei, Qu Yongping. Review on desert water science materials[J]. Materials China, 2018. 37(2): 81-87. (in Chinese with English abstract)

[7] Yu T, Ren C, Zhang J, et al. Effect of high desert surface layer temperature stress on haloxylon ammodendron (C.A. Mey.) Bunge[J]. Flora, 2012, 207(8): 572-580.

[8] Bita C E, Gerats T. Plant tolerance to high temperature in a changing environment: Scientific fundamentals and production of heat stress-tolerant crops[J]. Frontiers in Plant Science, 2013, 4: 1-17.

[9] 麻浩，张桦，马林，等. 无灌溉管件防护梭梭荒漠造林新技术及其示范推广[J]. 中国科学：生命科学，2014，44(3)：248-256.

Ma Hao, Zhang Hua, Ma Lin, et al. None-watering and tube-protecting planting technique for Haloxylon ammodendron under desert and its extension[J]. Scientia Sinica Vitae, 2014, 44(3): 248-256. (in Chinese with English abstract)

[10] 王泽，梁燕，阿不都克玉木·米吉提，等. 防护条件下梭梭幼苗生长及养分吸收特性[J]. 干旱区研究，2017，34(1)：112-118.

Wang Ze, Liang Yan, Abuttukeyom Mijit, et al. Growth and nutrient accumulation of Haloxylon ammodendron seedlings under protection conditions[J]. Arid Zone Research, 2017, 34(1): 112-118. (in Chinese with English abstract)

[11] 李久生，栗岩峰，王军，等. 微灌在中国：历史、现状和未来[J]. 水利学报，2016，47(3)：372-381.

Li Jiusheng, Li Yanfeng, Wang Jun, et al. Microirrigation in China: history, current situation and prospects[J]. Journal of Hydraulic Engineering, 2016, 47(3): 372-381. (in Chinese with English abstract)

[12] 田富强，温洁，胡宏昌，等. 滴灌条件下干旱区农田水盐运移及调控研究进展与展望[J]. 水利学报，2018，49(1)：126-135.

Tian Fuqiang, Wen Jie, Hu Hongchang, et al. Review on water and salt transport and regulation in drip irrigated fields in arid regions[J]. Journal of Hydraulic Engineering, 2018, 49(1): 126-135. (in Chinese with English abstract)

[13] 白丹，何靖，郭霖，等. 地下灌竖管灌水器直径压力对土壤水入渗特性的影响[J]. 农业工程学报，2016，32(14)：97-102.

Bai Dan, He Jing, Guo Lin, et al. Effects of pressure head and vertical tube diameter on infiltration characteristics of soil moisture in subsurface irrigation system with vertical tube emitter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(14): 97-102. (in Chinese with English abstract)

[14] 吕谋超，仵峰，彭贵芳. 地下和地表滴灌土壤水分运动的室内试验研究[J]. 灌溉排水学报，1996，15(1)：42-44.

Lǚ Mouchao, Wu Feng, Peng Guifang, et al. Experimental study on soil water movement of subsurface and surface drip irrigation[J]. Journal of Irrigation and Drainage, 1996, 15(1): 42-44. (in Chinese with English abstract)

[15] Kandelous M M, Šimůnek J. Comparison of numerical, analytical, and empirical models to estimate wetting patterns for surface and subsurface drip irrigation[J]. Irrigation Science, 2010, 28(5): 435-444.

[16] Monjezi M S, Ebrahimian H, Liaghat A, et al. Soil wetting front in surface and subsurface drip irrigation for silty loam soil[J]. Proceedings of the Institution of Civil Engineers-Water Management, 2013, 166(5): 272-284.

[17] 孙西欢，马娟娟，周青云，等. 蓄水坑灌法技术要素初探[J]. 沈阳农业大学学报，2004，35(5)：405-407.

Sun Xihuan, Ma Juanjuan, Zhou Qingyun, et al. A preliminary research on the technical elements of water storage pit irrigation method[J]. Journal of Shenyang Agricultural University, 2004, 35(5): 405-407. (in Chinese with English abstract)

[18] 吴普特，汪有科，辛小桂，等. 陕北山地红枣集雨微灌技术集成与示范[J]. 干旱地区农业研究，2008，26(4)：1-6.

Wu Pute, Wang Youke, Xin Xiaogui, et al. Integration and demonstration of the date micro-irrigation technology in the hilly of Shanbei[J]. Gricultural Research in the Arid Areas, 2008, 26(4): 1-6. (in Chinese with English abstract)

[19] 赵伟霞，张振华，蔡焕杰，等. 间接地下滴灌导水装置规格参数模型[J]. 水利学报，2009，40(3)：355-363.

Zhao Weixia, Zhang Zhenhua, Cai Huanjie, et al. Parameter model of water-conducting device specification for indirect subsurface drip irrigation[J]. Journal of Hydraulic Engineering, 2009, 40(3): 355-363. (in Chinese with English abstract)

[20] 曾辰，王全九，樊军. 初始含水率对土壤垂直线源入渗特征的影响[J]. 农业工程学报，2010，26(1)：24-30.

Zeng Chen, Wang Quanjiu, Fan Jun. Effect of initial water content on vertical line-source infiltration characteristics of soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(1): 24-30. (in Chinese with English abstract)

[21] 张建丰，李涛，张江辉，等. 极端干旱区成龄葡萄深层坑渗灌技术研究[J]. 灌溉排水学报，2011，30(1)：69-71.

Zhang Jianfeng, Li Tao, Zhang Jianghui, et al. Technique factors of the deep pit infiltration irrigation for mature grapes in extremely arid area[J]. Journal of Irrigation and Drainage, 2011, 30(1): 69-71. (in Chinese with English abstract)

[22] 余小弟，刘小刚，朱益飞，等. 土壤质地和供水压力对竖插式微润管入渗的影响[J]. 排灌机械工程学报，2017，35(1)：71-79.

Yu Xiaodi, Liu Xiaogang, Zhu Yifei, et al. Effects of soil texture and water pressure on moistube infiltration in vertical inserting mode[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(1): 71-79. (in Chinese with English abstract)

[23] Philip J R. The theory of infiltration: 4. sorptivity and algebraic infiltration equations[J]. Soil Science, 1957, 84(3): 257-264.

[24] 范严伟，赵彤，白贵林，等. 水平微润灌湿润体HYDRUS-2D模拟及其影响因素分析[J]. 农业工程学报，2018，34(4)：115-124.

Fan Yanwei, Zhao Tong, Bai Guilin, et al. HYDRUS-2D simulation of soil wetting pattern with horizontal moistube-irrigation and analysis of its influencing factors[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018,34(4):115-124.(in Chinese with English abstract)

[25] 陆军胜，张富仓，范军亮，等. 不同滴头流量和灌水量下农田土壤湿润体特征及其估算模型[J]. 干旱地区农业研究，2020，38(4)：19-26.

Lu Junsheng, Zhang Fucang, Fan Junliang, et al. Characteristics and estimation model of wetted soil volume under different drip discharge rates and irrigation amounts[J]. Agricultural Research in the Arid Areas, 2020, 38(4): 19-26. (in Chinese with English abstract)

[26] Fan Y W, Shao X X, Gong J G, et al. An empirical model for estimating soil wetting pattern dimensions during film hole irrigation[J]. Archives of Agronomy and Soil Science, 2020, 66(13): 1765-1779.

[27] 唐士劼，窦超银. 滴头流量对风沙土滴灌风沙土湿润锋运移影响的试验研究[J]. 节水灌溉，2018(11)：56-60，72.

Tang Shijie, Dou Chaoyin. An experiment study of the effects of dripper discharge on soil wetting front under drip irrigation in aeolian sandy soil[J].Water Saving Irrigation, 2018(11): 56-60,72. (in Chinese with English abstract)

[28] 陈渠昌，吴忠渤，佘国英，等. 滴灌条件下沙地土壤水分分布与运移规律[J]. 灌溉排水学报，1999，18(1)：3-5.

Chen Quchang, WuZhongbo, She Guoying, et al. Water distribution and transport in sandy soil under drip irrigation[J]. Irrigation and Drainage, 1999,18(1): 3-5. (in Chinese with English abstract)

[29] 胡笑涛，康绍忠，马孝义，等. 地下滴灌条件下沙质土壤入渗特性试验研究[J]. 灌溉排水学报，2004，23(5)：75-77.

He Xiaotao, Kang Shaozhong, Ma Xiaoyi, et al. Experiment on sandy soil infiltration under subsurface drip irrigation[J]. Journal of Irrigation and Drainage, 2004, 23(5): 75-77. (in Chinese with English abstract)

[30] 白丹，孙淑贞，任培琦，等. 地下灌竖管灌水器湿润体时空变化规律[J]. 农业工程学报，2018，34(7)：107-113.

Bai Dan, Sun Shuzhen, Ren Peiqi, et al. Temporal and spatial variation of wetting volume under sub-irrigation with vertical emitter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 107-113. (in Chinese with English abstract)

[31] 范严伟，白贵林，赵文举，等. 重力式地下孔灌土壤水分运动规律试验研究[J]. 兰州理工大学学报，2020，46(1)：65-70.

Fan Yanwei, Bai Guilin, Zhao Wenju, et al. Experimental investigation of movement regularity of soil moisture during gravity-type underground hole irrigation[J]. Journal of Lanzhou University of Technology, 2020, 46(1): 65-70. (in Chinese with English abstract)

Estimation model for steady infiltration rate and wetting pattern of aeolian sandy soil under vertical pipe surface drip irrigation

Fan Yanwei, Wang Yanxiang, Zhu Pengcheng, Yang Zhiwei

(730050)

Vertical-pipe drip irrigation is one of the most efficient state-of-the-art techniques for water-saving and temperature conservation, thereby alleviating the combined stress of drought and high temperature in sand-fixing plant seedlings. In terms of long-term engineering, it is necessary to explore the infiltration characteristics of aeolian sandy soil under vertical-pipe drip irrigation. Furthermore, the discharge rate of the drip system is required less than the stable infiltration rate of water in a critical depth, in order to meet the requirement of no flooding seedlings when the emitter is combined with the vertical pipe. In this study, a ponding infiltration test was carried out using a 2 cm constant head in the field to investigate the variation process of cumulative infiltration of aeolian sandy soil under different buried depths and diameters of vertical pipe. A Philip infiltration model was established to fit the data. 9 treatments and 3 control tests were included in the infiltration experiment. Specifically, the diameter of the vertical pipe was designed with the levels of 8.8, 10.6, 12.6, and 14.2 cm, while the buried depth was set at 15, 20, and 25 cm. The results show that the stable infiltration rate of Philip model increased as the diameter of vertical pipe increased, and decreased with the increase of buried depth. A power function relationship (2> 0.99) was followed between the steady permeability rate and the diameter or buried depth of vertical pipe, where the power function indexes were 2.01 and -0.64, respectively. The well-established estimation formula of stable infiltration rate was also utilized to determine the drip discharge matching with the structural parameters of the vertical pipe, when there was no ponding in the vertical pipe. Subsequently, the infiltration test was conducted for the vertical-pipe drip irrigation. A field test was also carried out to observe the movement of wetting front in aeolian sandy soil under the different dripper discharge, buried depth, and diameter of vertical pipe. A power function was used to process the observed data. 7 treatments and 2 control tests were included in the field test. The dripper discharge was designed with the different levels of 0.9, 1.2, and 1.5 L/h, where the diameters of the vertical pipe were 10.6, 12.6, and 14.2 cm, and the buried depths of the vertical pipe were 15, 20, and 25 cm. The results showed that there was a significant effect of dripper discharge on the migration distance of the wetting front in the vertical downward. The migration distance of the wetting front was much greater in the vertical downward, whereas, slightly increased in the horizontal and vertical upward, as the dripper discharge became larger. Additionally, the migration distance of the wetting front in three directions decreased with the increase in the diameter of the vertical pipe. The migration distance of the wetting front in vertical upward and downward decreased, but the horizontal migration distance changed little, as the depth of the vertical pipe increased. The time of irrigation water was determined to reach the bottom hole of the vertical pipe, according to the water balance equation. A prediction model of the wetting body was established for the vertical-pipe drip irrigation, including the emitter discharge, diameter, and buried depth of the vertical pipe, as well as the irrigation time. The model was also verified by the 8 and the 9 schemes of the irrigation test. The average absolute error of the model was between 0.28 cm and 1.07 cm, while the root mean square error was between 0.19 cm and 1.68 cm, and the Nash efficiency coefficient was greater than 0.91. The finding can offer the accurate prediction of steady infiltration rate and wetting body in the optimal design of vertical-pipe drip irrigation system, thereby creating a relatively suitable environment for sand-fixing plant seedlings.

irrigation; infiltration;models; wetting pattern; steady infiltration rate; vertical pipe surface drip irrigation

2020-12-09

2021-03-01

国家自然科学基金项目（51969013）；甘肃省自然科学基金项目（18JR3RA144）

范严伟，博士，副教授，研究方向为水土资源利用和节水灌溉技术。Email：fanyanwei24@163.com

10.11975/j.issn.1002-6819.2021.07.013

S275.6

A

1002-6819(2021)-07-0103-09

范严伟，王延祥，朱鹏程，等. 竖管地表滴灌下风沙土稳定入渗率与湿润体估算模型[J]. 农业工程学报，2021，37(7)：103-111. doi：10.11975/j.issn.1002-6819.2021.07.013 http://www.tcsae.org

Fan Yanwei, Wang Yanxiang, Zhu Pengcheng, et al. Estimation model for steady infiltration rate and wetting pattern of aeolian sandy soil under vertical pipe surface drip irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(7): 103-111. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.07.013 http://www.tcsae.org