地铁公交线路合作博弈研究

周雨阳，刘国鹏，陈艳艳,b，闫慧雅

(北京工业大学，a.交通工程北京市重点实验室；b.交通运输部城市公共交通智能化行业重点实验室，北京100124)

0 引言

作为城市公共交通中最主要的两种交通服务方式，地铁和公交线路间的合作博弈关系是在客流资源有限的前提下，为实现降低成本、提高服务质量、增加公共交通整体占有率，共同挖掘潜在收益，构建的一种地铁公交一体化新趋势。YAO B.Z.[1]等通过两个公交线路的一体化合作运营，说明合作可以降低线路的运营成本。而以往研究大多认为两者之间的关系是非合作关系。马超群[2]等通过Logit模型构建了轨道交通和常规公交间的竞争模型，确定两者的客流量分担率。但随着交通线网的逐步饱和，地铁和公交线路的独立运营已经无法满足交通需求。公交线路成本低、布线灵活、覆盖高的特征可以弥补地铁线路固定站点、高投入的不足，进行优势互补，达成合作博弈关系，构建地铁公交一体化的新型交通网络。此外，一体化的公共交通网络，既便于政府调节公共交通系统内的客流走向，又能保障各方利益。

针对交通运输系统内的合作博弈关系，有很多研究案例。赵峰等[3]通过广义费用模型对轨道交通内多个运营商之间的收益进行分配。Jiang C.等[4]通过构建数学模型分析得出，高铁和民航的合作关系在不同的合作场景下受到其服务质量的影响。焦薇等[5]针对物流园区的合作共生系统，提出了基于Nash协商模型和夏普利值法的合作收益分配模型。Algaba E.[6]等在一卡通行的前提下分析了多种交通方式运营商之间合作博弈问题，并提出了两种收益方案。可以发现，参与合作博弈的个体，其根本动力是获得额外收益。在地铁和公交线路间的合作运输联盟中，公平合理地分配收益则能维系合作博弈关系，为后续的地铁公交一体化趋势稳定、高效运作奠定基础。对此，本文提出一种适用于地铁线路和公交线路双方的合作博弈模型，根据线路间的结构关系将地铁和公交的运营合作分为联合运输和共同运输两种模式，分别构建了基于路网贡献度的分配法和基于多因素影响的夏普利修正值分配法，并给出收益分配方案的算例分析。

1 合作博弈模型

1.1 问题假设

给定一个有向交通网络N=(V,U,L)，其中，V为网络中节点v的集合，V=(1,2,…,v)；U为网络上线路运营商u的集合，U=(1,2,…,u)；L⊂V×V×U为网络中任意两个节点间由各运营商承担运输的线路l集合，L=(1,2,…,l)。R为网络中出行路径r的集合，R=(1,2,…,r)，每个路径r由若干相邻的可换乘线路l连接组成，即当两点i,j之间可通行线路或路径不唯一时，乘客在完全理性的基础上，根据自身需求和外部因素选择出行线路，路径的被选择概率为q(l)。Ru为出行路径中运营商u参与完成的路径集合，Ur为出行路径r上运营商的集合，cu为交通网络中运营商u在路径上的单位运营成本，p(i,j)为节点i,j间的客流总量，t(u)为运营商u在节点i,j间运营线路l上的票价，b为运营商u在线路l上运营线路的补贴收益。综上，运营商u在运营线路l上的收益函数为

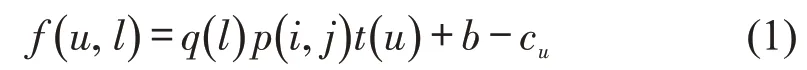
运营商u在出行路径r上的收益函数为

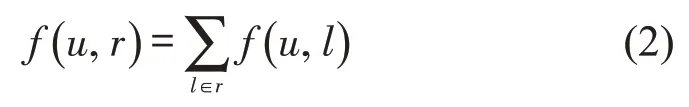
运营商u在交通网络N上的总收益函数为

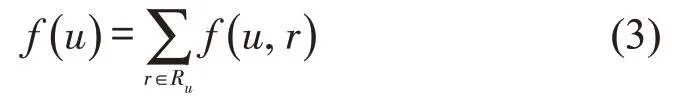
合作运输的前提是运营参与者可以通过合作获得更多的收益，本文以地铁和公交的运营商集合U作为合作联盟的参与者，构建合作博弈模型(U,f)，f为各运营商的收益函数，满足

式中：|U|为联盟中的参与者数量。假设合作联盟集合中存在两个联盟S和M，S⊂M⊆U{i}，满足

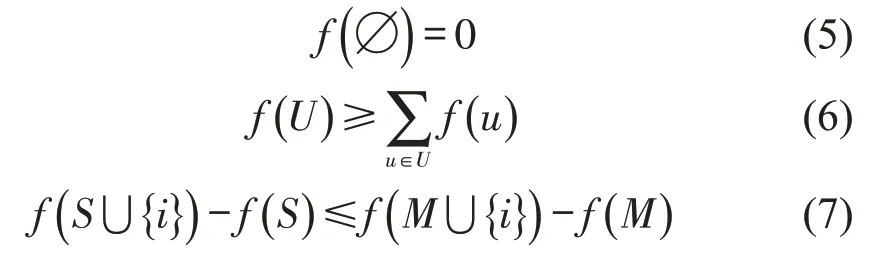
说明地铁和公交的合作联盟具有凸性，即联盟越大，合作收益越高。运营商可以通过加入合作联盟，创造新的合作剩余价值。该合作运输联盟可以成立，但联盟能否稳定维持，取决于如何分配合作剩余价值，使得每个运营商的收入与其合作中的贡献相匹配。

1.2 考虑各项成本的收益分配模型

在地铁和公交构成的公共交通网络中，根据运营线路在交通拓扑网络的关系是衔接关系还是平行关系，将其合作运输分为联合运输模式和共同运输模式。

(1)联合运输模式(Intermodal Transportation，IT)，即客流在出行路径r上经由不同线路连接完成出行。如图1所示，箭头表明出行路径r=(l1,l2)的方向，客流从节点1 出发，途径节点2，去往节点3，此路径上的客流运输需要联合使用运营商u1的线路l1=(1,2,u1)和运营商u2的线路l2=(2,3,u2)来合作完成。

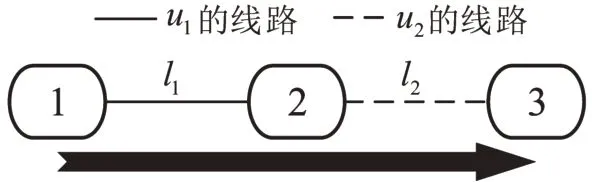
图1 联合运输模式Fig.1 Intermodal transportation

在IT 模式中，客流通过换乘不同线路前往目的地，出行链上游线路对下游线路获得的客流收益付出了贡献，理应获得部分收益分成。因此，IT 模式的收益分配分成3 种场景：①线路l=l1，即线路处于出行链上游，客流从当前线路出发换乘到下一线路到达目的地，当前线路可以从后续线路中获得额外收益；②线路l=l2，即线路处于出行链下游，客流从上一线路出发换乘到当前线路到达目的地，当前线路需要让出部分收益给上游线路；③线路l=l3，即线路处于出行链中游，客流从上游线路经过当前线路前往下一线路，该情景不仅包含了情景1 中的获得，还包含了情景2 中的让出。收益分配表达式为

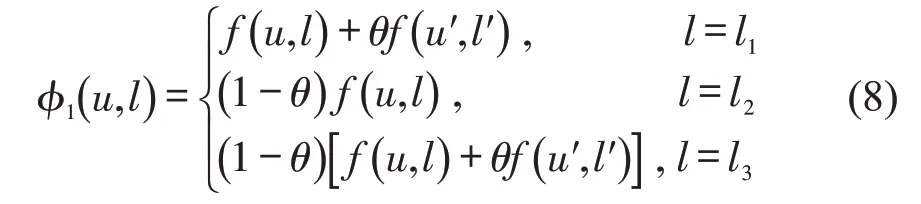
式中：θ为联合运输模式中线路在出行中的分配参数；l′为处于线路l下游由另一家运营商u′运营的线路，两条线路共同组成了出行路径。

(2)共同运输模式(Shared Transportation，ST)，即在出行路径r上有多条线路可同时供乘客出行选择。如图2所示，箭头表明出行路径的走向，客流从节点1 去往节点2，可以根据个人需求和外部影响因素选择使用运营商u1的线路l1=(1,2,u1) 或是运营商u2的线路l2=(1,2,u2) 来完成出行。

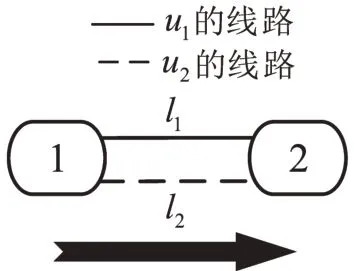
图2 共同运输模式Fig.2 Shared transportation

此时不同线路组成的合作运输联盟共同承担了网络节点间的客流运输任务。对于其合作收益，本文构建了基于夏普利修正值的收益分配模型，引入修正因子调整对合作收益的分配，避免原夏普利值模型中的平均分配现象。收益分配表达式为

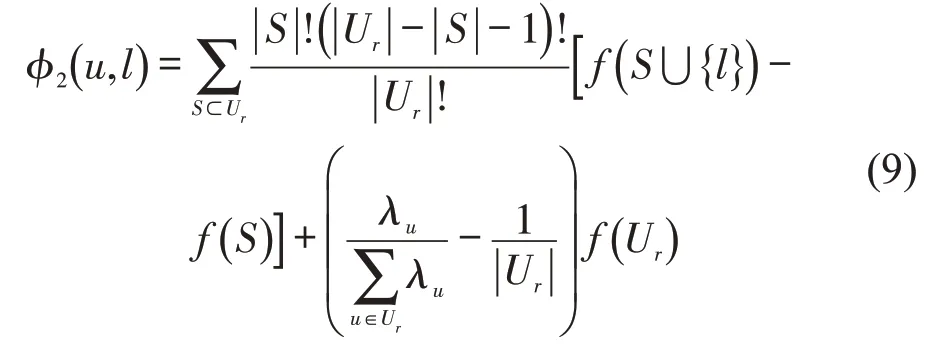
式中：λu为修正因子；为合作参与者u的综合评价值与联盟平均值的差值。修正因子λu的计算公式为

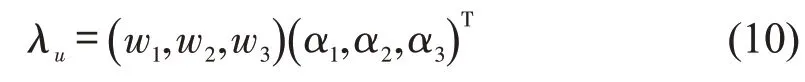
式中：wi为第i个影响因素的权重，且为第i个影响因素的综合评价值，研究选取的影响因素如下。

①贡献系数α1

在共同运输模式里，各运营商为服务交通出行所做出的贡献，及承载客流的多少。需注意，共同运输模式的贡献系数与联合运输模式的贡献系数是不同的系数指标，两者取值可以相同，但意义不同。

②运营成本系数α2

从运营商在线路投入成本的角度，衡量运营商对路径上乘客出行的贡献参与度。

③合作风险系数α3

在共同模式中，不同的运营商需要承担不同的合作风险，作为出行服务的供给方始终有竞争的存在。

经过分配后的各运营商在交通网络上的总收益f′(u)为联合运输收益加上无需分配的收益和共同运输的收益，即

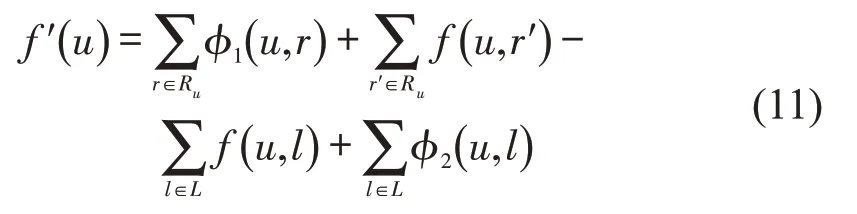
式中：r′为运营商u独自完成的出行路径，且Ru={r,r′}。

2 数值算例分析

2.1 案例参数

不失一般性，给定一个交通网络N=(4,3,5)，如图3所示。图中3个运营商承担的运营线路分别用3种线型表示：实线是地铁运营商u1，运营2条线路分别是(1,2)和(2,4)；虚线是公交运营商u2，运营(1,2)、(2,3)和(3,4)这3 条线路；点虚线是公交运营商u3，运营了(1,3)和(3,4)这2条线路。

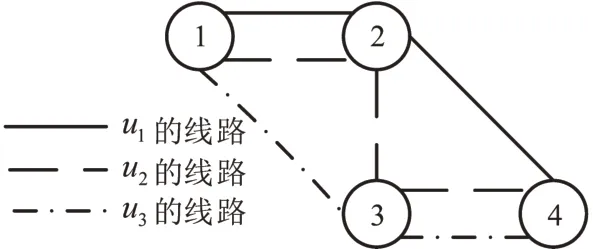
图3 交通网络Fig.3 A traffic network

地铁单位票价t1=3 元，公交单位票价t2=t3=1元。地铁线路成本c1=500 元，公交线路成本分别为c2=700 元和c3=600 元。设联合运输模式的分配参数为θ=0.2，共同运输模式中各运营商的修正参数为权重(w1,w2,w3)=(0.3,0.3,0.4)，可算得λu1=0.4，λu2=0.3，λu3=0.3。每条路径上的政府补贴为b=1000 元。

一般交通网络中客流是双向流动，为简便计算过程且不失一般性，只计算一个方向，即从编号较小站点到编号较大站点的客流方向，可以得到系统中共存在19条路径。节点的多个路径被选择的概率n为节点间可选路径数，节点间的客流被可行路径平分，因此假设每个路径上的客流均是1000人，得到系统总流入客流为19000人。网络上系统外换乘代价为无穷大，即当路径上不同运营商的线路不合作时，出行无法完成，认为该路径上的客流因得不到服务而离开了公共交通系统。算例网络中的可行线路及收益如表1所示。

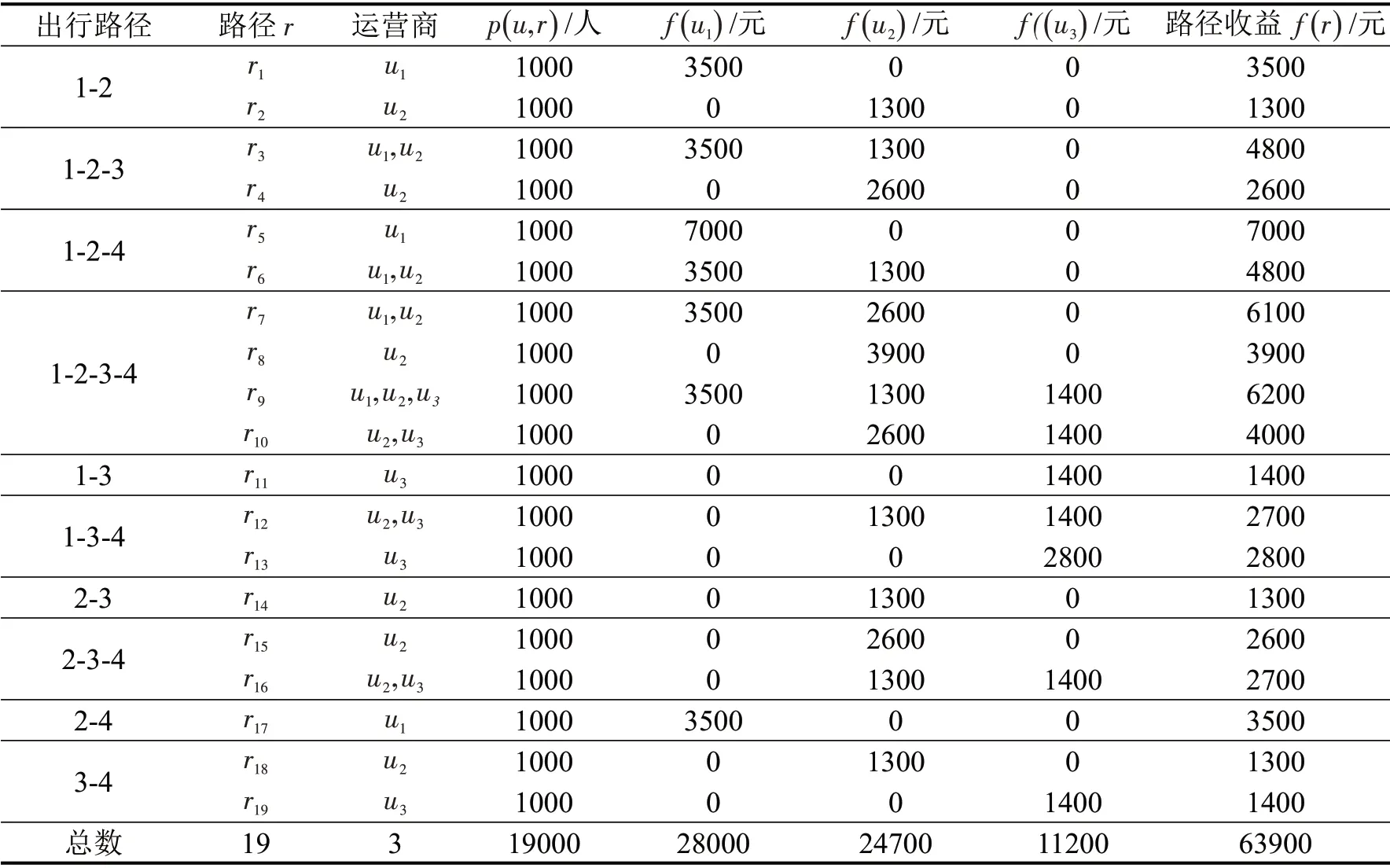
表1 交通网络中各线路上的收益Table 1 Profit of each routs in a simple traffic network

合作博弈中，各运营商有3 种可选策略：独自运营、两两合作和全部合作，各种策略下的收益情况如表2所示。可以发现，地铁和公交运营商之间的合作可以扩大联盟收益，此合作博弈是凸博弈，存在联盟越大，合作收益越大的特点，合作可以持续，而且博弈核心不为空，夏普利值处于核心内[6]。

表2 合作博弈中各策略下的收益Table 2 Profit of each strategy in cooperative game

2.2 利润分配

交通网络中联合运输模式和共同运输模式是同时存在的，在制定各运营商的收益分配顺序时，考虑到共同运输模式中并行线路是作为一个整体参与出行链，故先进行联合运输模式的收益分配，再进行共同运输模式的收益分配，具体分配过程如下。

Step 1 计算未分配时各运营商收益情况，并将收益分配到网络中的线路上，如表3所示。

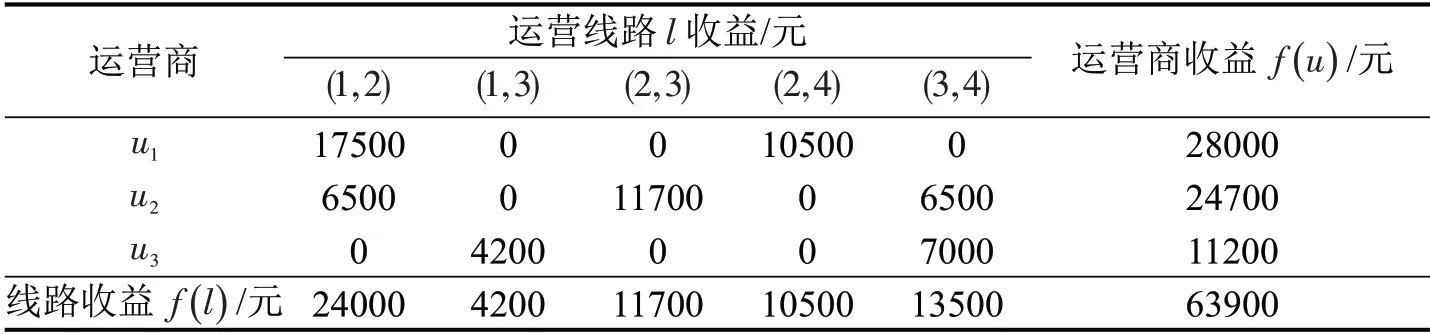
表3 各运营商未进行重分配的收益Table 3 Profit of operator without redistribute

Step 2 计算联合运输模式下线路的收益分配

通过路径上参与运营的运营商个数，可以判断采用联合运输模式的出行路径有7条，分别为路径3、6、7、9、10、12和16。基于本文第1节提出的联合运输模式下线路收益分配方法，对其收益进行分配，结果如表4所示。

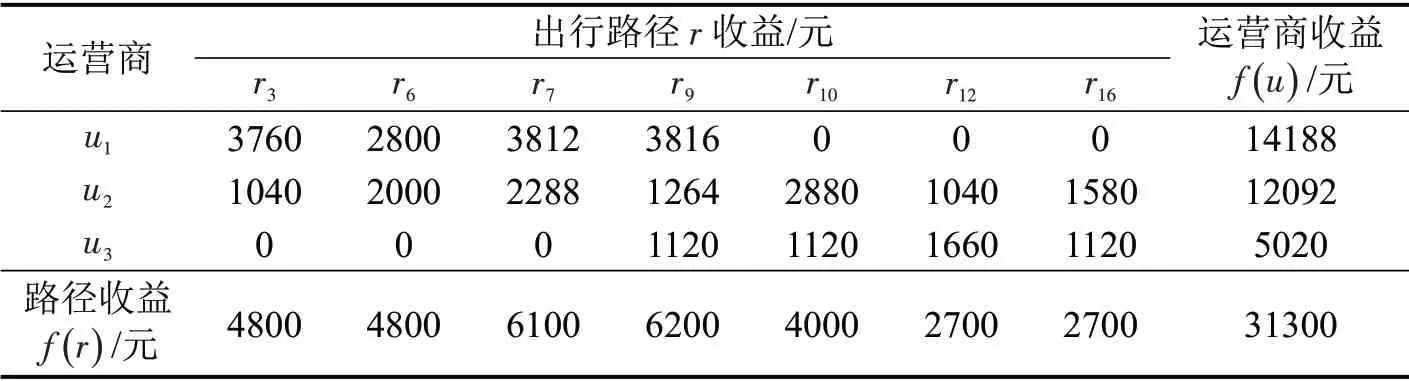
表4 联合运输模式路径收益分配Table 4 Profit distribution of routs of intermodal transportation

将该收益分配结果，重新整合到交通网络线路上，得到联合运输模式收益分配后各运营商的收益情况，如表5所示。

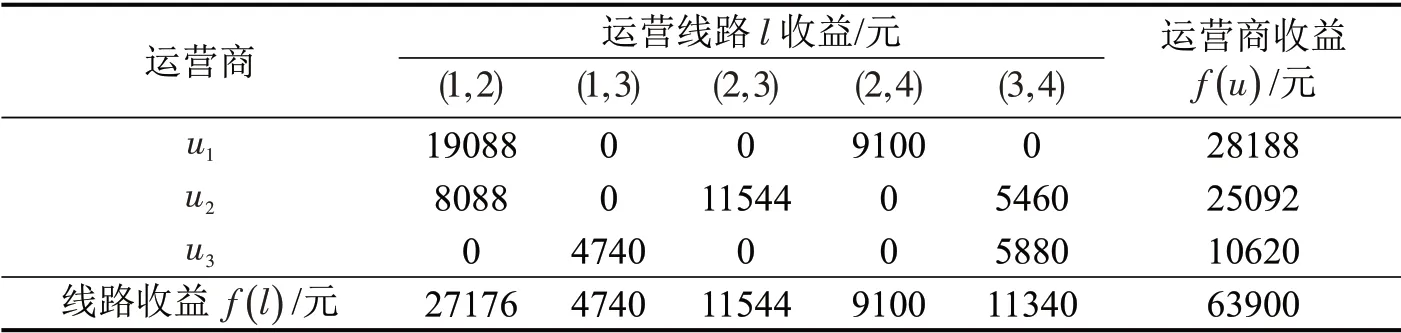
表5 联合运输部分各运营商收益分配Table 5 Profit distribution of operator under intermodal transportation

Step 3 计算共同运输模式下线路的收益分配

采用共同运输模式的线路是(1,2)和(3,4)，分别由运营商u1,u2和u2,u3进行合作运输。以线路(1,2) 为例，运营商u1,u2独立运营的收益分别为7700 元和4472 元，合作运输产生的额外收益为15004 元。表6为运营商u1在线路(1,2)上的夏普利修正值计算过程，可知运营商u1的总收益为16273 元。同理可得运营商u2在线路(1,2)和(3,4)的收益分别为10903 元和6620 元，运营商u3在线路(3,4)的收益为4720元。

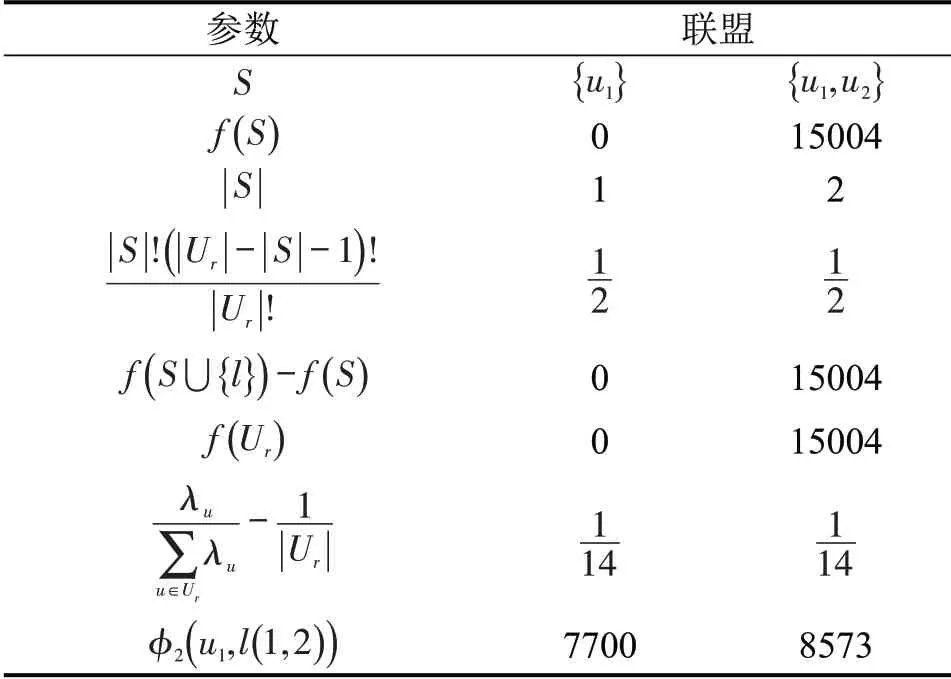
表6 运营商u1 在线路(1,2)上的夏普利修正值计算过程Table 6 Shapley correction value calculation for u1 on line(1,2)

至此，合作运输联盟中各运营商的收益分配完毕，收益情况如表7所示。

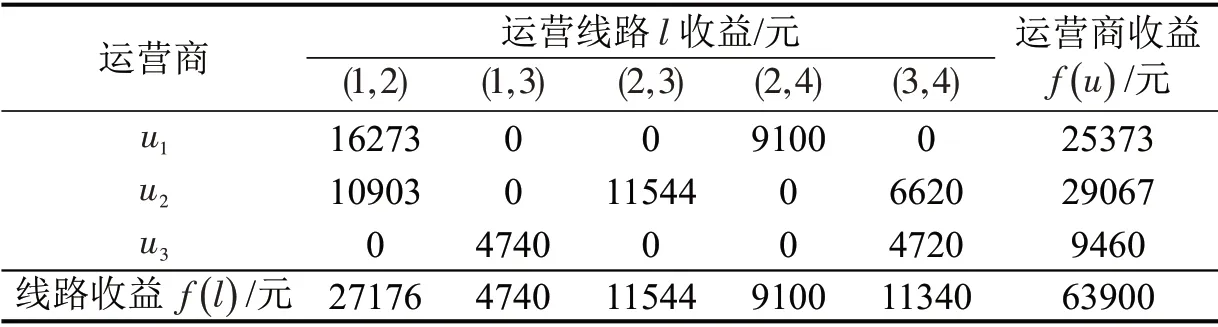
表7 共同运输分配后运营商的收益情况Table 7 Profit of operator under shared transportation

2.3 结果分析

合作运输联盟的成立首先要满足收益增加，其次是合作收益的分配合理性，维护各方参与者的利益。从表8可以看出，合作运输后总利润为63900元，增长了96%，对其进行完全分配后，各运营商的收益都比独立运营时有较大幅度的增长，这与合作运输联盟的初衷一致。值得注意的是，运营商u2的增长幅度最大，达到了123.60%。这是因为u2运营的3条线路参与完成了13条出行路径，占总路径数的68.42%，是交通网络中贡献最大的运营商。

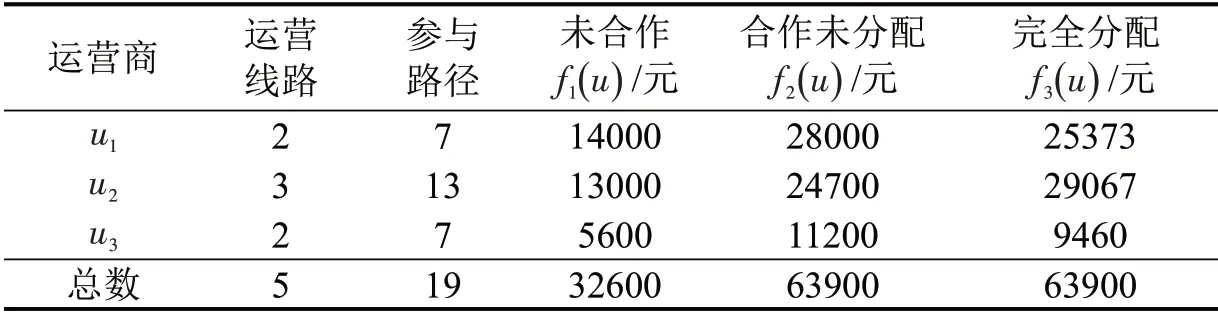
表8 各运营商合作运输前后的收益对比Table 8 Profit of operator before and after cooperative transportation

联合运输模式中，下游线路向上游线路让渡部分收益来维系合作运输联盟，因此合作后运营商u1和u3运营的线路数和参与完成的路径数一致，但当前方向上u3的收益仅增长了68.90%，低于u1的81.24%。但交通出行是双方向的，当前方向的下游线路在相反的出行方向就会成为上游线路，同样收益增长情况也会出现对调，实现收益分配的平衡。

共同运输模式中，修正因子的大小受影响因子(α1,α2,α3)和因子权重(w1,w2,w3)的共同影响。影响因子(α1,α2,α3)应由合作运输联盟共同制定取值规则。利用w1+w2+w3=1 可以画出各项权重对修正因子的影响情况，图4为运营成本和贡献系数两者的权重与修正因子间的关系。图中，灰色平面代表u1的修正因子λ1，黑色平面代表u2和u3的修正因子λ2=λ3；白实线是三者修正因子全等时的条件，即权重关系满足；白虚线左侧是u1更占优势，可以分得更多收益，右侧则是u2或u3获益更多。因此权重的确定，需要政府作为第三方根据交通运营中的实际状况进行确定。

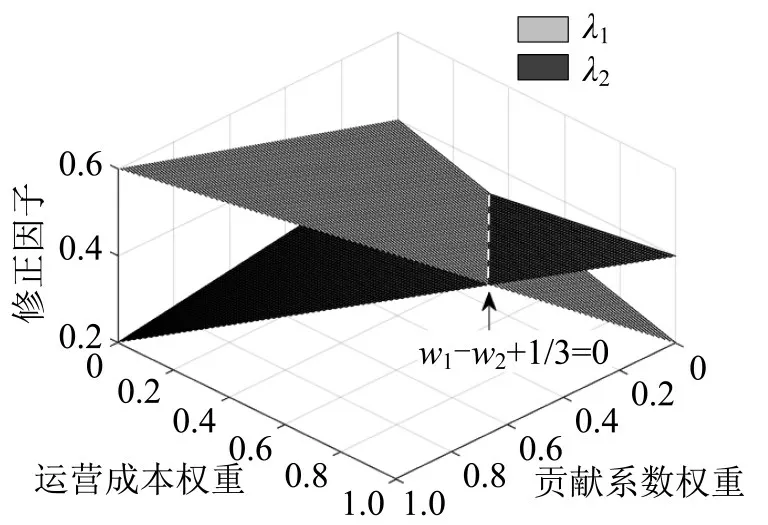
图4 修正因子与运营成本权重和贡献系数权重的关系Fig.4 Relationship between correction factor and weight of operating cost and contribution coefficient

3 结论

地铁和公交线路通过合作博弈构建一体化的交通网络，将过去的客流竞争关系转变为收益共享关系。维系合作联盟需要公平合理地分配合作产生的收益。本文基于合作博弈理论，将线路间的结构关系引入到收益分配模型的构建中。通过算例结果可知，该模型既保证了交通网络中高贡献度的运营商获得更多收益，也将交通双方向间的收益分配进行了平衡，同时可通过调整权重变化影响收益分配结果，具有合理性、公平性和可调节性。