基于深度学习的车辆轨迹重建与异常轨迹识别

黄士琛，邵春福，李娟，张小雨，钱剑培

(北京交通大学，综合交通运输大数据应用技术交通运输行业重点实验室，北京100044)

0 引言

随着空间定位采样技术的发展和移动终端的普及，海量轨迹数据的知识发现成为交通领域的研究热点和趋势。车辆轨迹数据由于更新快、频率高，可以得到居民出行和交通运行状态等重要信息，成为数字交通的建设基石。车辆轨迹理应依附于城市道路网络，然而受到记录故障、定位故障和人工失误操作的影响，轨迹数据呈现出不确定性、稀疏性和偏态分布性等缺点[1]，无法精确依照出行者的出行行为和道路网络进行存储，进而产生异常点段，使其在交通领域的应用受到阻碍。因此，车辆轨迹重建与异常识别研究具有重要意义。

针对GPS轨迹异常识别，CHAWLA[2]根据交通小区的OD 矩阵，分析潜在的异常链路，再依据历史信息识别异常点段。吴玥琳[3]清洗并分析出租车的轨迹特点，从包围面积和相似度角度阐述轨迹特征并用于合乘行为研究。LEI[4]提出MT-MAD 框架，将轨迹按区域分割，根据区域内的轨迹特征分数排序，将分数超过阈值的轨迹视为异常。在轨迹重建方面，SPAGNOL[5]结合GPS 与另一组传感器的数据共同推算和重建移动轨迹。ZHANG[6]使用样条曲线函数拟合船舶的航向轨迹并表明性能优于多项式回归等模型。

本文尝试将对抗生成网络等深度学习方法应用于轨迹重建和异常识别。GOODFELLOW[7]提出基于对抗网络的生成模型(Generative Adversarial Networks，GANs)，模型里生成器和判别器两个神经网络经过反复博弈，使生成器逼近样本实际分布。HINTON[8]通过深度自编码网络(Autoencoder，AE)提取高维数据特征并表明AE是有效的参数预训练方法。段宗涛[9]使用长、短时记忆神经网络(Long Short-term Memory，LSTM)预测出租车需求并取得高准确率。YANG[10]提出能区别地关注重要和不重要特征的注意力模型(Attention)，用于文档分类并取得较高精度。

本文构建基于LSTM-AE-Attention 模型的轨迹重建与异常识别方法，针对车辆轨迹数据集中正常与异常数据不平衡问题，采用数据增强的思路，通过GANs和贝塞尔曲线丰富数据集的数量和种类。同时，针对深度学习参数不易标定的缺点，建立融合LSTM的AE模型自动提取轨迹中最具代表性的特征，在参数预训练的同时完成轨迹重建并使其更平滑。在异常识别中，引入注意力机制提升模型的分类精度。

1 问题描述

车辆k的出行轨迹为{Tk=(xi,yi)|i=1,2,…,r;k=1,2,…,m}，其中：xi、yi分别为车辆的经度、纬度(按时间升序排列)，m为全部车辆产生的轨迹总数，r为轨迹Tk中经纬度点的个数。若车辆k的轨迹Tk出现轨迹接收不全和轨迹定位漂移等误差，则定义Tk为异常轨迹并将lk赋值为1；否则，lk为0。每个Tk对应1 个是否为异常轨迹的标签lk，即{lk|lk∈{0,1},k=1,…,m}。轨迹示意如图1所示。

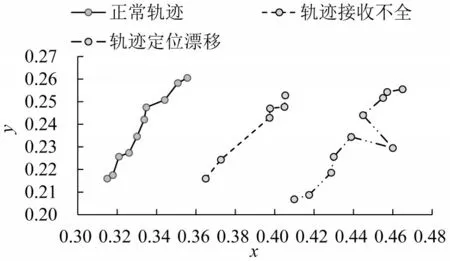
图1 正常轨迹和异常轨迹示意Fig.1 Normal and abnormal trajectory

由图1可知，正常轨迹和异常轨迹的区别较为明显，正常轨迹的线条相对光滑，轨迹点之间距离和角度的变化也较平缓；当轨迹接收出现间断时，部分轨迹点间将产生长距离间隔；当轨迹点定位发生漂移时，坐标点将产生剧烈的角度和位置变化。

本文需要从海量轨迹数据中提取特征，而手工提取特征(例如：统计轨迹的欧氏距离、速度等)不易囊括数据所蕴含的全部信息，故采用典型的自动提取特征的AE模型，通过模型中的编码器Q1和解码器Q2自动提取轨迹特征。轨迹重建是要找到神经网络Q1和Q2并使Q2[Q1(Tk)]=Tk构成恒等映射，用AE 来训练函数Q1和为重建后的轨迹。异常识别被归纳为1 个有监督的多分类问题，样本集为{(Tk,lk)|k=1,2,…,m}，输入为AE提取的特征Q1(Tk)，输出为lk。

2 模型构建

2.1 基于数据增强的样本集平衡方法

在分类问题中，样本集的正类与反类比例大于4∶1 时被认为不平衡。本文样本集{(Tk,lk)|k=1,2,…,m}，标签lk数量差别较大(正常与异常比例为12∶1)，故车辆轨迹数据集不平衡，修正方法包括：欠采样和过采样。

欠采样是随机去除多数类中的样本，使多数类和少数类的数量接近，但会丢失多数类的部分特征。过采样是将少数类扩增到与多数类相近的数量。本文将少数类(即异常轨迹数据)作为输入，使用基于GANs的过采样方法，通过训练不断逼近少数类分布，产生人工合成的异常轨迹，从而均衡不平衡样本集。此外，Tk也可以代表动物、台风等物体的移动规律，因此，模型不仅需要识别正常和异常的交通轨迹，还应具备识别交通和非交通轨迹的能力。如图2所示，本文一方面通过人工合成异常轨迹改善样本数量不平衡的问题，另一方面增加非交通轨迹，扩展数据多样性，从样本数量和类别两方面实现数据增强。

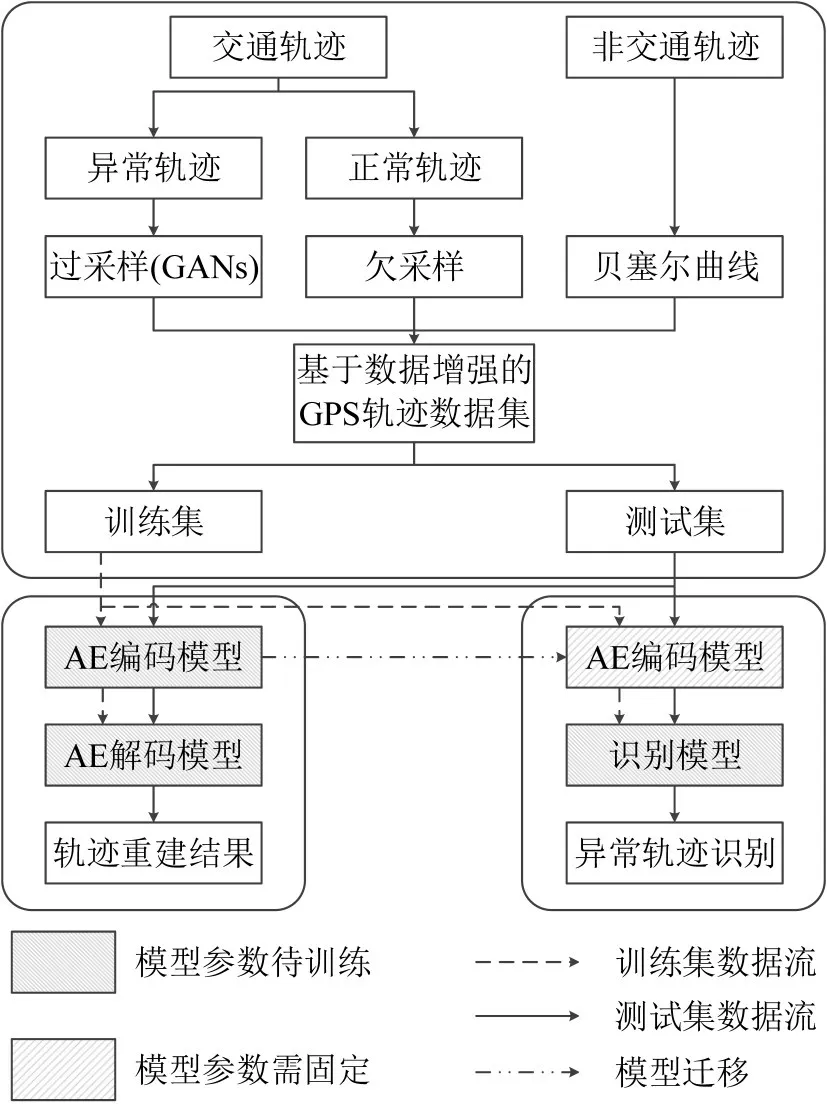
图2 基于数据增强的轨迹样本集构建和数据流向Fig.2 Trajectory dataset construction and data flow based on data augmentation

对抗生成网络GANs 是通过对抗学习逼近数据分布的生成模型。GANs由生成器G和判别器D组成，两者均为神经网络。G的目的是输出可欺骗D的人工合成样本，D的任务是判断样本是真实存在还是人工合成，两者不断对抗并在理论上达到纳什均衡。当模型训练完成后，G能产生骗过D的合成异常轨迹，G与D的目标函数为

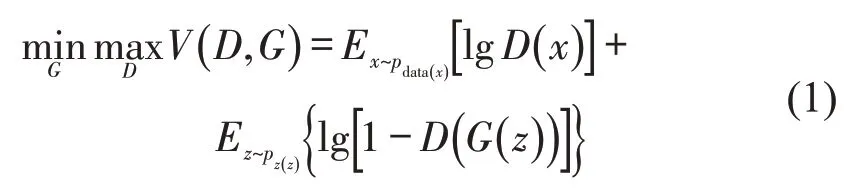
式中：x为从现实的异常轨迹分布pdata(x)中采样得到的异常轨迹；z从概率分布pz(z)(一般为均匀分布)中随机采样得到，喂给G产生合成的异常轨迹G(z)。模型训练D使x和G(z)分别被识别为1和0，使G生成G(z)并期望D[G(z)]的值为1。

对异常轨迹数据通过GANs 进行过采样的训练过程如图3所示。

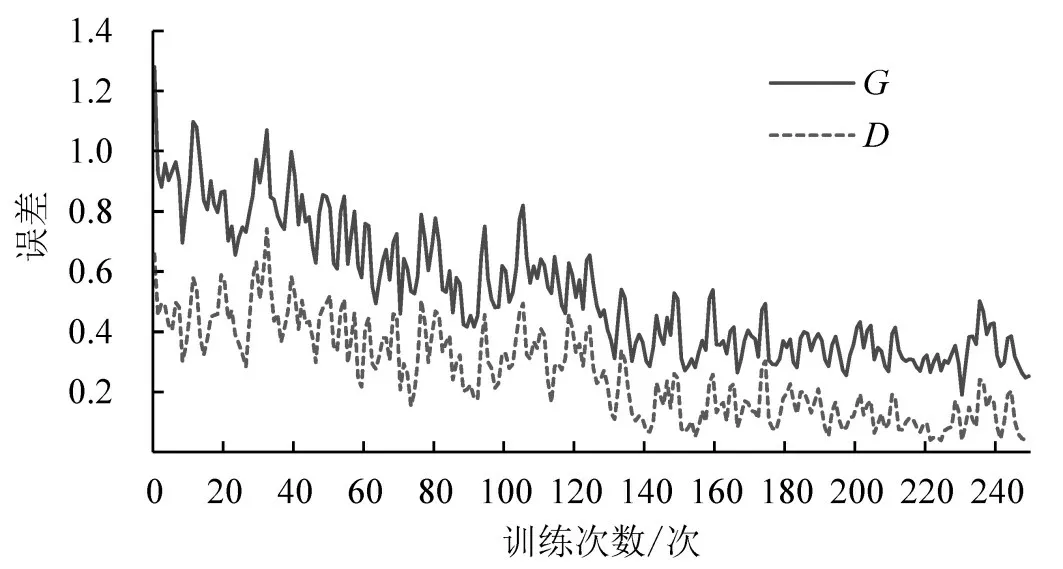
图3 对抗生成网络GANs生成器G和判别器D的训练过程Fig.3 Training process of Generator G and Discriminator D for GANs

图3中G和D的损失值在相互博弈中浮动下降，随着训练次数的增加，G和D的损失值逐步趋于稳定，此时，便可以使用生成器G产生人工合成的异常轨迹。

本文使用贝塞尔曲线生成非交通轨迹。对于每条曲线，首先，产生随机数u∈[5,30]作为控制点；然后，生成贝塞尔曲线方程；最后，等间隔采集曲线坐标得到非交通轨迹。u阶贝塞尔曲线通过控制点生成平滑曲线为

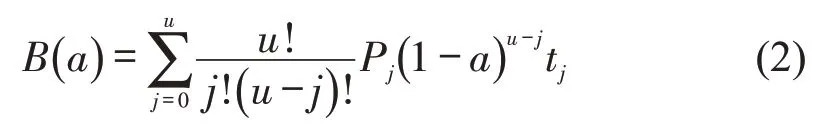
式中：曲线自变量a的定义域为0～1；Pj为曲线的控制点坐标；u为贝塞尔曲线的阶数。综上，本文通过数据增强将样本集扩展为{(Tk,lk)|lk∈{0,1,2} ;k=1,2,…,N}，标签lk取值0，1和2 分别对应正常交通轨迹，异常交通轨迹和非交通轨迹。

2.2 LSTM-AE-Attention模型设计

LSTM-AE-Attention 模型包含AE 神经网络和预测网络两部分。LSTM-AE是由编码器和解码器组成并添加LSTM的AE 神经网络，负责捕获特征并输出重建轨迹；预测网络，在接受LSTM-AE的预训练特征后，结合Attention进行异常识别。计算流程如图2所示，先训练和测试轨迹重建的效果，再固定AE编码器的参数用于异常轨迹识别。

(1)LSTM-Autoencoder结构

自编码网络(AE)是提取特征的无监督算法，由编码Q1和解码Q2组成并融合LSTM 成为LSTMAE。编码将Tk映射为长度为d的向量c=[c1,c2,…,cd]；解码将向量c映射成同Tk维度相同的序列。LSTM-AE的优化目标是使输入和输出的差值不断降低，当训练完成后可认为c蕴含了Tk的特征。

Q1和Q2由数个LSTM 组成，为保证特征留存和传递，LSTM有3个函数，分别为输入门g遗忘门f和输出门o，3个函数共同更新LSTM的状态，计算公式为

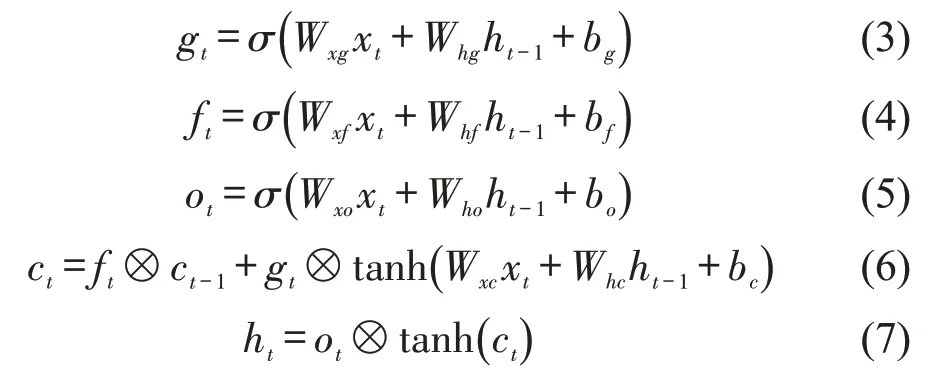
式中：gt，ft和ot分别为第t层输入门，遗忘门和输出门的函数输出；ct和ht作为当前层提取的信息保留并向下层传递；Wxj，Whj和bj为LSTM的参数，j∈(g,f,c,o)；σ(⋅)和tanh(⋅) 为relu和tanh 函数；⊗为元素乘法运算符。神经网络模型框架如图4所示。

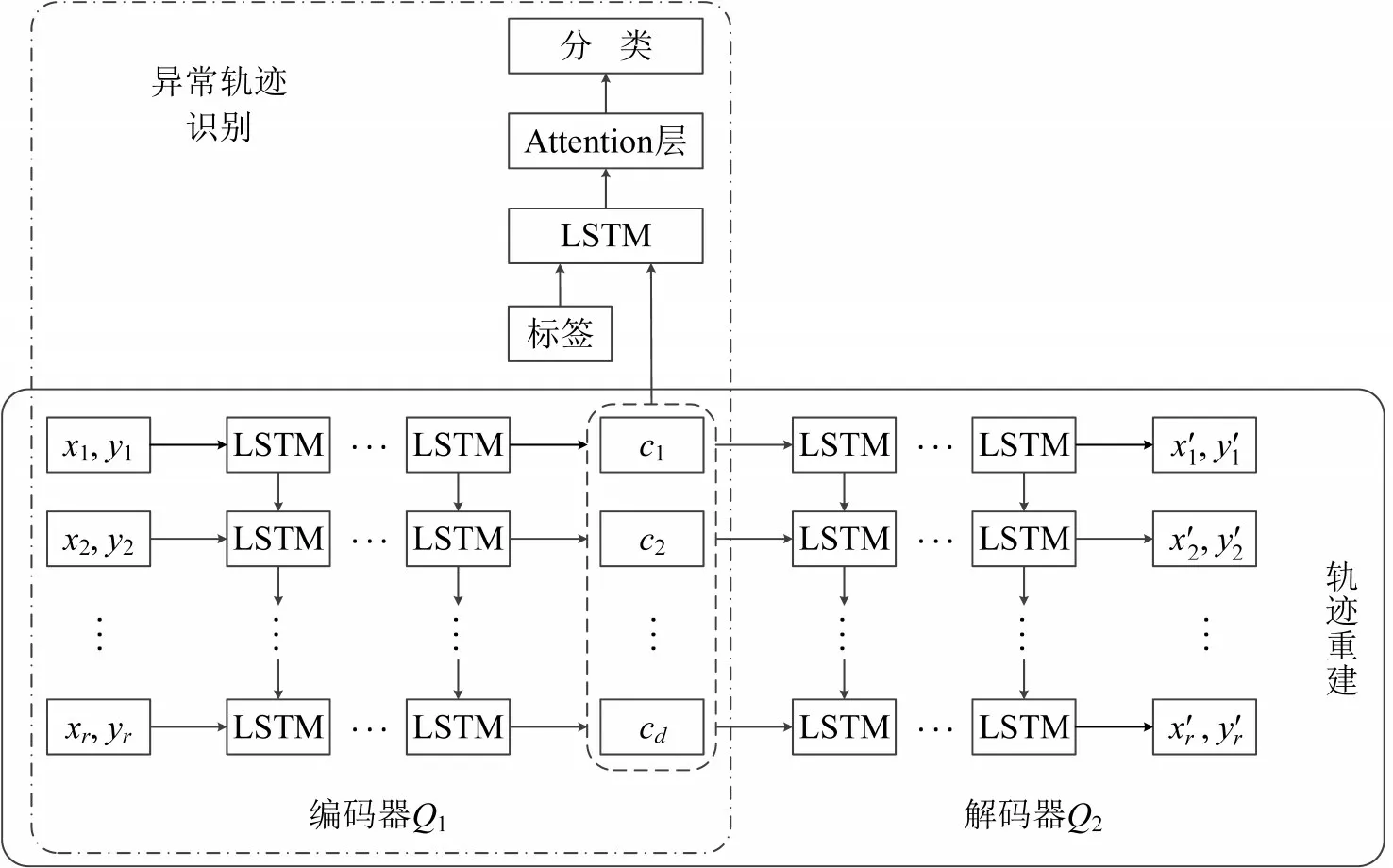
图4 LSTM-AE-Attention神经网络模型结构Fig.4 Structure of LSTM-AE-Attention neural network model

(2)基于注意力模型的异常轨迹识别

图4中异常识别部分，注意力模型由单层LSTM和Attention 层组成。注意力模型扫描向量c=[c1,c2,…,cd]得到需要关注的焦点后对其投入更多权重，在获取细节的同时抑制不重要的信息。Tk经过F1的映射后得到向量c，而后实现Attention层，计算式为

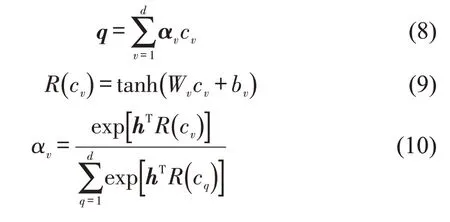
式中：q为经过编码器Q1提取得到的特征向量c在权值α的加权求和，并作为特征向量用于轨迹异常识别。具体地，全连接层R(cv) 以参数Wv和bv实现cv的非线性映射，而后通过Softmax 函数计算cv的归一化权重αv。其中，Wv，bv和h被赋初值并随着训练不断被更新。

3 实验及分析

3.1 数据来源和实验设计

本文使用北京市2015年1月12日-18日采集的出租车GPS 轨迹数据，经过清洗后有10400 条。将可视化后的轨迹进行人工标注，得到异常轨迹803条，异常轨迹占数据集的8.0%。数据增强后得到正常交通轨迹1800条，异常交通轨迹1200条，非交通轨迹1200 条，在避免过度的欠采样丢失正常交通样本的特征，同时维持正常交通轨迹数量多于异常交通轨迹的前提下，样本数量基本达到均衡。取数据集的80%为训练集，20%为测试集，两个数据集的标签比例均衡。

为验证模型有效性，实验设计有LSTM-AEAttention 模型组件对比、轨迹重建和异常轨迹识别，将本模型与其他模型通过评价指标进行对比分析。全连接层(MLP)，门循环单元(GRU)，支持向量机(SVM)和随机森林(RF)被运用在实验中，评价指标和对比模型如表1所示。

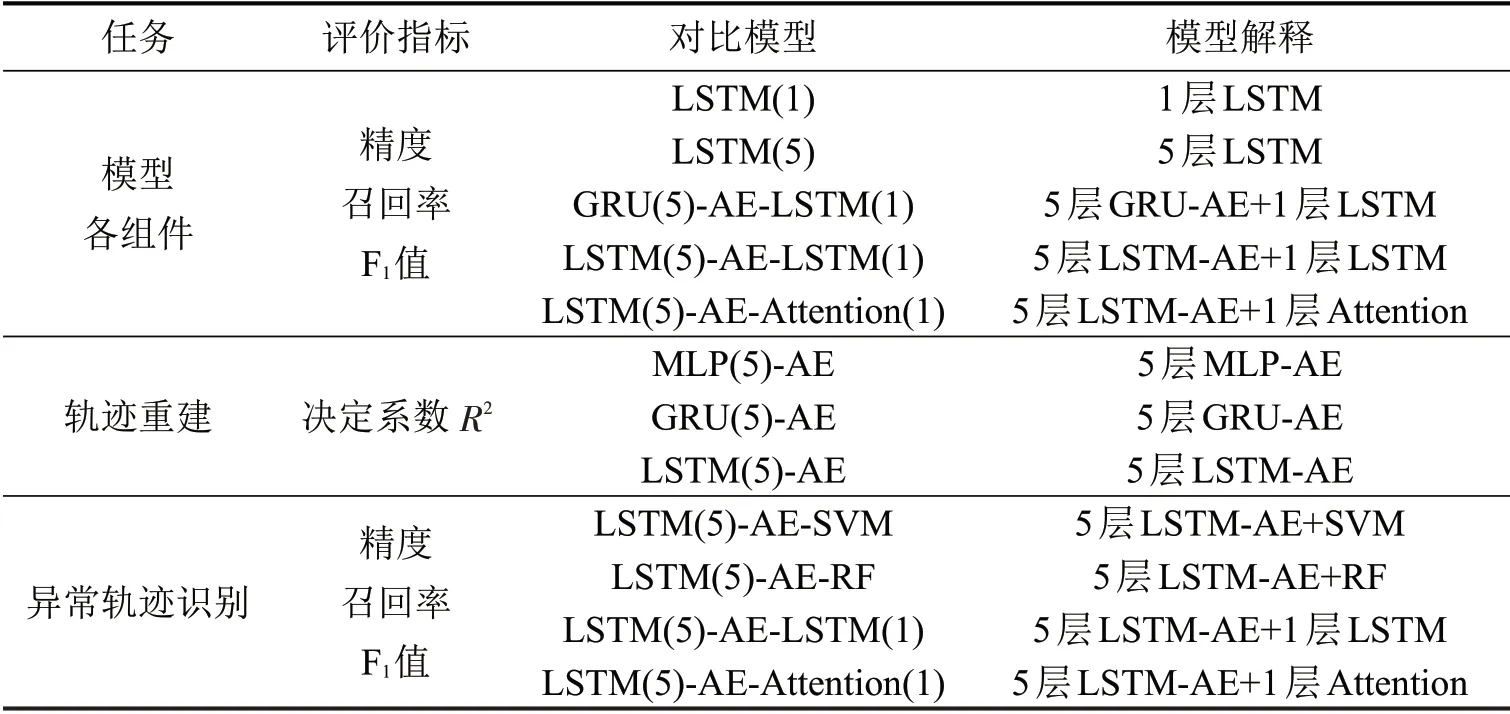
表1 实验设计Table 1 Experimental design

用决定系数R2评价轨迹重建效果，这里以经度为例，第k条轨迹Tk经度方向的决定系数公式为

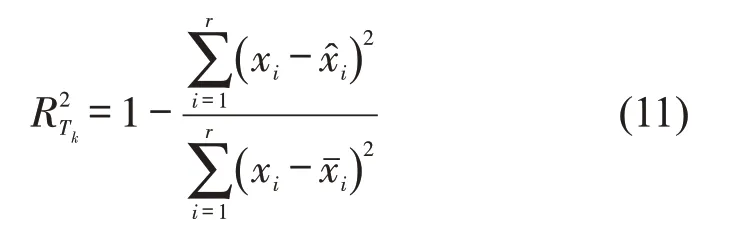
式中：r为轨迹Tk中点的数量；xi为轨迹Tk第i个经度坐标；为对应预测的经度坐标；为xi的平均值。R2越接近1，表示重建效果越高；反之，则低。

为重点对比模型在判别异常交通轨迹上的性能，本文将识别结果归为异常交通轨迹(正类)和正常及非交通轨迹(负类)两类。统计结果中包括：真阳性样本、假阳性样本和假阴性样本，真阳性样本是实际和预测均为正类，假阳性样本是实际为负类而预测为正类，假阴性样本则是实际为正类，预测为负类。通过上述样本计算精度、召回率和F1值，公式为

式中：STP、SFP和SFN分别代表真阳性样本、假阳性样本和假阴性样本的数量；eprecision为精度，指模型识别为异常轨迹的样本中真正是异常样本的比例；erecall为召回率，指全部异常轨迹中，被模型正确识别出的比例。若模型只成功识别出1 个异常轨迹而其他样本均非异常，精度为1 但召回率很低；若模型将所有轨迹都识别为异常，召回率为1但精度很低。因此，凭精度或召回率无法评价模型的性能，本文增加F1值综合评价模型性能，其值同时受精度和召回率的影响。

3.2 数据来源和实验设计

GANs通过MLP构建，其中，G由神经元个数为256、512和1024的MLP 构成；D由神经元个数为512和256的MLP 构成。LSTM-AE-Attention采用5 层LSTM 结构，每层神经元的个数为64、32、16、32和64，激活函数为relu 函数，同时为避免过拟合，层与层之间使用Dropout层。为保证一致性，层数为5的AE 模型(MLP-AE，GRU-AE和LSTMAE)的神经元个数与LSTM-AE-Attention的设置相同。层数为1的LSTM神经元个数为64，其他超参数与Attention-LSTM-AE中LSTM模块的设置保持一致。此外，为保证结果可靠，挑选SVM和RF 中典型1～2 个超参数进行网格搜索，例如：SVM的惩罚系数，RF中树的数量和最大深度。

模型采用Python 编写，基于Tensorflow和Keras 实现并使用GPU 加速。数据进行了中心化。轨迹重建的损失函数为均方误差(Mean Square Error，MSE)，异常识别的损失函数为交叉熵损失函数(Cross Entropy Loss，CEL)，即

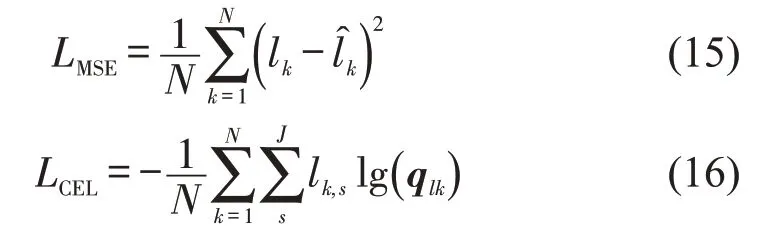
式中：li和为第i个样本的真实值和预测值；N为样本数量；J为类别数量；lk,s为指示变量，即当lk属于类别s时为1，否则为0。qlk为q的第lk个分量。模型的优化器均为Adam，学习率在0.00001～0.001 寻优后，GANs的学习率为0.0005，轨迹重建的学习率为0.0005，异常识别的学习率为0.0001。批量大小在1～32寻优后均设置为16。迭代次数为50 次，神经网络在训练中采取早停法，使模型获得较好的泛化能力。

3.3 模型结果对比分析

(1)模型各组件对比分析

通过LSTM-AE-Attention的各部分进行拆分实验，从多种评价指标体现模型各模块的贡献。LSTM-AE-Attention 模型优化实验结果如表2所示。

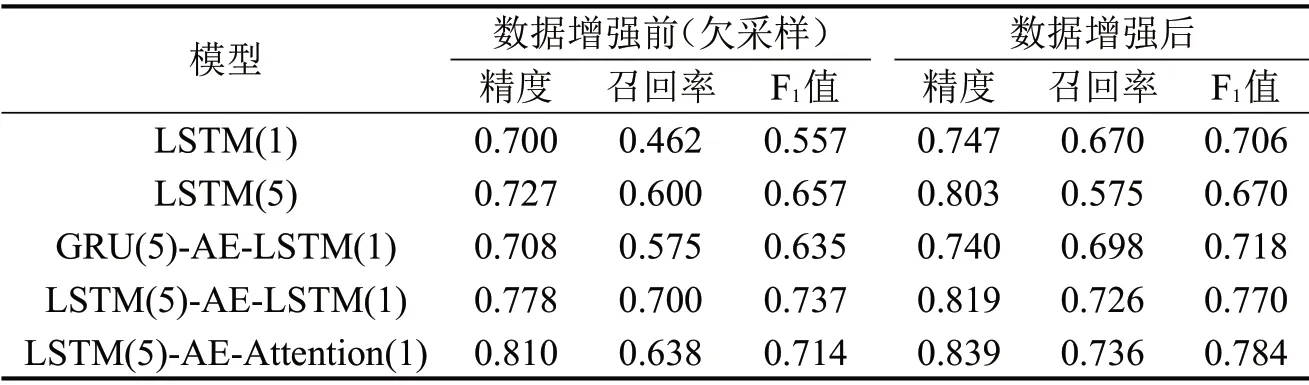
表2 LSTM-AE-Attention模型优化实验结果Table 2 Experimental results of LSTM-AE-Attention model components

由表2可知，数据增强后模型的精度、召回率和F1值均有提升，其中，精度的提升范围为3.5%～10.4%；召回率的提升范围为-4.1%～45.0%；F1值的提升范围为1.9%～26.0%。精度提升幅度低于召回率的提升幅度，说明模型在没有盲目将所有轨迹识别为异常的前提下提升了各项指标。

数据增强后，使用AE模型的精度、召回率和F1值的平均值分别为0.799、0.720和0.757，比不使用AE提升了3.1%、15.7%和10.0%，说明是否使用AE对于模型性能有明显提升。对于LSTM-AE-Attention，3项指标均优于其他模型，F1值比数据增强前提升9.8%。AE能有效提升模型对异常轨迹的识别精度，后续均采用AE进行实验。

(2)轨迹重建对比分析

为进一步对比轨迹重建，将样本按轨迹点数量等距划分为6类，用MLP-AE，GRU-AE和LSTMAE这3个模型进行重建并对比6类样本的重建效果(包括经度和纬度方向)，重建模型指标如表3所示。

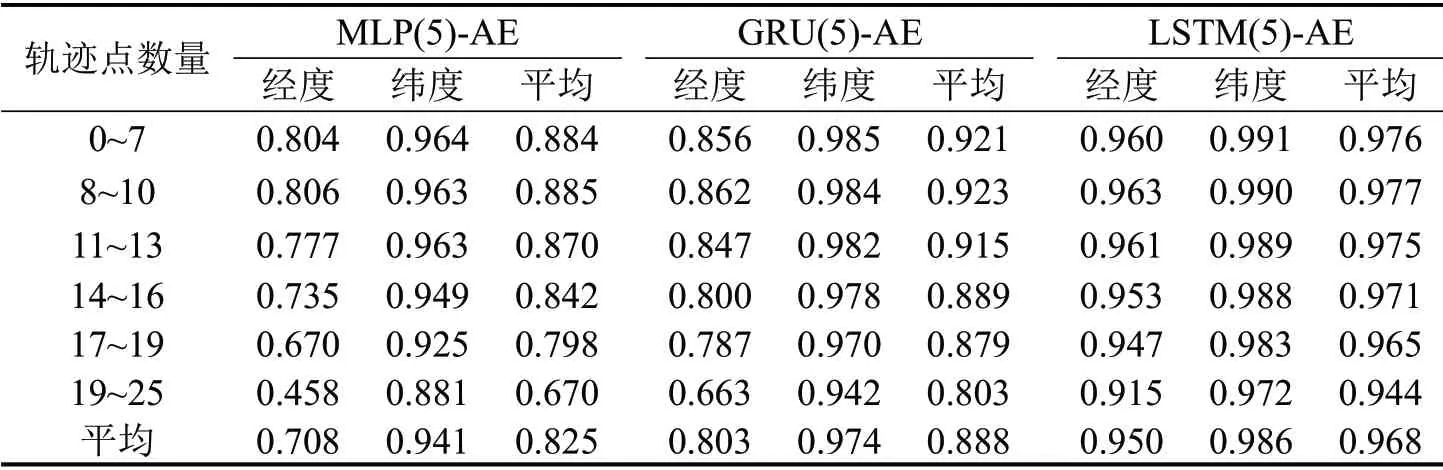
表3 MLP-AE、GRU-AE和LSTM-AE轨迹重建模型指标Table 3 MLP-AE,GRU-AE and LSTM-AE trajectory reconstruction indicators

3个模型的平均决定系数均在0.8 以上，重建精度较高，说明AE对于轨迹重建是有效的。MLPAE的平均决定系数为0.825，低于GRU-AE和LSTM-AE，LSTM-AE的平均决定系数最高为0.968。经度比纬度的决定系数要低，3个模型得到相近结果。

轨迹点数量小于16的样本，3个模型的平均重建精度高于0.8，而轨迹点数量在17 个以上的样本，MLP-AE 经度的决定系数低于0.7；而LSTMAE无论轨迹点数量多少，其决定系数仍保持在0.9以上，说明LSTM-AE在重建方面有较强的稳定性，适用于不同轨迹点数量的样本。

MLP-AE、GRU-AE和LSTM-AE的轨迹重建对比如图5所示。

由图5可知，LSTM-AE的重建效果比GRU-AE和MLP-AE 好，说明AE 结合LSTM 后编码和解码过程在处理序列数据时更具优势，重建后的结果修正了轨迹坐标，使曲线更加平滑。

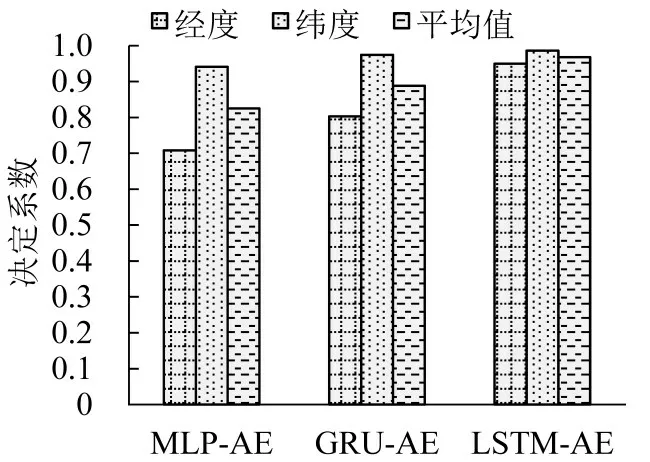
图5 MLP-AE、GRU-AE和LSTM-AE的轨迹重建模型对比Fig.5 Comparison of MLP-AE,GRU-AE and LSTM-AE model on trajectory reconstruction

(3)异常轨迹识别对比分析

在AE 框架下，对比SVM、RF、LSTM和Attention 这4 种模型在异常识别任务里的表现，结果如表4所示。

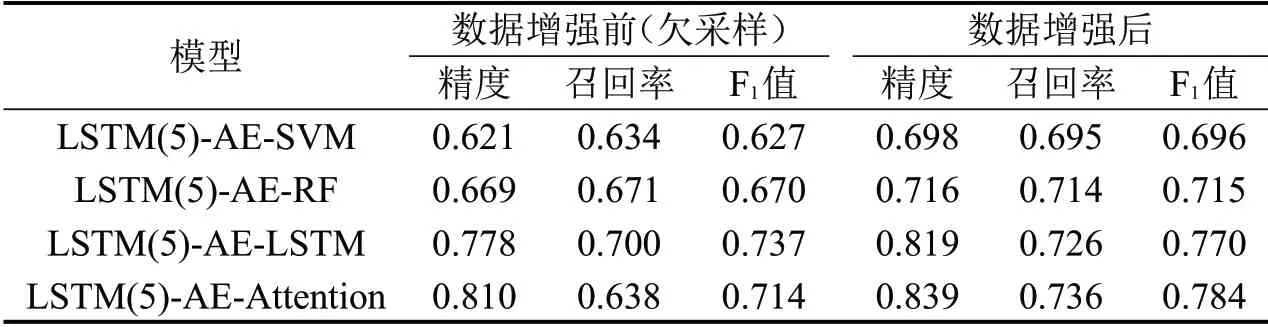
表4 不同预测模型对比Table 4 Comparison of different prediction models

数据增强后，模型的评价指标有不同程度的提升，F1值提升幅度为4.5%～11.0%；无论数据增强前、后，4个模型的精度均高于或接近召回率，说明模型在保证召回率的同时，倾向于将轨迹精准地识别为异常，能有效避免异常轨迹被遗漏；LSTM和Attention的性能均优于SVM和RF，而Attention 在数据增强后较其他3个模型F1值提升范围为1.8%～12.6%。

数据增强前、后，不同模型在测试集下的混淆矩阵对比结果如表5所示。

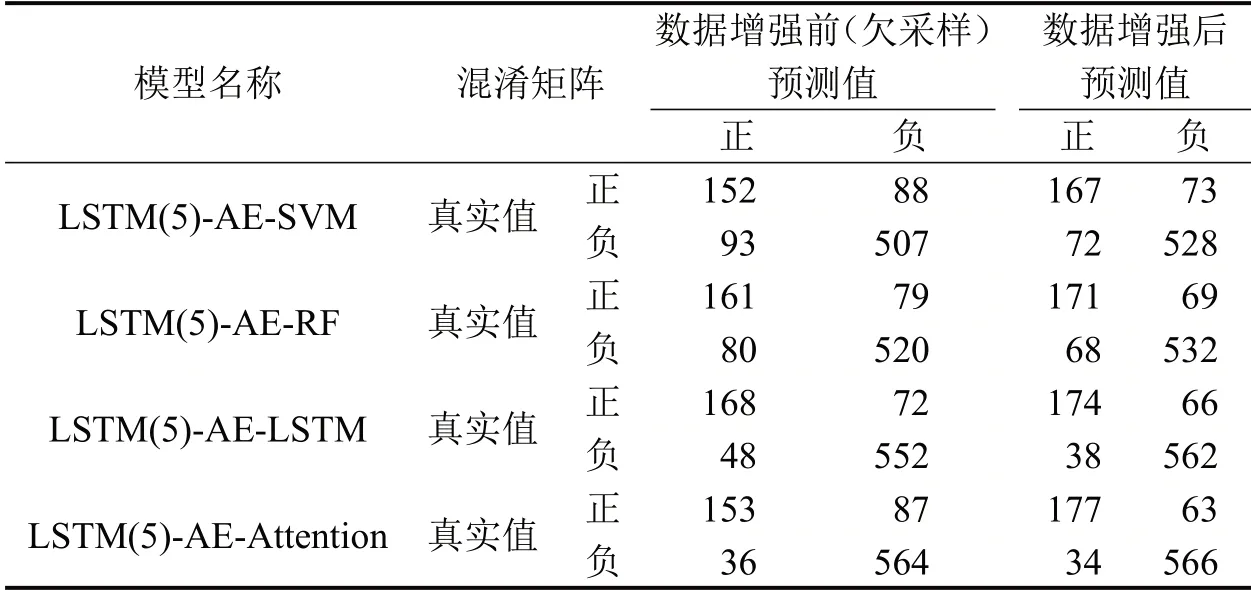
表5 不同预测模型混淆矩阵对比Table 5 Comparison of confusion matrix of different prediction models

由表5可知，数据增强后模型可将更多异常轨迹正确分类，真阳性样本的数量平均提升了8.7%；数据增强后模型也降低了错误分类的数量，假阳性样本和假阴性样本分别平均降低了21.2%和20.2%；相较于其他模型，Attention模型将异常轨迹判断为其他轨迹的数量最低，正确分类(即真阳性样本和真阴性样本)的数量最多且占测试集的88.5%。

4 结论

本文构建基于数据增强的LSTM-AE-Attention模型，针对轨迹重建和异常轨迹识别两个问题进行实验，主要结论如下：

(1)提出移动轨迹数据集的数据增强流程。将样本集中正常交通轨迹和异常交通轨迹的比例由12∶1 进行均衡，使正常交通轨迹、异常交通轨迹和非交通轨迹的比例达到1.5∶1.0∶1.5，将异常轨迹识别实验中模型的F1值提高9.8%。

(2)使用LSTM-AE模块重建轨迹。实验表明，该模型的平均决定系数为0.968，且当轨迹点数量大于17 时，该系数仅下降0.5%。模型在轨迹点数量较多时仍可保证重建效果的稳定性。

(3)通过LSTM-AE-Attention 模型识别异常轨迹。在LSTM-AE 参数预训练的基础上嵌入Attention模块，使模型的F1值平均提升了7.8%。相较未使用AE的模型，该模型的精度、召回率和F1值分别提升了3.1%、15.7%和10.0%。模型能够保证异常轨迹识别的可靠性。