基于数据驱动的机场水泥混凝土道面性能退化预测

魏保立，郭成超，邓苗毅

(1.郑州大学，水利科学与工程学院，郑州450001；2.郑州航空工业管理学院，土木建筑学院，郑州450046；3.中山大学，土木工程学院，广东珠海519082)

0 引言

机场跑道是机场基础设施中功能重要、养护维修投入最多的结构之一，因此机场道面性能状况一直是机场设施运维部门最关注的问题。通过道面性能预测，可以对养护维修决策提供指导，有助于将道面性能维持在适当水平，故长期以来道面性能退化过程的预测都是机场道面领域研究的重点。

20世纪中叶，机场管理部门对于机场跑道的运维基本停留在“头疼治头，脚病医脚”的事后维护阶段。事后维护[1]是基于病害的维护方式，即在跑道出现损坏的情况下进行维护。这种维护方式是在损坏出现时才采取维护措施，而这些损坏会对机场运营造成巨大的经济损失。21世纪初期的近10年，为减少损坏出现频率，管理者摒弃了被动式的事后维护方式，采取较为积极的预防性维护。预防性维护是基于时间的维护方式，即按照时间确定维护周期，在固定的时间对跑道进行维护，以确保跑道在未来一段较长的时间内可以正常运营。但是，基于时间的维护会造成跑道养护的不均衡，即整个跑道一致的维护周期会造成某些道面区域进行不必要养护，而某些道面区域不能及时得到养护。且预防性维护依赖于技术人员的经验，缺乏数据支持。

目前，在很多行业尤其是工业界发展起来的预测性维护(Predictive Maintenance，PdM)是智能维护的一种典型方式，预测性维护[2]是数据驱动的维护方式，它融合了传感器技术、信号处理技术等，综合运用可靠性分析、统计学、机器学习等方法，发现潜在的病害，从而制定更加合理有效的维护计划。

因此，本文通过国内外关于机场道面性能退化预测方面的资料调研和收集，从地方机场定期检测数据中提取样本，建立机场道面性能退化预测模型，为机场跑道预测性维护提供技术支持，同时也为合理部署机场跑道的维修和养护计划提供借鉴参考。

1 机场道面性能退化模型的建立方法

1.1 非线性混合效应模型

考虑国内外道面(或铺面)性能衰变方程，结合道面性能衰变模型应能反映道面的行为和道面性能特点的要求，确定选用一个通用方程作为描述道面结构行为的基本方程，即《民用机场道面评价管理技术规范MH/T 5024-2019》中道面性能衰变方程[3]，具体形式为

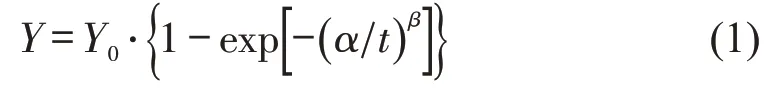
式中：Y为道面性能指数(可以是道面状况指数PCI、道面质量指数PQI或国际平整度IRI等指标)；Y0为某时刻道面性能指标的数值，一般为道面开始投入使用时性能指标初始值，多采用100 标量表示；t为道面的使用时间；α、β为衰变方程的模型参数，与个体特征变量有关。

不同机场道面结构的性能衰变曲线均可由式(1)确定，其曲线形状主要由参数α、β控制，任何一个复杂的道面性能曲线与α、β存在着一一对应关系，可用二维点(α、β) 来描述道面性能的衰变历程，得出反映机场道面使用性能发展变化规律的退化曲线，并可以进一步定量分析研究道面使用性能的退化过程。同时也可以得出一个重要推论，所有影响道面性能的因素都将影响参数的大小，即α、β可以表示为：α=f(交通轴载，结构强度，面层厚度，基层类型，环境状况，材料类型)；β=f(交通轴载，结构强度，面层厚度，基层类型，环境状况，材料类型)，其中，f(∙)为目标函数。

由于机场道面使用性能的退化具有复杂性、多样性和随机性的特征，因此，需要在一定的随机扰动假设下，尽量找出最简单的模型形式，并为数据提供良好的模型拟合。结合国内外研究成果，本文选用的机场跑道个体预测模型为

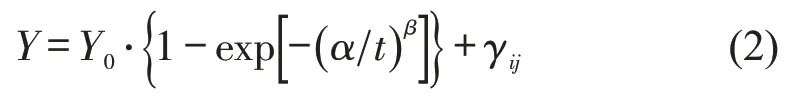
式中：γij为随机正态残差项。

由于所有影响道面性能的因素都将影响参数α、β的大小，通过探索性分析，将个体模型测量参数进行组合，得到群体结构模型为

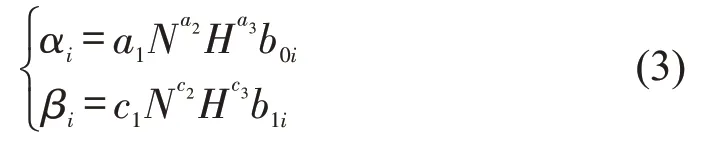
式中：N为航空交通量；H为道面结构厚度(cm)；αi、βi为个体模型参数，是正态随机变量；ai和ci为固定效应参数；bji为随机效应。对式(3)进行对数变换，转化为线性表达式为

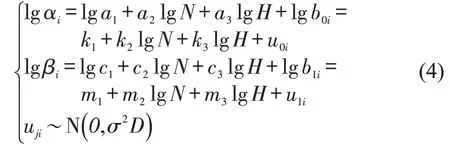
式中：ki和mi为固定效应参数；uji为服从均值为0，方差为σ2D正态分布的残差。

1.2 联合估计方法

在利用多个数据源进行参数估计时，联合估计方法是一种首选的统计方法，因为联合估计不仅可以确定所有数据源中共有的解释变量，还可以确定每个数据源中特有的解释变量[4]。联合估计方法最早被Morikawa 等[5]用于旅行需求建模，Archilla[6]、Prozzi[7]和Anastasopoulos[8]用联合估计方法对路面性能进行了评价或分析预测。

考虑两个不同的数据源A和B，两个数据源都包含因变量PCI(本文研究对象)，几个影响因素(解释变量)如飞机起降频次、道面结构厚度等，具体到每个数据源的数据模型为

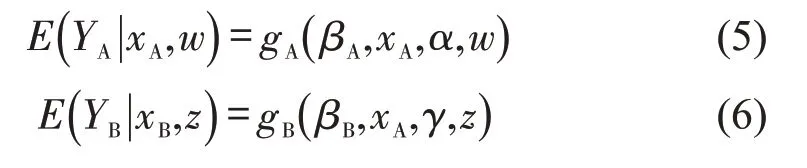
式中：E(⋅ |⋅)为PCI的条件期望函数，函数形式为g(⋅)；YA、YB分别为模型A、B的PCI；xA、xB分别为模型A、B 共有的自变量；w为仅与模型A 相关的自变量；z为仅与模型B相关的自变量；βA、βB分别为与模型A、B有关的参数；α、γ分别为与w、z有关的模型参数。

根据解释变量的不同特点，一般情况下：βA≠βB，因此，两模型参数集的第i个元素之间的关系可以表示为βAi=βBi+δi或βAi=μi βBi，其中，δi和μi为偏差参数或称为偏差纠正系数，通过联合估计方法可以获得δi和μi的估计值，从而确定两个模型的参数值。由于联合估计方法融合了多种数据源，模型的总体样本量较大，使函数参数估计值的方差较小，模型的统计效率较显著。在机场道面评估模型中采用联合估计法的偏差系数，不仅可以考虑飞行交通量lgN和道面厚度lgH在不同样本的差异，还可以考虑不同数据集之间未观察到的异方差。

2 机场道面数据集的整理

机场道面历史数据是建立机场道面性能退化预估模型的基础，本文以两组不同特点的机场道面测试历史数据为数据源。数据集1 为我国民用机场道面PCI现场测试历史数据集，其特点和详细信息参见文献[9]；数据集2为河南地方机场跑道和滑行道2007-2017年现场测试数据集，本文对其进行简要介绍。

数据集2 是河南地方某机场2007，2013，2017年飞行区跑道、滑行道道面的检测时间序列数据。至2019年，该机场飞行区道面已使用22年，飞行区道面已接近其设计使用寿命。为了全面掌握飞行区道面综合情况，以便为制定该区域道面近期的管理和改造计划提供依据，机场管理部门于2007，2013，2017年分别对机场飞行区跑道、滑行道和联络道道面进行全面检测，并对现场检测数据进行综合分析形成较高价值的数据库。

为尽量避免数据预处理过程中产生新的误差，根据文献[9]中数据源的特点及数据处理方法。将河南地方机场道面结构相同年起降次数基本类似的道面区域和相同道面结构构成的个体划分为组，假设组内PCI数据具有同质性，依靠道面个体在观测时间点上的差异，通过“时间推移”延长组内数据的时间序列，同时剔除部分较特殊或有疑义的个体数据，最后得到91组刚性道面数据，其中部分数据如表1所示。

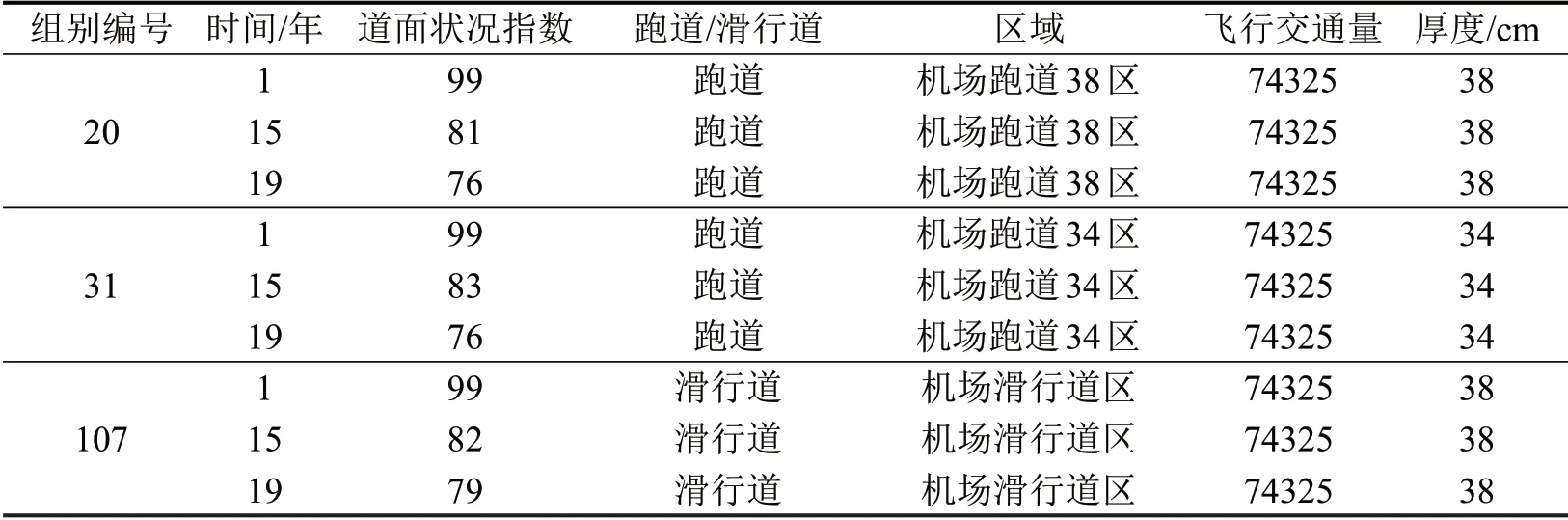
表1 机场道面历史数据源内容简表Table 1 Summary table of airport pavement history data set content

3 预测模型的参数估计

结合机场跑道性能退化特点，对式(1)进行变换，即

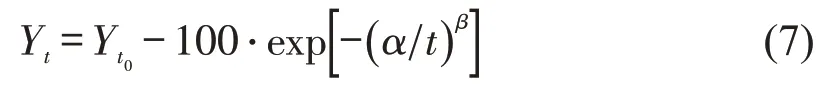
式中：Yt为t时刻机场道面的状况指数；Yt0为初始时刻t0时机场道面的状况指数，数值大小和机场道面结构类型，飞行交通量等影响因素有关，数值一般在90～100范围之内。为了说明混合效应模型的有效性，在进行建模之前，首先按照式(7)，在不考虑混合效应的前提下，采用非线性回归方法得出机场跑道性能退化预测模型的参数值；同时利用飞行交通量N和道面水泥混凝土面层厚度H两个变量捕捉期望函数中α、β的异方差，为了便于分析，分别以N和H的对数作为解释变量引入函数之中。

3.1 非线性普通回归模型参数估计

通过探索性建模，将所有可能对整个数据样本的PCI值有影响的变量纳入模型，经过分析剔除所有不具统计学意义的变量，显著性水平为10%，得到采用联合估计法的拟合模型。为便于区别，将此模型标记为模型Ⅰ，表达式为

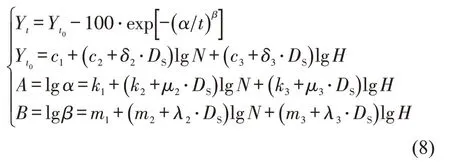
式中：δi、μi、λi为联合估计法的偏差系数；DS为数据集指示变量，取值为0 或1。最终建立的模型Ⅰ包括15个参数，结果如表2所示。保留在模型中的这些参数，可以分析偏差参数，也可以进一步分析模型中解释变量对PCI变量的影响。

虚拟变量DS根据数据集不同，取值为0 或1，则对于每个数据源，模型I 中参数的数量也不相同。以数据集1为例，其DS取值为0，则表2中的偏差系数δi、μi、λi和DS=0 相乘以后数值为零，即偏差系数在数据集1 中均不存在，所以对于数据集1 来说，其参数数量减少到9 个。另外对于数据集1来说，将其做为对照数据集(或称基线数据)，数据集2 利用偏差系数来解释本身数据对于基线数据的潜在差异。

从表2可以看出，采用联合估计方法并纳入解释变量lgN和lgH后，非线性回归拟合模型的残差均方值较小，模型决定系数R2=0.972，这说明联合估计方法对改善模型的拟合效果作用显著，并且能够对数据源的异方差和组间效应进行较好的解释。

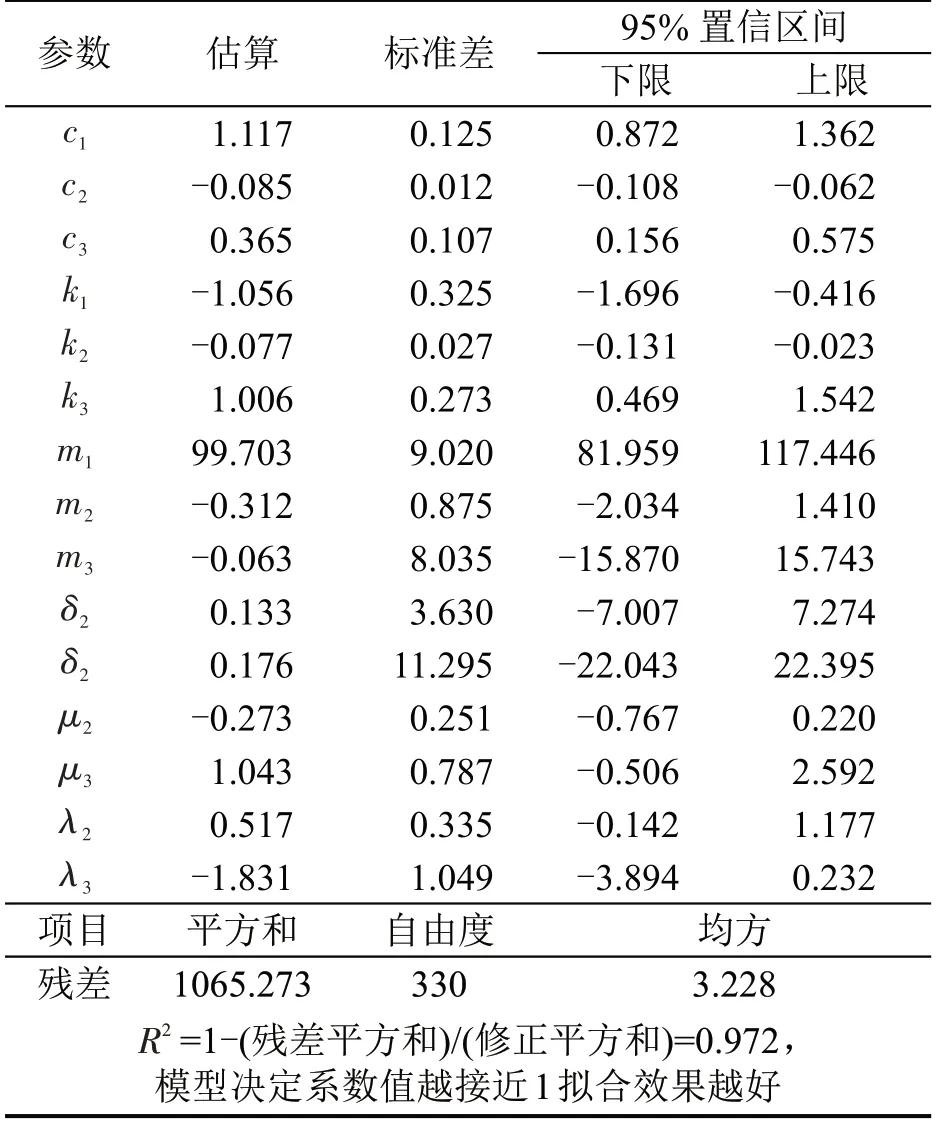
表2 非线性普通回归模型(模型Ⅰ)参数估计值Table 2 Parameter estimates for nonlinear ordinary regression model(model Ⅰ)

3.2 非线性混合效应模型参数估计

为了改善预测效果，进一步解释每个测试样本与总体均值的偏差，分析样本中未观察到的异质性。通过非线性混合效应得到预测模型(模型Ⅱ)，模型Ⅱ使用的参数和模型Ⅰ的参数变量数量一致，仅采用随机效应对模型Ⅱ参数进行修正，去除所有统计不显著的参数，重新评估其他参数的显著性，得到最终的非线性混合效应模型。经过探索性建模，最后得到非线性混合效应评估模型为

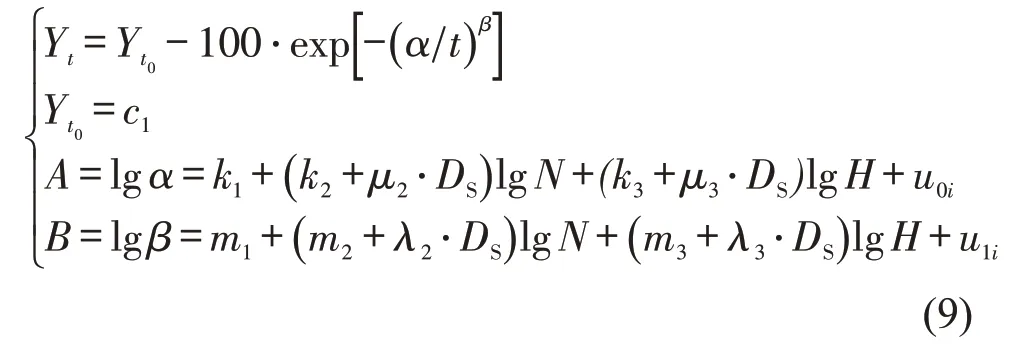
式中：uji为第i个数据集中第j个样本的正态随机误差。各参数结果如表3所示。

从表3可以看出，采用混合效应模型和联合估计方法并纳入解释变量lgN和lgH后，模型的标准差为1.565，较模型I的标准差3.228，减小比例约为52%；模型决定系数R2=0.989，回归拟合效果得到提高。说明混合效应方法对改善模型的拟合效果作用显著，能够对数据源的异方差和组间效应进行较好地解释。

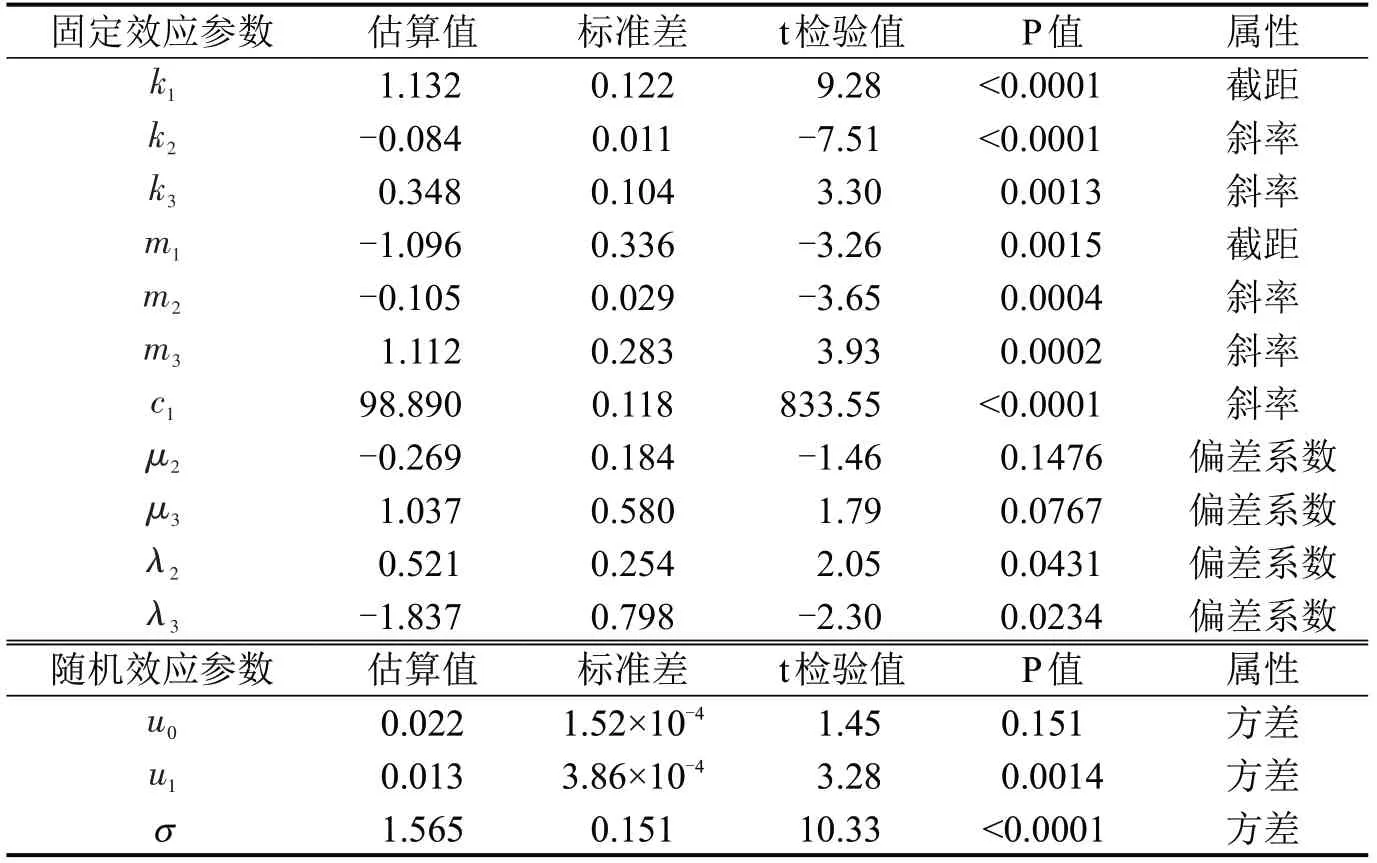
表3 非线性混合效应模型(模型II)参数估计值Table 3 Parameter estimates for nonlinear mixed effects model(model II)

为说明考虑随机效应和不考虑随机效应模型的差异，图1分别做出两个模型的拟合值和预测值。

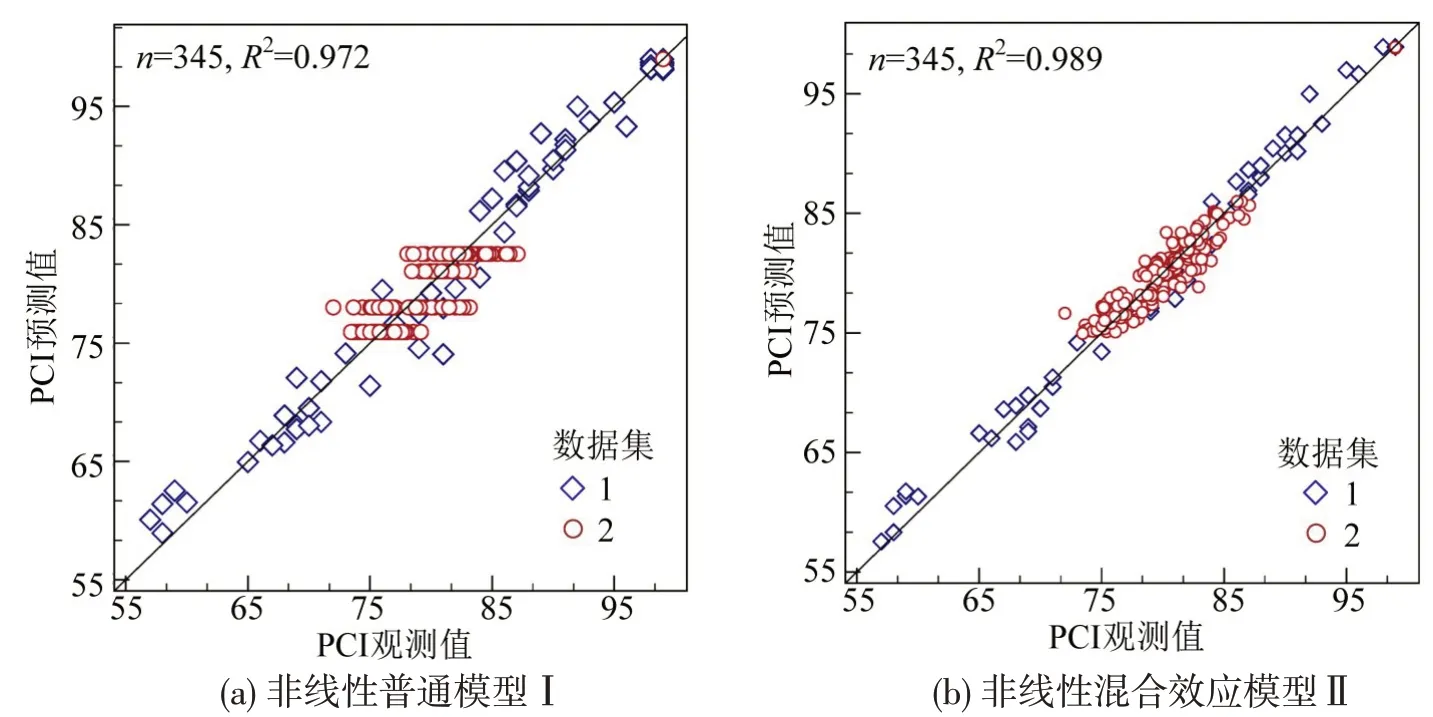
图1 PCI观测值和预测值对比Fig.1 Observed and predicted values of PCI

从图1可以看出，数据点比较密集的集中在45°对角线附近，值得注意的是在图1(b)中，对于数据集2，数据分布沿y轴分布更均匀，这说明包含混合效应的模型Ⅱ比无混合效应的模型Ⅰ对数据的解释要好。这主要是因为采用混合效应方法进行预测，模型预测的每个样本中都包含两个随机效应的因子(一个是α参数中的u0i，另一个是β参数中的u1i)，每个样本的误差可以被两个独立的随机误差进行解释，从而使混合效应模型的预测效果明显好于非线性普通回归模型。

4 模型预测性能分析

建模的目的不仅仅是找到一个数据拟合满意的统计模型，更重要的是建立一个具有结果可解释性的简约模型。下面对混合效应模型式(9)进行效果分析。

为了评价混合效应模型拟合不同交通水平的道面性能的预测效果，采用边际效应分析方法，即选取道面厚度相同，但不同交通水平的样本进行分析：选择数据集1 中样本S14(lgN=3.62)，样本S9(lgN=4.29)，样本S15(lgN=4.42)，样本S2(lgN=4.56)预测PCI，这些个体道面混凝土面层厚度均为32 cm，PCI 预测曲线如图2(a)所示。从图2(a)可以看出：混合效应模型对于不同飞行交通量水平(仅限于数据集中包含的飞行交通量范围)的道面个体均能较好地预测其PCI衰变趋势；混合效应模型预测曲线在t≤10年时，不同飞行交通量的道面PCI 基本相似，区别不明显，而当t＞10年以后，不同飞行交通量的道面PCI 衰变曲线有了明显差异；随着飞行交通量的增加，PCI的数值减小，并且飞行交通量水平越高，道面PCI的衰变速率越大。这说明随着飞机起降频次的增加，道面的损坏程度也在增大，导致PCI数值减小。

值得注意的是：在机场道面使用初期(图2(a)中所示为大概10年)，由于机场道面本身的结构或者材料特点，飞机起降频次的增加对于道面损坏影响较小；但是当机场道面使用时间大于一定年限以后，飞机起降频次的增加对道面损坏的影响较为显著。这说明飞机荷载对道面的损伤具有一定累积作用，具体是线性累积还是非线性累积需要进一步深入研究。

另外值得注意的是：飞行交通量lgN=4.29 与lgN=4.42的预测曲线基本重合在一起，说明这两种交通量水平的机场道面性能衰变趋势基本一致；然而，飞行交通量lgN=4.42 与lgN=4.56的预测曲线却差异显著，说明这两种交通量水平的机场道面性能衰变趋势明显不同。究其原因：由于本文是将飞机起降频次进行对数转换后，以其对数值进行分析，所以3 种水平交通量的对数值两两相差较小，4.42-4.29=0.13，4.56-4.42=0.14，但实际上3种水平的飞行交通量差异较大，差值约为6804架次，这可能说明在机场道面水泥混凝土面层厚度32 cm的情况下，飞机荷载作用次数达到一定的数量等级以后，机场道面性能衰变趋势将会发生突变。换而言之，也即是对于一定水平的机场等级(例如4F 机场)，其飞机起降频次有一个极限值，当飞机荷载作用次数超过这个极值以后，有可能对机场道面产生较为显著的损坏。这种推论只是对图2(a)所示的现象进行分析，结论可靠性如何还需要进一步研究。

为进一步评价混合效应模型拟合不同道面厚度等级的机场道面PCI 数值的性能，从数据集1 中按照残差较大原则选取具有相似交通量水平不同道面厚度值的样本S02(lgN=4.56，H=32 cm)、

S01(lgN=4.56，H=34 cm)、S08(lgN=4.65，

H=36 cm)和S06(lgN=4.65，H=40 cm)进行性能预测，结果如图2(b)所示。

从图2(b)可以看出：混合效应模型均能较好地拟合不同道面厚度等级的道面PCI(飞行交通量水平一定的情况下)，并且不同道面厚度等级的道面PCI衰变曲线差异明显。特点如下：随着道面厚度的减小，PCI的数值减小，且道面厚度越小，道面PCI的衰变速率越大。这说明随着道面厚度的减小，道面结构承受荷载的能力下降，导致机场道面在相同飞行交通水平下的损坏程度增大，PCI值也就越小。也间接说明混合效应模型对于不同道面厚度等级的道面个体均能较好的预测其PCI 衰变趋势。

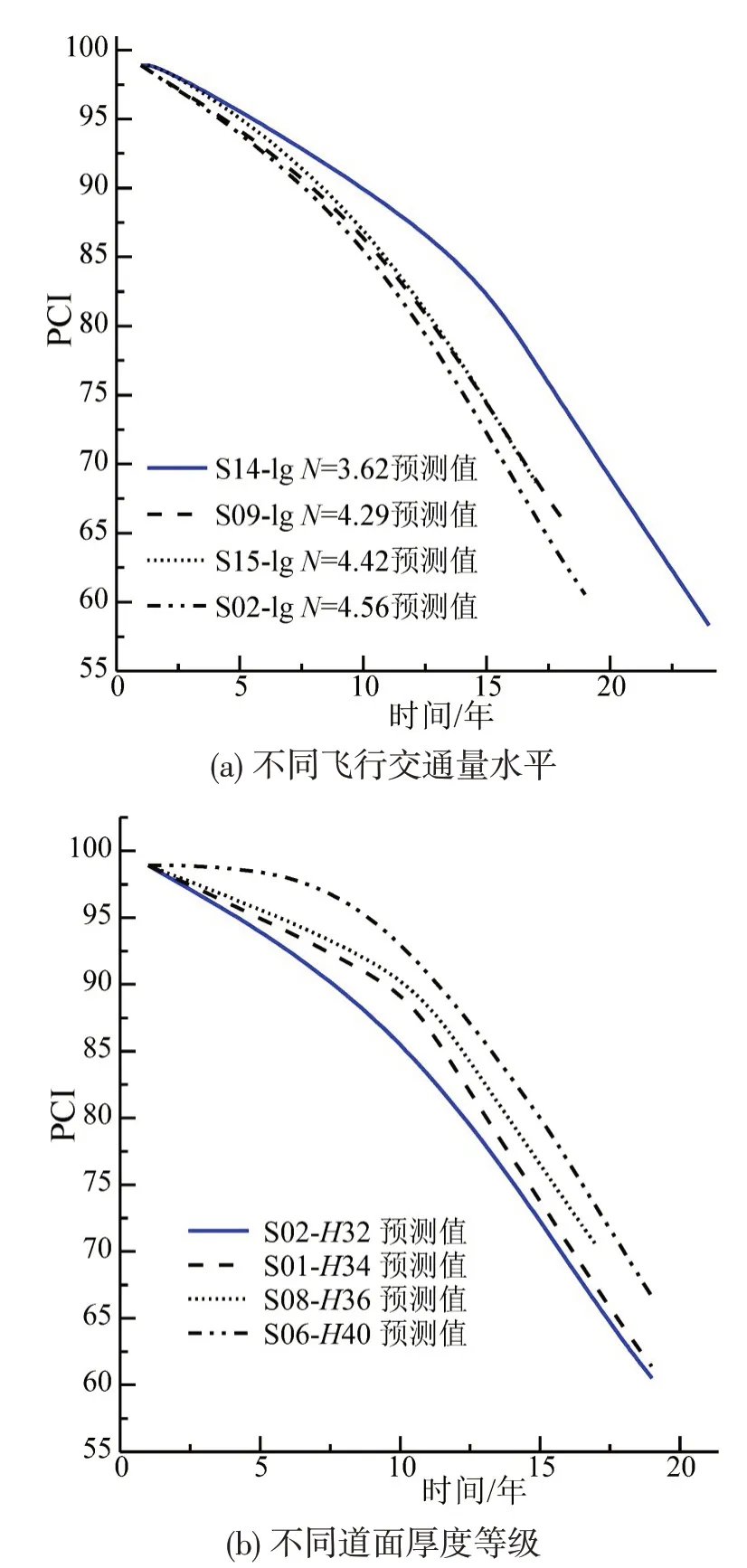
图2 不同水平的模型预测图Fig.2 Model prediction for different levels

5 结论

本文通过对两种机场道面性能检测数据的融合，集成了107组道面近30年的PCI数据来构建机场道面性能退化预测模型，以指示变量将两种数据集进行联合分析，通过参数分析和图形验证，指出不考虑混合效应时，非线性普通回归模型的拟合效果欠佳；采用混合效应方法并搭载联合估计技术建立预测模型，通过对混合效应模型的参数分析，阐明了混合效应模型的拟合效果显著。根据所建立的混合效应模型的参数估计结果，采用边际效应分析方法，对道面状况指数退化过程进行预测，评价了混合效应模型预测性能对飞行交通量和道面厚度的影响规律。

对地方民用机场道面性能退化过程的预测是优化机场道面运营策略规划的基础。在未来的研究工作中，如果能采集更多类型的数据(环境温度、湿度、道面材料种类等)，并综合考虑这些不同类型的影响因素对退化过程的作用，将对预测模型的精度和效果有较大提高。本文采用的数据融合只是涉及到数据挖掘的部分内容，对于其他的数据挖掘方法(比如深度学习、机器学习等)在机场道面性能退化过程预测的适用性和效果如何是未来的一个研究方向。