考虑边境站延误风险的中欧班列运输路径决策

吕敏，帅斌*，周照玉，张士行，左静，李林卿

(1.西南交通大学，交通运输与物流学院，成都611756；2.西南交通大学，唐山研究生院，河北唐山063000；3.兰州交通大学，自动化与电气工程学院，兰州730070；4.国家铁路局，市场监测评价中心，北京100036)

0 引言

中欧班列迈入高质量发展阶段，明确运输网络中薄弱环节的影响，选择更高效安全的运输径路将更能适应市场化国际物流运输需求，提高班列竞争力。目前，中欧班列运输路线决策研究考虑因素仍以时效性和经济性为主[1]，崔明阳[2]考虑货物时间价值建立时间和经济综合成本最小的优化模型，SEO 等[3]将风险因素引入路径选择，以多属性决策方法评估线路在货物完整性、运输安全性、通关便利性和信息交换便利性等方面的综合绩效。既有研究缺乏对中欧班列运输中边境站点的延误风险的关注。

目前中欧班列开行数量不断增加，而境外口岸能力短时间无法改善，边境站延误成为制约班列运营的主要障碍[4]。同时中欧班列境外段主要依赖国际货运代理，运输路径信息透明度低，难以有效控制运输风险和成本，边境站延误将在一段时间内成为托运人和班列运营者必须考虑的问题。本文基于对不同类型边境站延误时间特征的分析，提出基于期望损失理论[5]和货物时间价值[6]的边境节点延误风险测算方法，构建“风险-时间-费用”综合运输成本最小的中欧班列路径选择模型，为班列运营企业规避风险制定符合市场需求的路径方案提供辅助决策。

1 边境节点延误风险测算方法

边境节点延误是制约中欧班列高效运行的重要问题[4]，假设其延误时长t服从一定概率分布F(t)，货物价值损失与时间正相关。基于风险管理领域中期望损失[5]理论，将边境节点延误风险价值定义为中欧班列通过两国边境发生延误的货物损失期望，即

式中：E(Ti)为节点i的延误时间Ti的数学期望，其概率密度函数为fi(t)，t≥0，t=0 表示没有延误；csun为单位时间延误损失。

1.1 边境节点延误时间特征及概率分布

通常边境过境运输(Border Crossing)分为出口过境(Outbound)和进口过境(Inbound)。货物在出入口过境点均需要办理海关检查、安检和列检等各项检查和铁路技术作业，如需换轨，出口节点需提前更换牵引机车，而换装作业则是在进口过境点完成，故进口过境比出口过境时间多一天左右。2000年，欧洲经济委员会(ECE)建议国际列车的过境时间为60 min，联运列车30 min，而实际由于各国过境政策、通关手续、铁路技术标准和能力等不一致导致过境时间差别较大。亚洲开发银行(ADB)发布的走廊性能测量和监测(CPMM)数据显示特定铁路过境点时间可能高达6 h(土乌间的阿拉特法拉普)至65 h以上(中乌间的多斯特克)[7]。

多项研究[4,7]表明，边境延误主要是因为轨距不同导致的物理换装障碍，冗杂的通关手续和基础设施导致的过境处理能力不足。边境节点延误时间呈现以下特征：

(1)边境节点发生较长时间延误的概率较低，具有明显的厚尾(Fat-tail)特征。

(2)非换装边境国家间通常签订有快速通关协议，延误发生概率较小，即fi(t|t∈(0,0+δ))较大，(0,0+δ)为t=0的右邻域。即使发生延误也能快速恢复，延误时间相对较短。

(3)边境换装站需进行大量换装技术作业和详细的通关查验，更易发生延误，且延误时间较长。

(4)同等基础设施水平和作业能力下，与作业量较少的换装站相比，繁忙的换装站发生延误的概率更高，平均延误时间也更长。若应急处理能力强，通常可在24 h 内结束延误，否则严重拥堵时列车延误可持续1周以上。

基于以上特征，假设边境节点延误时间服从两参数威布尔(Weibull)分布。其密度函数、分布函数和数学期望分别为

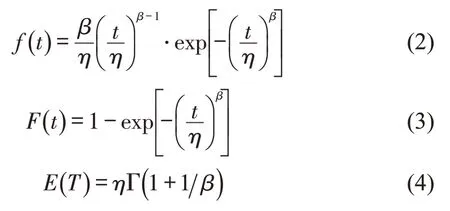
式中：β为形状参数(Shape Parameter)；η为比例参数(Scale Parameter)，t≥0,β>0且η>0；Γ 为伽马(Gamma)函数，

Weibull分布于1937年由Waloddi Weibull教授提出，广泛应用于工程领域的寿命、失效和可靠性分析[8]。其不仅具有厚尾特性，还能通过灵活的参数取值准确刻画不同类型边境节点的延误时间分布特征。0<β≤1 时，概率密度初期较大且随t快速下降，可用于描述非换装站的延误特征；β>1时，概率密度初期较小且随t先增后减，结合比例参数η可调整概率密度函数的峰值大小和对应的时间尺度，可用于刻画不同繁忙程度和应急处置能力下的换装站延误时间分布特征。图1为Weibull分布概率密度及分布函数示意图。

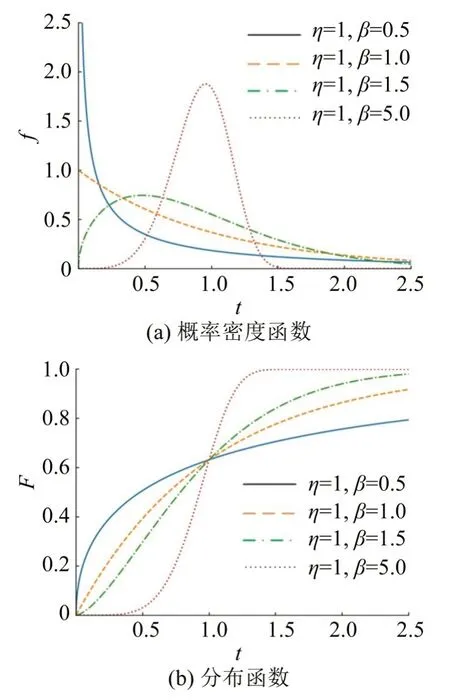
图1 Weibull分布密度函数和分布函数Fig.1 Density function and cumulative probability distribution of Weibull

1.2 单位时间延误损失

根据货物价值理论，货物k的单位时间价值损失csun,k包括货物折损价值csun,k,v和延误期货物资金用于周转产生的效益csun,k,t。假设Wk为货物k的单箱市场价格，α为资金社会折现率，μk为月贬值率，hk(t)为货损价值函数，φ为修正系数，则节点i由于时间延误造成货物k的单箱单位时间损失为

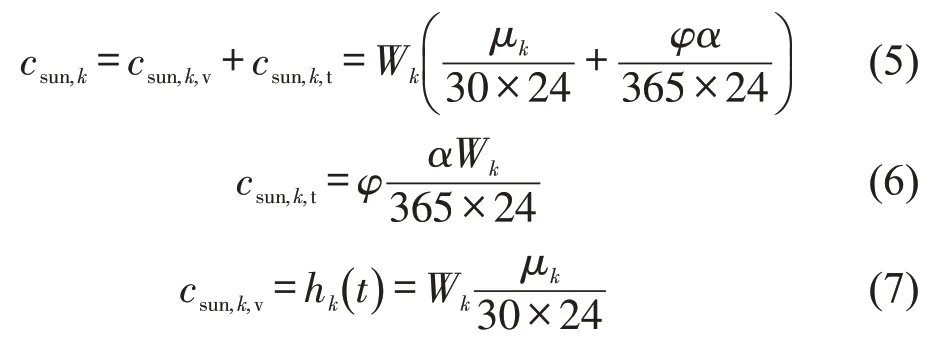
综上，边境节点i的延误风险值为

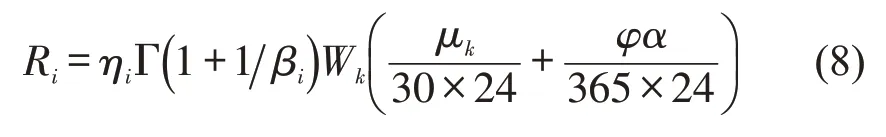
式中，ηi为节点i的延误时间分布的比例参数；βi为其形状参数。

2 中欧班列运输路径选择模型构建

铁路合作组织(OSJD)规定跨境运输货物规格的变更和相应的转运需求由“进口国”处理，因此同一站点班列去程和回程发生延误的概率不同。本文只考虑延误风险更大的进口过境延误，将边境站抽象为距离为零的虚拟边连接的相邻节点，构建网络。

G=(V,E)为中欧班列运输网络，V为节点集合，E为边集合。i,j表示班列始发站、途径的边境站、枢纽站和终到站，i,j∈V。沿线国家集合S={sg|g=1,2,3,…,n}，sg为第g个国家，n为国家个数。每个国家内部的节点集为，当i∈Vsg，节点i在sg国内部。同一国家内部弧的集合为，两国边境站间虚拟弧的集合为E′。对于弧e=(i,j)，当e∈，记为；当e ∈E′，记为，sg′为与sg相邻的国家。

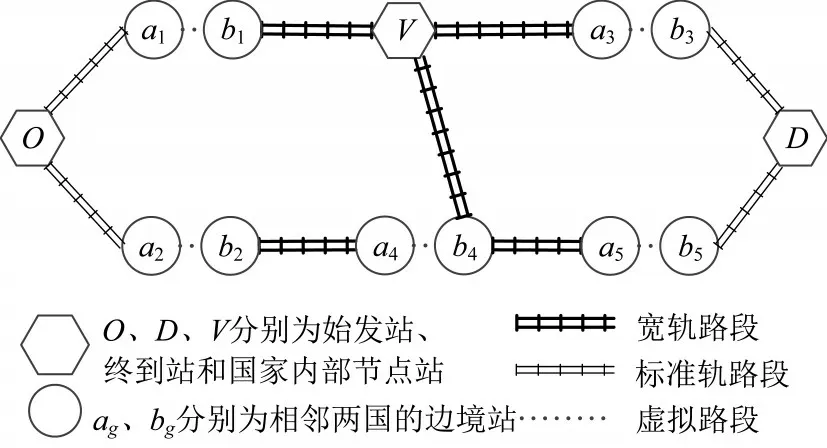
图2 中欧班列运输网络示意图Fig.2 Sketch map of transport Network of CRE

中欧班列运输网络各项参数设定如下：

l(e)——节点i到j的运价里程(km)，，其中，为sg国内节点i到j的运价里程；

t(e)——节点i到j的平均运输时间(h)，，其中，为sg国内节点i到j的平均旅行速度，为边境站停留时间，由边境站换装时间和通关时间构成，即

c(e)——节点i到j的单位运输费用(美元·箱-1)，，其中，为sg国内节点i到j的运价率(美元·箱公里-1)，为边境站作业费用，由边境站换装作业费用和固定作业费用构成，即

——中欧班列从国家sg的边境节点i到国家sg′的边境节点j的延误风险，由第1 节可知，

xij——中欧班列路径选择的决策变量，

(1)目标函数

以中欧班列路径选择经济、高效和安全为目标，考虑时间成本、风险成本和运输费用，构建综合运输成本最小的路径选择模型。

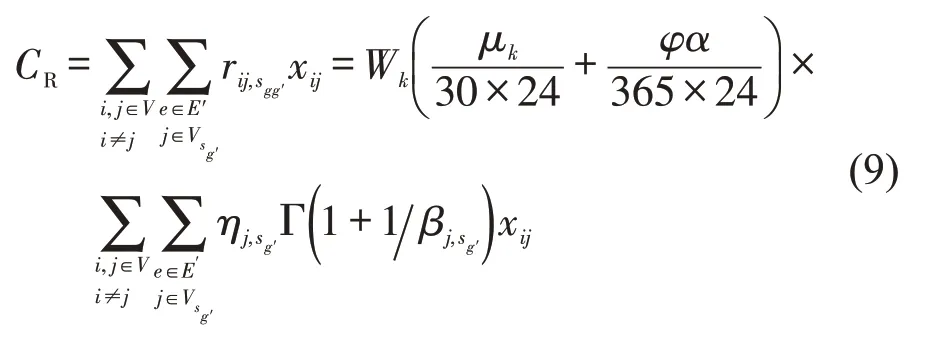
假设节点风险独立且不存在风险传递，风险成本为线路上各边境站的延误风险之和，即运输费用CC为各边境站和各路段费用的总和，时间成本CT为运输时间与单位时间货物价值损失的乘积。因此，目标函数为

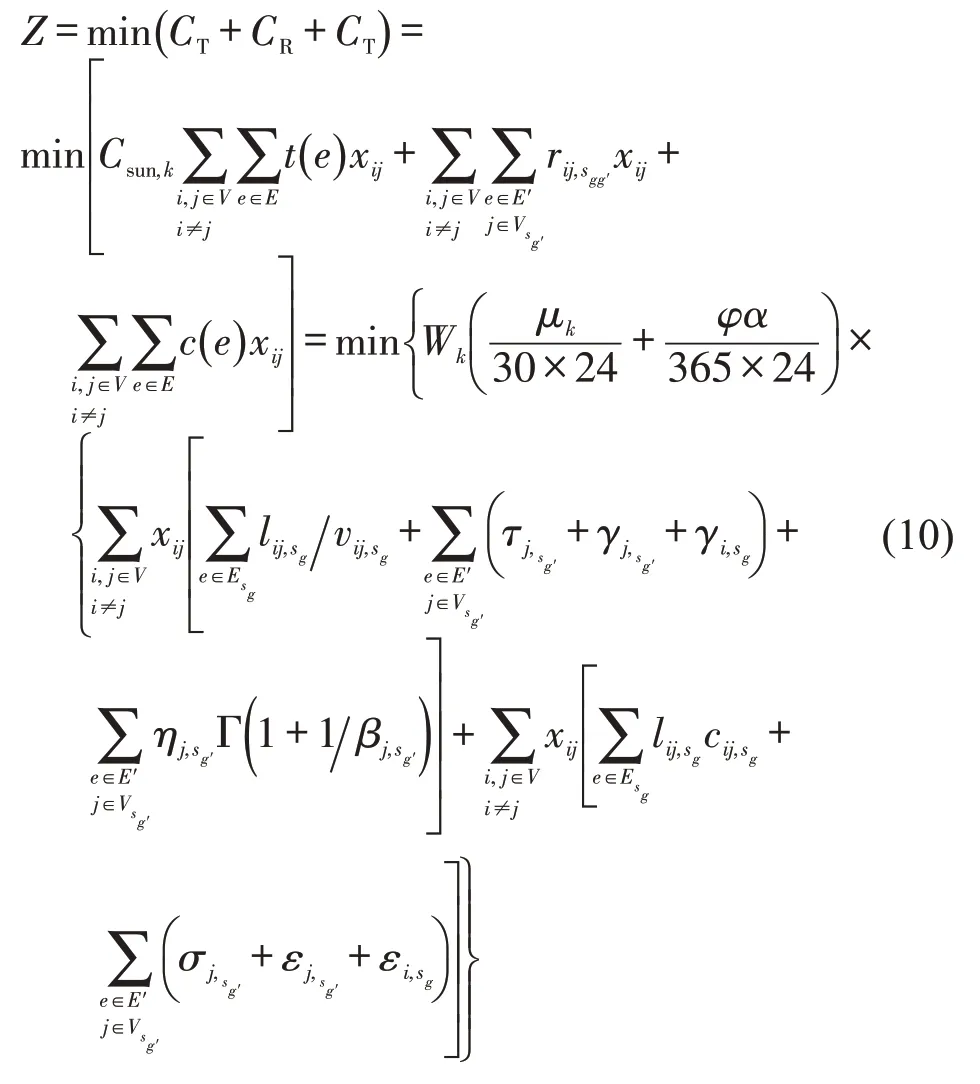
(2)约束条件

运到时限约束为

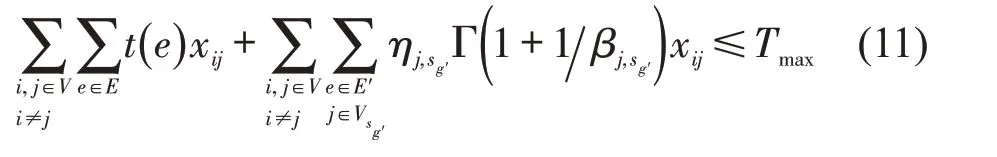
货流唯一性约束为

逻辑约束为

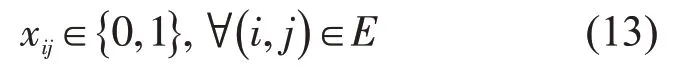
(3)路径平均风险延误率

定义路径平均风险延误率λ衡量线路m延误水平，Tm为线路m的运输时间。

3 实例分析

3.1 案例及运输网络

根据文献[4]和《中欧班列建设发展规划(2016-2020)》用ArcGIS 软件构建中欧铁路运输网络。该网络有61个节点，包括36个城市节点，25个边境节点(其中8个换装点)。以成都到柏林开行中欧班列为例进行案例研究。参数设计如下：①国内外运价率，班列运输速度，各项作业时间、费用等参考《国际铁路货物联运统一过境运价规程》(2019)和文献[2-6]，并结合成都国际班列公司调研情况确定，具体如表1和表2所示；②节点间铁路运距通过ArcGIS导出；③运到时限Tmax=25 d。

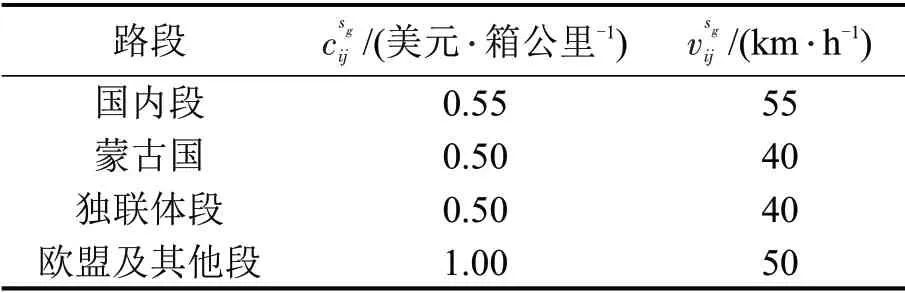
表1 路段固定参数Table 1 Value of parameters of rail

表2 边境节点参数Table 2 Value of parameters of borders

3.2 货物价值及边境延误

选择4 种价值特性的货物分析其对路径决策的影响。参考海关统计数据和文献[2，6]，以40 ft箱为参考标准，设置货物参数如表3所示。资金社会折现率α取4.5%，φ取1/16。

表3 各类货物参数设置Table 3 Parameter settings of 4 kinds of cargo

将25 个边境站分为非换装站，不繁忙换装站和繁忙换装站3 类，根据边境站延误时间特征对3类节点的延误时间分布进行仿真，参数如表4所示，概率分布如图3所示。

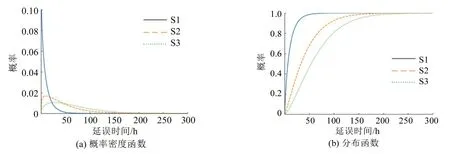
图3 3种边境站延误时间概率分布Fig.3 Probability distribution of delay time for 3 types of borders

表4 3类边境站延误时间分布参数Table 4 Parameter values of 3 kinds of borders

3.3 案例求解

(1)边境延误风险计算

仿真结果显示，非换装站延误均值为10.5 h，换装站延误均值约2 d，繁忙节点延误较多。单箱货物延误风险价值表明，不同品类货物延误成本受货物本身价值影响明显，受货物贬值影响较小，高价值货物对延误风险的敏感性强。

(2)各运输径路风险分析

中欧班列从中国运行至欧洲至少要经过两次换装，换装节点地理位置制约着线路的走向，据此将中欧运输线路划分为7类，采用深度优先遍历算法求解各类线路方案下最短路径的时间、费用和延误风险情况，表5为高价值货物K1的计算结果。

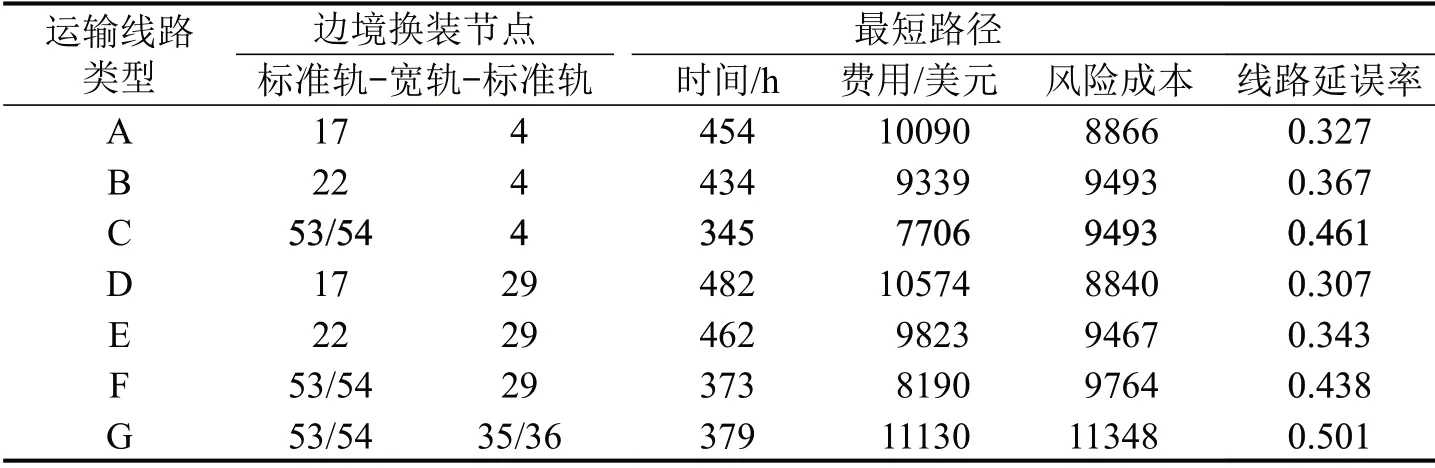
表5 各运输线路最短路径比较Table 5 Comparison of the shortest paths of different routes

C为最优路径，从满洲里或二连浩特出境至马拉的线路A和B的路径平均风险延误率都小于线路C，但时间和费用成本均过高更适合运输低价值货物。经伊朗、土耳其的线路G在费用和风险上竞争力较小，但在黑海和里海开展铁海联运可缩短运距，降低运输成本。经乔普/扎洪换装的线路D、E路径平均风险延误率较小，线路F 运输时间较短，是次优路径。乌克兰乔普站地理位置优越，是独联体宽轨路网到中南欧的终点，但目前能力不足，乌克兰也正努力改善基础设施及货运状况，未来该换装站可能成为中欧班列进入欧洲的又一重要门户，极大缓解马拉口岸的货运压力。

(3)最优路径选择

4 种品类货物最优路径方案相同，结果如表6所示。全程约14 d，单箱运费约7706 美元，路径平均延误率为0.46，即该线路总边境延误时间期望接近运输时间的50%。结果与联合国欧洲经济委员会(ESCAP)基于2017年亚欧运输线路数据的报告一致[7]。高价值货物如K1的边境延误成本是运费的1.2 倍，占总成本25%，而低价值货物如K4的延误成本和时间成本之和只占总成本的0.7%。对此运营企业和相关部门应予以重视，在口岸能力不足时，优先安排高价值货物通过可在一定程度上降低承运人损失。

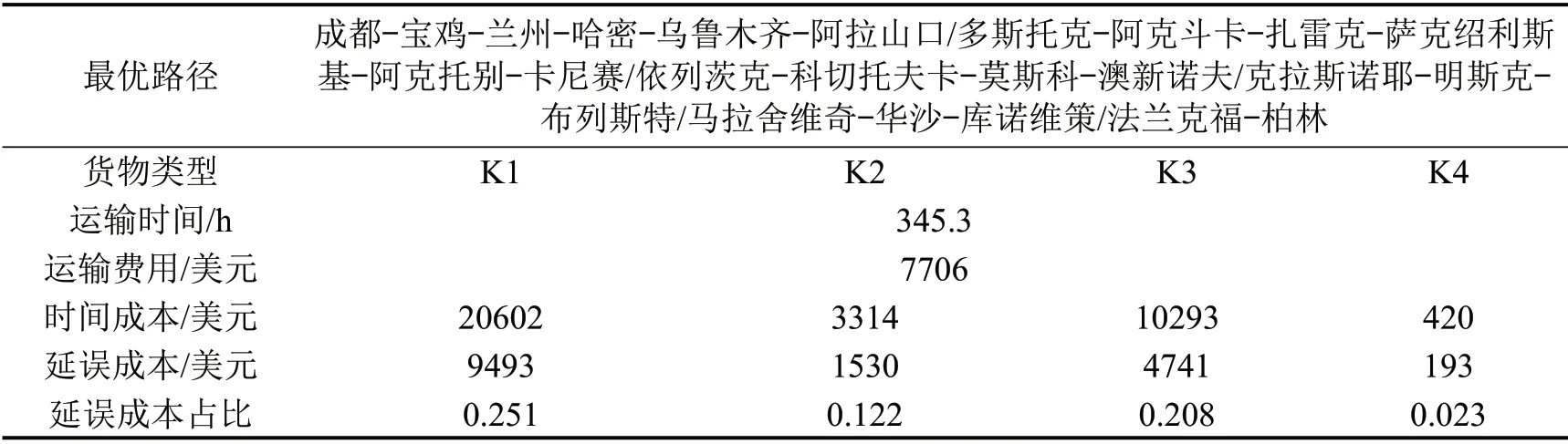
表6 最优路径方案Table 6 Details of optimal route

近年来，中欧铁路合作不断提升，在各方积极努力下大部分中欧班列延误可控制在1 周以内。但在全球疫情冲击下，班列开行数量不断增加，境外口岸接车能力及应急处置能力的不足严重影响班列时效。2020年国铁集团多次发布出境口岸停装或除中欧班列以外出境货物停装命令以应对境外口岸拥堵。因此，相关部门应加强对沿线边境节点延误信息的掌握，建立中欧班列口岸突发事件及拥堵预警机制。运输企业则要重视边境延误风险，提高风险应急处理能力，在全球疫情影响下抓住机遇提高中欧班列市场竞争力。

4 结论

本文通过分析边境站点时间延误特征，提出延误风险测算方法并建立综合成本最小的中欧班列路径选择模型，主要结论如下：

(1)边境换装站平均延误约为2 d，线路边境延误时间均值为5～7 d，边境节点延误严重影响中欧班列运输时效和服务水平的提高。

(2)单位集装箱货物价值越高，延误造成的风险成本越大。高价值高贬值率货物对运输路径的安全需求及运输服务水平要求更高。

(3)由于中欧线路运输距离长，时间和费用成本仍是决定线路选择的重要因素。阿拉山口到马拉仍是目前中欧班列最优路径，但其线路边境延误时间均值接近运输时间的50%，加强对马拉口岸能力信息的掌握和延误时间的预判在短期内有助于提高班列服务水平。