节点中断与需求不确定下的港口供应链整合

赵旭，张汇妍，黄瑞

(大连海事大学，交通运输工程学院，辽宁大连116026)

0 引言

近年来，为提升链条的运作效率和营运收益，位于港口供应链核心地位的港口企业选择整合资源，与上下游企业节点进行系统合作。然而，链条上节点数量增多以及全球突发事件的发生，使得链条整合面临各种不确定性。针对链条的物流服务功能，考虑企业节点中断和货运需求的不确定性，如何选择链条整合策略是值得探讨的问题。

在港口供应链整合研究方面，Han C.H.等[1]运用因子分析与回归方法，探讨釜山集装箱案例中，港口供应链整合对港口绩效的影响；Mira M.S.等[2]采用偏向结构方程方法研究人力资源管理和港口绩效对港口供应链整合的作用。在不确定性分析方面，燕晨屹等[3]主要考虑需求和运输成本不确定情景，建立供应链网络海外仓的选址模型；Thekdi S.A.等[4]重点研究各种中断情景突然发生对港口供应链经济活动的影响，并提出对应的保护措施；Yu Y.等[5]将供应链整合和组织风险引入降低供应链风险的模型中，验证供应链风险与供应链整合负相关；Ha M.H.等[6]结合证据推理与层次分析法研究韩国港口供应链系统，判断各种风险因素对于整合的影响。

目前，港口供应链整合问题的研究对象大多为单一港口，分析不确定环境下多港口协调引导链条整合的研究成果较少。在此基础上，本文设计不同决策者对于中断和需求风险的置信水平，对比分析各层级节点与多个港口之间的合作关系，建立双层规划模型使整个系统的整合收益最大化。

1 问题描述与建模

1.1 问题描述

港口供应链通常为多条以服务供应商、港口和客户为节点的三级供应链结构[7]。本文针对链条中基本的物流服务，建立对应的三级结构，如图1所示。物流服务供应商，包含进出口车队和船公司；核心企业，包含起始港和目的港；物流服务需求方，包含货主和目的地。

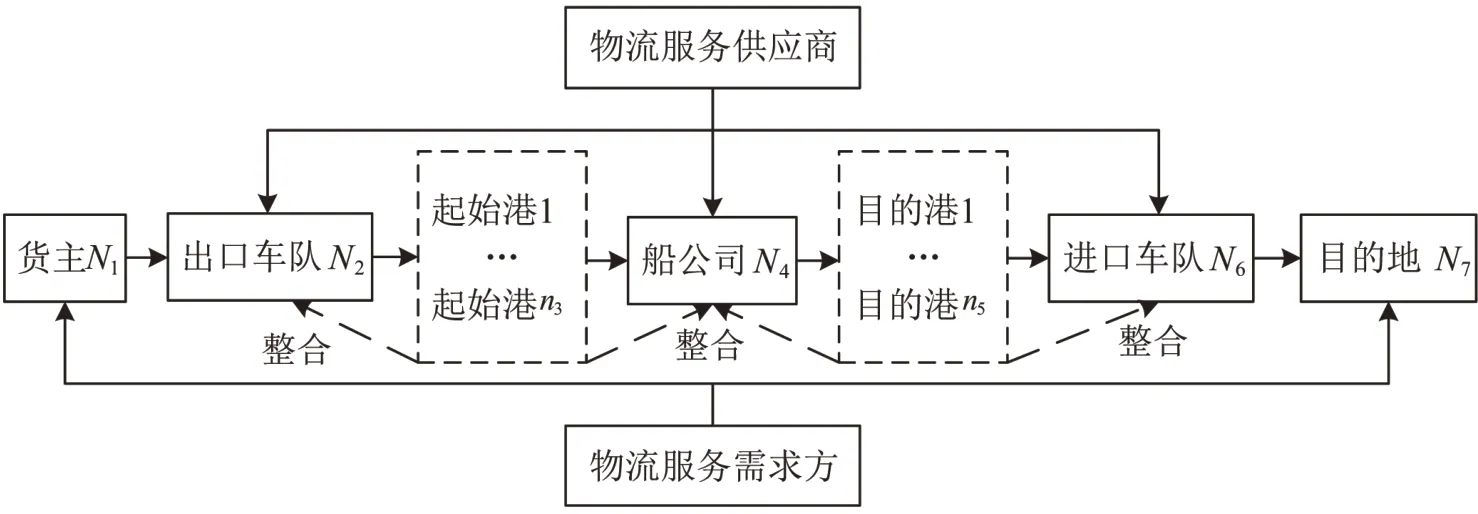
图1 港口供应链构建Fig.1 Port supply chain design

1.2 模型假设

港口供应链物流资源整合是一个复杂的问题，为便于建立数学模型，故对模型做出以下假设：

(1)该港口供应链重点关注物流服务及物流服务供应商，暂不对其他种类的服务及服务供应商做分析；

(2)港口供应链整合后的利益分配服从利益共享契约，即港口将一部分收益交付其整合的物流服务供应商；

(3)物流服务供应商参与整合后会降低对物流服务需求方的收费，以增加经过该港口和供应商之间的货量；

(4)各物流服务供应商若选择参与整合，则仅选择参与一个港口主导的整合，出口车队只参与起始港整合，进口车队只参与目的港整合，船公司既可以参与起始港整合也可以参与目的港整合。

由于无法描绘港口供应链中的所有不确定情景，本文仅考虑节点中断和需求不确定情景对链条的影响，忽略其余不确定性的作用。另外，对于节点中断情景做出如下假设：

(1)物流服务需求方不发生中断；

(2)若节点发生中断，货物不能流经该节点，物流服务需求方将默认选择其他节点连续路径运输，暂不分析中断时间的影响；

(3)本文引入缺货成本，表示由于物流服务供应商的大规模瘫痪，无法完成物流需求的惩罚成本，实际缺货成本由多方因素影响，不是单位缺货成本的简单线性函数，但本文暂不做细化分析，将单位缺货成本设置为8000美元·TEU-1。

1.3 模型参数

模型中的输入变量和决策变量如表1所示。

表1 模型参数Table 1 Model parameter

1.4 双层规划模型构建

从港口供应链整体收益和物流服务需求方总成本两个角度考虑，分别建立上层收益最大，下层成本最小的双层规划模型。

(1)上层规划

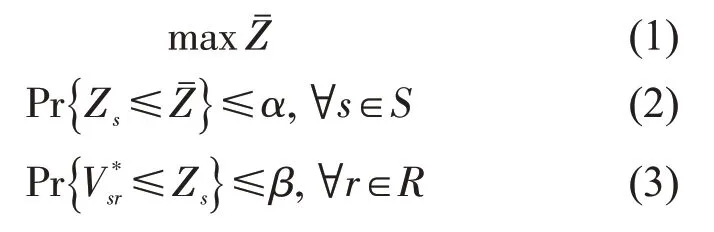
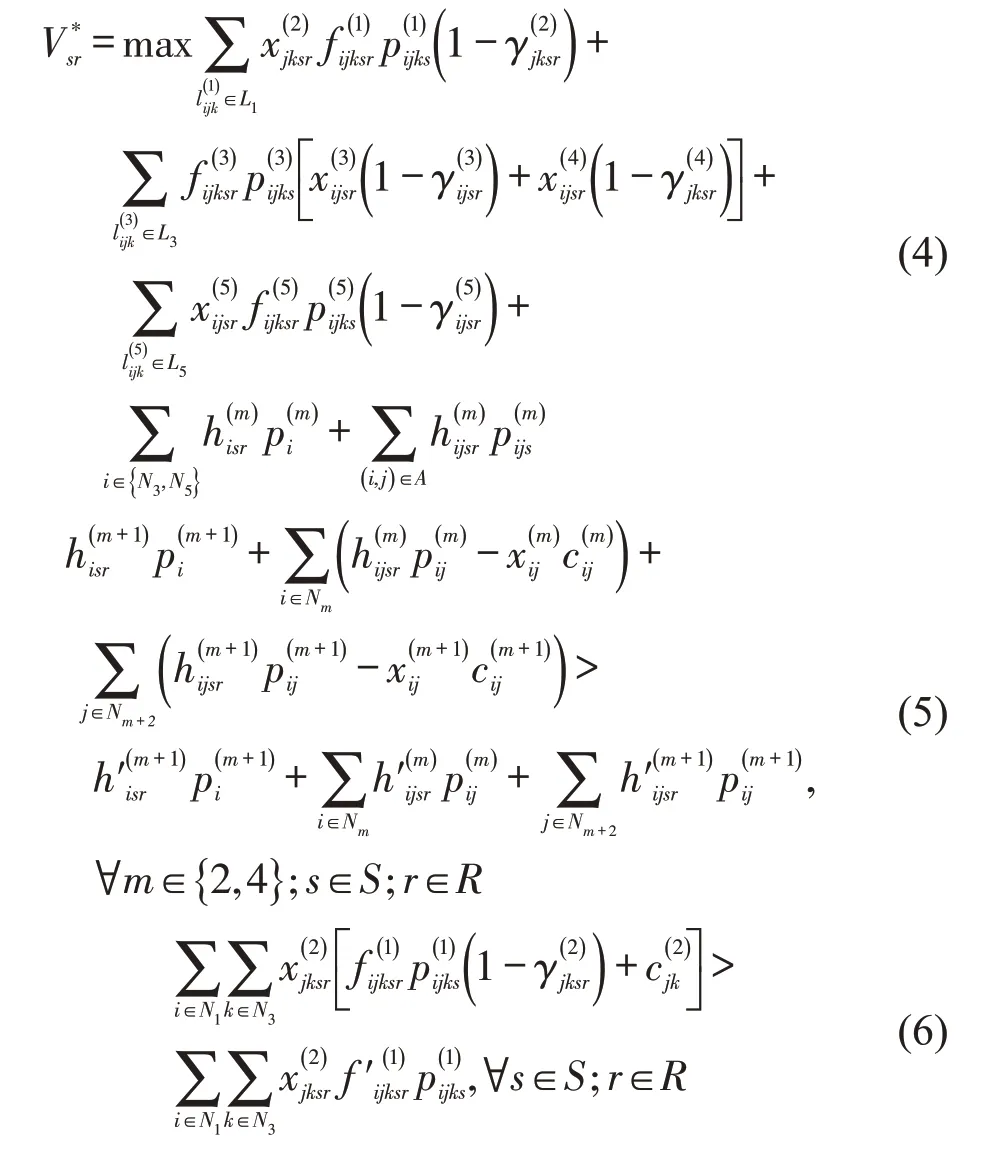
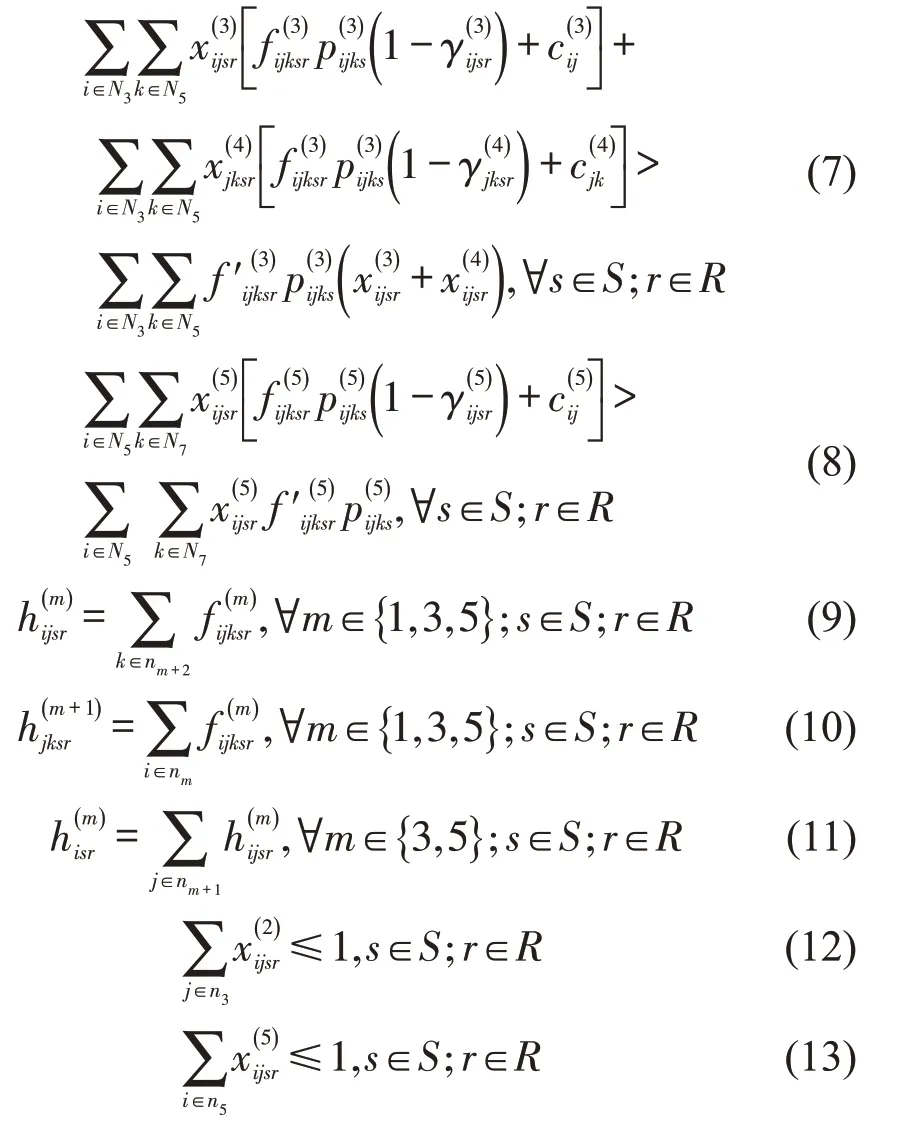
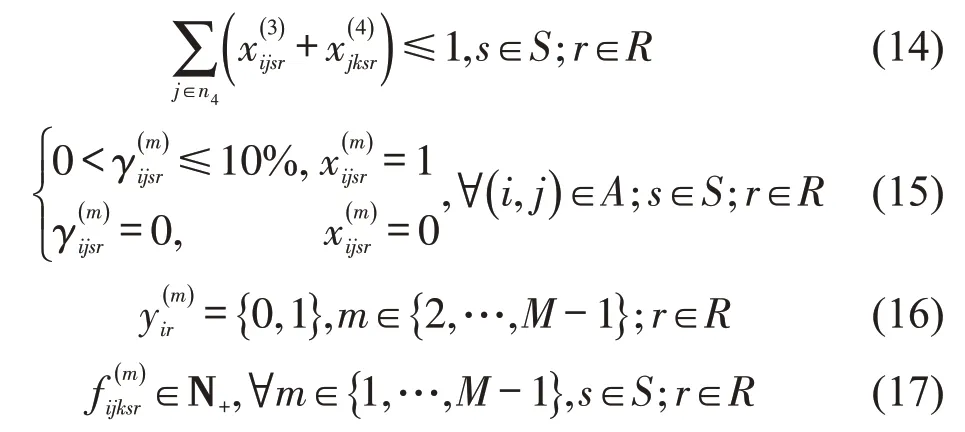
式(1)为最大化两种不确定风险下的港口供应链整体收益；式(2)要求每一需求情景下的总收益不超过----TZ的比例不能超过α；式(3)要求在某一特定需求情景下，每一节点中断情景的总收益不超过TZs的比例不能超过β；式(4)表示需求和节点中断下合作后港口供应链的整体收益；式(5)～式(8)分别表示港口、出口车队、船公司、进口车队整合后收益应大于整合前收益；式(9)和式(10)表示港口供应链节点间的货量；式(11)表示流经起始港节点和目的港节点的总货量；式(12)表示出口车队只参与起始港的整合；式(13)表示进口车队只参与目的港的整合；式(14)表示船公司只参与起始港和目的港中的一个港口引导的整合；式(15)表示折扣系数只有整合时大于0；式(16)～式(17)表示0-1 变量和正整数约束。

(2)下层规划

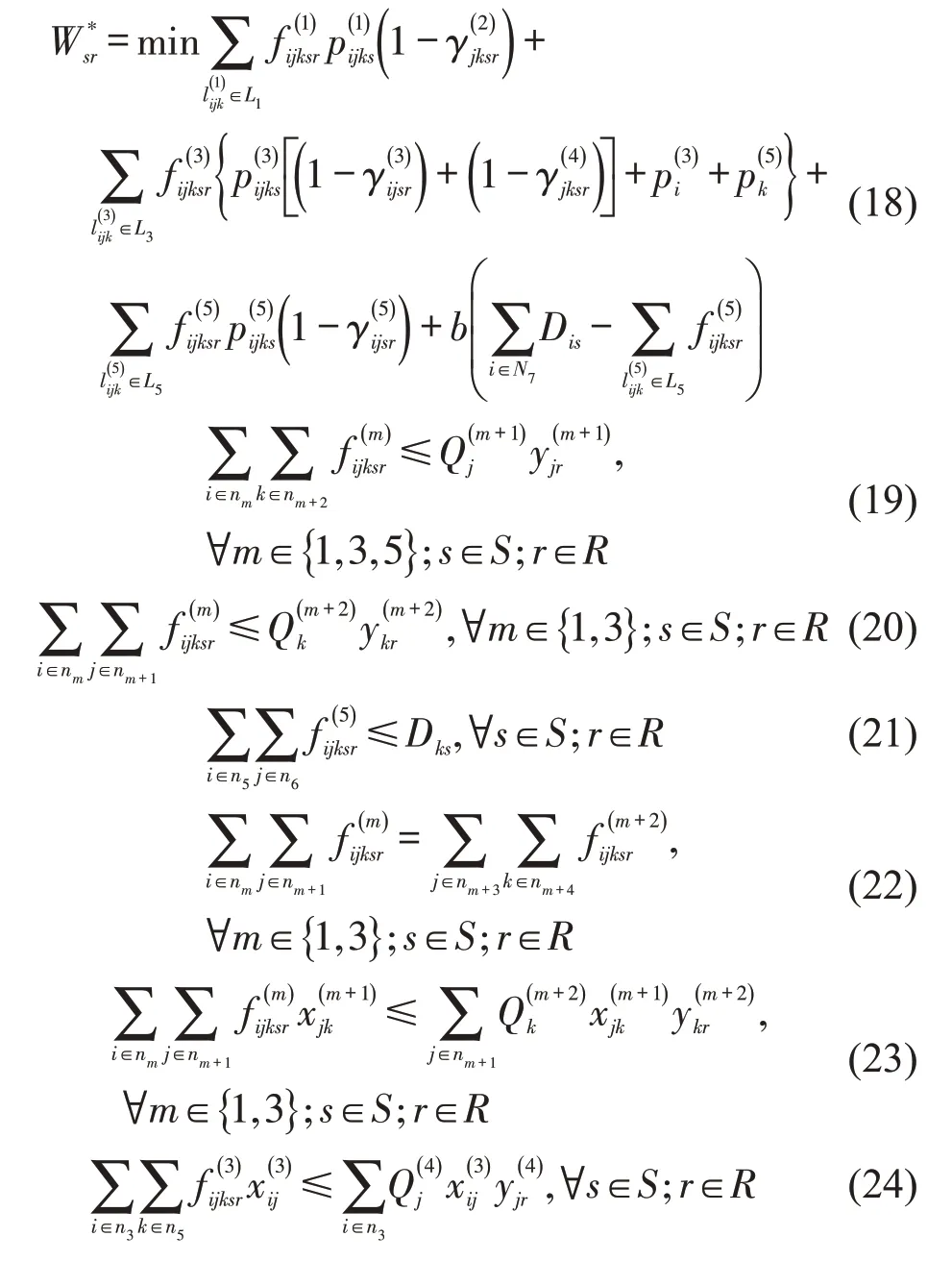
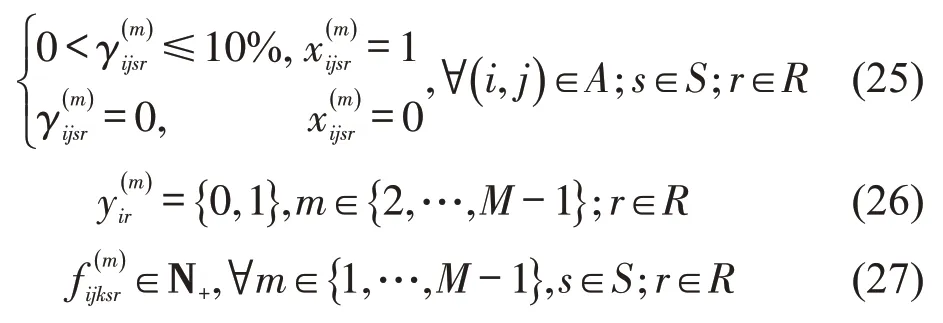
式(18)为在中断情景和需求情景下最小化物流服务需求方的成本，包括运输成本、港口作业成本、中断缺货成本；式(19)～式(20)要求若没有发生中断，子链上的货量不能超过节点的服务能力；式(21)表示流入目的地的货量不能超过需求情景下的目的地需求；式(22)表示子链上各节点间货量流入等于流出；式(23)～式(24)表示若没有发生中断，物流服务供应商整合后货量不超过港口节点的容量限制；式(25)表示折扣系数只有整合时大于0；式(26)～式(27)表示0-1变量和正整数约束。

2 模型求解

根据不确定双层规划模型，设计结合随机模拟、最短增广链算法、遗传算法的混合遗传算法，如图2所示，图中，gmax为最大迭代次数。上层规划中使用随机机会约束规划的求解算法，下层规划中嵌入最短增广链改进算法。

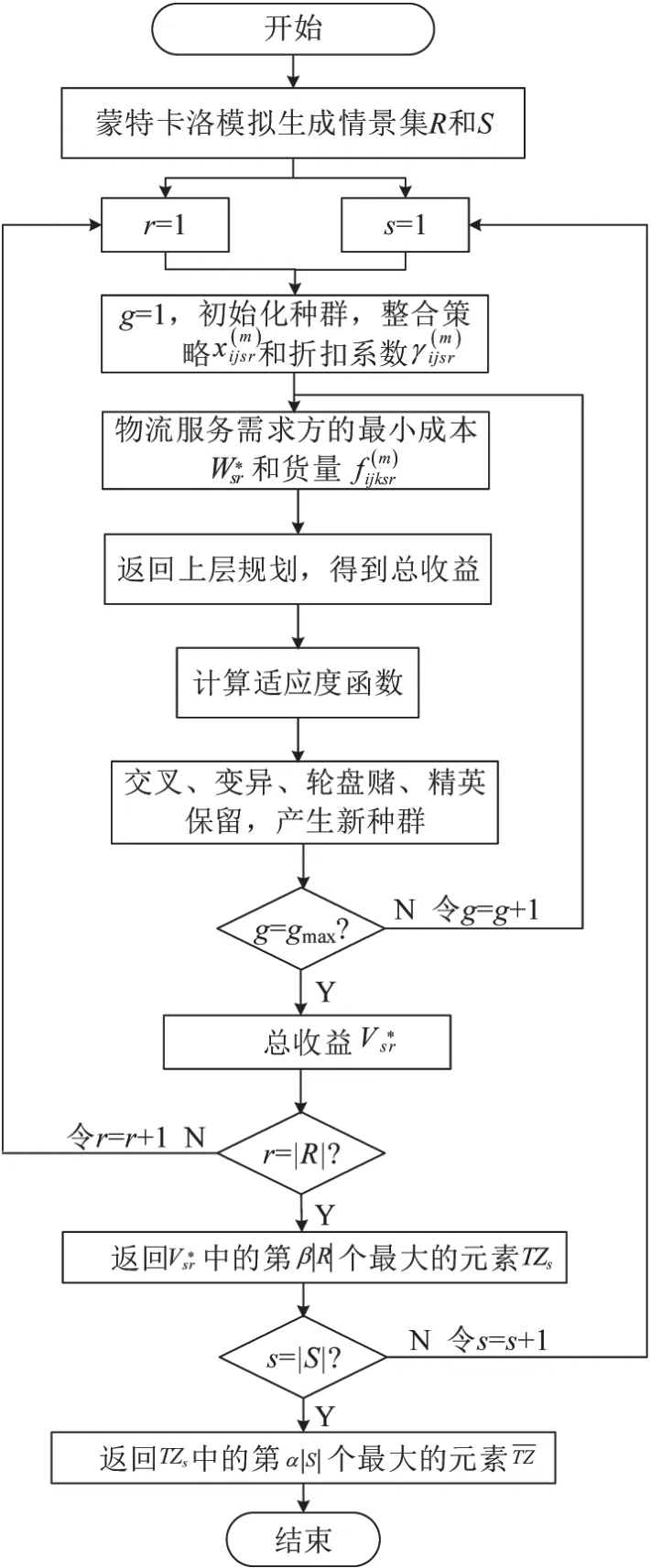
图2 混合遗传算法流程图Fig.2 Flow chart of hybrid genetic algorithm

(1)随机机会约束规划

上层规划本质上是随机机会约束规划，包含两个随机变量，分别是中断情景r和需求情景s。其中与随机变量有关的式(2)和式(3)可以转化为Maximax模型中乐观值模型，模型具体定义可参考亓尧等[8]的文献。对于此类规划，通常采用随机模拟和遗传算法相结合的求解算法。

(2)最短增广链改进算法

下层规划可以转化为具有容量限制的经典最小费用流问题。在传统问题中，两个节点之间只能连接一条路径。特殊的是，在港口供应链中，每段子链的收费是由连续的3 层节点的连接路径决定的。因此，在构建网络时，两个节点之间需要连接多条路径。例如，货主1 与起始港1 之间连接多条路径即出口车队，这样路径上能记录3个层级的节点。为提高程序运行速度，借鉴邵丽萍等[9]提出的最短增广链改进算法，得到最小费用子链后，在分层剩余网络中寻找下一条最小费用子链，避免网络节点的反复遍历。

3 案例分析

以远东-欧洲航线为研究对象，构建港口供应链，包含6个货主、7个出口车队、2个起始港、5个船公司、2 个目的港、7 个进口车队和3 个目的地。决策者需给出对需求不确定风险和节点中断风险的置信水平，决策所有起始港和目的港引导的港口供应链整合策略，使得整合后整体收益最大，物流服务需求方成本最小。

3.1 案例数据

根据克拉克森数据库报告，整理分析得到，新冠疫情背景下2020年远东-欧洲航线的货运量和运价的变化趋势，模拟4 组需求情景和5 组节点中断情景。每组需求情景出现的概率均为0.25，不同需求情景下有不同的子链价格区间，并且在区间中随机生成。另外中断情景中，设置中断节点数为1、2、3、4、7，中断节点在满足中断节点数的要求下随机生成。按照第2节算法设计，设置算法中的一些重要参数为：种群数量为10，最大迭代次数为50，精英比例为0.2，参与轮盘赌的比例为0.2。

3.2 模型结果与分析

若不考虑决策者对风险的置信水平，选取5组不同的节点中断和需求不确定风险情景，求解整合前后的收益，结果如图3所示。发现：在面对真正的风险情景时，整合的港口供应链获得总收益的能力要优于不整合时的港口供应链，但在风险情景3中，这种能力并不是很突出，说明整合只能在一定程度上提升这种能力。

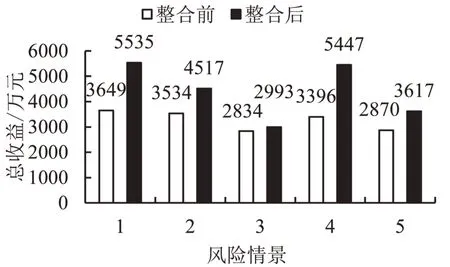
图3 风险情景下整合前后收益结果Fig.3 Results of income before and after integration under risk scenarios

设置不同的风险置信水平组合对比分析，由于最近全球疫情影响，决策者对于风险发生的判断通常是悲观的，认为这两种风险都极有可能发生。因此，将α和β的范围缩小，0.5≤α≤1，0.5≤β≤1。本文设置α和β为α=0.6,0.8，β=0.6,0.8。在疫情没有发生时，决策者通常对节点中断置信水平乐观，需求风险悲观，为了对比，另外设置一组β=0.2。

根据建立的双层规划模型，通过Matlab程序计算得出合作策略和收益结果如表4所示。为便于描述结果，起始港对应的是进口车队(1～7)和船公司(1～5)，目的港对应的是出口车队(1～7)和船公司(1～5)，以“[]”区分车队和船公司。

从本案例来看，同一置信水平下每个港口整合的节点数量与具体节点都不相同，在一定程度上反映从多港口的角度考虑是具有实际意义的。表2中，对比疫情前后的两组置信水平设置，发现不仅疫情后的总收益有所下降，整合策略也有一定程度上的调整。另外，观察不同置信水平组合，同一港口的整合策略有很大区别；在α增加，β不变时，总收益大约减少1000万元；类似地，β的增加也会带来收益减少的影响，但是相比于α，数值降幅更为明显，说明节点中断置信水平对链条整合收益产生影响更大。因此，港口在引导整合时，除物流需求变化外，也应进一步保护链条节点的连续性，防止其发生中断。

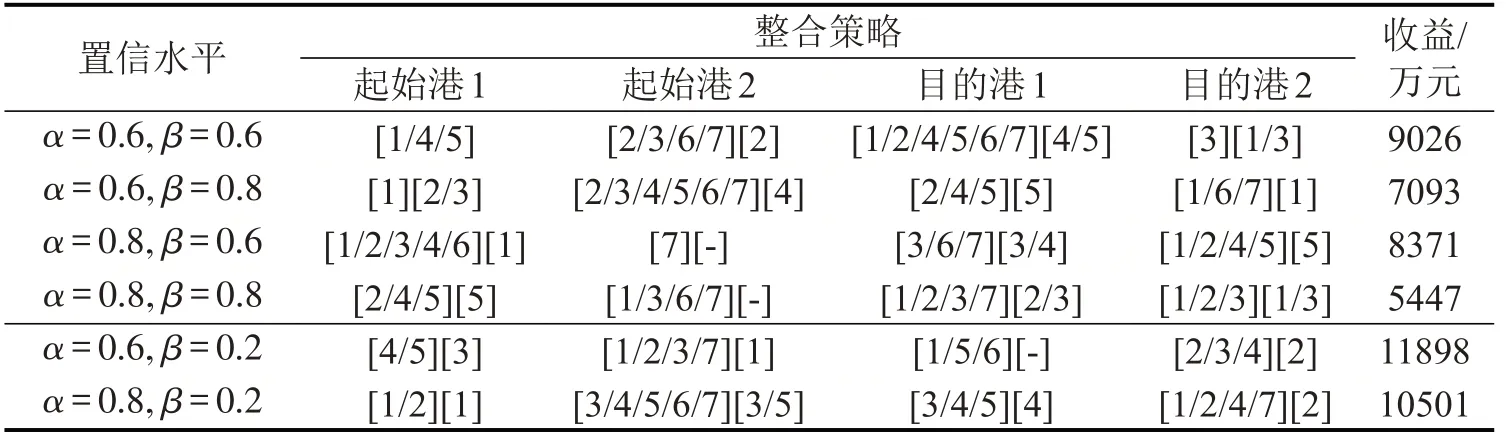
表2 不同风险置信水平下的整合结果Table 2 Integration results under different risk confidence levels

4 结论

在节点中断和需求波动的不确定环境下，构建不确定双层规划模型，并设计混合遗传算法进行求解，得到港口供应链的整体最优收益和多港口整合物流服务供应商的最优策略。由案例结果可知，不同风险置信水平下，链条上所有港口的整合策略会发生改变，进而影响链条的总收益，其中节点中断风险对港口供应链的影响更为突出；进一步结合具体风险情景分析发现，当企业参与整合时，可以在一定程度上减少风险带来的损失。得到的结论与经验或事实相符，构建的模型和算法具有可行性，可以为研究不确定条件下的多港口整合提供参考。