特征结构配置法在无人机控制系统中的应用研究*
于海生,吕 卉,龙飞虎,董义兵
(尚良仲毅(沈阳)高新科技有限公司/辽宁省产业技术研究院无人机研究所,辽宁 沈阳110000)
从本质上来说在过去的很长一段时间内使用极点配置控制系统属于线性系统一种,线性系统的时域性特征能够根据指标要求转化为期望极点,然后通过定位期望极点实现状态反馈、输出反馈、极点配置等。这种逻辑思路存在明显的局限性,当使用不同的方法求解时极点可能处于不同的状态增益,简单来说极点配置的运行逻辑不具有唯一性,很容易受到其他因素干扰而出现偏差。
特征结构则是一种以闭环系统的极点为核心的控制逻辑,可以同时配置重数和特征向量,从而将极点的方向、距离信息固定化,这种控制逻辑稳定性更强,当选取参数恰当时,则可以达到期望性能状态下的控制。
本文对特征结构配置法的无人机飞控系统控制律进行了探讨,对该飞控系统中的极点和特征向量配置进行探究,分析该系统模态的解耦。
1 特征结构配置法概念
特征结构配置的起源较早,早在中世纪就有科学家提出了特征结构配置的概念,在后续的物理研究中特征结构配置法大放异彩。瑞利爵士在对振动弦和声音在空气中的传播路径的动力学特征进行研究时,以拉格朗日和哈密尔顿原理为基础总结了一种处理空气动力系统中各种模态和频率的工具,其是一种广义坐标概念,就是将振动系统响应都解析呈一系列振型和频率,从而得到一种可以描述空气动力学特征的线性时变可控和可观系统,在结合相关物理学一般规律和数学理论,其得到了一个状态方程,即:X=aX+bU和y=cX+dU,这就是特征结构配置法的最初形态,也是特征结构配置法的核心方程。
2 无人机飞控的特征结构配置
2.1 特征结构配置分析
无人机飞控特征结构配置的线性系统状态方程可表示为:
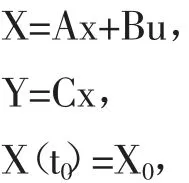
其中A是无人机飞控系统的状态阵,其反馈的是飞控系统固有的运动特性;B是无人机飞控系统的控制阵,其反馈的是输入量对飞控系统运动状态的影响特征;C是无人机飞控系统的输出阵,其反馈的是输入量进入系统后会以怎样的状态输出;x是系统的运行状态向量,u为系统的输入向量,y为系统的输出向量,X0为系统的初始值,t0为系统的初始时间。当B为0时,此时无人机将处于t0时刻的状态,其飞行状态将维持初始值不变,正常状态下可求得上述系统的解为X(t)=eAtx0,如果使用A的特征向量和特征值来表示上述飞控系统的状态方程,那么可得AV=Vλ(注:V=[V1……V2……Vn],λ=[λ1……λ2……λn]),对该状态方程可做以下解读:V表示特征向量,其是状态空间的集合,包含所有系统特征向量线性组合的集合,在特征结构配置的无人机飞控系统中可将其统称为右特征向量。与之相对的还存在左特征向量,使用W表示左特征向量,W的特点、特征、现实意义与V一致,只是在方向上相反,同时满足AW=Wλ(注:W=[W1……W2……Wn],λ=[λ1……λ2……λn])。
特征结构配置法下的无人机飞控系统的时域相应方程可以表示为以下形式:
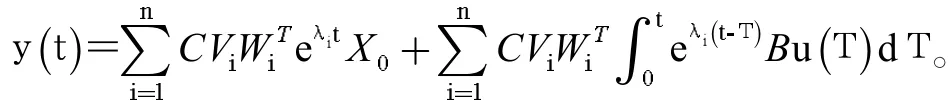
上述的方程提示了特征结构配置法下无人机飞控系统的自由响应实现路径,也明确了三个关键量,即响应相关速率的特征值、响应形状的特征向量、自由响应的初始状态。这个方程描述了输入值进入到系统后,特征值的响应特征,包含了特征向量和外作用输入影响状态的过渡过程,简单来说就是提示了时域相应对无人机运动模态的外作用输出。
2.2 输出反馈特征结构配置
特征结构配置法下的无人机飞控系统所塑造的期望是一种闭环特征,当输入一个特征值λ时,得到输出反馈。
以特征结构配置法为基础,结合实际工作逻辑,简化后可得控制律方程:u=Ly。其中K表示反馈增益矩阵,同时使用x=(A+BKC)x表示闭环方程,输入特征值λ1得到方程V1=(λ1l-A)-1BKCV1;现在假定系统的期望特征值λ和状态矩阵A的特征值并不对等,那么此时的(λ1l-A)就是一个逆存在。在特征向量假设成立的前提下,反向可解V1=N1z1。特征向量V1必须位于N的列张成的子空间中,一旦期望的特征值已确定,N的分布空间便限定了闭环特征向量的选取。而期望的特征向量不属于预先规定的子空间而不能到达,此时需用最可能到达的特征向量来代替理想特征向量V。该可达向量(理想化特征向量)是在N的列张成的子空间上的投影,使所求的特征向量尽可能靠近期望的特征向量。
3 无人机纵向运动控制律逻辑
无人机的纵向运动模态可分为两个纵向短周期、一个纵向长周期,期望每个模态起主导作用的分别是攻角、俯仰角速率和俯仰角,期望特征向量为:
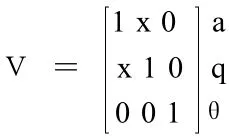
运用输出反馈特征结构配置方法得到的无人机俯仰姿态保持系统的反馈增益矩阵:K=[-0.78972.12045.3293]。
4 无人机横侧向控制律逻辑
参考纵向控制律逻辑,对特征结构配置法下无人机飞控的横向控制律逻辑进行解析,无人机横侧向运动模态可分解为滚转、螺旋、荷兰滚三种形式,其中荷兰滚有两种模态,上述运动模态以侧滑角、滚转角速率、滚转角和偏航角速率为主导,特征向量可做以下构建:
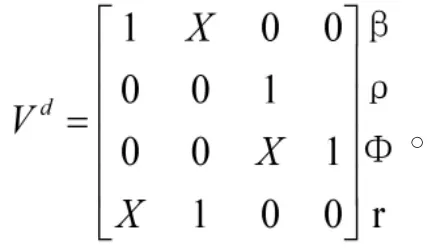
运用输出反馈特征结构配置方法得到的无人机俯横侧向姿态运动系统的反馈增益矩阵:
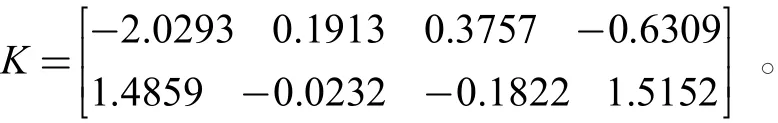
5 无人机运动飞控测试及结果
5.1 纵向运动测试
前文已经提到特征结构配置法中无人机飞控纵向运动的主导因素为攻角、俯仰角速率和俯仰角,因此从逻辑上来说从对上述三个主导因素进行调整后无人机的纵向运动模态会发生改变,下面采用仿生设计原理对变量输入后无人机运动模态变化和反馈响应情况进行总结。
首先,对俯仰角因素变化后无人机运动模态进行仿生实验和总结。利用仿生技术,输入俯仰角指令0.1754rad,仿生实验中可见无人机在1.0s内迅速做出响应,俯仰角曲率迅速上升并在短时间内曲率变化率迅速降低,直至2.0s左右完成俯仰角调整。结果提示俯仰角响应无超调,稳态无误差,无人机可在2.0s内完成俯仰角调整。
然后,对俯仰角变化过程中俯仰角变化速率进行观察和总结。利用仿生技术,输入俯仰角指令0.1754rad,仿生实验中可见无人机俯仰角速率曲线呈单峰特征,指令输入后先迅速上升再迅速下降,最后趋于平稳,俯仰角速率在0.6s达到峰值,最大速率在0.25rad/s-0.28rad/s之间,1.5s时达到既定俯仰角,此时俯仰角变化速率为0.0rad/s。仿生实验结果提示俯仰角调整信息输入后该飞控系统可在短时间内进行响应和反馈,从指令下达到达成时间可锁定在2.0s以内,提示特征结构配置法下的无人机飞控系统稳定性较强、响应速度较快。
最后,对俯仰角变化过程中无人机攻角变化特征进行观察和总结。利用仿生技术,输入俯仰角指令0.1754rad,仿生实验中可见无人机攻角变化和升降舵偏转,根据系统分析结果,指令输入后1.2s内无人机攻角0.13rad/s增加,升降舵偏转角最大增量可达0.44rad/s。整体上来看,攻角变化曲线呈单峰特征,先迅速上升再匀速降低,最后归零,使得无人机可在俯仰角变化的基础下稳定升降;升降舵偏转角偏转曲线则呈现一峰双谷特征,在指令下达后0.4s内迅速降低,在0.4s-1.1s内迅速升高至峰值,在1.1s-2.0s内迅速降低,2.0s后缓慢升高并归零。
综合来说,从上述的仿生实验及数据中心可以确定:(1)特征结构配置法下,无人机飞控系统具有较快的响应速度,从指令下达到达到既定状态不超过2.0s,响应速度较快,可满足绝大多数情况下的纵向调整需要,具备快速反应特征。(2)特征结构配置法下的无人机飞控系统响应期间系统稳定性较强,具有明确的变化特征,变化速率快、稳、准,可靠性和安全性较强。
5.2 横向运动测试
前文已经提到特征结构配置法中无人机飞控横向运动的主导因素为侧滑角、滚转角速率、滚转角和偏航角速率,因此从逻辑上来说从对上述四个主导因素进行调整后无人机的横向运动模态会发生改变,下面采用仿生设计原理对变量输入后无人机运动模态变化和反馈响应情况进行总结。
首先,对滚转角因素变化后无人机运动模态进行仿生实验和总结。利用仿生技术,输入滚转角指令0.52356rad/s,仿生实验中可见无人机滚转角迅速变化,滚转角曲率迅速上升并在短时间内曲率变化率迅速降低,1.5s内完成上升动作,2.0s内完成所有动作调节,最大增量0.51rad/s,2.0s后滚转角变化曲率归零,提示达到既定调整目标,滚转角响应无超调,稳态无误差。
然后,对滚转角变化过程中的滚转角变化速率进行分析和总结。利用仿生技术,输入滚转角指令0.52356rad/s,仿生实验中可见无人机滚转角速率曲线呈无峰特征,指令输入后1.0s内滚转角迅速上升,并于1.2s达到既定滚转角,此时滚转角变化速率为0.0rad/s。仿生实验结果提示滚转角指令输入后该飞控系统可在短时间内进行响应和反馈,从指令下达到达成时间可锁定在1.5s以内,提示特征结构配置法下的无人机飞控系统稳定性较强、响应速度较快。
对无人机俯仰角变化过程中偏航角速率进行观察和总结。利用仿生技术输入滚转角指令0.52356rad/s,仿生实验中可见无人机偏航角变化速率和偏航角变化曲线,整体上偏航角速率随着滚转角的调整而变化,曲线上呈单峰特征,0.4s内迅速上升并达到峰值,0.4s-1.5s内迅速降低,1.5s后缓慢降低最终于3.0s时归零,峰值时偏航角速率最大可达0.06rad/s,滚转角调整完成后偏航角速率降低至0.02rad/s。同时方向舵偏航角曲线则呈现匀速降低,随着滚转角调整偏航角曲线迅速降低,直至最低值。
最后,对滚转角变化过程中无人机侧滑角变化特征进行观察和总结。利用仿生技术,输入滚转指令0.52356rad/s,仿生实验中可见无人机侧滑角变化和方向舵偏转,根据系统分析结果,指令输入后1.2s内无人机侧滑角0.0085rad/s增加,滚转角达到稳定状态时,侧滑角为-0.003rad,协调转弯过程中侧滑角实现了零保持。副翼偏转角最大增量约0.16rad,稳态值约O.0025rad。方向舵偏转角最大增量约0.11rad,稳态值约0.008rad。
综合来说,从上述的仿生实验及数据中心可以确定:(1)特征结构配置法下,无人机横向控制响应速度较快,最快响应时间在1.5s以内。(2)特征结构配置法下的无人机横向控制反馈结果可靠,协调转向零保持,稳定性极佳。
6 结束语
本文对无人机特征结构配置法飞控系统下的模态方程和控制律进行分析,同时结合仿生实验对该系统的输出反馈情况进行探究,实现了该飞控系统内部的解耦。总的来说,特征结构配置法下无人机飞控系统俯仰角能快速跟踪指令信号,横侧向运动的协调转弯控制实现了滚转角快速跟踪指令信号、无人机快速转弯以及零侧滑保持,具有较好的飞行动态性能。

