四足机器人跳跃控制规划及仿真分析*

任坤照，田春霖，陈 帅，郑 达，刘 岩

（1.西安交通大学 电气工程学院，陕西 西安710000；2.西安交通大学 电信学部，陕西 西安710000；3.西安交通大学 机械学院，陕西 西安710000）

由于四足仿生机器人具有高机动性，负载和适应能力强，可运用于物资运输、抢险救援等方面，因而具有广阔的应用前景。

四足机器人的性能主要取决于对复杂环境的适应能力，实现不同步态的规划最为关键。目前，国内外对四足机器人的Walk（慢步）、Trot（快步）等一般步态的研究都较为成熟，如Hiroshi Kimura等提出了基于各种复杂环境下的Walk步态的闭环控制系统[1]，李川等基于足端轨迹及CPG（Central Pattern Generators）网络对两种步态展开了研究[2-3]。但对于四足机器人的跳跃步态的研究较少，跳跃规划的理论仍需完善，在机械结构、运动过程中姿态调整也有待进一步改进，对其运动学、动力学的研究成为热点。在实际场景中，跳跃步态可以跨越障碍物，适应各种复杂地表，应用广泛，极大增强了四足机器人的运动性能。

本文着重对四足机器人的跳跃步态进行控制规划并通过搭建仿真平台进行验证。根据足端是否触地分阶段采取利用几何解析法进行轨迹规划。利用D-H法建立机身质心与各关节的坐标系，并基于正逆运动学对跳跃步态进行分析，求解出各阶段关节角度函数。同时，根据Lagrange法以及D'Alembert's原理对跳跃过程进行动力学分析，得到关节电机的力矩驱动函数。

通过SolidWork软件建立了全肘式四足机器人的结构模型，使用ADAMS和MATLAB软件对物理样机进行运动学联动仿真，验证了跳跃控制规划的有效性。

1 跳跃运动建模

四足机器人的设计模型如图1所示。在跳跃过程中，只研究正中面上的运动特征，对冠状面不做考虑。同时，由于在跳跃过程中前（后）两腿的运动状态相同，因此，可把四足机器人视为一维平面的多刚体系统。根据足底是否触地，将跳跃过程分为起跳相、腾空相和着地相。在足端腾空时机器人与地面不存在约束限制，即机身不受外部作用力与力矩。

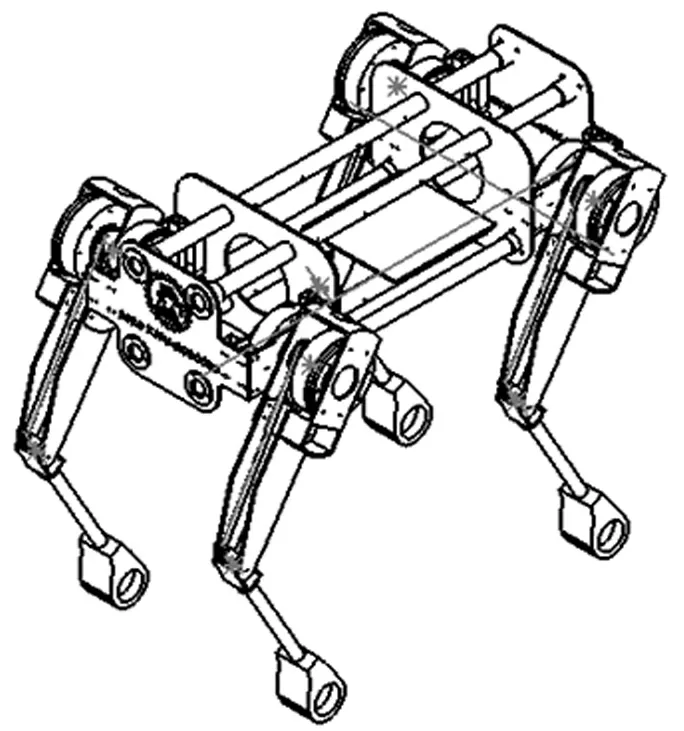
图1 四足机器人设计模型

1.1 D-H坐标系建立

如图2所示，根据D-H（）法对四足机器人建立坐标系。据此进行各坐标系的坐标转换，对跳跃过程进行运动学分析。

图2 四足机器人运动学坐标系坐标图

在躯体的几何正中心建立身体坐标系{Ob}，前进方向为x轴的正方向，竖直向上为z轴的正方向。以顺时针方向对四条腿分别编号为1，2，3，4。在每条腿的髋关节建立坐标系{Oih}（i=1，2，3，4），{Oih}的x轴正向为竖直向下方向，z轴正向为前进方向。同理，对膝关节建立坐标系{Oik}，以足端为原点建立坐标系{Oit}。由此可得身体坐标系到髋关节坐标系的转换矩阵N如式（1）。以左前腿为例，设足端运动轨迹在身体坐标系下的函数为z=f（x，y）。由足端在身体坐标系下的坐标P知足端在髋关节坐标系下的坐标P0。由此可以逆解出大小腿电机旋转角度。

式中，disx为前两腿髋关节间距；disy为同侧两腿髋关节间距。

1.2 跳跃轨迹规划

1.2.1 起跳阶段轨迹规划

起跳阶段需保证足端与接触地面有足够的摩擦力，即在跳跃过程未发生相对滑动，同时髋关节相对于足底坐标应该满足以下条件：

（1）初始机身高度为y0，水平位移为0m离地前机身高度为y1，水平位移x1；

（2）初速度为0m/s，离地前速度为v1；

（3）初加速度为0m/s2，离地前，竖直加速度为-g，水平加速度为ax1。

在起跳阶段，足底在大地坐标系下位置固定，故以足底为参考，规划机器人质心的运动方程。由于在起跳阶段，四腿同时起跳，动作一致，可只考虑单腿的运动。如图3所示，设机身质心在起跳阶段，水平加速度ax（t）=k1t，竖直加速度ay（t）=k2t（k1、k2为常系数），则水平位移为，竖直位移为

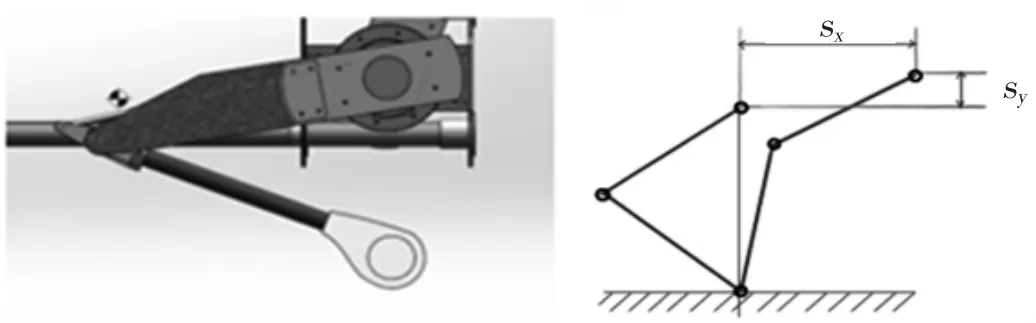
图3 跳跃阶段单腿示意图

由于髋关节的运动轨迹与质心同步，设足端为原点O，髋关节的坐标为B（PX，PY），建立如图4所示坐标系。

图4 起跳阶段腿部关节坐标系

起跳阶段D-H参数见表1。

表1 起跳阶段D-H参数

髋关节在基坐标的转换矩阵：

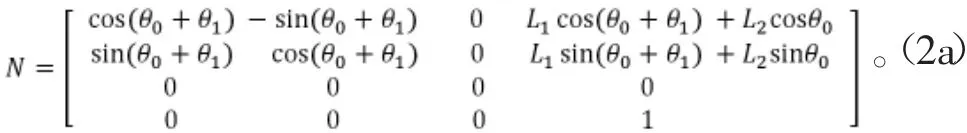
利用几何解析法对起跳阶段做逆运动学分析，由此得到关节转动角度函数：

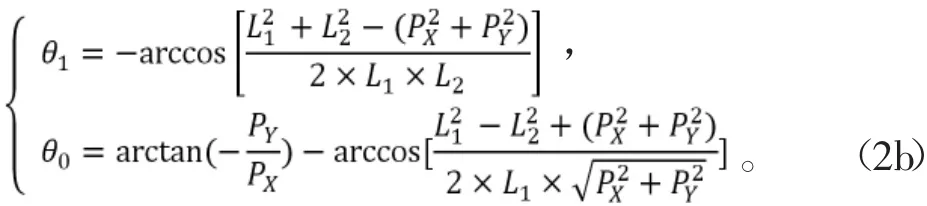
1.2.2 腾空阶段轨迹规划

足端离地后，机器人处于仅受重力作用的腾空状态。在腾空阶段机器人机身做类平抛运动，即机身在竖直方向由于以-g为加速度的匀变速运动。同时，在起跳离地时刻与着地时刻，足端与地面接触且速度均为0。在腾空阶段，在跳跃过程中足端有伸缩。

对于质心而言，跳跃阶段机身质心运动轨迹为：

式中，νx1为起跳结束时刻水平速度；νy1为竖直速度。如图5，以髋关节为原点建立坐标系：

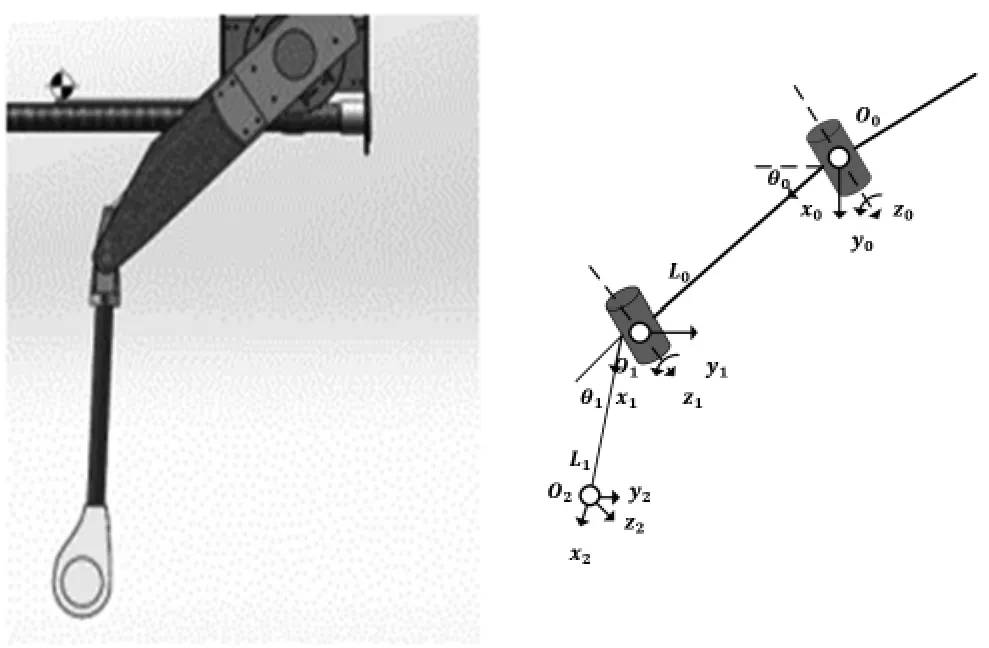
图5 腾空阶段腿部关节坐标系

足端在基坐标的转换：

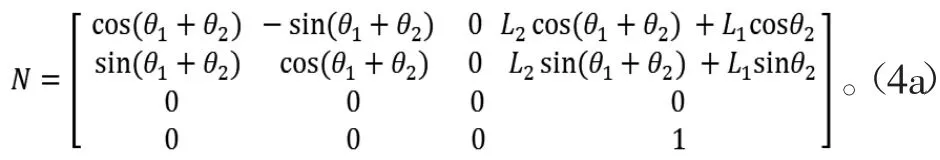
得到跳跃过程中的角度驱动函数：

跳跃机器人有一定的越障能力，欲得到跳跃跨越的最大障碍物高度极限H。用sin函数曲线以及二阶多项式拟合足端轨迹，规划足端轨迹：

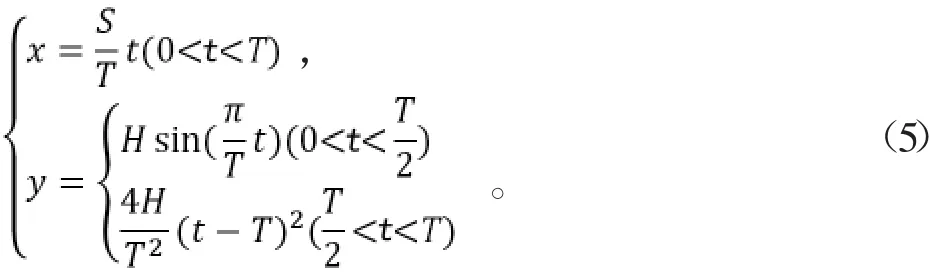
1.2.3 着地阶段轨迹规划

足端着地后，此时地面有足够的摩擦力，即无相对滑动。在电机力矩驱动下产生与机身惯性相反的作用力，使得机器人的速度减小直至为0m/s。着地阶段可视为起跳阶段的逆过程。同样，此时足端固定，如图6，建立坐标系。着地阶段质心的位移曲线为

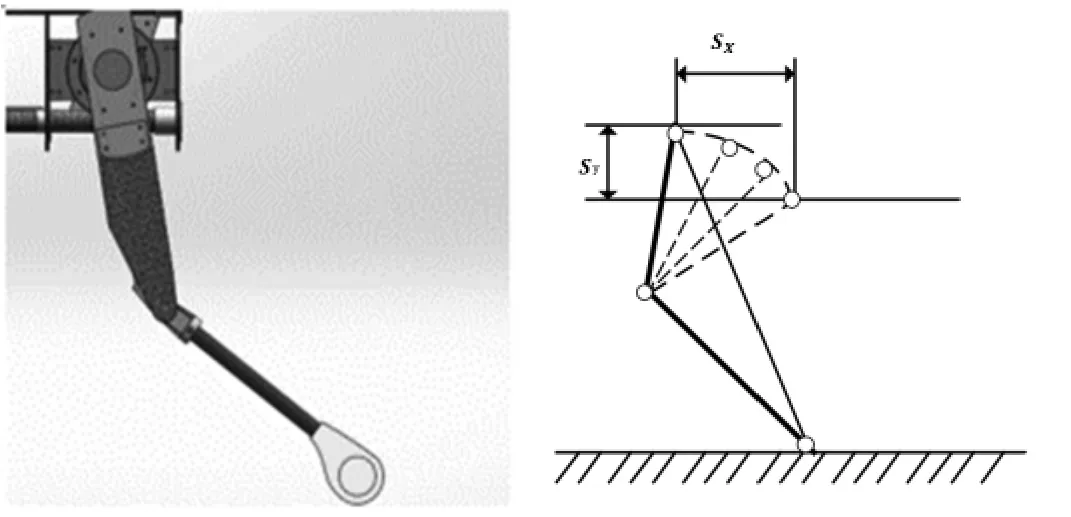
图6 着地阶段腿部关节坐标系

2 动力学建模

四足机器人关节数较多，整个系统有多个输入输出，力学关系较为复杂。本文采用Lagrange法以及D'Alembert's原理对其进行动力学分析，根据运动规划，求解跳跃过程中各关节驱动力矩，进而得到电机的驱动力函数。

力矩控制的灵敏度更高，控制方式以及动态性能更好。如图7所示，建立跳跃过程中的受力分析图：

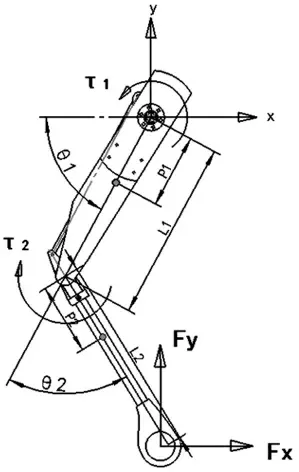
图7 四足机器人单腿的受力分析

单腿物理参数见表2。

表2 单腿物理参数

设定整个机器人的机械结构均为刚性，不发生柔性变形，同时忽略关节间的相对摩擦以及物理样机装备过程的误差。由于起跳阶段动力较为简单，此处仅讨论腾空与着地阶段的动力学分析。与运动学分析类似，建立如图7坐标系。

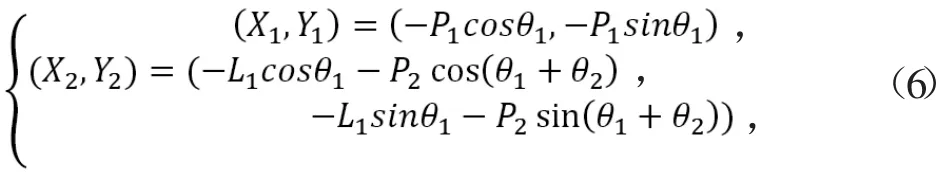
式中，P1为大腿质心到髋关节距离；P2为小腿质心到膝关节距离（X1，Y1）为大腿质心坐标；（X2，Y2）为小腿质心坐标。此时动能Ek，势能Ep为：

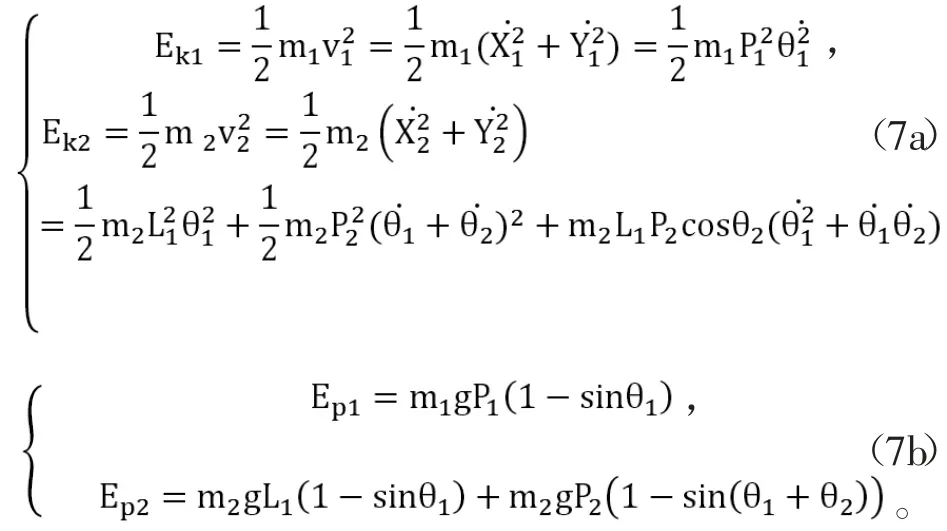
得到Lagrange函数：

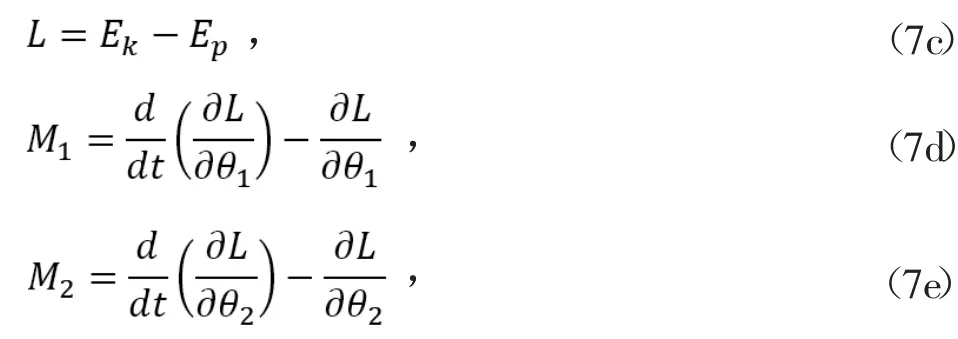
式中，M1为髋关节驱动力矩；M2为肘关节驱动力矩。

着地后，由于机身具有惯性，此时需要反方向的作用力，设此时足端与地面无相对滑动，地面给机器人的静摩擦力。根据D'Alembert's原理，对单腿力矩平衡分析得到：

如图8，对整体进行受力分析，由于跳跃过程中躯干是平动，质心处力矩为0，根据受力平衡与力矩平衡，得到式（9）的力学方程。

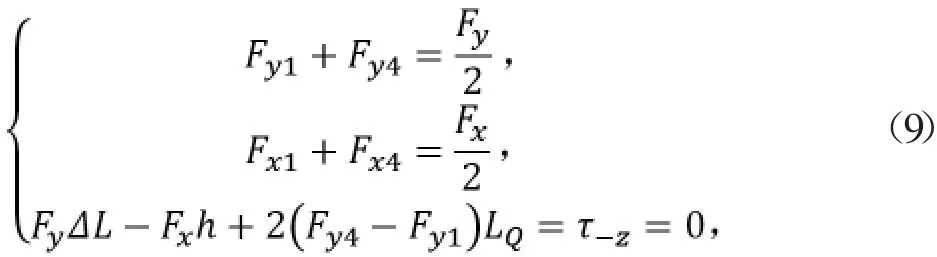
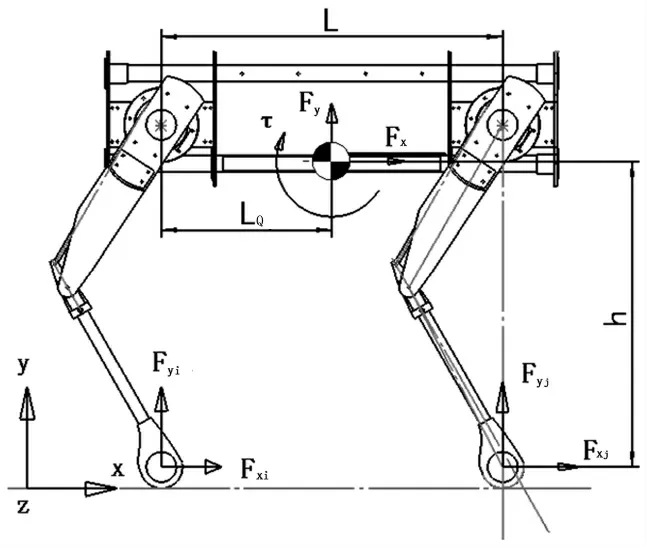
图8 四足机器人整体的受力分析

式中，Fxi、Fyi为第i条腿足端的水平与竖直方向的力，Fx Fy为质心受到的水平与竖直方向的力，LQ为质心到髋关节的水平距离。

根据轨迹规划可知大腿、小腿角加速度在开始准备跳跃的一瞬间发生突变，同时在离地和着地的瞬间有微小突变，由此引发力矩的突变。

在力矩控制中，可对这两次的突变进行一个平滑的曲线过渡，可有效减小四足机器人运动过程中受到的冲击力。

Fx1作为可变参数，结合前面驱动力矩公式得到相应驱动函数，利用MATLAB求解出如图9髋、膝关节力矩变化。由力矩图观察可得Fx1取时，即取Fx1=Fx4分析得到的力矩为最优解。

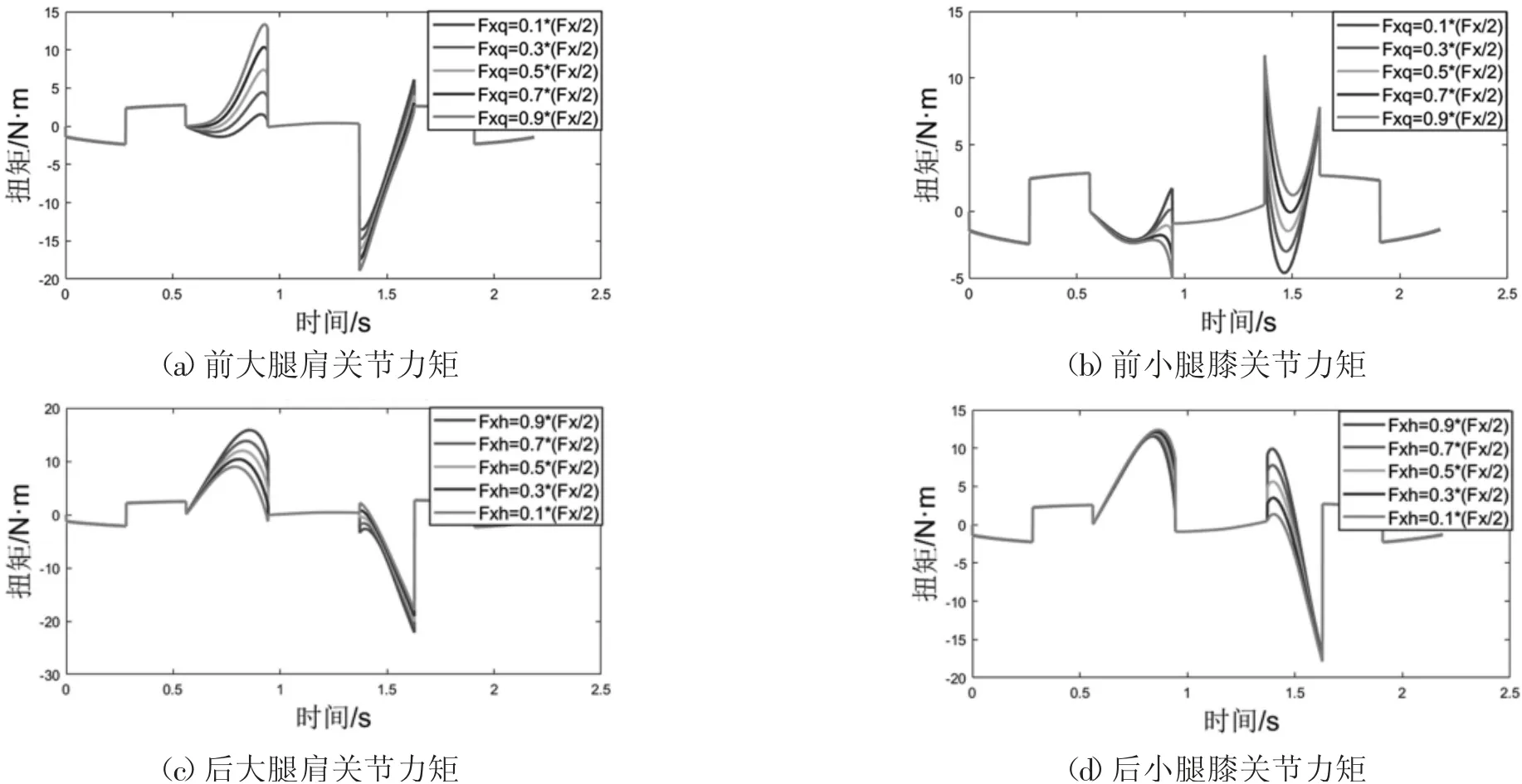
图9 髋、膝关节力矩变化曲线图

3 仿真研究

利用SolidWorks建立机器人得机械模型，并基于MATLAB中的Simulink模块搭建四足机器人系统，联合ADAMS进行模拟实际跳跃过程。

3.1 物理样机跳跃轨迹规划

根据上述的轨迹规划，对物理样机探究其跳跃阶段的最大限度。根据样机参数（如表3所示），跳跃时取每条腿的输出扭矩为T=18N·m，则跳跃时对地面的作用力为

表3 物理样机参数

设初始时，小腿与地面夹角为φ，大小腿夹角（外角）为ω，则根据规划的轨迹，加速度a在起跳过程中与时间t成线性关系，则有k1=

为了使同一腿上两个电机在起跳过程中都能以最优效率输出，应使髋关节即身体质心的运动轨迹和足端接触点与髋关节中心的角度α尽量小，故需要对起跳的姿态进行调整，而起跳的姿态主要由小腿与地面夹角φ以及大小腿夹角ω决定，通过MATLAB对φ∈（40°，70°），ω∈（130°，160°）进行迭代分析。得到：φ越大，α越小，在ω=158°时α有最小值。考虑机械结构的限制，取ω=148°。

由于φ与起跳阶段加速度及时间都有关，进而影响到跳跃的高度以及距离，为求得最优的高度与距离，通过非线性规划来得到φ的值。建立非线性规划问题：

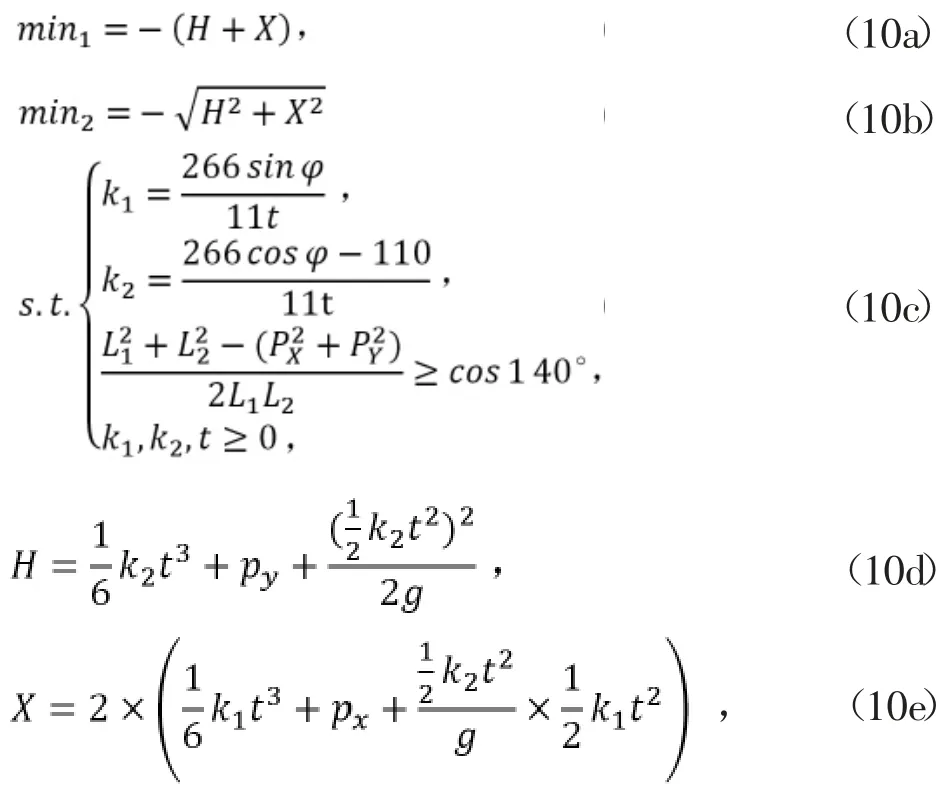
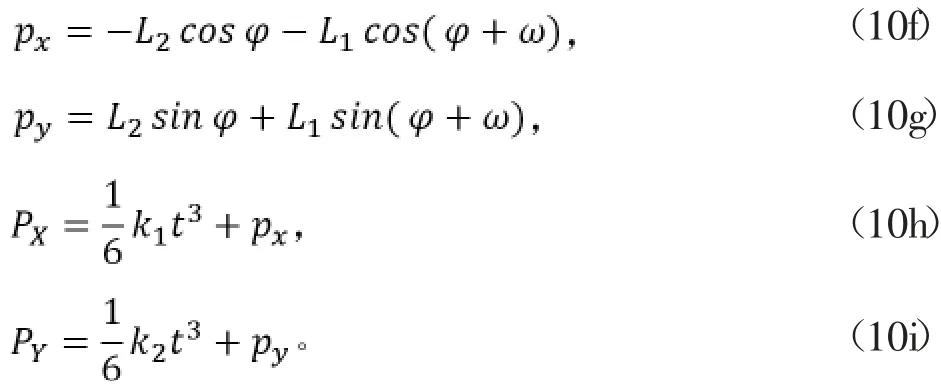
式中，（px，py）为开始起跳时髋关节较足端与地面接触点的相对位置；(PX，PY)为起跳阶段结束时髋关节相对于足端接触点的位置；H、X分别为跳跃的高度和距离。

利用MATLAB得到目标函数最优时，此时a=25.7°，t=0.384s。得到机身质心轨迹随时间变化的函数：

根据得到的质心与足端的运动轨迹函数，得到如图10的一个跳跃周期膝、髋关节角度变化曲线。

由图10可以分析得到，在起跳阶段，机体的前伸主要靠膝关节摆动，因此膝关节角度以较大幅度增加，而髋关节角度逐渐减小；在腾空期前期，膝关节的摆动对机体的竖直运动起主要作用；在跨越期间，髋关节角度变化较快，膝关节先收缩再伸展；着地后，恢复初始角度。

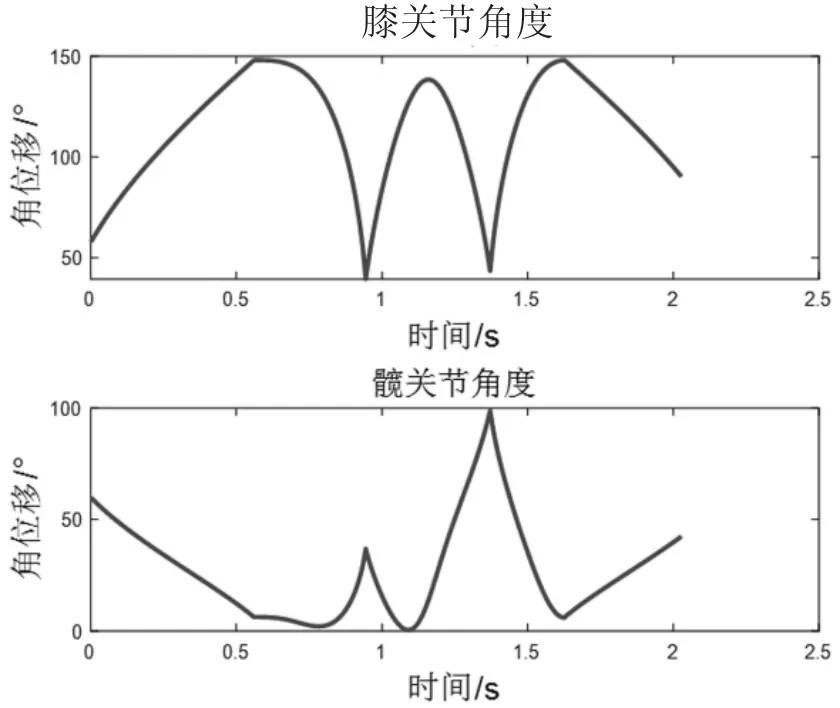
图10 膝、髋关节角位移变化曲线图

3.2 运动学仿真

通过前文规划的四足机器人在跳跃过程中的机身质心运动轨迹以及足端运动轨迹，通过正逆运动学分析，得到每条腿关节转角方程，仿真过程如图11所示。

图11 关节转角函数的运动分解图

为验证规划曲线的合理性与鲁棒性，借助ADAMS得到机身质心在水平与竖直方向位移与速度的变化图，如图12所示。

在整个跳跃周期内，通过图12可以看出整个机身在水平方向的跳跃轨迹与之前规划的运动轨迹基本一致，在某些节点处，如起跳着时的速度变化有较大起伏，最大偏差约为0.5m/s，但由于偏差时间较小，对整体运动轨迹影响较小。

图12 中质心水平方向偏移表明整个跳跃过程中机身较为稳定，但在着地的瞬间竖直方向质心会有0.005m的偏差，主要原因是在腾空阶段对身体角度的调整不够，使得下落时后脚先着地从而引起较小的偏差，可以通过加大腾空阶段的下落过程中小腿摆动角加速度，使身体下落时质心运动角度向下，机身更加平稳着地。

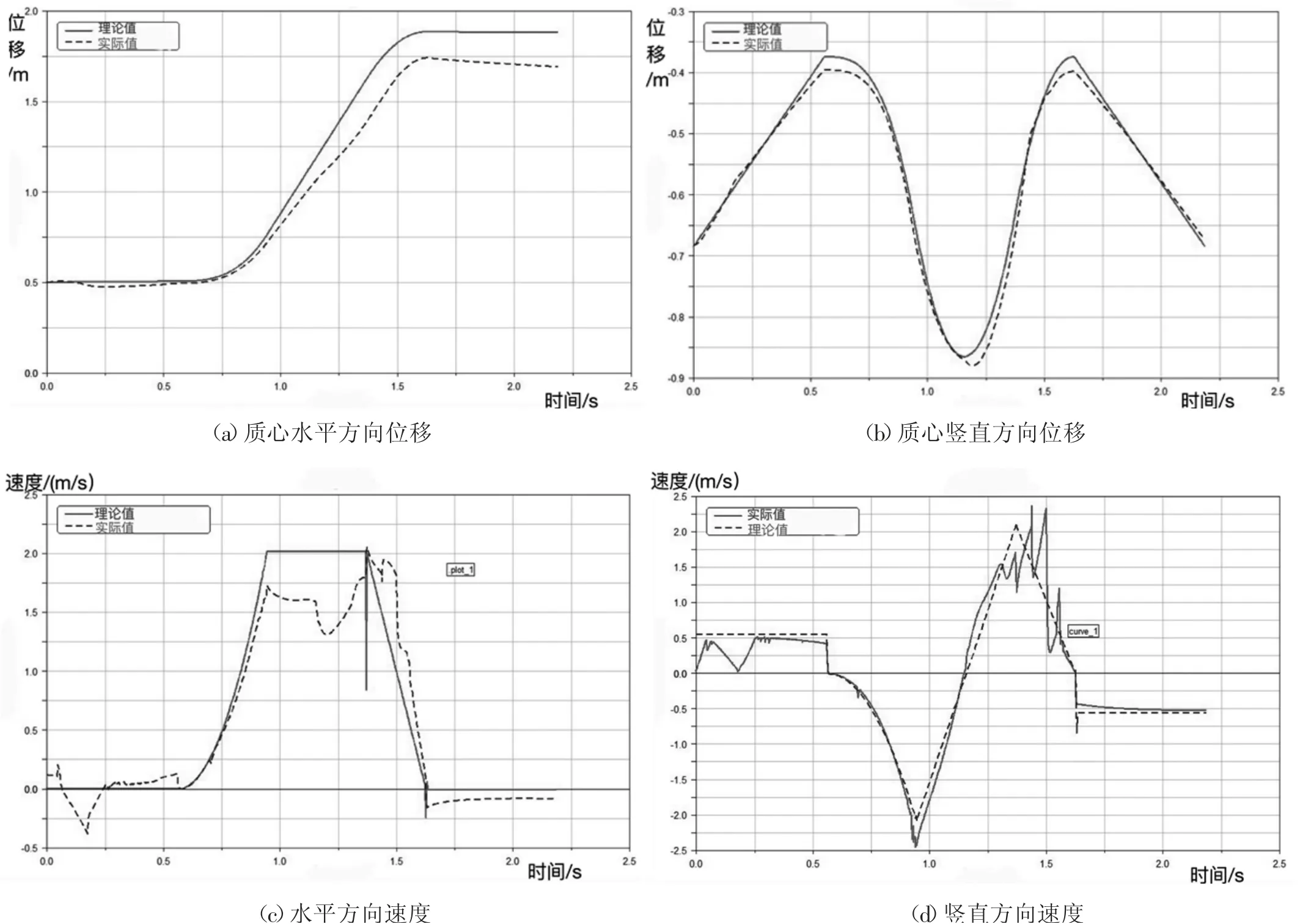
图12 跳跃过程各参数变化图

3.3 动力学仿真

整个机器人为钢体结构，与地面接触碰撞过程较为复杂，同时为验证规划的运动轨迹的正确性与合理性，故将前文得到的力矩驱动函数施加在ADAMS中对机器人模型的各腿的髋关节与肘关节，进行动力学仿真。跳跃过程，四足机器人的运动分解姿态如图13。从图13中可以看出，机身质心与足端的运动轨迹与规划的曲线基本一致。起跳阶段，获得向上以及向前的驱动力矩，肘关节变化较大，在起跳过程中起主要作用。腾空阶段，腿部有收缩，同时机身做类平抛运动。在着地阶段，机身减速，重心降低。

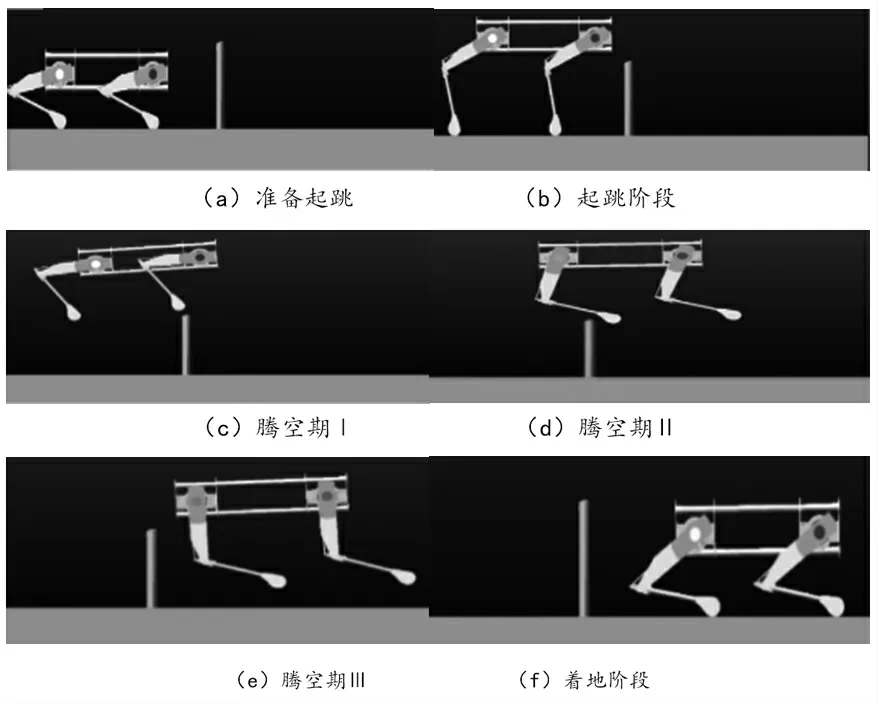
图13 关节力矩函数的运动分解图

水平与竖直方向的位移与速度的变化趋势如图14所示。在离地和着地的瞬间大小腿角加速度有微小突变，由此引发力矩的突变。可对这两次的突变进行一个平滑的曲线过渡，减小四足机器人运动过程中受到的冲击力。仿真结果与理论值基本一致，验证了前文规划曲线以及力矩驱动函数的正确性。

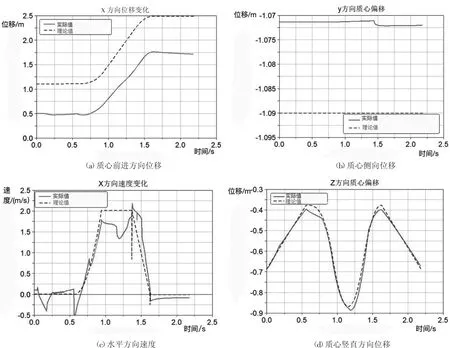
图14 跨高栏全过程控制效果图

4 结束语

根据四足动物跳跃运动特性，本文将跳跃过程分为起跳、腾空和着地三个阶段分别进行运动曲线的规划。通过正逆运动学分析得到了关节转角控制函数，并基于Lagrange法以及D'Alembert's原理进行动力学分析推导出力矩驱动控制函数。利用SolidWorks建立物理样机模型，利用ADAMS联合MATLAB搭建仿真平台。进行了物理样机的运动学、动力学仿真，将仿真结果与理论值进行比较，从而验证了跳跃运动规划曲线的可行性与正确性，以及角度控制、力矩控制的准确性与鲁棒性，为后续四足机器人或其他跳跃型机器人控制规划以及仿真实验的研究提供了基础。