硬岩矿柱变形失稳的数值模拟研究

何 川，史 默

（陕西彬长文家坡矿业有限公司，陕西 咸阳713599）

截止2019年底全国规模以上煤矿企业数量为5000多家，煤矿在垂直等多个相邻采场开挖过程中，矿柱经历了多次来压，导致其变形失稳较为严重。由于采动应力环境的复杂性，稳定性分析是井工矿面临的重要因素[1]。

当下针对这个问题，通常用到的方法为理论分析、现场测量、相似模拟、数值模拟等。理论分析方法主要是运用理论力学、弹性力学、流体力学与结构力学等理论建立模型。王万红等[2]目的是得到房柱法开采中大面积采空区的稳定性规律，利用空区激光探测系统对采空区矿柱的稳定性进行了精确地探测，通过3Dmine建立数值计算模型，采场周围矿柱中垂直应力相对较小，顶板跨度越大，则下沉量越大，推出矿柱仍具有支撑能力；叶海旺等[3]根据矿柱稳定性问题提出的物理假定模型，得到了依据虚功原理建立的以位移为未知量的功能函数，进而分析讨论摩擦效应对采场稳定性的影响力学、梁、流变等建立的模型；张晨洁等[4]根据矿柱的分布特征，制定了矿柱的回采顺序，并建立了矿房矿柱回采模型，对矿柱的回采过程进行了数值模拟分析；陈寅聪等[5]依据强度折减法，根据折减系数的不同取值对最大主应力云图、塑性区分布、位移云图等进行分析。在强度折减法的基础上进行可靠度的计算，并且根据可靠度计算结果和折减系数法计算结果，对矿柱稳定性进行分析。相似模拟试验是基于物理原型，运用物理相似理论构建相似物理模型，能准确模拟动态开挖过程中岩体的力学性能变化过程；但是相比较于相似模拟试验，数值模拟试验拥有更加直观、更加清晰的模型支撑。

采用数值分析及现场监测手段，研究了硬岩矿柱变形稳定性研究问题的讨论是关于它的变形特征以及它的变形规律。

综上所述，很多研究人员研究主要集中在某个状态下矿柱稳定性开挖下矿柱的稳定性分析。本文从两个维度去研究硬岩矿柱的稳定性问题，不仅可以从多个方面去解释稳定性取决于哪些因素，而且利用FLAC3D数值模拟的研究手段，对问题进行了更为深入的探究，使得问题的解释更加清晰明了。

1 工程概述

某矿为700多米深井，冲击矿压来压显现明显，地质构造复杂，矿区水平构造应力大，节理裂隙发育严重，矿柱失稳严重。其中针对矿柱失稳情况做以下工作，从能量原理的角度出发，应用尖点突变理论的思路探索了受前期开挖影响、非对称开采矿柱的稳定性问题，建立了其失稳的尖点突变模型，导出了其失稳的充要力学条件判据，为定量研究其失稳问题作了初步探讨。该矿的水平矿柱位于700m水平以上、厚度为15m的一个富矿水平层，其水平矿柱地质模型示意图，如图1所示。700m水平的水平矿柱为富矿资源，其上、下两部分均为大体积充填物（为功能性充填），是维护上盘和下盘围岩以及上部和下部充填物稳定的一种受力结构。随着700m左右的水平开采延伸和向下推进，开采暴露的矿柱面积日渐增加。潜在的硬岩水平矿柱失稳可能性大大增加，可能影响矿山的正常生产。采用相似模型试验、数值分析及现场监测手段，研究了阶段分层矿柱的开采扰动下围岩的变形特征、破坏模式等的变形规律。因此，即需要开展硬岩水平矿柱稳定性的相关研究，为矿山安全生产提供充分的说明意义[6]。

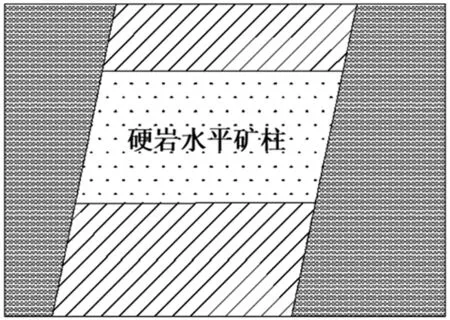
图1 硬岩水平矿柱示意图

2 硬岩矿柱稳定性分析

2.1 硬岩矿柱的本构模型

煤矿中岩石是一种天然材料，由于其生成条件、矿物成分、胶结材料以及自身结构的不同，存在许多原有的缺陷，这些原有缺陷在外界应力的作用下得到进一步的发展，才使得材料性能发生质的变化，与此同时在建立本构关系的时候应该考虑到这一因素[7]。

2.2 摩尔-库伦压缩模型

经过实验研究结果表明，可以得出岩石的摩尔-库伦压缩后的应力与位移关系有以下特性，开始加载时利用岩石的本构关系可列出以下关系[8]：

Step1：弹性阶段

Step2：压缩阶段

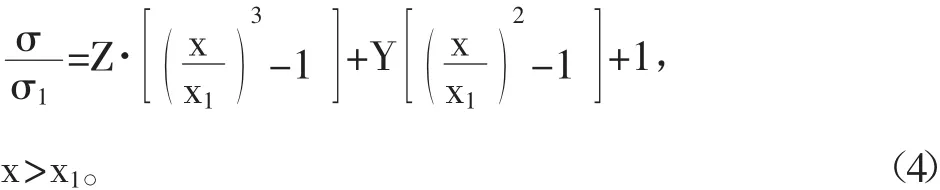
公式（3）、（4）中参数的含义，

式中，σ1、x1分别是峰值应力及对应的位移，μ是泊松比，σ2、x2分别是峰值后曲线拐点处应力以及相应的位移。

根据上述公式，通过对网格中心和外缘两个单元体的应力与位移对比，岩石中本来存在的微裂纹在应力作用下，随着载荷增加，进入线弹性变形阶段；当变形超过弹性极限时，微裂纹迅速传播，直至岩石应力达到峰值，如图2和图3所示。

图2 圆柱形网格

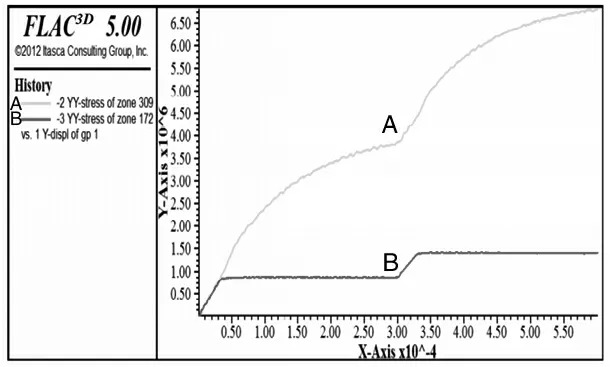
图3 摩尔-库伦压缩后的应力与位移关系曲线

2.3 应变硬化（软化）模型

通过多次实验研究结果可以得出，岩石的应变硬化（软化）模型测试关系有以下的特性，开始加载时利用岩石的本构关系可列出以下关系[9]：

步骤1：应变硬化阶段

步骤2：应变软化阶段

公式（10）、（11）中参数的含义，

式中，σ3、ε3分别是硬变应力及对应的应变，E是弹性模量，σ4、ε4分别是软化应力达到峰值时相应的应变。

通过以上阐述的公式，并结合对构建出来的正方形网格中心和外缘硬岩和软岩的应变作对比，岩石中自身存在的裂纹在应力作用下，随着载荷增加，进入线弹性变形阶段，变形超过弹性极限时，微裂纹迅速传播，到达峰值后呈现下降趋势，此模型到后期破坏行为与摩尔-库伦压缩模型差距甚大，因此对于应变硬化（软化）模型，则需要更多的数据，对每一个细节进行斟酌，变化形式如图4和图5所示。

图4 正方形网格

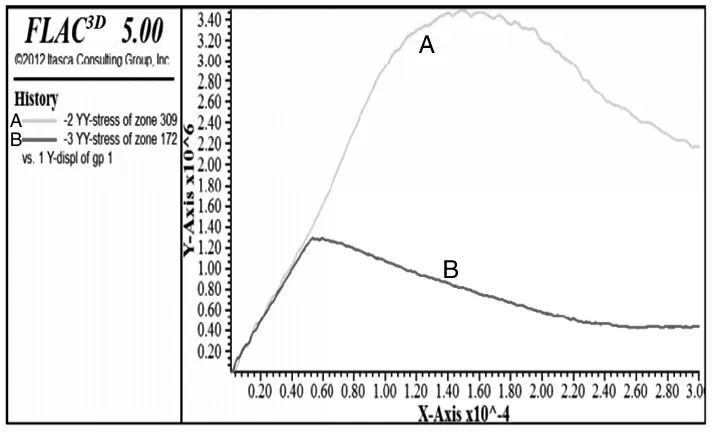
图5 应变硬化（软化）压缩后关系曲线

3 模拟结果及分析

利用FLAC3D软件对模型进行论述，根据理论分析和数值模拟的方法验证两种方式下对于硬岩矿柱的稳定性研究，得出结论：摩尔-库伦压缩模型和应变硬化和软化压缩在初期的曲线变化基本一致，在后期则出现了很大的差异，尤其是第二种方法来说，在峰值过后呈现出下降的趋势，仍然需要大量的数据进行实验，得到更为准确的关系[10]。

在现场开采采场时，留设硬岩矿柱宽度应不小于5m，隔离矿柱安全高效回采的重要保证是顶板和硬岩矿柱的稳定性，顶板稳定性的主要意义是防止冲击矿压突然出现导致硬岩矿柱的整体灾变性破坏，采场矿柱对采场顶板起着支撑作用，其稳定性直接决定着采场顶板的整体稳定性，因此一定要保证矿柱的稳定性。

对于硬岩矿柱变形稳定性问题的阐述，从两个维度解释了失稳的变化过程，虽然得出了较为准确的摩尔-库伦压缩模型在关于矿柱变形失稳方面的研究更为实用，但是仍然存在硬岩矿柱的内部因素影响，模型仍需要进一步改进。