农业机械作业大数据清洗方法与试验优化

苑严伟 徐 玲 冀福华 郭大方 安 飒 牛 康

(中国农业机械化科学研究院土壤植物机器系统技术国家重点实验室， 北京 100083)

0 引言

农机大数据平台建设是推进现代农业生产信息化、智能化、精准化的重要环节[1-7]。随着北斗系统、5G通信、物联网等技术迅速发展，大数据平台不断完善，入网农机数量猛增，数据规模不足问题得到缓解，但数据质量问题成为阻碍平台发展的新瓶颈。据统计，大型数据集中的错误率约为5%[8]。数据清洗能够减少“Garbage in, garbage out”现象，但所需时间很长，一般约占数据分析总时间的60%～80%[9-10]。准确高效的数据清洗方法能够提高平台分析决策的可靠性和时效性，是农机大数据平台发展的重要基石。

国内外关于数据清洗的研究主要集中在异常数据检测[11-17]方面，对异常数据修复的研究较少。处理异常数据的传统方式有直接保留、删除和人工填充等，其效果不够理想。ETL(Extract transform load)工具虽然能够实现数据抽取、转换和加载，但是修复能力较弱，不能满足应用需求。文献[18]针对工业大数据中的高维时间序列数据，基于领域知识支持，开发了在线与离线相结合的数据清洗系统Cleanits。文献[19]针对时间序列异常数据修复问题，提出将时间相关特性与最小变动原理相结合的IMR(Iterative minimum repairing)框架。文献[20]针对平滑过滤方法严重更改原始数据、且已有算法不支持流数据计算的问题，提出利用数据浮动速度函数修复高度异常数据的方法。文献[21-23]利用Spark分布式计算框架加快了大数据清洗流程。目前，已有数据清洗算法均未充分利用数据间的相互关系，对原始数据改动大，不适用于具有大规模、多源异构、高维度、强时空相关等特点的农机实时流数据。

为此，本文分析数据异常出现的主要场景及原因，根据农机作业数据的时间相关性和最小变动原则，提出一种数据清洗方法，依托Flink流计算平台实现数据的实时分析，通过试验验证算法的有效性，并对算法进行试验优化。

1 复杂作业条件下数据异常分析

由于应用领域存在差异，数据异常的概念缺乏统一定义。本文将数据异常定义为：在某一瞬时，服务器接收到的数据(或数据的某一部分)出现不完整、不准确、不合法等现象。

田间作业条件复杂，增加了数据异常发生的概率。在实际工作中，易发生数据异常的主要场景如下：

(1)田间环境影响传感器检测精度。例如，地块周围存在高大树木或建筑物等，会遮挡一些传感器(如卫星定位传感器)的信号，导致数据出现跳变、离散或缺失。

(2)作业工况影响传感器检测精度。例如，作业过程中土壤或谷物产生的粉尘会干扰传感器(如光学传感器)的敏感元件；地面不平整或机器运转产生的振动也会影响传感器(如冲量式测产传感器)的检测精度，导致数据出现异常。该类型数据异常具体表现为数据出现零散、漂移或抖动。

(3)农机自身因素影响传感器检测精度。例如，机器的发动机或供电系统工作不稳定，引起电压波动，导致传感器(如电容式传感器)的检测性能随电压波动。该类型数据异常具体表现为数据出现漂移、丢失或抖动。

(4)田间环境影响信息上传质量。例如，田间网络信号差或存在电磁干扰，会影响数据传送的时效性和准确性，导致数据出现延时或缺失。

本文所讨论的数据异常不包括作业环境合理变化导致的数据波动。例如：在同一地块中，由于土壤肥力不同导致农作物产量变化，尽管数据看起来比较反常，但是并不属于异常数据。

2 基于滑动窗口的数据在线清洗算法

为实现数据在线清洗，提出基于滑动窗口实现的流数据异常识别和修复算法。针对农机作业数据以数值型为主的特点，基于方差约束原则识别异常数据；基于最小变动原则，对异常数据的原始值进行初步估算，生成候选数据；根据数据时间相关性，基于AR(Autoregressive model)、ARX(Autoregressive model with exogenous input)模型得到最优修复值。因此，算法分为识别异常数据、生成候选修正数据、数据迭代修正3个步骤，如图1所示。

2.1 异常数据动态识别

在每个数据对应的窗口区间内，进行方差检验，评估其是否为异常。通过窗口的滑动，可以依次评估每个数据，实现数据流的动态异常识别。

假设原始数据集Γ内前w个数据可靠，对于Γ内第i(i=w,w+1,w+2,…)个数据γi，选取大小为w的窗口Di={di1,di2,…,diw}，其中dij=γi-w+j，则Di的方差为

(1)

式中dij—— 窗口Di中第j个数据

依据以往所采集的同类数据的方差v′，选取方差阈值v作为评判基准，v的取值应略大于v′，即v=λv′，其中λ为按经验选取的大于1的常数。当δ(Di)≤v时，则γi为正常数据；当δ(Di)>v时，则γi为异常数据。

若γi为正常数据，则窗口向后滑动，对第i+1个数据γi+1进行评估。若γi为异常数据，则修复该数据后，再向后滑动窗口。

2.2 异常数据候选修正集生成

若确定γi为异常数据，则设其为x，并令δ(Di)=v，2个原始解x1和x2求解公式为

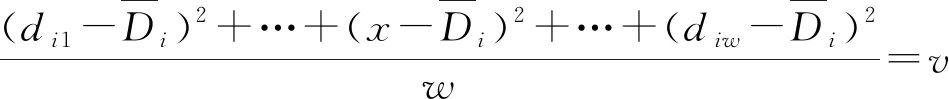
(2)

假设x1≤x2，对于异常数据γi，必然有γix2。当γix2时，γ′i取x2。候选数据γ′i，即

(3)

通过此方法，依次将所有异常数据替换为候选数据，生成候选数据集Γ′。

2.3 候选修正集迭代优化

由于生成候选数据集的方法较为粗放，因此引入AR和ARX模型，利用异常数据γi前面m个数据，对γi的候选值γ′i进行优化，保证数据修正准确可靠。

若m个数据均为正常数据，则使用AR模型更新候选数据γ′i，得到最终修复值为

(4)

C——常量m——阶数

φk——AR、ARX模型参数

εi——白噪声点

否则，使用ARX模型对第i-m个至第i-1个数据的原始值与候选值的差加权求和，更新候选数据γ′i，得到最终修复值为

(5)

其中φk、m可利用数学统计进行估算。样本数据集Γ的协方差函数符合Yule-Walker方程，可以得到

(6)

式中β0、β1、…、βp——Γ的协方差函数

转换为矩阵形式

Apφ(p)=Bp

(7)

由于矩阵Ap对称且可逆，因此可得

(8)

此时，可以求出φk，其中φ(p)的第p个分量φpp，即为偏相关函数。

根据AR(m)的特性可知，其偏自相函数m步截尾(在大于某个常数后快速趋于0)，因此可以将点(p，φpp)在笛卡尔坐标系中标出。当存在某个p之后，φpp无限接近0，此时的p即为所求的阶数m。执行迭代，直至前后2次迭代的γ′i小于阈值τ时，停止迭代。

数据异常清洗算法步骤如下：

(1)输入Γ、v、w、τ

(2)处理γi

γi→Di

ifδ(Di)≤v

else

forlto …

δ(Di)=v→x1,x2(x1≤x2)

ifγi≤x1

γ′i,0=x1

else

γ′i,0=x2

end

ifγi-m,…,γi-1do not have abnomal data

else

break

end

end

end

end

(3)输出Γ*

3 试验与分析

3.1 试验材料

在现有农机大数据平台中，选取2016—2019年某省农机深松、保护性耕作等8种类型的作业数据，规模大于1×109条，代表性字段如表1所示。

表1 农机数据基本信息

为适应农机作业数据吞吐量大、并发度高的特点，将算法迁移至大数据流计算平台Flink上，依托Flink集群的分布式特性，保证算法快速准确执行。传感器通过TCP/IP协议将海量数据传输至Kafka集群进行分组管理。然后，Flink消费者集群接收数据并运行算法，实现流数据清洗。系统部署在阿里云服务器上，相关配置如表2所示。

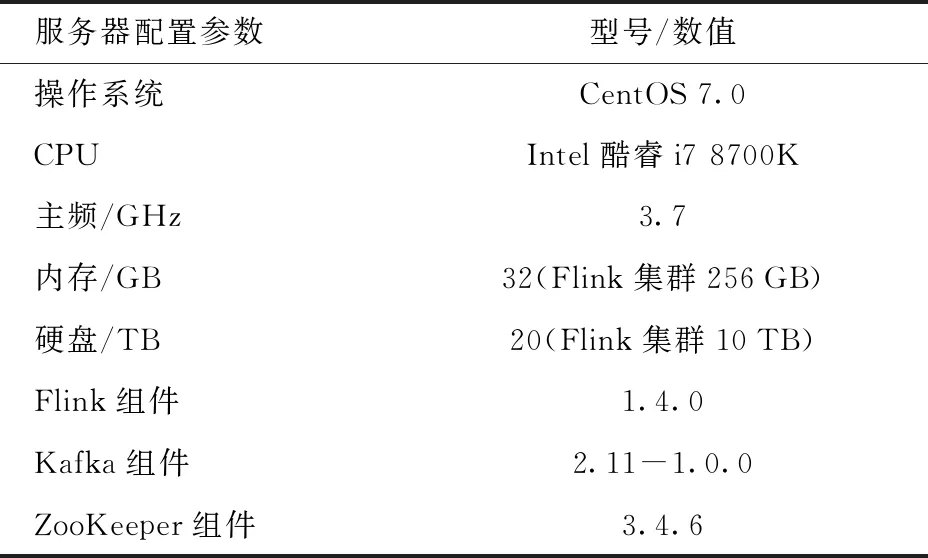
表2 试验环境

3.2 算法有效性验证

3.2.1验证方法

算法有效性包括异常数据识别有效性和修复有效性。使用精确率P1、召回率R和综合性指标F1评价异常数据识别有效性。使用均方根误差ERMSE评价数据修复有效性，计算式为

(9)

式中n——异常数据个数

算法有效性验证方案流程如图2所示。首先，选取一定规模的正常数据，并人工对其进行预处理，将一定比例的正常数据修改至异常，同时标记正常数据为1，异常数据为0。将预处理后的数据作为试验集，使用算法完成数据清洗。进行多次清洗后，取各评价指标的平均值进行分析。

为更加具体地展现本算法的修复效果，采用基于平滑的清洗算法SWAB[24]和基于否定约束的全局清洗算法Holistic[25]与本算法进行横向对比。

3.2.2验证结果

(1)选取不同规模的试验集，在数据预处理时将5%的数据修改至异常，取窗口大小为100，阶数取值为4，阈值取值为0.1。在每一规模水平下进行3次试验，分别对P1、R、F1和ERMSE取平均值。

如图3所示，P1、F1随数据量增加而增大。当数据规模达到1×105条，P1在0.94附近趋于稳定；R一直处于0.9～0.95区间内；F1大于0.92。说明算法在大规模数据集中具有较高的异常识别率。

均方根误差随数据规模的变化如图4所示。随着数据规模的增大，3种算法的均方根误差均减小，且在数据达到一定规模后，均方根误差的变化趋缓。SWAB算法均方根误差始终较高。在数据规模小于1×105条时，Holistic与本文算法表现相近，但在数据规模大于等于1×105条时，后者的均方根误差明显更小，表明本文算法修复效果较好。

(2)选取规模为1×105条的试验集，在窗口大小为100、阶数为4、阈值为0.1时，选取不同数据异常率进行试验。试验结果如图5所示，同一数据规模下，3种算法的均方根误差均随数据异常率的增大而增大，SWAB算法最高，Holistic算法次高，本文算法始终最低，说明所提出的算法在修复准确性方面有效，且数据异常率越低表现越好。

3.3 算法试验优化

由前述分析，数据规模处于较高水平、错误率处于较低水平时，二者对均方根误差的影响很小，并且实际情况中数据规模与错误率不可控。因此，对算法的优化主要考虑阶数、阈值、窗口大小对均方根误差ERMSE和算法运行时间T的影响。采用Box-Behnken原理设计试验，各试验因素编码如表3所示，试验设计与结果如表4所示，A、B、C为因素m、τ、w编码值。

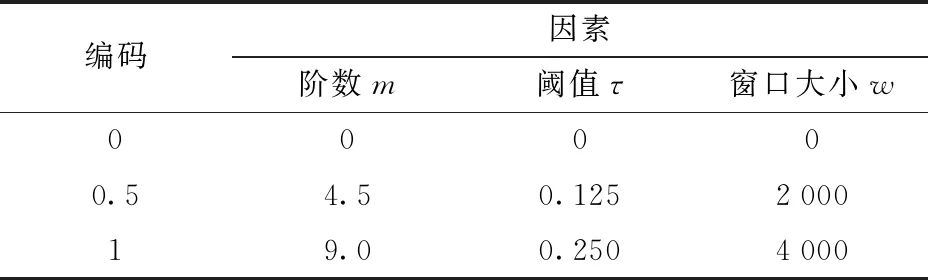
表3 因素编码

对试验结果进行分析，选择回归模型进行拟合。均方根误差和算法运行时间的方差分析结果如表5、6所示，所建立的模型均显著(P≤0.05)，且失拟项不显著，证明模型所拟合的回归方程与实际相符，能准确反映均方根误差、时间与阶数、阈值、窗口大小之间的关系。在保证模型可靠的前提下，为使回归模型更好地对试验结果进行预测，剔除不显著项，对回归模型做优化调整，分别得到ERMSE和T的回归模型为

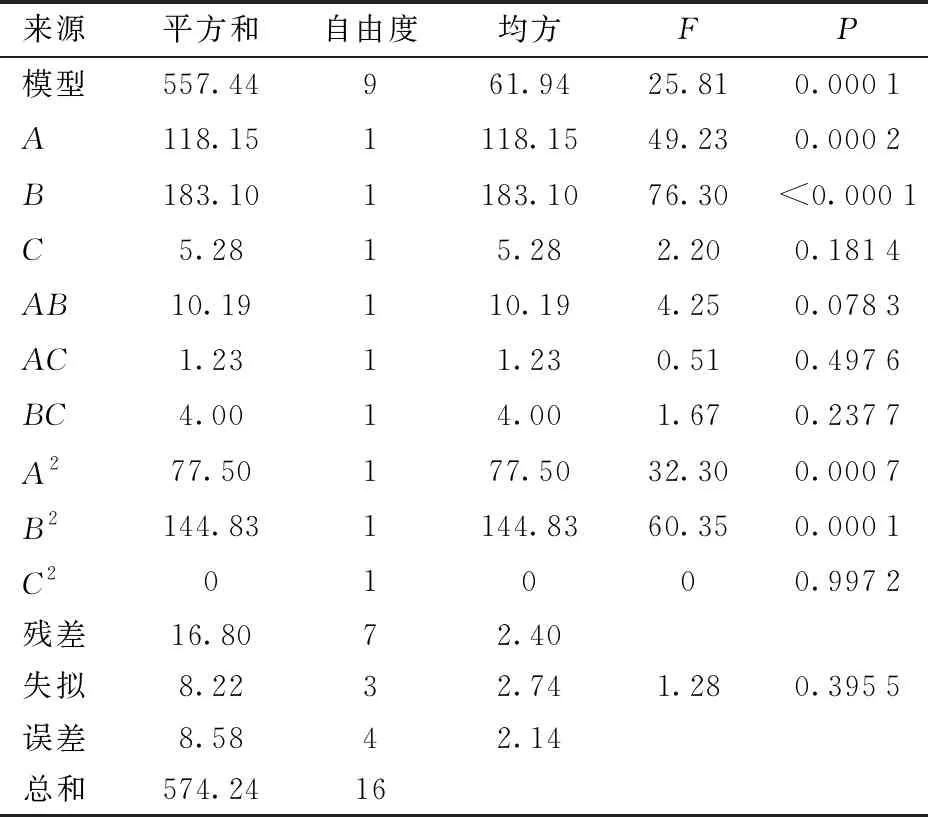
表5 均方根误差ERMSE方差分析

表6 算法运行时间T方差分析

ERMSE=11.28-24.85A-13.89B+17.16A2+23.46B2(A,B∈[0,1])

(10)

T=17.22-12.64A-38.57B+25.52A2+23.90B2(A,B∈[0,1])

(11)

将回归模型映射回原空间可得

ERMSE=11.28-2.76m-55.56τ+0.21m2+375.36τ2(m∈[0,9],τ∈[0,0.25])

(12)

T=17.22-1.4m-154.28τ+0.32m2+382.4τ2(m∈[0,9],τ∈[0,0.25])

(13)

由图6可以看出，当阈值τ一定时，随着阶数m的增大，均方根误差先减少后增大。这说明过大的阶数并不会持续增加算法的准确度。当阶数一定时，均方根误差随阈值增大而增大，这说明选取较小的阈值能提高算法准确性。

由图7可以看出，当阶数一定时，随着阈值逐渐变大，算法运行时间逐渐减少；当阈值较小时，需要较高的时间成本。当阈值一定时，算法运行时间随阶数增大而增大，结合阶数对均方根误差的影响，说明选取过大的阶数导致算法准确性差且效率低。

云服务平台使用目的不同，所要求的性能指标不同，有些注重数据准确性，有些更关注实时性。为此，本文采用二进制编码的混合遗传算法，分别对式(12)、(13)所示的模型进行优化求解，确定不同性能指标下的参数组合，优化过程如图8、9所示。设定种群个体数目为15，交叉概率为0.8，变异概率为0.08。迭代求解得到，当阶数为6.6，阈值为0.07时，均方根误差最小为0.16；当阶数为2，阈值为0.2，算法运行时间最小为0.13 s。

4 结论

(1)研究异常数据检测及修正技术，提出一种基于滑动窗口机制的数据在线清洗算法，并依托Flink分布式计算平台，加速数据的实时清洗，以适应农机大数据高并发、吞吐量大的特点。

(2)试验表明，针对规模为1×105条、异常率为5%的数据集，算法窗口大小取100、阶数取4、阈值取0.1时，精确率、召回率和综合性指标均满足数据清洗要求。与SWAB算法和Holistic算法修复后的均方根误差的对比表明，本文算法的均方根误差更小，从而证明了本文算法的有效性。本文算法的均方根误差随数据规模的增大而减小，随数据异常率的增大而增大，说明该算法适用于异常率较低的大规模数据集。

(3)基于Box-Behnken原理设计试验，分别建立均方根误差、算法运行时间与阶数、阈值、窗口大小之间的响应曲面回归模型。利用基于二进制编码的混合遗传算法求出满足各性能指标的多参数最优组合，当阶数为6.6、阈值为0.07时，均方根误差最小为0.16，当阶数为2、阈值为0.2时，算法运行时间最短为0.13 s。