以益智学具促儿童“玩”好数学

李春华

《义务教育数学课程标准（2011 年版）》（以下简称“课标”）指出，数学课程应致力于实现义务教育阶段的培养目标，要面向全体学生，适应学生个性发展的需要，使得：人人都能获得良好的数学教育，不同的人在数学上得到不同的发展。“玩”是小学生的天性，理应得到充分的理解和尊重。为了顺应学生的个性发展，笔者在教学实践中引入益智学具，确立了“玩中激趣，做中学习，悟中提升”的基本教学理念。随着教学实践的推进，学生对益智学具愈加喜欢，简直爱不释手。学生展示的机会增多，交流表达能力、动手操作能力在逐步提高，良好的数学思维品质也在逐步形成。

1.“玩”学具，激发学生的数学学习兴趣。

在数学活动课上，笔者充分利用益智学具，研发益智课程，引导学生在玩中认真观察、合理猜想、动手尝试。学生在“玩”益智学具的过程中会发现一些固定的操作步骤和数学规律，遵循这些规律就可以提升“玩”的速度，如“华容道”“汉诺塔”“神龙摆尾”等。他们饶有兴趣地在“玩”中摸索规律、记忆规律，有的学生甚至蒙上眼睛挑战“汉诺塔”学具。在这些活动过程中，学生的记忆能力和思维能力都得到了一定程度的发展与提升。

苏霍姆林斯基说过：“在儿童心灵深处，都有一种根深蒂固的需要，那就是希望自己是一个发现者、研究者、探究者。”益智课程的开展，激发了学生的发现欲望、探究欲望，拓展了他们的学习思路，突破了常规思维，他们思考问题更灵活了，数学学习兴趣也更浓厚了。

2.“做”学具，培养学生的专注学习精神。

“做中学”即让学生在动手操作的基础上进行思考，从感性的图形拼插、拼摆逐步上升到理性的思维，在动手、动口、动脑过程中不断抽象和提升，发现其中的规律，并用语言和算式表达其中的规律，感受数学的神奇之处。在一次市级公开课上，笔者执教规律探究课《斐波纳契数列的认识》。上课伊始，笔者提出要求，给定时间，让学生利用学具科学构件动手做数列的模型（如下页图1）：（1）拼出两个边长为1 厘米的正方形；（2）用两个边长为1 厘米的正方形拼成的长方形的长做边长，拼成更大的正方形，并记录边长；（3）以此类推，继续拼第3、4、5、6……个正方形，看看有什么发现。学生通过动手操作、观察思考和计算交流，借助模型和记录的边长，发现了斐波纳契数列及其排列规律（1，1，2，3，5，8，13，21，34，55，89……），第1、2 项都是1，从第3 项开始，每一项都等于相邻前两项之和。数形结合进行验证，学生又发现各个正方形的面积之和就是拼成的长方形的面积，即数列中前几项的平方和等于最后一项和下一项两个斐波那契数的乘积。在计算和观察过程中，学生又不断发现数列中前后两个数的比越来越接近黄金比。随着研究不断深入，学生不断有新发现，如奇偶项的平方规律：从第二项开始，每个奇数项的平方都比前后两项之积多1，每个偶数项的平方都比前后两项之积少1。这些也引发了学生课后持续探究的兴趣和欲望。学生在拼插和计算中表现出来的专注思考和独立探究、善于交流和质疑的精神，正是我们所期待看到的理性精神。

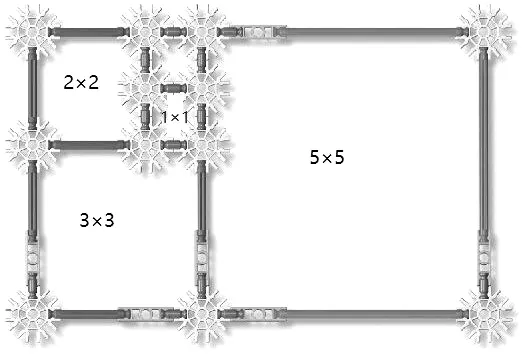
（图1）

在“做”益智学具的过程中，学生注意力高度集中，全身心投入。每做一款新学具，学生需要经历多个挫折甚至失败，这个过程更锻炼了他们坚持不懈的探究精神和专注的学习品质。同时，在对学具追根溯源的过程中，学生了解了数学的历史，受到了数学文化的熏陶。

3.“悟”学具，提升学生的数学思维品质。

数学学习需要“悟道”。课标指出，帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果。益智学具正好应和这一要求。在“玩”学具与“做”学具的过程中，学生要经历主动观察、大胆尝试、突破常规思维、及时总结、不断试错纠错等过程，直到成功破解一款学具之后，渐渐悟出一种规律，解决一类问题。我班有学生通过玩立体空间规划类学具悟到了宝石立方体的空间规划规律，再去解“木桶迷情”“圆宝石立方体”甚至更复杂的珍宝锁游戏，就轻而易举了；还有学生玩绳类学具，从简单的“魔戒大战”“哥弟双姝”入手，让绳子借助一些环、柱以及中间的一些空隙，利用化繁为简、化曲为直、转化等数学思想，在不解绳结的前提下取出戒指，再通过方法类推，从而成功解开“井底之蛙”和“困鼠游戏”等绳类学具。如此，学生后续再把悟到的经验运用到其他数学知识和其他学科知识的学习过程中，便能有效提高思维的灵活性。

综上所述，通过引导学生玩、做、悟益智学具，能有效促进学生数学思维的发展。华应龙老师曾说过：“在数学教学过程当中，把‘趣’字化为严谨的‘思’，从‘趣’入手唤起‘思’，又以‘思’升华‘趣’。”益智学具的开发利用，顺应小学生爱玩、好动的天性，使抽象的数学内容具体化、形象化、活动化，让学生在有趣的游戏中思考，在“玩转数学”的过程中领略到数学的精彩，深度体验“数学好玩”，进而积极主动地“玩好数学”。