基于复阻尼模型等效的黏性阻尼模型时域计算方法

孙攀旭，杨 红, 2，赵志明，刘庆林

(1. 重庆大学 土木工程学院， 重庆 400045； 2. 重庆大学 山地城镇建设与新技术教育部重点实验室， 重庆 400045； 3. 深圳信息职业技术学院 交通与环境学院， 广东 深圳 518172)

目前，最常用的阻尼模型是黏性阻尼模型和复阻尼模型[1].黏性阻尼模型具有数学简易性、物理上满足因果性等优点[2]，但黏性阻尼模型的计算依赖于结构振型阻尼比，结构振型阻尼比通常需要由试验测定，过程较为复杂[3].复阻尼模型直接依赖于材料的阻尼特性，不需要进行振型阻尼比的测定[4]，但具有时域发散[5]及非因果性[6]等缺陷.因此，寻找两种阻尼模型之间的等效关系，构建一种等效于复阻尼模型的黏性阻尼模型具有重要意义.

为构建等效复阻尼模型，Yang等[7]依据线弹性体的时域本构关系，采用最小二乘法使其近似等于频域内的复阻尼本构关系.Reggio等[8]采用Maxwell-Wiechert本构模型，在频域范围内近似等效于复阻尼本构模型.Wang[9]在频域内采用Rayleigh阻尼矩阵等效复阻尼矩阵.李暾等[10]基于谱矩相等原则构建出一种等效复阻尼模型，但上述方法的计算过程较为复杂.文献[3,11-12]依据复阻尼模型和黏性阻尼模型的自由振动响应，构建出损耗因子和阻尼比的近似2倍关系.在此基础上，本文以基于复阻尼模型的频率相关黏性阻尼模型[13-14]为依据，从结构固有特征恒定的角度出发，构建了材料损耗因子与结构阻尼比的更合理等效关系，进而建立了与复阻尼模型等效的黏性阻尼模型(以下简称“复阻尼等效-黏性阻尼模型”).

对于单一阻尼特性材料组成的黏性阻尼体系，阻尼矩阵满足经典阻尼条件，可直接采用实振型叠加法进行计算[15].在具体结构分析中，采用振型阻尼比构造阻尼矩阵更为直观方便[16].本文利用材料损耗因子与结构振型阻尼比的等效关系，建立了复阻尼等效-黏性阻尼模型的实振型叠加法.

对于不同阻尼特性材料组成的黏性阻尼体系，阻尼矩阵为非比例阻尼矩阵，实振型叠加法将不再适用.针对非比例阻尼体系，Clough等[15]提出可以通过构造不同阻尼比的子结构，由分块Rayleigh阻尼矩阵叠加得到非比例阻尼矩阵.在此基础上，进一步利用状态空间法实现非比例阻尼体系的复振型叠加法[17-19].但分块Rayleigh阻尼矩阵的构造依赖于子结构的振型阻尼比，子结构振型阻尼比的确定是困难的.为解决该问题，本文基于新提出的更合理的材料损耗因子与对应子结构振型阻尼比的等效关系，建立了复阻尼等效-黏性阻尼模型的复振型叠加法.

1 损耗因子与阻尼比的等效关系

1.1 复阻尼模型与黏性阻尼模型等效

基于复阻尼模型的单自由度体系时域运动方程为

(1)

式(1)对应的自由振动方程为

(2)

求解式(2)，剔除发散项[21]，可得到对应的自由振动响应为

x(t)=e-λHt(A1sinωHt+A2cosωHt)

(3)

式中：

(4)

基于黏性阻尼模型的单自由度体系时域运动方程为

(5)

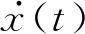
式(5)对应的自由振动方程为

(6)

求解式(6)可得

x(t)=e-λVt(C1sinωVt+C2cosωVt)

(7)

式中：

(8)

ωV为结构的有阻尼自振频率；λV为自由振动的衰减系数；C1和C2为待定系数，可由初值条件确定.

为构建阻尼比与损耗因子的等效关系，依据结构的固有特征恒定，将复阻尼模型与黏性阻尼模型的自由振动响应等效[3,11-12]，自由振动响应的等效不仅包括衰减系数的等效，还包括有阻尼自由振动频率的等效，即

λV=λH

(9)

ωV=ωH

(10)

进一步得

式(11)和(12)无法同时成立，表明复阻尼模型与黏性阻尼模型的自由振动响应是无法直接等效的.究其原因，复阻尼模型的自由振动解需要舍弃发散解，在数学上是非完整解，对应的有阻尼自振频率和衰减系数均随着损耗因子的增大而增大.而黏性阻尼模型的有阻尼自振频率随着阻尼比的增大而减小，衰减系数随着阻尼比的增大而增大.因此，理论上复阻尼模型和黏性阻尼模型的自由振动响应是不能等效的.

1.2 频率相关黏性阻尼模型与黏性阻尼模型等效

为克服复阻尼模型的时域发散缺陷，依据时频域转换原则可得到基于复阻尼模型的频率相关黏性阻尼模型[13-14]，对应的时域运动方程为

(13)

式中：ϖ为结构的振动频率.

式(13)对应的自由振动方程为

(14)

求解式(14)可得

x(t)=e-λFt(B1sinωFt+B2cosωFt)

(15)

式中：

(16)

ωF为结构的有阻尼自振频率；λF为自由振动的衰减系数；B1和B2为待定系数，可由初值条件确定.

频率相关黏性阻尼模型与黏性阻尼模型等效，可得

(17)

式(17)可转化为

(18)

(19)

式(18)和(19)是相同的，可得到结构阻尼比与材料损耗因子之间的关系式为

(20)

综上，频率相关黏性阻尼模型与黏性阻尼模型的自由振动响应是可以直接等效的，据此建立的材料损耗因子与结构阻尼比的等效关系具有更合理的物理意义.

将式(20)代入式(6)，将结构有阻尼自振频率代入式(14)，此时，式(6)和(14)具有相同的数学表达式，即

(21)

式(21)为复阻尼等效-黏性阻尼模型的时域自由振动方程.

基于构建的材料损耗因子与结构阻尼比的等效关系，频率相关黏性阻尼模型和黏性阻尼模型具有相同的自由振动方程，从而保证了结构的自由振动响应和自由振动耗散能量是相同的.

频率相关黏性阻尼模型克服了复阻尼模型的时域发散缺陷，但与复阻尼模型的频响函数相同，仍具有物理上非因果性的缺陷，同时阻尼项中包含结构振动频率的未知项，计算过程较为复杂.新建立的复阻尼等效-黏性阻尼模型可克服复阻尼模型时域发散、非因果性的缺陷，同时保留了复阻尼模型直接依赖材料损耗因子的便捷性和黏性阻尼模型的数学简易性，且材料损耗因子与结构阻尼比的等效关系也更合理.

损耗因子较小时，可作如下近似

(22)

式(20)可进一步近似为

(23)

式(23)表明，当损耗因子较小时，损耗因子与阻尼比是近似的2倍关系，与文献[3,11-12,22-23]中小阻尼比情况下损耗因子与阻尼比的关系是一致的.

在此基础上，对损耗因子近似为2倍阻尼比的适用范围进行分析，相对误差可表示为

(24)

以5%的相对误差作为界定依据，式(24)可进一步转化为

(25)

求解式(25)，可得

η≤0.580 8

(26)

综上，当η≤0.580 8时，损耗因子和2倍阻尼比的相对误差小于5%，可近似认为损耗因子与阻尼比服从2倍关系.

2 单一阻尼特性材料组成的比例阻尼 体系

基于黏性阻尼模型的多自由度体系运动方程为

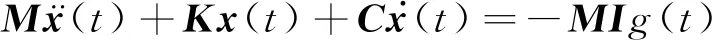
(27)

式(27)对应的无阻尼振型向量

(28)

x(t)可由振型向量线性表达：

(29)

单一阻尼特性材料的比例阻尼体系可直接采用实振型叠加法，将式(29)代入式(27)，可得

(30)

n=1,2,…,N

式中：ξn为第n阶振型对应的振型阻尼比；ωn为第n阶振型对应的无阻尼自振频率；γn为第n阶振型对应的振型参与系数，满足

(31)

材料的损耗因子在一宽泛的频率范围内是近似不变的[4]，因此单一材料结构的振型阻尼比在一宽泛频率范围内是近似不变的.通过试验可直接测得材料的损耗因子，进一步由式(20)可得到振型阻尼比为

(32)

将式(32)代入式(30)，可得到xn(t).由式(29)可得到x(t)，进而完成了式(27)的求解，即实现了复阻尼等效-黏性阻尼模型的实振型叠加法，可方便地计算由单一阻尼特性材料组成的比例阻尼体系的动力响应.

3 不同阻尼特性材料组成的非比例阻 尼体系

对于混合结构而言，无法直接利用材料损耗因子得到整体结构的振型阻尼比.只能依赖于材料损耗因子得到相应子结构对应的振型阻尼比.由式(20)可得

(33)

式中：ξj,n为第j种材料对应子结构第n阶振型的振型阻尼比；ηj为第j种材料的损耗因子.

依据子结构的振型阻尼比，需要进一步依赖于Rayleigh阻尼模型，采用分块Rayleigh阻尼模型构建结构的阻尼矩阵

(34)

式中：S为材料的种类数目；Mj为第j种材料对应的子结构质量矩阵；Kj为第j种材料对应的子结构刚度矩阵；αj和βj为对应的Rayleigh阻尼系数.

选择结构的两阶重要振型，式(34)可进一步转化为

(35)

式中：ωm为第m阶振型的无阻尼自振频率；ξj,m、ξj,n第j种材料对应子结构第m阶、第n阶振型的振型阻尼比.

求解式(35)，可得到Rayleigh阻尼系数，进而得到结构的阻尼矩阵，但通常情况下，结构的阻尼矩阵是非比例的，无法直接采用实振型叠加法.结构运动方程可等价为

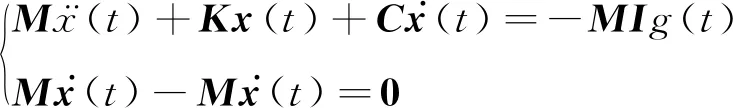
(36)

式(36)可进一步表示为

(37)

式中：

式(37)对应的复特征值为

(38)

i=1,2,…,N

式中：σi为第i阶振型的衰减系数；ωdi为第i阶振型的有阻尼自振频率.

对应于2N个复特征值的复特征向量为

(39)

令

(40)

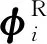
由式(38)、(40)可得

(41)

位移向量x(t)可由复特征向量线性表示

(42)

利用复特征向量的正交性，可得

(43)

(44)

4 算例分析

4.1 算例1

如图1所示，以4自由度体系为例，其具体参数取值见表1，各楼层的材料阻尼特性相同，从而构建了由单一阻尼特性材料组成的算例模型A，材料的损耗因子为0.60.模型A的初始状态为静止状态，分别采用基于复阻尼模型的频域计算方法(FFZ)和本文提出的复阻尼等效-黏性阻尼模型实振型叠加法(EVR)计算El Centro波和Taft波作用下模型A的动力响应，结果如图2、3所示.图中：t为时间，d为位移，a为加速度.其中，基于复阻尼模型的频域计算方法剔除了方程中的发散项，计算结果可视为精确解[24].不同方法计算的模型A顶层动力响应峰值对比如表2所示.

表1 模型A参数Tab.1 Parameters of Model A

表2 模型A动力响应Tab.2 Dynamic responses of Model A

图1 模型A示意图
Fig.1 Schematic diagram of Model A

El Centro波作用下，EVR和FFZ的位移时程响应近似相等，均在t=3.48 s达到位移峰值(图2(a))，位移峰值的相对误差为8.55%.EVR和FFZ的加速度时程响应近似相等，EVR在t=11.96 s处达到加速度峰值，FFZ在t=12.00 s处达到加速度峰值(图2(b))，加速度峰值的相对误差为9.46%.Taft波作用下，EVR和FFZ的位移时程响应近似相等，EVR在t=4.22 s处达到位移峰值，FFZ在t=4.24 s处达到位移峰值(图3(a))，位移峰值的相对误差为3.44%.EVR和FFZ的加速度时程响应近似相等，均在t=4.22 s处达到加速度峰值(图3(b))，加速度峰值的相对误差为6.02%.因此，EVR和FFZ的计算结果近似相等，证明了等效于复阻尼模型的黏性阻尼模型实振型叠加法的正确性.

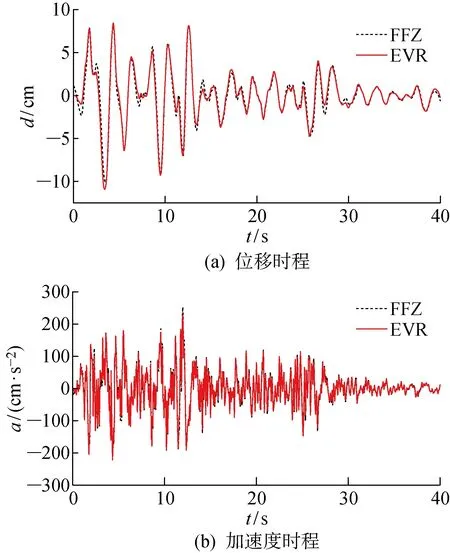
图2 El Centro波作用下模型A顶层响应Fig.2 Top floor responses of Model A in El Centro wave

图3 Taft波作用下模型A顶层响应Fig.3 Top floor responses of Model A in Taft wave

4.2 算例2

如图4所示，以2自由度体系为例，其具体参数取值见表3.第1层和第2层选择不同阻尼特性的材料，进而构建由不同阻尼特性材料组成的模型B，

图4 模型B示意图Fig.4 Schematic diagram of Model B

表3 模型B参数Tab.3 Parameters of Model B

其中，第1层、第2层材料的损耗因子分别为0.70、0.40.

依据第一阶振型和第二阶振型，可得到模型B对应的分块Rayleigh阻尼矩阵为

(46)

模型B的初始状态为静止状态，分别采用FFZ和本文提出的复阻尼等效-黏性阻尼模型复振型叠加法(EVC)计算El Centro波和Taft波作用下模型B的动力响应，结果如图5、6所示.不同方法计算的模型B顶层动力响应峰值对比如表4所示.

表4 模型B动力响应Tab.4 Dynamic responses of Model B

El Centro波作用下，EVC和FFZ的位移时程响应近似相等，EVC在t=12.30 s处达到位移峰值，FFZ在t=12.32 s处达到位移峰值(图5(a))，位移峰值的相对误差为3.82%.EVC和FFZ的加速度时程响应近似相等，均在t=11.76 s达到加速度峰值(图5(b))，加速度峰值的相对误差为8.54%.Taft波作用下，EVC和FFZ的位移时程响应近似相等，EVC在t=4.02 s处达到位移峰值，FFZ在t=4.04 s处达到位移峰值(图6(a))，位移峰值的相对误差为4.15%.EVC和FFZ的加速度时程响应近似相等，均在t=9.84 s处达到加速度峰值(图6(b))，加速度峰值的相对误差为9.68%.因此，EVC和FFZ的计算结果近似相等，证明了复阻尼等效-黏性阻尼模型复振型叠加法的正确性.

图6 Taft地震波作用下模型B顶层响应Fig.6 Top floor responses of Model B in Taft wave

5 结论

(1) 从结构固有特征恒定的角度出发，基于复阻尼模型的频率相关黏性阻尼模型，建立了材料损耗因子与结构振型阻尼比的合理等效关系.

(2) 依据材料损耗因子与结构振型阻尼比的等效关系，提出了与复阻尼模型等效的黏性阻尼模型，可克服复阻尼模型时域发散、非因果性的缺陷，同时保留了复阻尼模型直接依赖材料损耗因子的便捷性以及黏性阻尼模型的数学简易性.

(3) 对于由单一阻尼特性材料组成的比例阻尼体系，利用材料损耗因子与结构振型阻尼比相等的特征，建立了与复阻尼模型等效的黏性阻尼模型实振型叠加法.对于由不同阻尼特性材料组成的非比例阻尼体系，利用不同材料的损耗因子与对应子结构的振型阻尼比相等特征，提出了与复阻尼模型等效的黏性阻尼模型复振型叠加法，算例分析验证了两种方法的正确性.