长三角地区冬季霾污染日数的季节预测
董莹 尹志聪 段明铿


摘要 将霾日数年际增量作为预测对象、前期外强迫因子作为自变量,分别运用多元线性回归方法和广义相加模型建立长三角地区冬季霾日数预测模型。综合考察“去一法”交叉验证和循环独立样本实验的结果,选出适用于各个模型较优的建模方法,并对比长三角地区冬季霾日数预测模型(MODEL1)和长三角地区冬季霾日数分月预测模型(MODEL2)。MODEL1、MODEL2的均方根誤差(解释方差)分别为2.69(80.01%)、2.76(79.04%),两类模型均能成功捕捉霾日数的年际-年代际趋势和极值。MODEL2预测的霾日数距平同号率(97.3%)优于MODEL1(86.49%),具有良好的距平符号捕捉能力。MODEL1采用11月之前的外强迫因子,可提前一个季度预测冬季霾日数;MODEL2采用更新的外强迫因子,可不断预测每月霾污染状况。通过两类模型组合使用,可更准确预测长三角地区冬季霾日数,为霾污染治理提供可靠的科技支撑。
关键词 霾污染;年际增量;多元线性回归;广义相加模型;短期气候预测
近年来,在我国的一些地区,霾天气发生较为频繁(高歌,2008;王博妮等,2016;郑龙飞等,2016;包云轩等,2018)。霾天气使大气能见度恶化,影响公共交通安全,危害人体健康(Stanhill and Cohen,2001;白志鹏等,2006;张保安和钱公望,2007)。城市化和工业化的迅猛发展使得长三角地区成为我国受霾天气影响最严重的地区之一(Yin and Wang,2017a;尹志聪等,2019),而冬季是霾污染最严重的季节(符传博,2016)。因此研究长三角地区冬季霾日数的预报方法有着重要的现实意义。
中国东部霾日数的变化是由经济社会分量和气候变化分量相叠加而形成的(Zhang et al.,2018)。在污染物排放量大且缓慢变化的条件下,大气中的细颗粒容易达到饱和水平,气候条件成为霾形成的另一个关键因素(Yin and Wang,2016a)。同期大气环流对霾天气的形成有很大影响。冬季中国东部上空的反气旋环流可以导致更稳定的大气环境,从而为长三角地区冬季霾的形成创造更为有利的条件。合适的相对湿度促进了雾和雾霾混合向霾转换,从而导致霾日数增多(丁一汇和柳艳菊,2014;吴丹等,2016)。东亚冬季风减弱会导致偏北风的输送和水平扩散能力减弱,污染物容易堆积,为霾天气的形成创造了良好的条件(吴萍等,2016)。长三角地区显著的表面风速负异常,不利于霾扩散,从而加重了长三角地区冬季霾污染(曹建秋和郭品文,2016;吴丹等,2016;吴萍等,2016)。边界层高度降低,导致污染物浓度不断增大,有利于长三角地区霾天气的形成(花艳等,2017)。
由于东亚季风系统区气候具有准两年振荡特点,Wang et al.(2000)提出年际增量季节预测方法。某年的年际增量被定义为当年的变量值和去年的变量值之差。年际增量方法利用到前一年的观测值,从而可以较好地捕捉气候变量的年际和年代际变化(王会军等,2008,2012),同时使得预测对象信号增强,振幅变为原来振幅的2倍左右,有利于提高预测技巧。该方法曾成功应用于长江中下游夏季降水,在1997—2006年夏季降水后报中显示了较高的预测能力(Fan et al.,2008);范可等(2008)将该方法用于华北汛期降水的季节预报,显著提高了华北汛期降水的预测水平;Yin et al.(2016b)应用年际增量方法预测华北地区冬季霾日数,可以再现2010年后华北地区霾日数迅速增长的趋势,并对长三角地区冬季逐月霾日数进行预测(尹志聪等,2019),但对相关机理并没有深入阐述。因此有必要找寻与长三角地区冬季霾污染相联系的影响因子,并尝试解释这些因子造成长三角地区霾污染的影响机理,从而更好地预测长三角地区冬季的霾日数,为长三角地区霾污染治理提供合理的科技支撑。
1 资料和方法
月平均大气数据(表面大气温度数据,表面风速数据,相对湿度数据等)来自美国国家环境预测中心/美国国家大气研究中心(NCEP/NCAR)全球再分析数据集(Kalnay et al.,1996)。月平均重建海表面温度(Sea Surface Temperature,SST)数据来自美国国家海洋和大气管理局(NOAA)(Smith et al.,2008)。海冰面积数据来自Hadley中心(Rayner et al.,2003)。月平均格点土壤湿度数据来自NOAA的气候预测中心(van den Dool et al.,2003)。月平均雪盖数据来自罗格斯大学全球雪盖实验室(Robinson et al.,1993)。本文的霾日数是根据气象学定义计算得来(Yin et al.,2017)。霾定义为能见度低于10 km(2014年之后低于7.5 km)且相对湿度低于90%,一天中任意一个时次发生了霾这天就称为一个霾日数。再将沙尘等影响能见度的天气现象从霾日数中剔除,得到最终的霾日数。
在本研究中,统计模型是基于多元线性回归和广义相加模型(Yin and Wang,2017b)建立的。多元线性回归是一种模型驱动方法,预测量最终被表示为误差最小的K个预测因子的线性组合(Wilks,2011)。广义相加模型是从多元线性回归和广义线性模型发展而来的,是一种数据驱动方法(Chiang,2007)。基本原理是首先检查数据结构,为每个预测因子选择合适的平滑函数(s)。这种方法在处理预测因子和预测量之间复杂的非线性和非单调的关系时尤其有效,预测表达式由未指定的平滑函数代替。考虑到长三角地区冬季霾日数预测的实质性需求,本文分别运用这两种方法建立长三角地区冬季霾日数预测模型以及长三角地区冬季霾日数分月预测模型。通过“去一法”交叉验证(即每次建模去掉一年,用其他36 a的霾日数年际增量数据建模预测去掉的那一年,这样循环建模37次可以得到37 a交叉检验的预测结果)和循环独立样本实验的结果(对冬季霾日数和12月霾日数来说,在不同的截止年份下,采用1980至该年的霾日数年际增量数据建立预测模型预测之后到2017年的霾日数年际增量。对1月和2月的霾日数来说,在不同的截止年份下,采用1981至该年的霾日数年际增量数据建立预测模型预测之后到2018年的霾日数年际增量。)为每个模型选择最优的建模方法,并在此基础上建立两类长三角地区冬季霾日数预测模型。
2 长三角地区冬季霾日数预测模型
南极附近(0°~145°E,70°~88°S)前期7月和8月平均表面气温年际增量(xw1)增加以及印度半岛东北部(80°~83°E,19°~27°N)前期7月土壤湿度年际增量(xw5)减少会导致长三角地区表面风速减小,不利于霾扩散(表1)。新西兰东部南太平洋(140°~160°W,30°~42°S)前期6月表面气温年际增量(xw2)增加可以在中国东部925 hPa上诱导出东北风使得西南急流减弱,并向南移动,这不利于长三角地区水汽的输送,从而产生更多的霾日数。里海西北部(35°~50°E,50°~54°N)前期秋季雪盖面积年际增量(xw3)增加可以加强长三角地区上空的正位势异常,限制污染粒子的垂直运动和垂直扩散(Yin and Wang,2018)。非洲西北部(3°~10°W,19°~23°N)前期6月和7月平均土壤湿度年际增量(xw4)增加会使长三角地区相对湿度减小,有利于霾的形成。新西兰东南部(136°~158°W,44°~58°S)前期8月海表面温度年际增量(xw6)减少也可以影响到长三角地区上空的反气旋,进而影响长三角地区霾的扩散条件(表1)。上述6个影响因子和长三角地区冬季霾日数年际增量之间的相关系数分别为0.50、0.52、0.49、0.38、-0.51、-0.46,均通过置信度为95%显著性检验(表1)。
在6个预测因子中两两进行相关性分析,一共15种组合方式,其中只有一对显著相关,因此使用多元线性回归方法建模时,不存在多重共线性的问题。采用多元线性回归方法建立的长三角地区冬季霾日数季节预测模型为:fWHD=0.205 7+0.474 5xw1+1.637 0xw2+0.000 2xw3+0.043 6xw4-0.020 4xw5-1.578 4xw6。虽然预测量和预测因子之间存在显著的线性相关性,但是非线性相互作用也会影响霾日数的预测。因此,进一步建立能够涵盖非线性关系的广义相加预测模型。长三角地区冬季霾日数广义相加季节预测模型为:fWHD=0.342 3+2.531 8xw1+0.890 2s(xw2)+1.272 5s(xw3)+2.596 3xw4-2.645 2xw5-0.917 7xw6,其中fWHD为长三角地区冬季霾日数年际增量。
对两个模型进行“去一法”交叉检验,多元线性回归和广义相加模型预测的霾日数均方根误差(平均绝对误差)分别为2.69(2.05)和2.81(2.13) d,分别解释了80.01%和78.33%霾日数的总方差。多元线性回归预测的霾日数距平同号率(86.49%)略低于广义相加模型(89.19%),而其他指标表现均优于广义相加模型(表2)。通过图1可以看出多元线性回归和广义相加模型预测的冬季霾日数在大多数年份都很接近。这说明在选用了大量的预测因子之后,线性关系主导了长三角地区冬季霾日数的预测(Yin and Wang,2016b)。多元线性回归和广义相加模型预测的霾日数(年际增量)和观测霾日数(年际增量)之间的相关系数分别为0.90(0.78)和0.89(0.76),不仅能够再现霾日数的长期趋势、拐点、极值,在预报上的表现也较好,但在2016年的预测表现较差。综合考虑两种模型,选用多元线性回归方法建模预测长三角地区冬季霾日数。
为了获得更多的独立预测实验样本,进行循环独立样本实验,进一步评估该模型对霾日数的预测能力。图2a为在不同的结束年份下,多元线性回归预测模型由1980年到该年的年际增量数据建模得到,预测之后到2017年的冬季霾日数年际增量;图2b为在不同的开始年份下,多元线性回归模型由该年到2017年的年际增量数据建模得到,预测之前到1980年的冬季霾日数年际增量。通过独立样本实验可以看出,多元线性回归预测模型预测出2008—2017年霾日数距平全部为正,1980—1988年霾日数距平全部为负,预测值和观测值的距平同号率达到100%,并且每年的預测结果没有很大的变化。这表明建立的模型具有很好的稳定性(图2)。
3 长三角地区冬季霾日数分月预测模型
进一步研究发现,当线性趋势去除后,只有12月和1月霾日数之间仍然显著相关。同时3个月霾日数年际增量之间的相关性均不显著(表3)。因此尝试对长三角地区冬季3个月的霾日数分开进行预测。
3.1 长三角地区12月霾日数预测模型
地中海南部(5°~35°E,20°~30°N)前期秋季表面气温年际增量(xd1)减少和新西兰南部(148°~178°W,45°~60°S)前期6月和7月平均表面气温年际增量(xd2)减少可以加强长三角地区上空的正位势异常,限制粒子的垂直运动和垂直扩散。南极附近(40°~150°E,68°~88°S)前期8月表面气温年际增量(xd3)增加和南极附近(10°~17°E,63°~67°S)前期7月海冰面积年际增量(xd4)增加会使长三角地区表面风速减小,不利于霾的水平和垂直扩散。此外,哈得逊湾附近(80°~97°W,65°~70°N)前期6月土壤湿度年际增量(xd5)减少以及新西兰东部(140°~162°W,42°~56°S)前期8月和9月平均海表面温度年际增量(xd6)减少也可以影响到长三角地区上空的反气旋,进而影响长三角地区霾的扩散条件(表4)。上述6个影响因子和长三角地区12月霾日数年际增量之间的相关系数分别为-0.57、-0.58、0.53、0.47、-0.58、-0.52,均通过置信度为99%的显著性检验(表4)。
在6个预测因子中两两进行相关性分析,一共15种组合方式,其中只有2对显著相关,因此使用多元线性回归方法建模时,不存在多重共线性的问题。采用多元线性回归方法建立的长三角地区12月霾日数年际增量预测模型为:fDHD=0.106 7-0.201 6xd1-1.147 4xd2+0.274 3xd3+15.065 9xd4-0.016 0xd5-1.597 8xd6。考虑到非线性相互作用也会影响霾日数的预测,因此进一步建立能够涵盖非线性关系的广义相加预测模型:fDHD=0.157 7-0.865 2s(xd1)-1.387 6xd2+2.557 2xd3+3.364 1xd4-2.247 8s(xd5)-0.743 4xd6,其中fDHD为长三角地区12月霾日数年际增量。
对两个模型进行“去一法”交叉检验,多元线性回归预测的霾日数均方根误差(平均绝对误差)为1.52(1.26) d,小于广义相加模型的预测误差1.61(1.40) d;和观测霾日数的相关系数为0.81,解释了62.4%的总方差,均高于广义相加模型;预测的霾日数距平同号率(81.08%)略低于广义相加模型(83.78%)(表5)。两个模型都能够再现霾日数的长期趋势、拐点、极值,在预报上也有很高的精准度,近几年预测效果良好(图3)。多元线性回归和广义相加模型预测的12月霾日数在大多数年份都很接近。这说明在选用了大量的预测因子之后,线性关系主导了长三角地区12月霾日数的预测(Yin and Wang,2016a)。综合考虑两种模型,选用多元线性回归方法建模预测长三角地区12月霾日数。
为了获得更多的独立预测实验样本,设计循环独立样本实验,进一步评估该模型对霾日数的预测能力。实验结果表明,同号率达到100%,并且每年的预测结果较为接近。这说明建立的多元线性回归预测模型具有很好的稳定性(图4)。
3.2 长三角地区1月霾日数预测模型
印度尼西亚附近西太平洋(152°~172°E,5°S~12°N)前期秋季表面气温年际增量(xj1)增加以及南极附近(146°~154°W,62°~65°S)前期8月和9月平均海冰面积年际增量(xj4)增加可以使长三角地区的边界层高度降低,导致污染物浓度增大,从而加重了长三角地区的霾污染。智利西部南太平洋(90°~118°W,35°~45°S)前期11月表面气温年际增量(xj2)减少可以加强长三角地区上空的正位势异常,限制粒子的垂直运动和垂直扩散。所罗门群岛附近(145°~175°E,10°S~15°N)前期12月表面气温年际增量(xj3)增加、罗斯海附近(155°~164°W,66°~67°S)前期7月海冰面积年际增量(xj5)增加以及乌拉尔山附近(60°~72°E,52°~57°N)前期9月和10月平均雪盖面积年际增量(xj6)增加会导致长三角地区表面风速减小,从而不利于霾污染的扩散(表4)。上述6个影响因子和长三角地区1月霾日数年际增量之间的相关系数分别为0.58、-0.66、0.60、0.48、0.54、0.60,均通过置信度为99%显著性检验(表4)。
在6个预测因子中两两进行相关性分析,一共15种组合方式,其中只有3对显著相关,因此使用多元线性回归方法建模时,不存在多重共线性的问题。采用多元线性回归方法建立的长三角地区1月霾日数预测模型为:fJHD=0.107 0+2.703 6xj1-1.703 3xj2+0.695 6xj3+0.886xj4+13.763 6xj5-0.000 0134 6xj6。而广义相加模型为:fJHD=0.084 7+1.167 4xj1-2.093 0xj2+0.405 8s(xj3)+0.360 2s(xj4)+2.314 7xj5+0.063 7xj6,其中fJHD为长三角地区1月霾日数年际增量。
对两个模型进行“去一法”交叉检验,多元线性回归和广义相加模型预测的霾日数均方根误差(平均绝对误差)分别为1.46(1.22),1.56(1.29) d,都小于12月霾日数多元线性回归和广义相加模型预测的均方根误差(平均绝对误差)1.52(1.26)和1.61(1.40) d。多元线性回归预测的霾日数相关系数为0.84,可以解释67.31%的总方差,高于广义相加模型预测结果,而两个模型预测的霾日数距平同号率持平(83.78%)(表5)。1月霾日数的两个预测模型性能均分别优于12月霾日数的两个预测模型。通过图5可以看出多元线性回归和广义相加模型预测的1月霾日数在大多数年份都很接近。这说明在选用了大量的预测因子之后,线性关系主导了长三角地区1月霾日数的预测(Yin and Wang,2016b),两个模型都能够再现霾日数的长期趋势、拐点、极值,在预报上的表现也较好,能够预测出近几年的霾日数变化趋势。综合考虑两种模型,选用多元线性回归方法建模预测长三角地区1月霾日数。
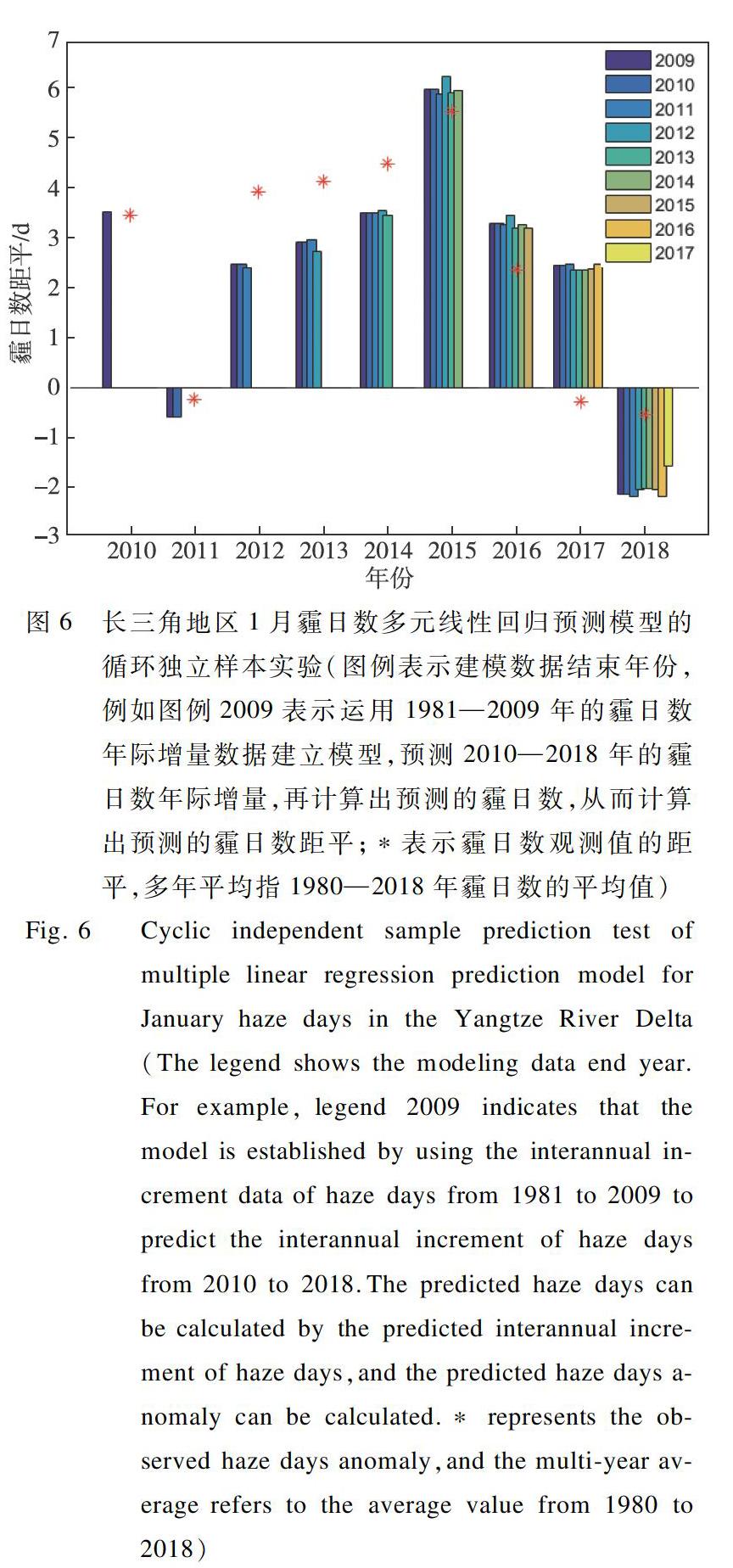
为了获得更多的独立预测实验样本,设计循环独立样本实验,进一步检验多元线性回归预测模型对霾日数的预测能力。实验结果表明,仅有2017年1月霾日数距平的符号预测错误,同号率达89.9%,并且每年的预测结果较为接近。这说明建立的多元线性回归预测模型具有很好的稳定性。但对于2017年1月的霾日数预测需要进一步的研究(图6)。
3.3 长三角地区2月霾日数预测模型
北冰洋附近(138°~175°W,73°~85°N)前期10月和11月平均表面气温年际增量(xf1)增加以及中国东部(105°~122°E,25°~35°N)前期1月表面气温年际增量(xf2)减少可以加强长三角地区上空的正位势异常,限制粒子的垂直运动和垂直扩散。斯瓦尔巴群岛附近(0°~40°E,72°~82°N)前期1月表面气温年际增量(xf3)减少会使长三角地区的相对湿度减小,有利于2月霾天气的形成。贝加尔湖附近(108°~122°E,56°~60°N)前期夏季土壤湿度年际增量(xf4)减少以及澳大利亚南部(108°~126°E,52°~64°S)前期1月海表面温度年际增量(xf6)减少也可以影响到长三角地区上空的反气旋,进而影响长三角地区霾的扩散条件。美国西北部(100°~110°W,41°~45°N)前期11月土壤湿度年际增量(xf5)减少可以减小长三角地区表面风速,不利于霾的水平和垂直扩散(表4)。上述6个影响因子和长三角地区2月霾日数年际增量之间的相关系数分别为0.50、-0.53、-0.56、-0.58、-0.55、-0.44,均通过置信度为99%显著性检验(表4)。
在6个预测因子中两两进行相关性分析,一共15种组合方式,其中只有2对显著相关,因此使用多元线性回归方法建模时,不存在多重共线性的问题。采用多元线性回归方法建立的长三角地区2月霾日数的预测模型为:fFHD=-0.008 4+0.263 7xf1-0.530 6xf2-0.112 7xf3-0.045 3xf4-0.013 1xf5-1.712 4xf6,其中fFHD为长三角地区2月霾日数年际增量。对模型进行“去一法”交叉检验,预测的霾日数均方根误差(平均绝对误差)为0.92(0.73) d,均小于1月多元线性回归预测的误差1.46(1.22) d,和观测霾日数的相关系数为0.93,能够解释86.39%的总方差,距平同号率达到83.78%(表5),能够再现霾日数的长期趋势、拐点、极值,近几年的预测效果很好(图7)。虽然预测量和预测因子之间存在线性相关性,但是非线性相互作用也会影响霾日数的预测。因此,进一步建立能够涵盖非线性关系的广义相加预测模型:fFHD=0.100 0+1.122 9xf1-1.965 1s(xf2)-0.533 7xf3-3.146 5xf4-1.209 4xf5-1.212 2xf6。对该模型进行“去一法”交叉检验,广义相加模型预测的霾日数距平同号率为89.19%,和观测霾日数的相关系数达到0.94,能够解释87.24%的总方差,均方根误差(平均绝对误差)仅0.89(0.68) d,所有指标均优于多元线性回归预测模型(表5),对近几年霾日数的预测较为准确(图7),因此选用广义相加模型預测长三角地区2月霾日数。此外,2月霾日数的两个预测模型各个指标的表现均优于1月和12月对应的霾日数预测模型。
为了获得更多的独立样本,设计循环独立样本实验,进一步评估该模型对霾日数的预测能力。实验结果表明,距平同号率达100%,且每年的预测结果较为接近。这说明建立的广义相加模型稳定性较好(图8)。
4 两类模型预测性能对比
在对长三角地区冬季霾日数整体建模(MODEL1)以及对长三角地区冬季霾日数分月建模(MODEL2)的基础上,比较这两类模型对长三角地区冬季霾日数的预测性能。
表6中两类模型的性能对比可以看出,MODEL2预测的霾日数距平同号率(97.3%)较高,对霾日数距平符号的捕捉能力较好,而MODEL1预测的霾日数均方根误差(平均绝对误差)为2.69(2.05)d均小于MODEL2预测的霾日数均方根误差(平均绝对误差)2.76(2.23)d。MODEL1和MODEL2预测的霾日数相关系数都达到0.90,能够反映出霾日数的变化趋势、拐点、极值等。MODEL1预测的2016年霾日数误差要明显大于MODEL2预测的霾日数误差,MODEL2在近年来的表现优于MODEL1(图9)。对两类模型进行循环独立样本实验,距平同号率均达到100%。这说明两类模型的稳定性均较好(图略)。
综合来看,两者的预测性能大体处于相似的水平,均方根误差约为2.5 d,对霾日数的长期变化趋势具有很好的再现能力。区别是MODEL1采用11月之前的外强迫因子,可以提前一个季度预测出冬季霾日数,而MODEL2采用了预测月份前一个月的外强迫因子,可以不断更新每月更详细的预报结论,对霾日数距平符号的捕捉能力较好。
5 结论与讨论
本文以霾日数年际增量为预测对象,分别运用多元线性回归和广义相加模型针对长三角地区冬季霾日数整体建模以及分月建模。根据“去一法”交叉检验和循环独立样本实验的结果,考察多元线性回归和广义相加模型的优劣,选出各个模型较优的建模方法,再比较两类采用较优建模方法的预测模型的预测效果。
总体来看,长三角地区冬季霾日数分月预测模型(MODEL2)預测出的霾日数距平同号率较高达到97.30%,对霾日数距平的捕捉能力较好,且近几年的预报表现要优于长三角地区冬季霾日数预测模型(MODEL1)。MODEL1只运用11月之前的外强迫因子,可以提前一个季度预测出长三角地区冬季霾日数,而MODEL2运用了预测月份前一个月的外强迫因子,可以不断更新每月的预测值,从而得到更为详细的预报结论。两类模型组合使用,可以更准确地预测长三角地区冬季霾日数。分月来看,2月霾日数预测模型的性能最好,能够解释霾日数87.24%的方差,均方根误差仅有0.89 d,平均绝对误差仅0.68 d,霾日数距平同号率达到89.19%。
尽管这两类模型均表现很好并且预测出的2017年长三角地区冬季霾日数的误差较小,但它们仍然在某些年份有较大的预测误差。一个可能的原因是一些有用的因子特别是人类活动相关的因子没有被包含进来。本文中,我们简单假设了当前年份和前一年的污染排放量之间的差异很小并且社会经济成分变化缓慢。这个假设可以支持大多数年份的霾日数季节预测,但在某些年份,污染排放量变化迅速,因此需要将社会经济分量考虑进来。
参考文献(References)
白志鹏,蔡斌彬,董海燕,等,2006.灰霾的健康效应[J].环境污染与防治,28(3):198-201. Bai Z P,Cai B B,Dong H Y,et al.,2006.Adverse health effects caused by dust haze:a review[J].Environ Pollut Control,28(3):198-201.(in Chinese).
包云轩,邵艺,李迅,2018.基于MODIS的北京一次霾过程的能见度反演[J].大气科学学报,41(5):710-719. Bao Y X,Shao Y,Li X,2018.Visibility inversion of a haze process in Beijing by remote sensing based on MODIS satellite observations[J].Trans Atmos Sci,41(5):710-719.(in Chinese).
曹剑秋,郭品文,2016.江苏省雾霾天气特征分析[J].气象科学,36(4):483-493. Cao J Q,Guo P W,2016.Characteristics analysis on fog and haze weather in Jiangsu Province[J].J Meteor Sci,36(4):483-493.(in Chinese).
Chiang A Y,2007.Generalized additive models:an introduction with R[J].Technometrics,49(3):360-361.
丁一汇,柳艳菊,2014.近50年我国雾和霾的长期变化特征及其与大气湿度的关系[J].中国科学(地球科学),44(1):37-48. Ding Y H,Liu Y J,2014.Analysis of long-term variations of fog and haze in China in recent 50 years and their relations with atmospheric humidity[J].Sci Sin Terrae,44(1):37-48.(in Chinese).
范可,林美静,高煜中,2008.用年际增量方法预测华北汛期降水[J].中国科学(地球科学),38(11):1452-1459. Fan K,Lin M J,Gao Y Z,2008[J].Sci China Ser D:Earth Sci,38(11):1452-1459.(in Chinese).
Fan K,Wang H J,Choi Y J,2008.A physically-based statistical forecast model for the middle-lower reaches of the Yangtze River Valley summer rainfall[J].Chin Sci Bull,53(4):602-609.
符传博,唐家翔,丹利,等,2016.1960—2013年我国霾污染的时空变化[J].环境科学,37(9):3237-3248. Fu C B,Tang J X,Dan L,et al.,2016.Temporal and spatialvariation of haze pollution over China from 1960 to 2013[J].Environ Sci,37(9):3237-3248.(in Chinese).
高歌,2008.1961—2005年中国霾日气候特征及变化分析[J].地理学报,63(7):761-768. Gao G,2008.The climatic characteristics and change of haze days over China during 1961—2005[J].Acta Geogr Sin,63(7):761-768.(in Chinese).
花艷,潘良宝,汤莉莉,等,2017.南京霾天颗粒物数浓度特征及其受气象条件影响分析[J].气象科学,37(3):385-393. Hua Y,Pan L B,Tang L L,et al.,2017.Characteristics of the particulate number concentration and association with meteorological conditions during winter haze episode in Nanjing[J].J Meteor Sci,37(3):385-393.(in Chinese).
Kalnay E,Kanamitsu M,Kistler R,et al.,1996.The NCEP/NCAR 40-year reanalysis project[J].Bull Amer Meteor Soc,77(3):437-471.
Rayner N A,Parker D E,Horton E B,et al.,2003.Global analyses of sea surface temperature,sea ice,and night marine air temperature since the late nineteenth century[J].J Geophys Res:Atmos,108(D14):4407.
Robinson D A,Dewey K F,Heim R R Jr,1993.Global snow cover monitoring:an update[J].Bull Amer Meteor Soc,74(9):1689-1696.
Smith T M,Reynolds R W,Peterson T C,et al.,2008.Improvements to NOAAs historical merged land-ocean surface temperature analysis(1880—2006)[J].J Climate,21(10):2283-2296.
StanhillG,Cohen S,2001.Global dimming:a review of the evidence for a wide spread and significant reduction in global radiation with discussion of its probable causes and possible agricultural consequences[J].Agric For Meteorol,107(4):255-278.
van den Dool H,Huang J,Fan Y,2003.Performance and analysis of the constructed analogue method applied to US soil moisture over 1981—2001[J].J Geophys Res:Atmos,108(D16):8617.
王博妮,濮梅娟,苗茜,2016.江苏地区连续性雾霾天气的污染物浓度变化的特征和分析[J].大气科学学报,39(2):243-252. Wang B N,Pu M J,Miao Q,2016.Analysis of the characteristics and variation of pollutant concentrations for a long-lasting fog and haze event in the Jiangsu area[J].Trans Atmos Sci,39(2):243-252.(in Chinese).
Wang H J,Zhou G Q,Zhao Y,2000.An effective method for correcting the seasonal-interannual prediction of summer climate anomaly[J].Adv Atmos Sci,17(2):234-240.
王会军,孙建奇,郎咸梅,等,2008.几年来我国气候年际变异和短期气候预测研究的一些新成果[J].大气科学,32(4):806-814. Wang H J,Sun J Q,Lang X M,et al.,2008.Some new results in the research of the interannual climate variability and short-term climate prediction[J].Chin J Atmos Sci,32(4):806-814.(in Chinese).
王会军,范可,郎咸梅,等,2012.中国短期气候预测的新理论、新方法和新技术[M].北京:气象出版社:226. Wang H J,Fan K,Lang X M,2012.New theory,method and new technology for short-term climate prediction in China[M].Beijing:China Meteorological Press:226.(in Chinese).
Wilks D S,2011.Statistical methods in the atmospheric sciences[M].Oxford:Academic Press.
吴丹,于亚鑫,夏俊荣,等,2016.南京市灰霾天气的长时间变化特征及其气候原因探讨[J].大气科学学报,39(2):232-242. Wu D,Yu Y X,Xia J R,et al.,2016.Long-term variation in haze days and related climatic factors in Nanjing[J].Trans Atmos Sci,39(2):232-242.(in Chinese).
吳萍,丁一汇,柳艳菊,等,2016.中国中东部冬季霾日的形成与东亚冬季风和大气湿度的关系[J].气象学报,74(3):352-366. Wu P,Ding Y H,Liu Y J,et al.,2016.Influence of the East Asian winter monsoon and atmospheric humidity on the winter time haze frequency over central-eastern China[J].Acta Meteorol Sin,74(3):352-366.(in Chinese).
Yin Z C,Wang H J,2016a.The relationship between the subtropical western Pacific SST and haze over North-Central North China Plain[J].Int J Climatol,36(10):3479-3491.doi:10.1002/joc.4570.
Yin Z C,Wang H J,2016b.Seasonal prediction of winter haze days in the north central North China Plain[J].Atmos Chem Phys,16(23):14843-14852.doi:10.5194/acp-16-14843-2016.
Yin Z C,Wang H J,2017a.Role of atmospheric circulations in haze pollution in December 2016[J].Atmos Chem Phys,17(18):11673-11681.doi:10.5194/acp-17-11673-2017.
Yin Z C,Wang H J,2017b.Statistical prediction of winter haze days in the North China plain using the generalized additive model[J].J Appl Meteor Climatol,56(9):2411-2419.doi:10.1175/jamc-d-17-0013.1.
Yin Z C,Wang H J,2018.The strengthening relationship between Eurasian snow cover and December haze days in central North China after the mid-1990s[J].Atmos Chem Phys,18(7):4753-4763.doi:10.5194/acp-18-4753-2018.
Yin Z C,Wang H J,Chen H,2017.Understanding severe winter haze events in the North China Plain in 2014:roles of climate anomalies[J].Atmos Chemistr Phys,17(3):1641-1651.
尹志聪,王会军,段明铿,2019.近几年我国霾污染实时季节预测概要[J].大气科学学报,42(1):2-13. Yin Z C,Wang H J,Duan M K,2019.Outline of the real-time seasonal haze pollution prediction in China in recent years[J].Trans Atmos Sci,42(1):2-13.doi:10.13878/j.cnki.dqkxxb.20181224001.(in Chinese).
张保安,钱公望,2007.中国灰霾历史渊源和现状分析[J].环境与可持续发展,32(1):56-58. Zhang B A,Qian G W,2007.Analysis on the status quo and the historical origins of the haze in China[J].Environ Sustain Dev,32(1):56-58.doi:10.19758/j.cnki.issn1673-288x.2007.01.023.(in Chinese).
Zhang Q Q,Ma Q,Zhao B,et al.,2018.Winter haze over North China Plain from 2009 to 2016:influence of emission and meteorology[J].Environ Pollut,242:1308-1318.doi:10.1016/j.envpol.2018.08.019.
郑龙飞,谢郁宁,刘强,等,2016.南京地区2013年12月重霾污染事件成因分析[J].大气科学学报,39(4):546-553. Zheng L F,Xie Y N,Liu Q,et al.,2016.Heavy haze events during December 2013 in Nanjing[J].Trans Atmos Sci,39(4):546-553.(in Chinese).
In recent years with the development of social economy,the Yangtze River Delta has experienced serious haze pollution,which has brought great harm to traffic safety,ecosystem and human health.Taking the interannual increment of haze days as the prediction object and the external forcing factors in the early stage as the independent variables,the prediction models of winter haze days in the Yangtze River Delta are established by using the multiple linear regression method and the generalized additive model.By comprehensively investigating the results of “one-year-out” cross validation and cyclic independent sample prediction test,this paper selects the optimal modeling method applicable to each model and compares the Yangtze River Delta winter haze days prediction model (MODEL1) and the Yangtze River Delta haze days prediction model in different winter months (MODEL2).Root mean square errors (explained variances) of MODEL1 and MODEL2 are 2.69 (80.01%) and 2.76 (79.04%),respectively.Both models can successfully capture the interannual and interdecadal trends and extreme values of haze days.The percentage of the same sign (meaning mathematical signs of fitted and observed haze days anomalies are same) predicted by MODEL2 (97.3%) is better than that predicted by MODEL1 (86.49%),showing that MODEL2 has better ability to capture the anomalous signs.By selecting external forcing factors before November,MODEL1 can predict winter haze days one quarter in advance.MODEL2 can constantly predict monthly haze pollution by selecting newer external forcing factors.By combining the two models,it can more accurately predict winter haze days in the Yangtze River Delta,which provides reliable scientific and technological support for the haze pollution control.
haze pollution;interannual increment;multiple linear regression;generalized additive model;short-term climate prediction
doi:10.13878/j.cnki.dqkxxb.20200525001
(責任编辑:张福颖)

