“电路”课程教学内容中变换思想探讨

王清华， 郭燕飞

(太原科技大学 电子信息工程学院，山西 太原 030024)

0 引言

习近平总书记在2019 年3月召开的学校思想政治理论课教师座谈会上指出，要坚持灌输性和启发性相统一，注重启发性教育，引导学生发现问题、分析问题、思考问题，在不断启发中让学生水到渠成得出结论。要坚持显性教育和隐性教育相统一，挖掘其他课程和教学方式中蕴含的思想政治教育资源，实现全员全程全方位育人[1]。讲话中再次强调了高等学校教育围绕立德树人的根本任务，思政课程和课程思政教学应当进行有机的结合。在专业课中开展课程思政的意义在于强调在传授课程知识的基础上引导学生将所学到的知识转化为内在的德行，注重将学生个人的发展与社会发展结合起来。因此，在理工科核心课中开展课程思政教育已经不是要不要做的问题，而是该如何做好的问题[2]。

“电路”课程是电气、自动化、电子信息、通信工程等电类专业开设的一门专业基础课程。该课程教学理论严密，逻辑性强，内容较多，涉及的知识面比较广，为后续课程提供理论支持。学生对该课程的掌握程度，直接或间接影响到后续专业课程的学习。作为电类专业的核心课程，我们不仅要传授相关的自然科学知识体系，让学生掌握并熟练运用自然科学知识、方法，还要传播自然科学发展过程中所蕴含的科学精神与人文精神，重点培养学生的辩证思维能力。中国古代许多优秀的文献中包含着丰富的哲学社会科学内容，形成了特有的思想体系，为我们认识世界、改造世界提供了重要依据。本文结合“电路”课程教学内容，古为今用将“穷则变，变则通，通则久”引入到教学过程中，帮助学生形成正确的世界观、人生观、价值观，提高道德修养和精神境界，训练变换思维能力。

习总书记在2018年5月28日中国科学院第十九次院士大会、中国工程院第十四次院士大会上的讲话中的引用了“穷则变，变则通，通则久”[3]。此外，总书记还在多个场合使用该典故。这句话出自《周易·系辞》，原文为“神农氏没，黄帝、尧、舜氏作，通其变，使民不倦，神而化之，使民宜之。易穷则变，变则通，通则久。是以自天佑之，吉无不利”。“穷”是指事物发展过程中会遇到瓶颈；“变”在宇宙运动变化中具有普遍性和永恒性；“通”则是运动变化的连续性和事物之间的关联性。天地间没有不变的事情，都在不停的发生变化，这就需要足够的变通思维。同样，在“电路”课程的教学过程中，也应注意引导学生发现问题，洞悉其变化，把握其规律，善于打破传统思维方式，借助数学方法，以“变”的思想寻求新出路。本文总结了三种与“变”有关的教学内容，在教学设计和教学过程中引导学生建立科学的思维方法。

1 相量法

正弦稳态电路是指激励和响应按正弦规律变化的电路。电力供电系统可以用正弦稳态电路作为模型。当电路中除正弦电源外所含的元件都是电阻时，求电路响应时需要进行三角函数的计算。当电路中含有储能元件时，根据电路的基本定律列写的电路方程是一组常微(积)分方程。由数学理论可知，当激励为正弦量时，上述微分方程中的电流变量的特解也一定是与激励同频率的正弦量。若电路处于稳定状态，同频率的各正弦量之间，仅存在有效值和初相位的差异和联系。此时，若求解和分析同频正弦函数所描述的电路方程，能获得正确的结果，但对于复杂的电路将显得非常繁琐。相量法是分析研究正弦电流电路稳定状态的一种简单易行的方法，它将数学理论中的复数和电路理论中的正弦量建立了一一对应关系，将正弦量变换为复数，是变换思想的体现。由欧拉公式可知，一个正弦函数可以用一对共轭的复指数函数表示。所以，我们借助复数形式可以简单地表述正弦量除频率以外的振幅和初相位两个要素。

我们以RLC串联电路为例，电路如图1所示。

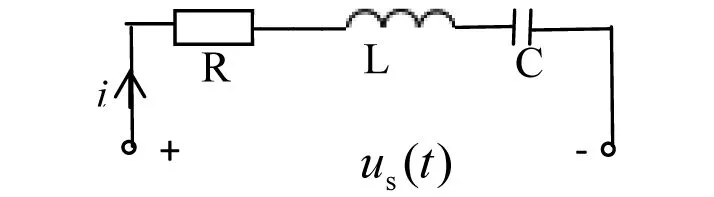
图1 RLC串联电路时域图

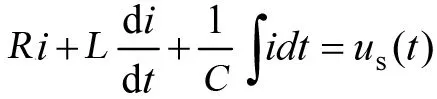
(1)

图2 RLC串联电路相量图

式(1)也可以表示为

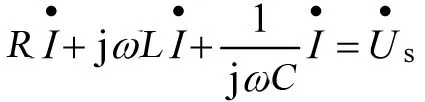
(2)

经过变换后，由式(1)的微(积)分方程变成了相量形式的代数方程(式(2))，计算则为复数运算。这样的变换在不影响电路工作状态的前提下，只在数学形式上进行了变换，将与时间有关的同频正弦函数的电路方程转换为与时间无关的复代数形式的电路方程。更加有利的是应用相量法分析正弦稳态电路时，其电路方程的相量形式与电阻电路相似[4]。因此，线性电阻电路的各种分析方法和定理可推广到线性电路的正弦稳态分析，达到了“变则通”的效果。

2 傅立叶变换

相量法是针对电源波形为正弦波时，研究了如何计算电路响应的一种变换方法。在电子、通信和信息工程中常用电压、电流作为电信号传输信息。由于单纯的正弦波并不能表现信息，还需要根据信息的不同而改变电源的振幅、相位或者频率。在脉冲波电路和逻辑电路中，需要处理脉冲波或矩形波的电压和电流。又或者当非线性设备与元件出现在电路中时，使得正弦波发生畸变。因此，当非正弦信号作用于电路时，我们需要对其进行变换，以便于分析非正弦激励下的稳态响应。非正弦信号又可以分成周期的信号和非周期的信号两类。法国数学家傅立叶提出了任何一个周期信号都可以分解为正弦和余弦信号的加权和；任何一个非周期信号都可以看成T→∞时的周期信号(T为周期)。因此，我们将傅立叶变换应用到了非正弦电流电路的稳态分析中，称为谐波分析法。

例如图3(a)中的激励电压源us(t)为一周期函数，若此函数满足狄里赫利条件，则应用数学中的傅立叶级数展开方法，将非正弦周期电压分解为一系列的频率为周期函数频率的正整数倍的正弦量之和，展开的结果是：

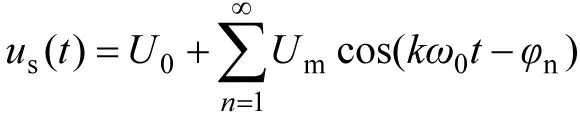
(3)

其中，U0为直流分量，基波角频率为ω0，电压us(t)可表示成直流分量与角频率为ω0,2ω0,3ω0,……的正弦波电压之和，根据线性电路的叠加原理，电压源us(t)可表示为图3(b)的电路。

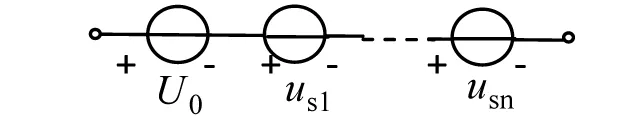
(b)分解电源图3 非正弦周期电压源及分解

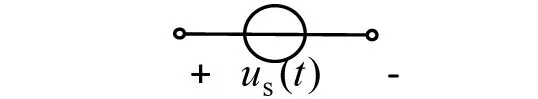
(a)非正弦周期电压源

更普遍的情况是非正弦电源或信号是非周期函数，我们可以应用傅立叶积分，得到非周期函数的变换形式。非周期函数f(t)的频谱为F(jω)，则有变换：

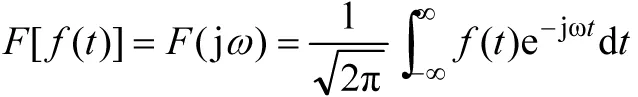
(4)

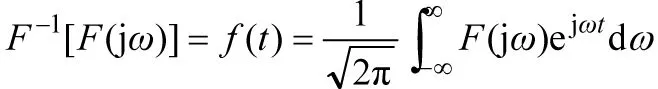
(5)

若在图1中所加的电压源us(t)为一非周期函数，在零状态条件下，设激励us(t)和响应i(t)的傅立叶变换分别为US(jω)和I(jω)，则对式(1)进行傅立叶变换得到：

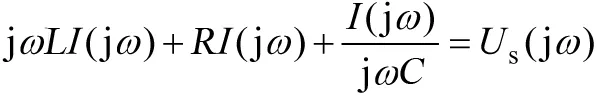
(6)

(7)

对电流I(jω)进行傅立叶反变换得到时域的响应电流i(t)为：

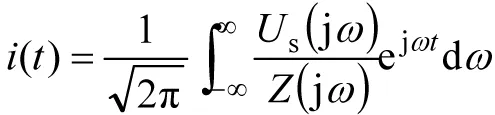
(8)

总结上述内容，在分析非正弦信号作用线性电路时，我们应用傅立叶变换将电路方程的时域的微(积)分形式“变”成了频域的代数形式，降低了分析电路的难度。经过傅立叶变换可以得到电路的频域特性，所以傅立叶变换常用于信号处理领域。

3 拉普拉斯变换

“电路”课程教学内容中，动态电路的研究是很重要的一个模块。在讲授这个内容时，我们首先采用的是经典法，即根据电路定律和元件的电压、电流关系建立描述电路的方程，而建立的方程是以时间为自变量的线性常微分方程，则求解常微分方程即可得到电路变量在时域的解。对于一阶电路和二阶电路，对应的电路方程是一阶微分方程和二阶微分方程，学生在高等数学课中已经学习了微分方程的求解方法。但遇到具有多个动态元件的复杂电路时，对应的电路方程为高阶常微分方程，此时用直接求解微分方程的方法比较困难。而且高阶常微分方程并没有固定的解法。例如要求解一个n阶的常系数线性齐次微分方程，可以运用特征根的方法求解，而非齐次的可降阶的微分方程，可以采用降阶法等等。在高等数学中，拉普拉斯变换是分析和求解常系数微分方程的简捷方法。拉普拉斯变换方法最初由19世纪末的英国工程师亥维赛(O.Heaviside, 1850-1925)应用到解决电力工程计算中。后来人们根据法国数学家拉普拉斯(P.S.Laplace, 1749-1825)的著作，对其方法进行了严格的数学论证。拉普拉斯变换也是一种积分变换，定义为：

(9)

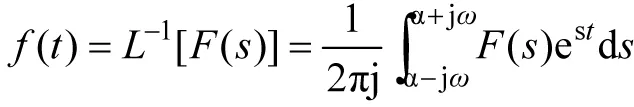
(10)

其中，F(s)为像函数，f(t)为原函数。

我们还是以RLC串联电路为例，设加在电路两端的电源为us(t)，图1为时域电路，则由基尔霍夫定律可得电路方程为式(1)。非零状态条件下，对微分方程式(1)的两端取拉普拉斯变换可得电路方程为：

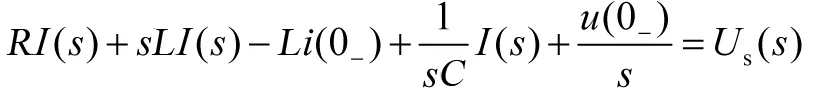
(11)

由式(11)可以看到，我们将时域的微分方程“变”为复频域的代数方程，运算电路如图4所示，由此解出像函数，再求像函数的反变换得到时域响应，这种方法简化了解题的过程，起到了“变则通”的作用，充分展现了拉普拉斯变换将给定的函数通过广义积分变为一个新的函数的意义所在。拉普拉斯变换方法也称为运算法。

图4 RLC运算电路

拉普拉斯变换方法是对连续时间系统进行分析的重要方法之一。与相量法相比较，它可以应用于更广泛的输入信号。傅里叶变换是拉普拉斯变换的特例。与拉普拉斯变换相比，傅里叶变换能更深入地了解信号的频率特性。傅里叶变换特别适用于稳态分析[5]。拉普拉斯变换更适合于包含初始条件的瞬态问题的分析。因为它允许包含初始条件，所以我们能够一次得到电路的瞬态响应和稳态响应。拉普拉斯变换的另外一大优势是引入了S域系统函数后，其零极点联系了系统的时域和频域特性，可直观的分析控制系统的运动过程，判断系统的稳定性，这在控制系统中尤为重要。

“电路”课程中的变换思维是指根据电路理论的相关知识，结合数学方法提出灵活的设想和分析。在教学过程中，教师要首先要求学生“博学”，充分的了解电路与数学的知识；然后引导学生“审问、慎思”，对于同一个问题通过变换不同的角度，另辟蹊径，培养学生的变通思维，训练学生用变换的角度去思考问题；最后启发学生“明辨、笃行”，使学生学会问题转化，将复杂工程问题转化成简单问题，将抽象问题具体化。

4 结语

“电路”课程的教学目标除了要求学生掌握电路的基础概念、基本定理外，还应培养学生科学的思辩能力、分析和解决问题的能力。本文分析了在电路基本理论教学内容中出现的一些瓶颈问题，总结了相量法、傅立叶变换、拉普拉斯变换三种变换思想在分析电路问题时的应用。引导学生学会只有具备变通的智慧，才能做到自我适应、自我反思、自我调整，培养学生在分析问题时，穷“需”变，变则通的思维能力。