考虑作业时间的区段站调车钩数分配分析

于泽涛，辛禹辰

(1.山东高速轨道交通集团有限公司 济南工程分公司，山东 济南 250101；2. 烟台职业学院 经济管理系，山东 烟台 264670)

0 引言

调车作业是铁路运输过程中必不可少的内部生产环节，其效能的发挥直接决定了铁路运输企业的效率和效益[1-2]。调车钩数是衡量调车作业量的一种单位，通常用其多少来表示调车作业量的大小。在区段站调车人员作业时间确定的情况下，预估取送调车作业中产生的调车钩数并生成合理的调车作业量分配方案，能够充分调动员工积极性，进而提高生产效率。

调车钩数的合理分配对于制订有效的调车作业计划有重要作用[3]。目前针对调车钩数的相关研究较多，如高四维等[4]提出了在调车线数量和可变条件约束下，实现统计调车钩数最优的“消逆法”理论；王雅琳等[5]提出了一种基于排序二叉树的编组钩计划自动编制方法，得到列车编组调车钩数最优数据。张博健等[6]将调移车辆数进行优化的思想融合到调车钩数最优的目标中。上述研究从不同角度直接或间接解决了调车钩数分配问题，但均未将作业时 间[7]考虑到调车钩数分配分析中。实际生产中在区段站往往使用多台调车机车处理调车作业，如果分配的调车钩数不均衡，会引起作业时间分配不均，进而影响工作效率。因此，构建基于作业时间的区段站调车钩数分配模型，以期为车站调度员合理制订调车作业计划提供有益的参考。

1 考虑作业时间的区段站调车钩数分配模型

1.1 问题描述

区段站取送调车作业是指调机从到发线出发，往相关货物线进行取、送、调移作业后，返回到发线的技术作业过程。按照实际作业内容的不同，具体的区段站货物线调车作业有取车、送车、同时送取3种作业形式。区段站为了加速车辆周转，会尽量利用本站卸空后的空车装车，存在车辆从卸车作业点移动至相应的装车作业点的调移需求[3]，因而在取车、送车和同时送取车过程中都有可能发生调移作业。

区段站往往由多台调机完成取送调车作业，为了合理分配调车作业任务，车站调度员编制调车作业计划时，需要考虑各调机对应的调车人员作业时间均衡问题，实质上就是取送调车作业过程中调车钩数均衡分配问题。综上，在考虑最长限定作业时间、发车数量、接车数量及到发线数量因素[8]的基础上，确定每一项作业的标准作业时间，求得调机每日最多可以处理的调车钩数目，可以为调车人员合理分配调车钩数，从而实现调车作业计划制订的有效性。

为了便于问题求解，结合实际做以下假设：调车车列中不存在多种车辆混和编组的情况；多台调机作业时，只能由一台调机处理调移作业；不考虑车辆因技术问题或装载超吨而产生的甩车作业。

1.2 模型建立

在区段站调车作业中，以调车钩数最优为目标，构建考虑作业时间的区段站调车钩数分配模型，具体表示为

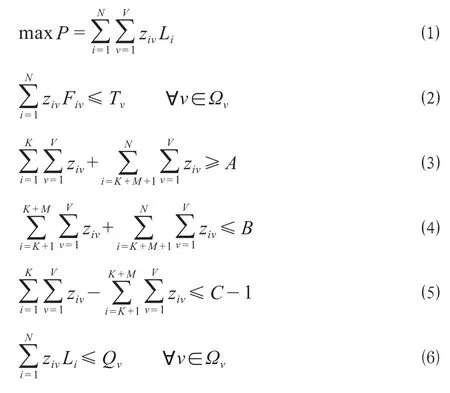
式中：P表示调车钩数量，钩；ziv表示调机v每日处理调车形式i的数量，且数量不小于0，种；Li为调车形式i包含的钩数，钩；N表示调车形式的总数，种；V表示调机的总量，辆；Fiv表示调机v处理调车形式i的标准作业时间，s；Tv表示每日调机的最长限定作业时间，s；Ωv表示调机v的集合，v= {1，2，…，V}；K表示只取不送车辆的调车形式数量，种；M表示只送不取车辆的调车形式数量，种；K + M +1表示同时送取车辆集合中第一种调车形式；A表示每日货物线已装载完成可以发出的车列数，列；B表示每日根据列车运行图统计的到达车列数，列；C表示站内到发线的数量，条；Qv表示每日调机v可处理调车钩数的最大能力，钩。ΩD表示带车辆调移的调车形式i的集合，ΩD= {W +1，…，K}∪{K + E +1，…，K + M}∪{K + M + R +1，…，N}，其中W表示不带车辆调移的只取不送调车形式数量，种；E表示不带车辆调移的只送不取调车形式数量，种；R表示不带车辆调移的同时送取调车形式数量，种。

目标函数式 ⑴ 表示调车钩数最优；公式 ⑵ 表示调机每日实际作业时间之和不超过每日调机v的最长限定作业时间；公式 ⑶ 表示只取不送和同时送取中送车列数必须满足可以发出列车列数；公式 ⑷ 表示只送不取和同时送取中送车列数不能超过到达列车列数；公式 ⑸ 表示站内到发线数量约束，且至少要有一条供调机走行的空闲到发线；公式 ⑹ 表示每台调机可处理的钩数不超过每日调机可处理的调车钩数最大能力限制；公式 ⑺ 表示多台调机同时作业时，最多由一台调机处理车辆调移作业。

1.3 模型求解

考虑作业时间的区段站调车钩数分配模型中决策变量是ziv，该变量是整数变量，因而该模型为整数规划模型，采用分支定界算法有较好的求解效率。下面对算法节点、分支过程和算法求解步骤分析如下。

（2）算法求解步骤。算法根据初始可行解作为初始下界开始分支，并以调机类型指标作为剪支规则进行剪支、迭代与优化，最终获得最优的调车钩数。算法中符号定义如下：z*为当前最优解；DB*为当前最优解的目标函数值，求得最优调车钩数目；Cn为可行节点集合，用以记录算法中经定界得到的可行节点；Cn'为分支节点集合，用以记录算法中分支得到的节点；为表示当前节点的目标函数值，即在当前节点已经统计的最优调车钩数。具体算法步骤 如下。

步骤1：初始化。根据公式(1)至公式(7)容易找出一个满足所有约束的初始解。生成根节点，将根节点放入集合Cn中，并设置当前最优解z*为该初始解，当前下界为DB*，转步骤2。

步骤2：分支。若集合Cn中无可进行分支的节点，算法结束；否则，对于集合Cn中未进行分支的节点，根据其选择的调机类型进行分支生成一组子节点，将其中各节点的父节点记录为Ovk；将节点Ovk标记为已分支，转步骤3。

步骤3：定界。对于步骤2生成的一组节点Cn'，取出其中一个节点统计得到最优调车钩数，进行以下操作：如果，转步骤4；如果，转步骤5；如果，转步骤2。

步骤4：剪支。删除按当前节点，转步骤3。

步骤5：找到可行节点。更新当前最优解z*和当前最优下界DB*；根据父节点信息生成当前最合理的调车形式统计次数；将该节点标记为已分支，并找到可行节点，将当前节点加入Cn，转步骤3。

2 算例分析

2.1 参数设置

为了验证提出的考虑作业时间的区段站调车钩数分配模型和求解算法的有效性，以山东东北部龙口港站为例，根据问题描述及模型参数设置。已知该区段站共计有6种调车形式。K = 2时，ΩK集合包含只取不送和带车辆调移的只取不送2种调车形式，分别用i = 1和i = 2表示；M = 2时，ΩM集合包含只送不取、带车辆调移的只送不取2种调车形式，分别用i = 3和i = 4表示；N = 6时，ΩS集合包含同时送取和带车辆调移的同时送取2种调车形式，分别用i = 5和i = 6表 示； W = 1，E = 1和R = 1时，ΩD集 合包含i = 2和i = 4和i = 6共3种调车形式；ΩN集合包含全部i = 1至i = 6共计6种调车形式。该区段站由2个调车组负责调车作业，并为每个调车组分别配有 1台同类型调机，因而V = 2，ΩV集合包含v = 1和 v = 2共2台调机。根据调机摘车或挂车作业的行程，可以得到不同调车形式下的调车钩数和标准作业时间如表1所示。考虑调车人员作业前准备、作业休息及调机保养等因素调机v每日最长限定作业时间T1和 T2都为30 000 s，每日货物线已装载完成可以发出的车列数A为6列，每日根据列车运行图统计的到达车列数B为6列，站内到发线的数量C为6条，每台调机最大工作能力限制Q1和Q2都为20钩。

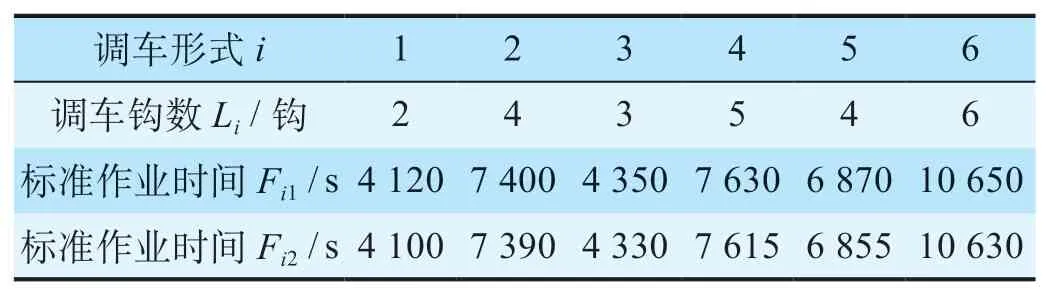
表1 调车钩数和标准作业时间Tab.1 Number of shunting hooks and standard working time

2.2 模型求解与分析

利用分支定界算法对建立的调车钩数最优单目标模型进行求解，可以求得模型目标函数值 ，即调车钩数最优为35钩，其对应的调机v处理调车形式i的数量ziv和钩数zivLi的最优方案如表2所示。

由表2分析可知，根据调机最长限定作业时间，到达车列数、发出车列数及站内到发线数等限制条件可以预估出调机v处理调车形式i的次数和钩数，方便车站调度员进行调车作业计划制订；其次调机2在调车作业中带车辆调移的调车形式共选择了3次，可以看出相较于不带车辆调移的调车形式，带车辆调移的调车形式更容易被优先选择，优先执行，这是由于带车辆调移的调车形式会更节省车辆取送过程中的走行时间，在更少的时间内完成更多钩数。另外，求得调机v处理调车形式i花费时间的最优方案如表3所示。

表2 调机v处理调车形式i的数量ziv和钩数ziv Li的最优方案Tab.2 Optimal number and hook number of shunting type i handled by shunting locomotive v

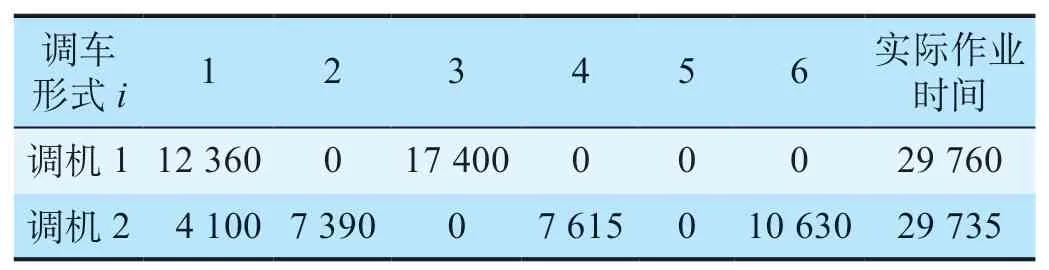
表3 调机v处理调车形式i花费时间的最优方案 sTab.3 Optimal time spent by shunting type i handled by shunting locomotive v

由表3分析可知，在区段站调车钩数统计模型中考虑作业时间可以得出调机v处理调车形式i花费的时间，在每日最长限定作业时间Tv= 30 000 s的限制下，对调车形式i进行组合选择，使调机1和调机2 的作业时间更加均衡。调机1和调机2实际作业时间与作业总时间各相差240 s和265 s，优化结果能够提高调车人员作业效率，侧面验证了考虑作业时间的区段站调车钩数分配模型的有效性。

根据模型求解结果，调机的最长限定作业时间Tv是影响调车钩数分配和调车人员积极性的重要因素，为了分析调机最长限定作业时间不同时对调车钩数和调机实际作业时间的影响，令调机最长限定作业时间在区间[25 000，35 000]中取值，间隔1 000 s， 即共分为11种情形，对算例进行敏感性分析，得到调机对应的调车钩数和实际作业时间分配结果如图1所示。

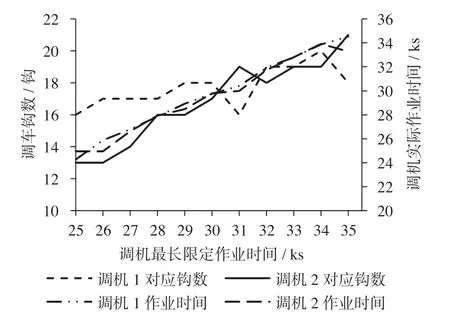
图1 调机对应的调车钩数和实际作业时间分配结果Fig.1 Number of shunting hooks and actual working time

由图1分析可知，随着调机最长限定作业时间的增多，每台调机处理的调车钩数也不断增多，调机实际作业时间也不断增加；调机1与调机2处理的调车钩数大致相同，最大相差4钩，同时可以看出每台调机对应的实际作业时间大致吻合，从而表明该模型能够为每台调机所对应的调车人员分配合适的调车作业任务，保证作业合理性。

3 结束语

调车钩数分配分析对合理制订调车作业计划有重要的现实意义。将作业时间考虑到区段站调车钩数分配模型中，能够保证在调车钩数最优的情况，兼顾调车作业公平合理，该模型验证了带车辆调移的调车形式会被优先选择，间接证明该种调车形式对提高调车作业效率有积极意义。作业时间变化会对调车钩数分配产生一定影响，不论作业时间如何变化，基于作业时间的区段站调车钩数分配模型能保证每位调车人员作业时间的均衡。在实际作业中，因车辆装载超吨、车辆技术问题及车辆混编等情况经常发生，今后应将这些因素考虑到调车钩数分配模型研究中。